К методологии проверки интегральных оценок социально-экономических объектов

Прогнозирование экономического роста, развития и социальных последствий является важной задачей для государственных структур. С помощью данного инструмента они могут предсказать последствия планируемых действий и в соответствии с этим в правильном направлении скорректировать свою деятельность и политику, чтобы избежать серьезных социальноэкономических потрясений или ускорить момент наступления каких-либо положительных событий.

Для оценки экономического и социального благосостояния какой-либо территории на протяжении многих лет выделяют такой показатель, как ВВП (аналогом для субъектов хозяйствования более низкого уровня является величина ВРП) [1; 2]. Он предназначен характеризовать динамику экономического роста. При оценке субъектов хозяйствования по данной метрике определяются наиболее развитые территории.

В соответствии с этим важной научной проблемой является поиск «рычагов» регулирования, то есть перед научным сообществом стоит задача выделить факторы, изменяя которые можно увеличить или снизить величину ВВП (ВРП), а следовательно, повлиять на экономический рост или развитие.

К ключевым факторам подобного рода относят научно-технологический (в более старых источниках «научно-технический») прогресс и сопряженную с ним инновационную деятельность предприятий и организаций [3; 4; 5]. По мнению ряда авторов [6–11], наука и технологии являются двигателем социально-экономического развития, следовательно, государству, для того чтобы повысить свою конкурентоспособность на международной арене, а также улучшить условия проживания граждан на конкретно взятой территории, стоит реализовывать политику, направленную на поддержку науки и исследовательского сектора [12; 13; 14].

В соответствии с этим разрабатываются различные экономико-математические модели [15; 16] (Р.М. Солоу [8], С. Ребело [9], К. Эрроу [17], П.М. Ромер [18], Р. Лукас [19], Д. Гроссман и Э. Хелпман [20], К. Фримен и Б.-А. Лундвалл [21], Ц. Грилихес [22]), которые в зависимости от выбранных и обоснованных учеными и исследователями показателей описывают функциональные связи между экономическим ростом и каким-либо экономическим объектом (затраты на науку; количество проводимых научно-исследовательских и опытно-конструкторских работ; человеческий капитал; предприятия, осуществляющие и реализующие инновационную деятельность; образовательные учреждения; динамика инновационных идей). Данные модели имеют как теоретическое обоснование на уровне гипотез, так и некоторую эмпирическую реализацию, что в определенной мере является их апробацией и подтверждением сформулированных идей.

Учеными в этом направлении также предпринимаются попытки комплексной оценки научно-технологических изменений в экономической среде. Для этого разрабатываются и рассчитываются различного рода «интегральные» оценки. Примером может служить индекс научно-технического потенциала региона, методика расчета которого опубликована в работах К.А. Задумкина и И.А. Кондакова [23], или оценка научно-технологического потенциала территорий, представленная в статье коллектива авторов под руководством К.А. Гулина [24]. Довольно серьезным и фундаментальным трудом является проект Рейтинга инновационного развития субъектов Российской Федерации, разработанный и публикуемый с 2012 по 2019 год коллективом авторов Института статистических исследований и экономики знаний, входящего в состав ВШЭ ¹ . Данная методика включает оценку 37 показателей, а также имеет значительный временной период расчета (7 лет).

В целом стоит отметить, что в вышеперечисленных работах в различной мере предпринимались попытки оценить совокупное влияние факторов научно-технологического и инновационного развития на социально-эко- номический уровень территорий (России как отдельно взятого государства и округов или регионов, входящих в ее состав, представляющих аналогичные единицы меньшего размера). В результате комплексности полученных оценок их интерпретация представляет собой некую условную единицу, характеризующую некий обобщенный процесс или явление (в нашем случае научно-технологический потенциал, инновационное развитие и др.), но не имеющую явной количественной интерпретации, которая может быть получена в ходе проведения измерительных процедур. В результате возникает вопрос об адекватности и достоверности описываемых процессов такими интегральными оценками. Их достоверность может быть подтверждена только по истечении какого-либо времени, что существенно снижает значимость и прикладную применимость подобного рода моделей.

С потребностью оценивания объектов, которые характеризуются неоднородными параметрами, человек сталкивается достаточно часто. Чаще всего подобная оценка проводится интуитивно, как следствие, имеет место отрицательный итог. Использование самих интегральных оценок также сопряжено с рядом проблем, которые могут быть охарактеризованы следующим ² [25; 26; 27]:

– необходимость учета веса и значимости каждого из параметров, включенного в состав общей оценки;

– необходимость задать способ перевода качественных оценок в количественный вид;

– распределение оцениваемых объектов в соответствующие группы, характеризуемые величиной выделенных в исследовании уровней;

– возможность сравнения оценок с теми, которые будут получены в будущем (социальноэкономические показатели зачастую имеют непостоянную природу и с течением времени могут быть не актуальны в отличие от физических величин, которыми измеряются объекты естественных наук).

Описанные выше проблемные аспекты интегральных оценок также обозначены в ряде отечественных научных работ, где предпринята попытка систематизации достоинств и недостатков подобного подхода относительно интерпретации объектов социальноэкономического характера. Так, в статье Е.Н. Волковой на основе интегральной оценки сформирована и описана методология характеризации социально-экономического развития региона [28]. В работе Е.В. Клюшниковой и Е.М. Шитова обозначены особенности построения интегральных оценок в соответствии с основными этапами моделирования: нормирование, агрегирование, взвешивание [29]. За рубежом проводятся аналогичные исследования. Одной из подобных работ является публикация коллектива ученых под руководством М.-С. Саиба [30], в которой авторы посредством интегрального показателя оценивают неравенство населения территорий относительно условий и факторов воздействия на здоровье.

Из современных работ особое внимание следует обратить на публикацию А.А. Сидорова [31]. Он скрупулезно систематизирует и описывает математическую природу интегрального подхода, в некоторой мере продолжая работы известного российского эконометриста С.А. Айвазяна [32; 33; 34]. В зарубежной среде также присутствуют исследования, связанные с математическим построением интегрального показателя. Так, в статье коллектива авторов под руководством П. Чжоу [35] предложен вариант агрегирования интегральной оценки на основе произведения скорректированных частных значений показателей, входящих в нее.

Несмотря на большое многообразие работ по использованию интегрального подхода применительно к социально-экономическим объектам, в них опускается один момент – правильно ли интегральные показатели характеризуют то, что предназначены описывать? Хотя практически во всех просмотренных исследованиях оговаривается, что подобного рода оценки несут в себе изрядную долю неопределенного субъективизма.

В связи с этим в статье поставлена цель определить достоверность искусственно выведенных интегральных комплексных оценок посредством математико-статистических методов, которые, в свою очередь, описывают различные процессы и явления социально-экономического характера.

Под «достоверностью» обозначенных в работе оценок мы будем понимать их способность в явном виде описывать те процессы и явления, которые они должны характеризовать.

Для достижения поставленной цели в работе решен ряд задач:

– определены и описаны методы математической статистики, с помощью которых осуществлен поиск взаимосвязи между экономическим ростом и оценкой научно-технического развития;

– сформирована выборка данных для обозначенных в работе расчетов;

– проведены и описаны результаты расчетов, на основании которых были сформулированы соответствующие выводы и рекомендации.

Методы исследования

Алгоритм однофакторного дисперсионного анализа

В математической статистике дисперсионный анализ используется для исследования наличия влияния качественных факторов на значения количественного показателя. В нашем случае за результирующий показатель выступит y :ВРП, а за фактор х: хЕ (/ 1 ||/ 2 ),(/ 1 ||/ 2 ) з 5 1 &5 2 &5 з &5₄ , где 1 1 -российский региональный инновационный индекс, I ₂ – комплексная оценка научнотехнологического потенциала, а (S _n } „₌₁ — входящие в их состав субиндексы.

При помощи однофакторного дисперсионного анализа попробуем определить, является ли статистически значимым различие y в субъектах Российской Федерации, отличающихся по признаку I , наблюдаемом на k = 4 уровнях (социально-экономические условия, научно-технический потенциал, инновационная деятельность, качество инновационной политики в одном случае и исследования и разработки, кадры, технологии и инновации в другом).

Алгоритм формирования выборок для проведения однофакторного дисперсионного анализа

Алгоритм отбора элементов четырех различных выборок в соответствии с уровнями I1 сформируем на основе рейтингов субъектов Российской Федерации по субиндексам российского регионального инновационного индекса. Полученные учеными и исследователями ИСИЭЗ распределения включают в себя четыре группы, которые можно охарактеризовать следующим образом (группы смоделированы авторами рассматриваемого исследования, но в них отсутствует явное обоснование пограничных значений; вариант возможной интерпретации представлен далее):

I группа – города федерального значения (Москва, Санкт-Петербург), имеющие наилучшие показатели по большинству статистических метрик, характеризующих социальноэкономическое развитие. По своей природе их оценки разнятся с другими аналогичными объектами (региональные территориальные единицы) в несколько раз, из-за чего они явно выбиваются из общей картины распределения и выглядят как выбросы. В связи с этим при проведении однофакторного дисперсионного анализа они будут исключены из нашего исследования, что позволит оценить действительно равнозначные объекты между собой;

II группа – региональные территориальные субъекты, обладающие наилучшими значениями по оцениваемым признакам (за исключением объектов, входящих в I группу), зачастую превышающими средние общероссийские оценки. Подобные субъекты могут расцениваться как те, которые в полной мере обладают наличием рассматриваемого признака;

III группа – регионы РФ, зачастую имеющие значения по S _n оценкам, меньшие, чем среднероссийские характеристики; данные территории только подбираются к качественному уровню исследуемых признаков I и поэтому не могут считаться в полной мере обладающими исследуемыми характеристиками, а значит, их следует исключить из дальнейших расчетов;

IV группа – территориальные единицы с наименьшими значениями по рассматриваемым признакам; их можно охарактеризовать сильным разбросом оценок в разрезе динамики, нестабильностью темпов роста и отсутствием явно выраженных трендов; в связи с этим в исследуемую выборку подобные объекты включены не будут.

Алгоритм отбора элементов четырех различных выборок в соответствии с уровнями I2 сформируем на основе рейтингов субъектов Российской Федерации по субиндексам оценки научно-технологического потенциала территорий. Полученные учеными и исследователями ВолНЦ РАН распределения включают в себя пять групп (уровни: высокий, выше среднего, средний, ниже среднего, низкий), которые можно охарактеризовать как равнораспреде-ленные отмасштабированные до целого десятка (/2 е [0;10]).

В соответствии с названным выше правилом включения наблюдений в дисперсионный анализ (по аналогии с рейтингом субъектов Российской Федерации) нас интересуют группы «среднего» и «выше среднего» уровня. В них, как и в предыдущем варианте, мы подразумеваем присутствие рассматриваемой интегральной комплексной оценки, следовательно, данные наблюдения должны найти отражение в изменении динамики ВРП. Территории, вошедшие в выборку с высоким уровнем, являются уникальными единичными объектами и своего рода представляют выбросы. Группы «ниже среднего» и «низкого» уровня включают в себя основную часть наблюдений и, по сути, представляют собой идентичные объекты без каких-либо характерных особенностей (на 2015 год их доли в выборке в соответствии с выделенными группами субиндексов составили 93,75; 95; 95 и 98,75% соответственно).

На этом алгоритм формирования выборок заканчивается, и дальше продолжается алгоритм однофакторного дисперсионного анализа.

Осуществив выборку регионов РФ, определим количество объектов, включенных в каждый из k уровней ( k = 4 ) как сумму элементов, входящих в рассматриваемую совокупность, и обозначим ее через m_n , где n – порядковый номер уровня.

Затем определим общее количество ( m ) вошедших во все выборки объектов (формула 1):

т

- I

к т_п

Далее рассчитаем среднее значение ВРП по каждой из сформированных групп k (формула 2):

У п =

1 ^~1^тп т_п^1 =1^Ут

где y_ni – значение ВРП, соответствующее i региону в выборке n .

На следующем шаге найдем среднее значение результирующей переменной y по всем имеющимся значениям, входящим во все выборки n (формула 3):

1 ^”1^ ^”1тП 1 ^”1^

'=sZ ,., ! ,.,^- "”! ,.,⁵⁵⁵ ™ " . (3)

Дальнейший этап – поиск суммы квадратов отклонений результирующих оценок ( y_ni ) по выборкам от общего среднего ( у ) (формула 4):

Z k y¹™”

..Z .'-■                   ⁽⁴⁾

Затем – сумма квадратов отклонений средних по группам ( у^ ) от общего среднего значения ( у ) (формула 5):

Z k

(У п - y)²m _n .

П=1

Далее рассчитаем остаточную сумму квадратов отклонений как сумму квадратов разности результирующих значений ( y_ni ) от средних значений ( у ), входящих в одну и ту же выборку n (формула 6):

Z k -^-imn

/   (Уп; - Ю2.(6)

п=1^-й=1

Для проверки S ² (формула 4) может быть использовано следующее равенство (формула 7):

S) + S2ct = S2.(7)

Вычислим факторную дисперсию (формула 8):

^ 2

° = гл.

Вычислим остаточную дисперсию (формула 9):

иост

ост т — к .

Далее найдем значение F _ф по формуле частного факторной дисперсии (а р ) к остаточной (ар ст ) (формула 10):

Ор

^ Ф =     .                   (10)

Оост

Используя распределение Фишера – Снеде-кора, при заданном уровне значимости (α) и двух степеней свободы (формулы 11 и 12) можно определить значение метрики Fк:

#1 = к- 1 ;             (11)

df2 = т-к .             (12)

Для поиска F _к могут применяться классические таблицы распределения Фишера – Снеде-кора, фигурирующие в справочниках по математической статистике, но при их использовании ученый может столкнуться с рядом проблем. Это отсутствие необходимых числовых значений, на которых строится исследование, и схожая ситуация, связанная с выбором уровня надежности (зачастую в справочной литературе присутствуют лишь а: а = 0.1||0.05||0.01 ) . Подобную проблему в настоящий момент несложно решить, используя возможности вычислительных компьютерных программ (например, функция « F_k » библиотеки Python «Scipy»).

По итогу необходимо сравнить полученные значения Р ф &Р_К (формула 13):

^ ф >  F_K ^ А ,             (13)

где А – утверждение о том, что исследуемые качественные признаки действительно оказывают влияние на величину результирующего показателя.

Алгоритм корреляционного анализа

детерминации ( R ² ), который может быть найден по следующей формуле (формула 17):

2-S-^ R = SS ,

rxy

COVxy ^у

где cov_xy = M ((х п - ^Х п ))(у п - ц(у_п ))} ~ ⁽ 1 ⁴⁾

~ M(x _n y _n ) - ц(у п MxJ;

M() — несмещенная оценка математического ожидания по выборке;

^() — среднее значение исследуемых наблюдений.

Алгоритм построения модели множественной линейной регрессии

Модель множественной линейной регрессии является инструментом, используемым в многомерном статистическом анализе для описания связи признаков (причин) с каким-либо результатом или следствием. Ее общий вид представлен аналитической формулой (формула 15):

^у = ⁰О + ⁰1^х1 + 0 2 % 2 +-----И 0_лх_л +— ,   (15)

где ^{ 0 п ) п=1 — коэффициенты регрессии, показывающие степень воздействия фактора на результирующий признак;

0 0 — свободный параметр модели, позволяющий оптимальным образом расположить кривую в пространстве таким образом, чтобы сумма квадратов отклонений (МНК) была наименьшей.

Для расчета коэффициентов β удобно использовать матричный метод поиска (формула 16):

®=6

^ 11

^ 21

Xz1

^ 12

Х22

Xz2

% 1 _П\ ^ 271

% zn/

/ ИЛ А Ш VJ

^

^ В = (X^TX)^-1X^TY .

После построения самой модели необходимо оценить ее точность и значимость. Точность модели множественной линейной регрессии определяется при помощи коэффициента

где Юф = ^ _ ^(y_t - у)²

–

объясненная

сумма квадратов регрессии;

SS = ^  (У£ - У)2 — общая сумма ква дратов регрессии;

j – порядковый номер наблюдения, входящий в формируемую модель.

Чем ближе данная метрика к единице, тем лучше построенная модель аппроксимирует имеющиеся эмпирические данные.

Для сравнения точности идентичных моделей, различающихся по количеству регрессоров, используют другую метрику, так как коэффициент детерминации, рассчитанный способом по формуле 17, будет всегда лучше при большем количестве параметров. Для сравнения качества подобных регрессий следует использовать скорректированный R ² (формула 18):

R2aaj = 1

—

(1 — R^) • (z — 1) z — n — 1

.

На финальном этапе оценивается значимость построенной модели. Она определяется при помощи F -критерия Фишера. Для этого необходим требуемый уровень значимости ( α ) и рассчитываем следующие характеристики (формула 19):

SSo = yz (yt-yt )2^ss-ss^ 4—1 j=1

остаточная сумма квадратов регрессии;

(df 1p = n)

/        SS*            SS0 \   z ч

(MS ф =      & MS₀ = -7^) ^ (F^ p

\ ^ф #1 p          df2pj      ^p

–

– чис-

М5 ф MS₀ .

Определение ( F _K ) _p происходит аналогично процедуре по поиску ( F _K ), только в этом случае вместо dfl (формула 11) и ^2 (формула 12) берутся соответственно df1_p&df2_p (формула 19). Затем аналогично формуле 13 сравниваются новые полученные соответствующие значения.

Алгоритм определения значимости коэффициентов множественной линейной регрессии

Для того чтобы определить значимость коэффициентов множественной линейной регрессии, используют t -критерий Стьюдента. Он позволяет дать ответ на вопрос: «Могут ли коэффициенты, полученные в модели, быть интерпретированы?»

Наблюдаемые значения, полученные из построенной статистической модели, рассчитываются при помощи стандартной ошибки параметров (/ ^ 0 &  Ц^ ) р₀ & р_л соответственно (формула 20):

.       Р0 о         Рп ..

ч=v t=tp°||t/?n.(20)

Стандартные ошибки могут быть найдены из формулы 16 через матрицу А (формула 21):

Л = (ХтХуг .(21)

Данная матрица является квадратной и определяется размером (к + 1) х (к + 1) . Следовательно, ее диагональный элемент может быть обозначен как а _пп . Тогда (формула 22):

lPo2 = MSoa00, lpn2 = MSoann, п = 1, к, к = 4.

Полученные в формуле 21 значения сравниваются с двусторонней критической точкой распределения Стьюдента — t_K(a; z — п — 1). При |t| > t_K соответствующий параметр множественной линейной регрессии считается статистически значимым, нулевая гипотеза вида H 0 : /?₀||/?_п = 0 отвергается.

Алгоритм построения логистической регрессии

При помощи данного метода может быть определена потенциальная вероятность наступления какого-либо события, в нашем случае – вероятность роста динамики ВРП в зависимости от совокупного годового изменения k -факторов.

В общем виде модель выглядит следующим образом (формула 23):

Р = р₀ + р 1 • ДХ 1 +

+ Р 2 • Д% 2 + - + р_п • ДХ_П + - ,

где Р — предварительная оценка вероятности наступления определенного события;

{Р п } и=0 — коэффициенты регрессии, аналогичные тем, которые характеризуют модель (формула 15);

{Дх_п} ^= ₁ — значения годового изменения соответствующего фактора.

Итоговое преобразование (Р'^-) может быть осуществлено через функцию sigmoid, и выглядит так (формула 24):

Р' = sigmoid^P^ = ^—-— -^ .

Алгоритм преобразования годовой динамики ВРП в значения булевой функции

Если y – значение ВРП в настоящий момент, а y ^–1 – в предыдущий, то ∆ y – благоприятная динамика y по абсолютному отклонению от y ^–1 . Тогда может быть получено P (формула 25):

.     „    1, если Ду > 0          , ч

Ду ^ -Р - [о, если Ду < о .         ⁽²⁵⁾

В соответствии с обозначенными выше методами далее представлены необходимые статистические формы, которые были разработаны авторами для проведения соответствующих статистических оценок, а также расчетные результаты и вытекающие из этого комментарии, выводы и заключения.

Результаты

Дисперсионный анализ

Для проведения дисперсионного анализа по алгоритму, описанному в первом пункте «Методов исследования», был сформирован массив данных (табл. 1) , где представлены значения ключевых субиндексов (социальноэкономические условия, научно-технический потенциал, инновационная деятельность, качество инновационной политики), входящих в общую оценку «Рейтинга инновационного развития регионов», разработанного ИСИЭЗ, и аналогичных показателей (исследования и разработки, кадры, технологии, инновации) по оценке научно-технологического потенциала ВолНЦ РАН. Данные взяты в соответствии с последними актуальными расчётами, проводимыми на момент описанного в работе исследования за 2015 год.

Таблица 1. Часть апостериорного набора данных для проведения однофакторного дисперсионного анализа

CD a OQ О x О El 3 >3 X о 3 ro 03 о X 3 >3 X ro X о 3 о О. >3 3 X о >3 3 о о о О-

>3 о 1 = g i    я 1 S         II S §     £- О с 03 I— О CD X ГО ^

co

co

co

CD

co CM II e’

X Q-=r X о OQ ro ro X о I— о о о CD 3 X X о 1— 6 X го X го X X о о

3 3 го      'чГ 3    и X   ^. X

II s’

> 1 1 ё 3 ^ см ^ О) со тт >    CD В О- см \ -J Г-« § о "го см го о ° — СО CD О СО СМ О) а 2 N СМ ^ Щ со & 1 го х =1 Н Го CD      ZE > g “ S Z x co _ о LO    О ro CD о   X E   - CD C X ^ CD. IS I ssb 5. 2    m CD o го o o g CM m       CD -ac      m ^" ze о i— ro x ro S § о о g ° Го lZ ш Q, cd H g x       ГО ° ro о. о Я 03 S CD DZ 3 ° H ± x g    z CD U? m s S “ no О н ^ 511 it illl l ¥ ■ ■ S й 5 ° S      i § о ¥ 5 8 $ 5 g ” о ГО о cd "°| ° ° | ^ e

g z     co s 4

§

co

LO II E"

3 3 О     со' о       II х      с: X    '—" о н

со II е"

>3 3 X о X           CM s «   ^ X ro X

co

s

co E~

о.  ™ сс       II S    -Е-

со II Е~

о 3 >3 5 S ° g   — S Э z    t— ? 1 5    ё HI ~ = ro о >. О

CD

co

co CM II E"

I 1 $ о O'S II 5 g-^ X

II Е""

>3 5 'S. i z CD uZ     ^ Q. 5 ,= & ro □Q

CD

s

co

n

§

co

co

co

CM co II E

II Е

DZ d го о ii 2 о 3 CD 1-

I

ro 5

ro ro CD

Й ro П CD

ro CD

ro S

ro S"

Й ro ro

ro

ro

О X О CD <0 О О s о 5C X Q-3 О d VO о з

о X о CD <0 О О з о X X Q-3 О d \О о 3 ^ го

Таблица 2. Результаты, полученные в ходе проведения дисперсионного анализа

Наименование показателя	Единица измерения	Символьное обозначение	Расчетное значение
			I 1	I 2
Среднее значение ВРП по группе S 1	млн руб.	У1	1 183 444	1 204 667
Среднее значение ВРП по группе S 2	млн руб.	У 2	1 338 762	1 577 121
Среднее значение ВРП по группе S 3	млн руб.	Уз	1 810 813	4 743 038
Среднее значение ВРП по группе S 4	млн руб.	У4	1 181 169	837 495
Среднее значение ВРП по всем объектам, отобранным в выборки	млн руб.	У	1 327 875	2 237 876
Значение расчетной статистики Фишера	усл. ед.	F ф	0.4422	0.4837
Значение критической статистики Фишера	усл. ед.	F К	2.7218*	4.3468*
* При α = 0.05. Составлено по таблице 1.

В каждую из четырех групп вошли те значения ВРП регионов, для которых соблюдалось условие попадания соответствующего индекса по группе значимости – II группа для методики ВШЭ и группы уровня «средний» и «выше среднего» для методики ВолНЦ РАН.

В соответствии с формулами 1–13 и апостериорным набором данных из таблицы 1 получены статистические метрики (табл. 2) , которые могут быть использованы для интерпретации проведенного в работе дисперсионного анализа на предмет определения значимого влияния субиндексов рассматриваемых методик на уровень экономического роста территорий, выраженного в значениях показателя ВРП.

В ходе проведения дисперсионного анализа проверялась гипотеза о наличии воздействия и влияния искусственно выведенных интегральных оценок рейтинга российского регионального инновационного индекса и оценки научно-технологического потенциала на величину валового регионального продукта территорий (динамику экономического роста). При отборе территорий, где были зафиксированы соответствующие оценки по каждому из четырех субиндексов для каждой из методик, были соответственно сформированы восемь выборок, характеризующихся высоким проявлением процессов, присущих одной из четырех ключевых групп исследуемых рейтингов.

Расчетное значение F -статистики как в одном, так и в другом случае ( F _ф1 = 0.4422, F _ф2 = 0.4837) оказалось в значительной мере меньше критического значения ( F _K1 = 2.7118, F _K2 = 4.3468) при заданном уровне надежности в 5% и полученных соответствующих степенях свободы (#1_1||2 = 3 & (#2 ! = 78 || df2 2 = 7))

(см. табл. 2). Из этого может следовать вывод, что различия между группами регионов, вошедших в выборки по большим значениям (но не максимально возможным) ключевых индикаторов рассматриваемых методик являются статистически незначимыми в отношении различий по величине ВРП. В первую очередь это может указывать на два момента: либо данные индикаторы не оказывают существенного влияния на изменение экономического роста регионов, либо сравниваемые комплексные оценки являются взаимообусловленными.

Панель данных для проведения корреляционного анализа, построения множественной линейной регрессии и логит-модели

Для проведения выделенных анализов и вариантов моделирования была сформирована статистическая панель, сопоставляющая значения изменений динамики субиндексов Рейтинга инновационного развития субъектов Российской Федерации и оценки научнотехнологического потенциала территорий РФ ( ∆ n – столбец 8 и др. табл. 3 ) с фактом положительного роста динамики ВРП (столбец 5 табл. 3). Сформированные данные использованы при проведении корреляционного анализа, где была задействована информация по субиндексам в 2015 году (столбец 7 и др. табл. 3) и соответствующим данным, характеризующим значения ВРП в этот год (столбец 4 табл. 3). Этот же набор данных использован и при построении модели множественной линейной регрессии. Для создания логит-модели необходимо было установить факт роста ВРП (столбец 5 табл. 3), как положительного отклонения к предыдущему году при абсолютном отклонении факторов (столбец 8 и др. табл. 3), потенциально оказывающих влияние на этот процесс.

Таблица 3. Часть апостериорного набора данных для проведения корреляционного анализа, построения модели множественной линейной и логистической регрессии

ос    7 CD   J s s   сс га      о ^ го  S S' S   ® I   О Ко.  го => 1=   О 5    — 1 5    ZE   У CD S    >^ S 7  5 га < s-^ е § S о Н га    у О 8  S о S'   ,s □i о га CD                 CD    . га" 03 пс 5 m cd     ° cxj го I °  g^ l^o  co 5-0  Яго о га       _ В- cz о     ос SpS 5 2 ii ^ ll га   о   g ^  о  га -j-1  га  га *  о IE га О x

и 1 <85

со

ср

го

2

Q

ГО

Го

2

5 S CD П S ^ cz 7 §

со

CD

ср

CD

го

Го

Го

Го

а>

го

га 5 CD II S ^ cz 7 g

со

ср

го

CD

го

го

CD

Го

Го

CD

Го

5

го

^

^

\

\

^

^

\

Z

^

^

со

га-

го

CD

2

Го

от

га EZ СО

ср

со

го

со

S

го

ГО

2

2

см

со

CD

ГО

го

Го

СО

со

Го

I

га

га

га 5

га g га CD in

га ш

га га со

га га с; CD

га со

га S

Корреляционный анализ

Матрица из таблицы 4 характеризует линейную взаимосвязь между результирующим показателем экономического роста региона (ВРП) и индикаторами, являющимися ключевыми субиндексами Рейтинга инновационного развития субъектов Российской Федерации. Анализ данных проведен на основании статистики за 2015 год.

В соответствии с каждым из ключевых показателей Рейтинга инновационного развития субъектов РФ и величины ВРП, присущей рассматриваемым территориям, сделан ряд соответствующих выводов.

• 1)    Валовой региональный продукт

Прослеживается линейная связь между социально-экономическими условиями деятельности. Обнаружен отклик от значений показателя, характеризующего научно-технический потенциал. Показатели, описывающие уровень инновационной деятельности и качество инновационной политики, линейно практически никак не отражаются на росте или снижении экономического роста регионов РФ.

• 2)    Социально-экономические условия инновационной деятельности

Данный показатель сильно коррелирует со значениями показателя, характеризующего научно-технический потенциал регионов РФ. Этим может быть обусловлена высокая корре- ляционная связь между ВРП и научно-техническим потенциалом. Прослеживается связь с показателями инновационной деятельности, с качеством инновационной политики – несущественная.

• 3)    Научно-технический потенциал

Значения данного показателя коррелируют со значениями показателей, характеризующих инновационную деятельность регионов России. Прослеживается более сильная связь с качеством инновационной политики, чем у предыдущих показателей.

• 4)    Инновационная деятельность и качество инновационной политики

Данные показатели в большей мере коррелируют между собой, нежели остальные.

Общий вывод

Из всего этого следует, что есть явно выраженная взаимообусловленность между рассматриваемыми метриками. Это подтверждает выводы, полученные в ходе проведения дисперсионного анализа, который показал отсутствие статистически значимой разницы между величиной ВРП объектов, входящих в разные категориальные группы по уровням инновационного развития регионов.

Матрица из таблицы 5 характеризует линейную взаимосвязь между ВРП и ключевыми субиндексами рейтинга, оценивающего научно-технологический потенциал территорий (2015 г.).

Таблица 4. Результаты проведенного корреляционного анализа по методике ИСИЭЗ

	ВРП	n 1	n 2	n 3	n 4
ВРП	1	0.6669	0.4540	0.2652	0.1571
n 1	0.6669	1	0.5905	0.3935	0.2289
n 2	0.4540	0.5905	1	0.4007	0.2897
n 3	0.2652	0.3935	0.4007	1	0.4892
n 4	0.1571	0.2289	0.2897	0.4892	1
Составлено по таблице 3.

Таблица 5. Результаты корреляционного анализа, проведенного по методике ВолНЦ РАН

	ВРП	n 1	n 2	n 3	n 4
ВРП	1	0.6674	0.6862	0.4558	0.3051
n 1	0.6674	1	0.8034	0.8205	0.3481
n 2	0.6862	0.8034	1	0.6430	0.2631
n 3	0.4558	0.8205	0.6430	1	0.3783
n 4	0.3051	0.3481	0.2631	0.3783	1
Составлено по таблице 3.

• 1)    Валовой региональный продукт

В соответствии с практикой эконометрического моделирования связи ВРП с показателями, которые выбраны в качестве предикторов, слабые и не могут быть в должной мере использованы для прогнозирования или интерпретации движения динамики результирующей оценки как линейного отклика от них.

• 2)    Исследования и разработки

Группа показателей, имеющая наибольшие коррелирующие значения по всем исследуемым наборам субиндексов методики ВолНЦ РАН. Значительный ее уровень наблюдается для показателей групп «Технологии» (0.8) и «Инновации» (0.82). При этом сами эти группы между собой коррелируют значительно меньше (0.64), что, возможно, может быть успешно использовано для построения модели множественной линейной регрессии, где в качестве результирующей оценки выступят «Исследования и разработки». Однако это также указывает, что данные третьей группы в значительной мере дублируют друг друга.

• 3)    Технологии

Слабая линейная связь с группой показателей «Инновации» и «Кадры».

• 4)    Инновации

Практически отсутствующая линейная связь с последней группой показателей, характеризующих абстрактную систематизацию научных кадров.

Общий вывод

Наблюдается ситуация, аналогичная случаю с корреляционным анализом, проведенным по рейтингу оценки инновационного развития субъектов РФ. Как особый момент следует выделить связь показателей групп «Технологии» и «Инновации» с «Исследованиями и разработками». Тем не менее все так же присутствует сильная взаимообусловленность одних метрик с другими, используемыми для расчета конечной результирующей оценки, что указывает на необходимость применения эффективной методики поиска весов при формировании итогового расчета, либо снижения размерности количества предикторов за счет исключения несущественных факторов.

Множественная линейная регрессия

Таблица 6 отражает основные статистические метрики полученных результатов по по- строенным в работе статистическим моделям множественной линейной регрессии, а именно параметры регрессионной модели, как базовые, так и модифицированные; коэффициенты детерминации и их скорректированную оценку; расчетную и критическую F-статистику Фишера при заданном уровне надежности 5% и оценку значимости полученных параметров моделей с использованием t-статистики.

График фактических значений величины ВРП регионов в 2015 году, отсортированных по возрастанию значений субиндекса Рейтинга инновационного развития субъектов России (рис. 1) , характеризующего социально-экономические условия для реализации и ведения инновационной деятельности в территориальных субъектах страны, представлен далее. Данное ранжирование обусловлено наличием в модели аппроксимирующей значения ВРП по единственному параметру, указанному выше. В связи с этим можно попробовать графически отобразить зависимость исследуемой величины (валовой региональный продукт) от конкретно установленного предиктора (интегральная оценка социально-экономических условий инновационной деятельности).

Так как значение F расчетной статистики ((^ ф ) = 16.3967) больше критического значения ((F _K ) _p = 2.4859) при заданном уровне значимости в 5%, то гипотеза об одновременном равенстве нулю всех предикторов в регрессионной модели отвергается, т. е. построенная базовая статистическая модель является статистически значимой (см. табл. 6). Но при более детальном ее рассмотрении и проведении тестов для полученных параметров на t -статистику были идентифицированы смещенные оценки. Из пяти коэффициентов, включая «intercept», значимыми оказались лишь два: «intercept» и параметр β ₁ , характеризующий социально-экономические условия инновационной деятельности. Из модифицированной модели были исключены незначимые параметры ( β ₂ – научно-технический потенциал; β ₃ – инновационная деятельность; β ₄ – качество инновационной политики), и получена новая статистическая модель, соответствующая условиям F и t статистики. Также удалось увеличить значение скорректированного R ² с 0.42 до 0.44.

Таблица 6. Результаты регрессионного моделирования

Наименование показателя	Символьное обозначение	Расчетное значение
		/ 1	/ 2
1. Базовая регрессионная модель: у = р 0 + р 1 х 1 + р 2 х 2 + р 3 х 3 + р^
y I1 = -3964780.87 + 11310999.28x 1 + 1854358.59x 2 - 173667.55x 3 - 50769.69x 4
y l2 = -663095.39 + 564364.88x 1 + 533221.86x 2 - 335361.73x 3 + 201959.81x 4
intercept	Д о	-3 964 780.9	-663 095.39
Расчетная t -статистика для Д о	^0	6.2250	2.7310
Социально-экономические условия инновационной деятельности / Исследования и разработки	Д	11 310 999	564 364.88
Расчетная t -статистика для Д 1	^1	5.8615	3.0278
Научно-технический потенциал / Кадры	Д а	1 854 358.6	533 221.86
Расчетная t -статистика для Д 2	^2	0.9157	3.1671
Инновационная деятельность / Технологии	Д з	-173 667.55	-335 361.73
Расчетная t -статистика для Д 3	^3	0.1326	2.1266
Качество инновационной политики / Инновации	д	-50 769.69	201 959.81
Расчетная t -статистика для Д 4	^4	0.0564	1.4406
Критическая точка распределения Стьюдента	t k	1.9901	1.9921
Коэффициент детерминации	R2	0.4505	0.5437
Скорректированный коэффициент детерминации	Radj	0.4230	0.5194
F -критерий Фишера расчетный	(Ч	16.3967	22.3439
Критическое значение распределения Фишера	Фк ) р	2.4859	2.4936
2. Модифицированная регрессионная модель: у^ = р 0' + р 1 х 1
y I 1 = -3813320.76 + 12243723.31x 1
Новый intercept	Д о'	-3 813 320.76
Расчетная t -статистика для Д о'	t «o'	6.5117
Социально-экономические условия инновационной деятельности (несмещенная оценка)	Д 1'	12 243 723.31
Расчетная t -статистика для Д'	t «i'	8.1531
Новая критическая точка распределения Стьюдента	t k	1.9890
Новый коэффициент детерминации	R2'	0.4447
Новый скорректированный коэффициент детерминации	R adj'	0.4380
Новый F -критерий Фишера расчетный	(Ч'	66.4736
Новое критическое значение распределения Фишера	Фк ) р'	3.9560
3. Модифицированная регрессионная модель: у^ = р 0' + р 1 х 1 + р 2' х 2
y I 2 = -393469.1 + 346573.61x 1 + 543161.88x 2
Новый intercept	Д о'	-393 469.10
Расчетная t -статистика для Д о'	t P o '	2.0592
Исследования и разработки (несмещенная оценка)	Д 1'	346 573.61
Расчетная t -статистика для Д'	t 3 1 '	2.4416
Кадры (несмещенная оценка)	Д 2'	543 161.88
Расчетная t -статистика для Д'	^ 82'	3.1554
Новая критическая точка распределения Стьюдента	t k'	1.9912
Новый коэффициент детерминации	R2’	0.5090
Новый скорректированный коэффициент детерминации	Radj'	0.4962
Новый F -критерий Фишера расчетный	(4'	39.9059
Новое критическое значение распределения Фишера	Фк ) р'	3.1154
Составлено по таблице 3.

Рис. 1. Графическая визуализация регрессионного моделирования по методике ВШЭ

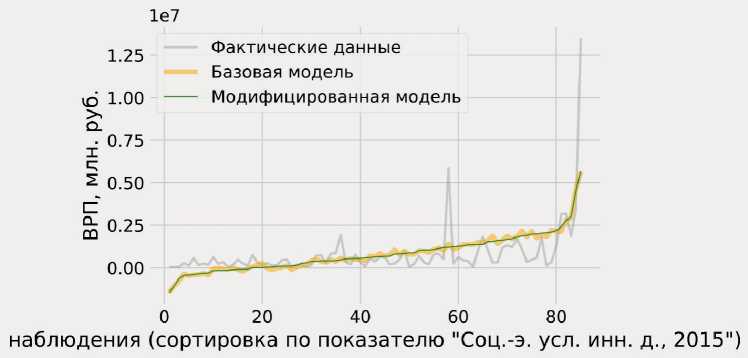
Составлено по таблице 3.

Рис. 2. Графическая визуализация регрессионного моделирования по методике ВолНЦ РАН

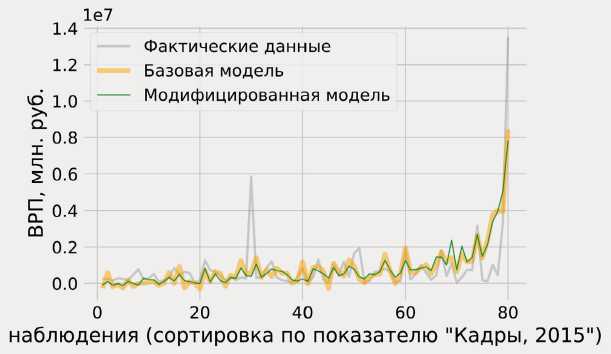
Составлено по таблице 3.

Аналогично предыдущему представлены результаты моделирования по методике ВолНЦ РАН (рис. 2) . Сортировка результирующих и фактических значений ВРП проведена по показателю «Кадры» в соответствии с наибольшим значением, полученным при расчете его t -статистики (3.1554).

При первичном осмотре можно отметить, что регрессии, построенные по второму исследуемому показателю ( I ₂ ), более точно повторяют динамику фактических значений ВРП. Об этом свидетельствует и скорректированный коэффициент детерминации ^Radj'(^ = 0.4962 больший ^/(/J = 0.4380 .

Данный момент, возможно, обусловлен снижением размерности включенных во вторую методику показателей, из-за чего не так сильно выражено усреднение исследуемых оценок. В какой-то мере это является преимуществом методики ВолНЦ РАН по отношению к той, которую разработали исследователи ВШЭ.

По модифицированной регрессии у / 2 в сравнении с y j 1 можно также отметить, что она имеет большее количество степеней свободы (на один предиктор). Это дает ей соответствующую гибкость и независимость при прогнозировании результирующей оценки.

Таблица 7. Результаты регрессионного моделирования логит-модели

Наименование показателя	Символьное обозначение	Расчетное значение
		/ 1	/ 2
Логистическая регрессионная модель: Р' =----,                     _ _ " "                ri            1 + е-(ро+р1^ДХ1+Р2^ДХ2+Рз^ДХз+Р4^ДХ4)
1
к 1 + е-(0.7466-1.4252'Дх1+1.8070'Дх2-1.7907-Дх3 + 0.3162-Дх4)
Р',
к 1 + е-(0.7111+0.0775'Дх1 + 0.1452-Дх2-0.1321-Дх3+0.1373-Дх4)
intercept	Р о	0.7466	-0.7111
Расчетная t -статистика для р 0	^0	13.4386	11.3365
Изменение социально-экономических условий инновационной деятельности	Р 1	-1.4252	0.0775
Расчетная t -статистика для р 1	t pl	1.0734	0.3926
Изменение научно-технического потенциала	Р 2	1.8070	0.1452
Расчетная t -статистика для р 2	t P2	1.2301	0.4324
Изменение инновационной деятельности	Р з	-1.7907	-0.1321
Расчетная t -статистика для р 3	^3	1.8590	2.0185
Изменение качества инновационной политики	Р 4	0.3162	0.1373
Расчетная t -статистика для р 4	t p4	0.4394	1.9119
Критическая точка распределения Стьюдента	^ к	1.9908	1.9921
F -критерий Фишера расчетный	(Ч	1.9378	1.4182
Критическое значение распределения Фишера	Фк ) р	2.4889	2.4937
Составлено по таблице 3.

Рис. 3. Оценка достоверности интегральных оценок социально-экономических объектов

1. Привязка комплексной оценки к результирующему показателю на который будем оказывать воздействие посредством изменения интегральной оценки
2.1. Однофакторный дисперсионный анализ	2.2. Корреляционный анализ	2.3. Множественная линейная регрессия	2.4. Логистическая регрессия изменения динамики	2.5. Другие методы статистического анализа и обработки данных

Источник: составлено авторами.

друга, так и в совокупности, дополняя и подтверждая соответствующие статистические гипотезы, либо же указывая на необходимость проведения дополнительных исследований (рис. 3) .

В соответствии с рисунком 3 вначале должен быть определен устойчивый стабильный показатель, который фиксируется в статистических отчетностях без каких-либо изменений и потенциально будет использоваться в дальнейшем. Затем необходимо установить между ним и интегральной оценкой связь (как показано в работе, это может быть сделано посредством дисперсионного, корреляционного и регрессионного анализа), которая позволит дать оценку достоверности разработанной интегральной методики. Чем больше статистических тестов будет применено к оценке взаимосвязи между результирующей метрикой и интегральной и чем больше совпадений по итогу окажется между ними, тем более устойчивыми и достоверными будут выводы, которые могут быть получены при сопоставлении социально-экономических объектов, оцениваемых по интегральным методикам.

Немаловажными в решении данной проблемы также выступают методы, предназначенные для снижения размерности, количества иссле-

дуемых процессов и явлений. В итоговую модель следует включать существенные факторы, что показано на примере рассмотренных в статье методик.

Также стоить отметить подход, связанный с использованием узкопрофильных эконометрических моделей, учитывающих пространственное расположение исследуемых объектов; временной лаг проявления какого-либо события; нелинейный характер протекания процесса и др. Данные проблемы и вопросы не являются тривиальными и в большей мере применимы к метрикам и показателям, которые могут быть однозначно сняты с интересующего нас исследуемого объекта. В случае оценок на манер интегральных или комплексных подобный подход навряд ли будет иметь успех, так как включает вещи, которые в различном проявлении протекают независимо друг от друга и будут только путать исследователя при попытках математического моделирования.

Материалы публикации могут быть использованы специалистами в области научнотехнологического развития, инновационной деятельности и продвижения технологий, а также учеными и исследователями, занимающимися статистической обработкой и анализом данных.