К обоснованию метода устойчивого оценивания посредством неравенства Чебышёва

Предисловие

Использование методов устойчивого оценивания необходимо при наличии в потоке наблюдений сильно отклоняющихся наблюдений, шумов, ошибок и прочих помех, что в действительности и бывает в информационноизмерительных системах управления технологическими процессами, при обработке экономической информации и т. п.. Обычный путь построения метода: фундаментальное обоснование, построение алгоритма оценивания и его проверка вычислительным экспериментом, что и описано ниже.

1.    Обоснование метода оценивания

Как известно, по неравенству Чебышёва, для случайной величины Х: Q ^ R, определенной на вероятностном пространстве ( Q , F , P ), с конечным математическим ожиданием ц и конечной дисперсией с ² имеет место соотношение

P (X - ц| >  k c ) <  1/k². (1)

То есть, в 1-м приближении, фильтрация сильно отклоняющихся наблюдений сводится к тому, что при известной дисперсии выборки

(или ее оценке) можно оценить верхнюю границу вероятности сильно отклоняющихся наблюдений и присвоить им эту оценку в качестве веса (меньшего единицы), наблюдениям же, для которых величина правой части неравенства (1) больше единицы, оставить единичный вес.

Следующий шаг – несколько искусственный прием.

Сумма вероятностей наблюдений в выборке равна 1, поэтому веса, полученные на предыдущем шаге, следует перенормировать так, чтобы сумма их была единичной. Далее производиь обычное оценивание, использующее веса наблюдений. Но это было бы возможно при некоторой предварительной известной оценке положения ( ц ) и масштаба ( с ), которые позволили бы вычислить веса наблюдений. В качестве таких предварительных оценок (1-го приближения) для ц и с ² подходят обычные (неустойчивые) оценки математического ожидания и дисперсии E(X) и D(X), затем по получении устойчивых оценок организуется итеративная процедура. Исследование ее сходимости – предмет вычислительных экспериментов.

В качестве 1-го приближения для оценки с можно также взять значение точности измерительного инструмента, посредством которого получается выборка наблюдений.

2.    Интерпретация

При другом варианте построения метода используются следующие     рассуждения.

Представим, что каждое наблюдение Х i в выборке (мощностью n) есть некоторая реализация математического ожидания µ , тогда для X 1 и оценки масштаба (например, в виде точности измерительного инструмента) выполним оценивание весов остальных наблюдений, применяя неравенство (1). То есть, если бы математическое ожидание выборки равнялось X₁, то (при некоторой оценке σ ) наибольшая вероятность появления других наблюдений была бы оценена по неравенству (1) и им были бы присвоены соответствующие веса. Поскольку наблюдения в выборке предполагаются независимыми (реализациями случайной величины), то рассуждение это повторяется для всех X_i (i = 1, n ), а веса каждого j-го наблюдения при i-х рассмотрениях суммируемы. Затем веса перенормируются так, чтобы сумма весов равнялась единице. Получается алгоритм взвешивания, подробно описанный ниже. Для 1-го приближения оценки масштаба σ может быть использована как неустойчивая оценка, так и значение точности измерительного эксперимента. Итерационная процедура использует оценки σ , полученные на предыдущем шаге.

В случае применения этой процедуры взвешивания при аналогичных рассуждениях можно предполагать, что разность между любыми двумя наблюдениями из выборки (X_i – X j ) есть некоторая реализация "разброса" наблюдений, тогда оценка масштаба получается независимой от оценки положения:

Ошибка! , где Ошибка! ,

Ошибка! .              (2)

3.    Описание алгоритма

Используя вышеописанную интерпретацию неравенства Чебышёва (1) и подход с использованием функций влияния [2], введем некоторую "взвешивающую" функцию f0, об- g0(x0;x)

функция влияния, f 0 (х 0 ;x)

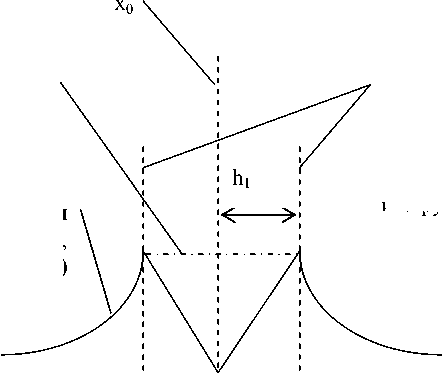
диапазон отклонений в 1-м приближении соответствующей точности измерительного инструмента

Рис. 1. Функция влияния оценки положения,1-е приближение

ладающую свойствами:

• 1)    симметричности¹ 1 ,

• 2)    ограниченности,

• 3)    убывании на бесконечности до 0, см. рис. 1.

Ошибка! , (3) где h 1 интерпретируется как точность измерительного инструмента. Посредством этой функции f 0 определяются веса наблюдений выборки.

Рассуждения обоснования метода интерпретируются далее в терминах подхода с использованием функций влияния.

Для каждого наблюдения выборки X – x_i определяется его вес w_i как сумма влияний f 0 (x i ;x j ) на наблюдение x i наблюдений x j (i ≠ j):

Ошибка! . (4)

Затем для выборки строятся обычные оценки среднего с весовыми коэффициентами.

Ошибка! . (5) Следует отметить, что выражение для стандартного отклонения даёт новую оценку точности измерений h 2 :

Ошибка! . 6) При этом по результатам вычислительных экспериментов, последовательность h i сходится к некоторой величине h₀, являющейся некоторым выражением точности произведенного набора измерений.

Мера же масштаба (рассеяния) выборки, приближенно совпадающая с обычной оценкой стандартного отклонения, есть сумма квадратов разностей наблюдений, умножен-

• ¹    Возможен в общем виде и несимметричный случай.

4.    Вычислительный эксперимент

ных на веса обоих наблюдений, делённая на сумму произведений весов:

Ошибка!, где Ошибка! . (7)

Как вариант "взвешивающей" функции – функция с постоянным в пределах точности измерительного инструмента значением:

Ошибка! .(8)

В m-мерном случае "взвешивающая" функция f₀ есть функция от m-мерных векторов x 1 , x 2, соответствующих наблюдениям выборки (зависящая от расстояния между наблюдениями i и j). При этом корреляции, ковариации, применение регрессионных методов, метода главных компонент обычны для этих методов с весовыми коэффициентами, при вычислении весов указанным выше способом. Это упрощает приложение данного метода устойчивого оценивания к известным методам статистического оценивания в отличие от методов, указанных в работе [2].

Как указано в [2], наиболее сложно выполнять устойчивое оценивание в малых выборках, поэтому ограничиваемся для иллюстрации метода выборкой минимально возможного объема в 3 наблюдения.

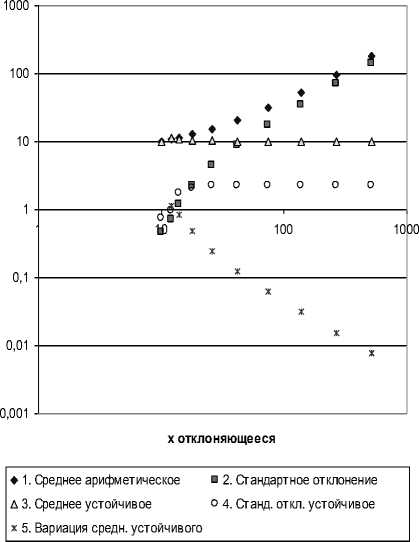
В качестве примера вычислительного эксперимента проведены вычисления для трёхточечной выборки (9, 11, х), одно из наблюдений которой, х, является возмущающим, отклоняющимся значением, х ∈ [10, с.522]. Начальное приближение h₁=1.

Результаты вычислений отображены на рис. 2. При увеличении значения отклоняющегося наблюдения значения устойчивого среднего и устойчивого стандартного отклонения не возрастают, в отличие от обычных среднего арифметического и стандартного отклонения, и более того, отклоняющееся наблюдение при увеличении его отклонения перестает оказывать влияние на устойчивые оценки. При отклонениях х>30, M u ≈ 10.

Таким образом, видно, что алгоритм более устойчив, нежели медиана (считающаяся самой устойчивой оценкой положения), дававшая бы в этом случае оценку положения 11.

мость метода подтверждена вычислительными экспериментами; к тому же его применение вкупе со стандартными методами оценивания, с добавлением к ним лишь процедуры "взвешивания" наблюдений, весьма и весьма удобно, в отличие от других, гораздо более громоздких робастных оценок. Область приложения методов устойчивого оценивания многообразна, например, в системах обработки зашумленных результатов наблюдений [3], а также при оценке экономических параметров (как то: определение средней зарплаты при сильной дифференциации и несимметричности доходов и т. п.).