К оценке деформативности решетчатой пластинки глаза

Задачи биомеханики глаза в последние годы весьма интенсивно использовались в практической офтальмологии. Среди важных проблем биомеханики глаза отметим задачи, связанные с оценкой факторов, влияющих на внутриглазное давление, в частности, на деформирование решетчатой пластинки, и факторов, его определяющих. Как известно, задний отдел склеры в месте выхода зрительного нерва очень тонок и имеет множество отверстий в области, занятой решетчатой пластинкой. Изучение ее характеристик имеет существенное значение в патогенезе глаукомного повреждения зрительного нерва, поскольку ряд авторов устанавливает анатомические отличия между решетчатой пластинкой здорового и больного глаз [11, 14]. Одной из первых публикаций, посвященных решетчатой пластинке, является работа [10]. В ней решетчатая пластинка моделировалась однородной изотропной пластинкой, где была реализована попытка учета влияния растягивающих усилий, действующих со стороны склеры на прогиб пластинки. В современных работах принято моделировать объект неоднородной пластинкой. Учет неоднородности решетчатой пластинки принципиально

Ватульян Александр Ованесович, д.ф.-м.н., профессор, заведующий кафедрой теории упругости, Ростов-на-Дону

Потетюнко Ольга Андреевна, студентка кафедры теории упругости, Ростов-на-Дону важен, поскольку она оказывает существенное влияние на ее деформирование при повышении внутриглазного давления [6]. Это и другие свойства решетчатой пластинки и их влияние на деформирование наиболее полно изучены в работах [4, 9]. Однако следует отметить, что модели однослойных пластинок не позволяют учесть некоторые экспериментальные данные; например, тот факт, что атрофия зрительного нерва при повышении внутриглазного давления возникает на «наружном слое» [1].

Немаловажной задачей является поиск точки перегиба решетчатой пластинки [5]. Это связано с тем, что она состоит из нескольких листов соединительной ткани и наиболее сильные деформации претерпевает последний слой. В работе [15] отмечено, что при деформации пластинки возникает точка перегиба, характеризующая смену участков выпуклости и вогнутости, исследование местоположения которой играет важную роль в практической диагностике глаукомы; в этой же работе предложен экспериментальный метод нахождения координаты точки перегиба.

Как отмечалось выше, решетчатая пластинка представляет собой задний отдел склеры, ослабленный множеством отверстий. По различным данным [7, 12], число отверстий около 700 и занимают они примерно 2/3 площади всей пластинки. От центра к краю решетчатая пластинка становится более разреженной, т.е. эффективный модуль упругости в плоскости изотропии убывает в этом направлении, и при моделировании переменности модуля упругости в [2] использован убывающий экспоненциальный закон.

В настоящий момент при исследованиях деформирования решетчатой пластинки принято моделировать ее как круглую или же близкую к круглой пластинку переменной жесткости с жестко заделанным краем [6]. Вместе с тем отметим, что непосредственный контакт решетчатой пластинки со склерой требует учета упругого закрепления, что позволит более точно оценивать прогиб и в рамках такой модели с большей точностью восстанавливать значение внутриглазного давления. На это указывает работа [13], в которой авторы установили, что деформация пластинки в значительной степени зависит от модулей упругости и толщины склеры. Моделирование упругого опирания пластинки может быть осуществлено различными способами. Так, в [3] была рассмотрена задача о колебаниях неоднородной упруго опертой пластинки с двумя коэффициентами жесткости, в рамках такой модели была решена задача восстановления этих коэффициентов по известному прогибу или по двум резонансным частотам. Подходы, предложенные в этой работе, могут оказаться полезными при совершенствовании моделей деформирования решетчатой пластинки.

В настоящей статье рассмотрено несколько задач о деформировании круглой упругой пластинки переменной жесткости с различными граничными условиями, в том числе упругого опирания. Считается, что пластинка по краю имеет упругую связь, которая характеризуется двумя коэффициентами в граничных условиях. В осесимметричном случае сформулирована краевая задача для пластинки переменной жесткости при наличии упругого опирания. Для этого на основе вариационного принципа Лагранжа для пластинки был сформулирован и решен численно с помощью метода Ритца ряд вспомогательных задач, не содержащих искомых коэффициентов; получено представление прогиба как дробно-рациональной функции, содержащей искомые параметры, построена система нелинейных алгебраических уравнений, из которой и находятся коэффициенты жесткости заделки. В рамках такой модели также была поставлена и решена задача о восстановлении трех параметров коэффициентов жесткости и распределенной нагрузки, связанной с внутриглазным давлением. Проведен ряд вычислительных экспериментов, показавший хорошую точность реконструкции параметров. Выяснено, как распределение жесткости пластинки влияет на точки ее перегиба. В рамках исследования также была рассмотрена задача об оценке влияния коэффициентов жесткости на реконструкцию давления; установлено, что неучет упругости заделки ведет к существенным ошибкам реконструкции в его определении.

Постановка задачи

Рассмотрим равновесие решетчатой пластинки, которая моделируется круглой упругой изотропной пластинкой радиусом а переменной жесткости, на нее действует распределенная нагрузка q . Будем считать, что край пластинки упруго оперт, моделируется двумя упругими связями на краю. Безразмерный лагранжиан для такой пластинки в случае установившихся колебаний построен в [3], а в рассматриваемом статическом случае соответствующий функционал Лагранжа имеет вид

М²   Г W '( Г ) 1 ²       Г W '( Г ) W "( Г )

> rdr - J qw ( r ) rdr +

F ( w ) = 2 J f ( r )“ w (r ) ] + [ r J ⁺ П r

D ( ar ) D о ¹ = f ( r ) , D o = max D ( £ ), w = aW , g 1 = C 1 a ² D o ^{- 1} , g 2 = C 2 D o ^{- 1} , q ^{( r} ) = q o ^{( ar} ) a "³, ^r = ^ a ^{- 1},

D (У - цилиндрическая жесткость; w = w ( £ ) - функция поперечного прогиба пластинки; a - радиус пластинки, 0 < ^ <  a ; fr ) - безразмерная жесткость;

w ( r ) - прогиб; C 1 , C ₂- коэффициенты жесткости заделки; V - коэффициент Пуассона.

Из (1) путем варьирования функционала и приравнивания к нулю коэффициентов при независимых вариациях можно получить уравнение равновесия

Lw = ( fw "r )• - ( fr ¹ w •)’ + v [ ( fw ')" - ( fw ")' ] = qr                    (2)

и соответствующие граничные условия

M 1 w = { - ( fw" r )' + fr ¹ w '-v ( fw ')' +v fw "+ g 1 w }| 1 = M⁰ w + g 1 w 1 = 0, M ₂ w = { fw" r + v fw ’+ g ₂ w *}| = 1 = M 2 w + g ₂ w '| 1 = 0.

Отметим, что граничные условия содержат два параметра, характеризующие влияние склеры на деформирование решетчатой пластинки.

Для нахождения прогиба w использован метод Ритца. Функция прогиба представляется в виде линейной комбинации

N

w ^{( r} ) = Е c k ф k ^{( r} ) ,                                    ⁽⁴⁾

к = 1

где ck - некоторые коэффициенты; фк - базисные функции вида фk(r) = r2(к-1), к = 1,2...N .

После подстановки (4) в функционал (1) и нахождения его стационарного значения построена система линейных алгебраических уравнений относительно неизвестных коэффициентов разложения с_к , решая которую находим функцию прогиба согласно (4).

Таблица 1

Положение точки перегиба в зависимости от закона изменения жесткости

f ( r )	r *
1	0,5799
1 - 0,5 r2	0,6399
e ~r	0,6499
1 + cos r	0,5999
e — r 2	0,6599

Как отмечено во введении, важной задачей в диагностике глаукомы является нахождение точек, в которых происходит изменение характера выпуклости, – точек перегиба. Для их нахождения необходимо выяснить структуру прогиба согласно (4) и далее найти точки перегиба. В табл. 1 показано, как искомая точка перегиба r _* движется в зависимости от задания закона изменения жесткости fr ). Серия расчетов показала, что достаточно выбрать N = 8, поскольку дальнейшее увеличение вносит несущественные поправки и усложняет расчеты. Для простоты принято q = 1. Коэффициент Пуассона считается равным 0,4.

В настоящее время считается, что экспоненциальный закон наиболее адекватно описывает реальную жесткость решетчатой пластинки.

Для того чтобы убедиться в достоверности результатов расчетов прогиба пластинки, сравним численные значения прогибов для однородной пластинки с известными аналитическими результатами [8] в случае жесткой заделки (см. табл. 2).

В табл. 3 приведены прогибы в наборе точек для различных законов жесткости. Принималось, что g 1 = g 2 = 5 - 10⁴. Видно, что наибольшие прогибы реализуются при экспоненциальном распределении жесткости.

Таблица 2

Сравнение прогибов при жестком закреплении

r	Точное решение [15]	Метод Ритца
		g 1 = g 2 = 104	g 1 = g 2 = 5 - 104	g 1 = g 2 = 105
0	0,015625	0,015681	0,015636	0,015631
0,25	0,013733	0,013789	0,013744	0,013738
0,5	0,008789	0,008844	0,008799	0,008795
0,75	0,002991	0,003043	0,003001	0,002996
0,95	0,000149	0,000199	0,000159	0,000153

Таблица 3

r	f ( r ) = 1	f ( r ) = 1 - 0,5 r2	f ( r ) = e "  r
0	0,015636	0,021941	0,029942
0,25	0,013744	0,019285	0,026318
0,5	0,008799	0,012346	0,016847
0,75	0,003001	0,004208	0,005739
0,95	0,000159	0,000219	0,000294

Прогибы для различных законов жесткости

В табл. 4 приведено сравнение прогибов в центре однородной пластинки ( f ( r ) = 1), вычисленных с помощью метод Ритца, с данными, имеющимися в литературе [4], причем в [4] заделка считалась жесткой.

Если оценить влияние параметров g ₁ и g ₂ на деформативность пластины, то оказывается, что значительно более выражено влияние g ₁ , чем g ₂ .

Сравнение прогибов однородной пластины

Таблица 4

Параметры заделки	Давление q , мм рт. ст.	Прогиб, 10 - 2 мм	Прогиб [5], 10 - 2 мм	Расхождение, %
g 1 = g 2 = 10	15	0,8904	0,86	3,53
g 1 = g 2 = 10 4	15	0,8954	0,86	4,12
g 1 = g 2 = 103	15	0,9461	0,86	10,01
g 1 = 10 3 , g 2 = 10 - 2	15	0,9465	0,86	10,05
g 1 = 5 - 10 4 , g 2 = 7 - 10 4	30	1,7819	1,73	2,99
g 1 = 8 - 10 3 , g 2 = 2 - 10 2	30	1,7937	1,73	3,68
g 1 = 9 - 10 2 , g 2 = 2 - 10 4	30	1,9046	1,73	10,09
g 1 = 9 - 10 5 , g 2 = 3 - 10 4	40	2,3730	2,30	3,17
g 1 = g 2 = 103	40	2,5228	2,30	9,69
g 1 = g 2 = 105	40	2,3743	2,30	3,23

Задача о реконструкции параметров жесткости

Поставим обратную задачу об определении параметров g ₁ и g ₂ по известному прогибу w ( r_k ) = X _k , k = 1,2... m . Стандартный способ определения параметров состоит в использовании метода наименьших квадратов. В то же время отметим, что возможен иной подход к решению этой проблемы, для чего сформулируем три вспомогательные задачи:

1 0 Lw o = rq , w oI r = 1 = 0, w o 'l r = 1 = 0;

• 2 0    Lw _x = 0, M° w 1 |r = 1 = 0 , M 2 w 1 r = 1 = 1;                                              (6)

• 3 0    LW 2 = 0, M 2 W 2 |r = 1 = 1, W 2 |r = 1 = 0.

Оператор L определен при выводе уравнения равновесия, а M10 , M 20 – операторы из краевых условий (3), не содержащие g1 и g2 . Прогиб будем искать в виде линейной комбинации описанных выше вспомогательных задач w = w0 + C1 w1 + C2 w2.

В динамическом случае в [3] установлено, что прогиб в точках ri есть дробнорациональная функция от параметров g1 и g2 вида w (r) = a 0g 1 g 2 + aig 1 + a 0g 2 + a3

i     a 0 g 1 g 2 + a1 g 1 + a 2 g 2 + 1 ’ где a0, a1 , a2 , a0i , a1i , a2i , a3i – известные числовые коэффициенты. В статическом случае прогиб будет иметь аналогичный вид. Таким образом, для решения задачи об определении параметров достаточно знать прогиб в двух точках пластины, тогда для определения параметров имеет место система b0 g 1 g 2 + b11 g 1 + b 2 g 2 + b3 = 0, b02 g 1 g 2 + b12 g 1 + Ь 22 g 2 + Ь32 = 0-

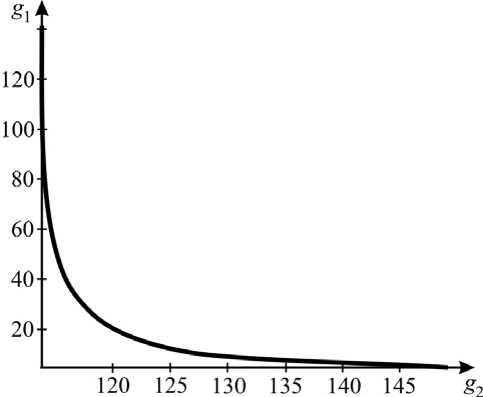
Рис. 1.    Область параметров, обеспечивающих погрешность реконструкции g1 , g2 менее 10 % (выше сплошной линии)

Таблица 5

Коэффициенты из разложения (4)

	10			20			30
	N = 3	N = 5	N = 7	N = 3	N = 5	N = 7	N = 3	N = 5	N = 7
с 1	0,0109	0,0110	0,0110	0,3111	0,3142	0,3143	–0,2740	–0,2742	–0,2742
с 2	–0,0035	–0,0037	–0,0037	–0,0447	–0,0541	–0,0549	0,0372	0,0399	0,0401
с	0,0010	0,0017	0,0018	0,0075	0,0195	0,0223	–0,0075	–0,0142	–0,0149
с 4		–0,0008	–0,0010		–0,0066	–0,0111		0,0054	0,0074
с 5		0,0002	0,0006		0,0012	0,0051		–0,0012	–0,0037
с 6			–0,0002			–0,0017			0,0014
с 7			0,0001			0,0003			–0,0003

Каждое из уравнений системы (8) в пространстве параметров задает ветви гипербол с осями, параллельными осям координат, и такая система, вообще говоря, имеет два решения. Проблема выбора единственного решения разрешается дополнительным требованием положительности искомых параметров. Вычислительные эксперименты показали хорошую степень точности реконструкции при значениях параметров, показанных на рис. 1, причем при восстановлении g ₂ погрешность на порядок выше, чем при восстановлении g ₁ . Это объясняется тем, что g ₂ вносит меньший вклад в значение прогиба (что можно увидеть также из табл.4).

В табл. 5 приведем значения коэффициентов c_k из разложения (4) для вспомогательных задач (6).

С ростом N коэффициенты убывают, что свидетельствует о корректности вспомогательных задач и устойчивости вычислительной схемы.

Задача о реконструкции трех параметров

В рамках предложенной модели также можно поставить задачу об определении не только параметров g ₁ , g ₂ , но и нагрузки q , моделирующей уровень внутриглазного давления. При решении такой задачи необходимо знать прогиб в трех точках w ( r_k ) q = ^ _k , к = 1,2,3 - Тогда на основе представления прогиба будем иметь систему трех нелинейных уравнений вида

q ^{( b} о ¹ g i g 2 + ^b 11 g i + ^b 2 ¹ g 2 + ^b 31 ) = ^b 4 ¹ ,

q ^{( b} о ² g 1 g 2 + ^b 1 ² g 1 + ^b 2 ² g 2 + ^b 3 ^{2 )} = ^b'L                             ⁽⁹⁾

'3                  '3            '3             '3          '3

q ^{( b} 0 g 1 g 2 + ^b 1 g 1 + ^b 2 g 2 + ^b 3 ) = ^b 4 •

Видно, что выражения в левых частях пропорциональны q , и (9) приводится к системе вида (8) путем деления первого уравнения на второе и второго – на третье, что позволяет исключить q . Из полученной системы вида (8) находятся g ₁ , g ₂ , аналогично предыдущему пункту, а далее полученные значения подставляются в одно из уравнений (9), откуда и находится q . Сравнение восстановленных данных с исходными показало достаточную степень точности алгоритма.

Исследование влияния упругости заделки

Как отмечалось выше, в большинстве работ решетчатая пластинка считается жестко защемленной по краю. Предлагаемая в настоящей работе модель с упругим опиранием позволяет сформулировать задачу об оценке ошибки при определении давления, которую влечет за собой неучет упругости заделки, т.е. если решетчатая пластина считается жестко защемленной ( g 1 , g 2 ^да ). Для моделирования такой ситуации сначала заделка считается упругой, фиксируются значения g ₁ , g ₂ , q , находится прогиб w ( r ) при заданных параметрах. Далее заделка полагалась жесткой и по найденному w ( r ) восстанавливалось значение q _* . Сравнение изначально заданного q и восстановленного q _* позволяет оценить степень влияния коэффициентов g ₁ , g ₂ на определение давления. В табл. 6 ниже приведены погрешности реконструкции давления в различных точках.

Из таблицы видно, что неучет влияния упругости при небольших значениях параметров g ₁ , g ₂ приводит к значительной погрешности при реконструкции давления. По мере приближения к краю пластинки точек измерения погрешность увеличивается, так как увеличивается влияние упругости заделки, что также видно из рис. 2.

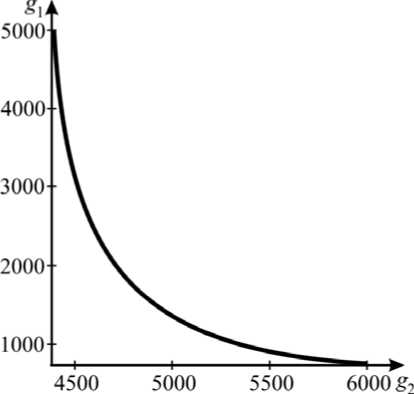
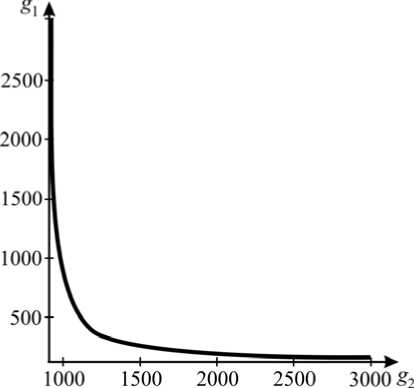
Таблица 6

Оценка погрешности при восстановлении нагрузки

Заданные параметры Погрешность восстановления q в точке a /8, % Погрешность восстановления q в точке a /2, % Погрешность восстановления q в точке 4a /5, % g1 = g 2 = 105 0,04 0,06 0,26 g 1 = g 2 = 5-104 0,07 0,12 0,52 g1 = g 2 = 104 0,37 0,62 2,58 g1 = g2 = 5-103 0,74 1,24 5,16 g1 = g 2 = 103 3,71 6,22 25,80 g1 = g 2 = 5-102 7,42 12,44 51,60 а                                             б

Рис. 2. Область параметров, обеспечивающих погрешность реконструкции давления менее 10 % (выше сплошной линии): я - в точке 4 a /5, f ( r ) = 1 + r ²;

б - в точке a /2 , f ( r ) = 1 + r ²

Заключение

В работе были представлены результаты решения нескольких типов задач. Была решена прямая задача: получены прогибы и найдены точки перегиба пластинки. Также решена обратная задача: проведена реконструкция двух (жесткостей закрепления), трех (жесткостей закрепления и нагрузки) параметров, а также показано, как неучет упругости закрепления приводит к ошибкам реконструкции параметра нагружения.