К оценке долговечности длинномерных гибких труб

Надежность и безопасность технологических работ с использованием гибких труб (колтюбинг ( coiled tubing ) – технология и готовое изделие – намотанная на барабан труба) играют важнейшую роль как в процессе бурения скважин, так и при проведении геофизических исследований, ремонтных и других работ. Возможные при этом аварии сопряжены с большими экономическими и материальными потерями, таким образом, минимизация риска ставит перед производителями гибких труб актуальную и весьма непростую задачу. В этой ситуации оценка числа рабочих циклов, которое может выдержать гибкая труба до разрушения, чрезвычайно важна как для производителя – при назначении гарантийного срока службы изделия – так и для потребителя колтюбинга, в целях успешного и безопасного проведения работ на скважине.

Сложные условия эксплуатации и высокие нагрузки на гибкие насосно-компрессорные трубы в процессе работы предъявляют весьма жесткие требования к их механическим характеристи- кам. Ситуация осложняется тем, что для выполнения задач, возложенных на колтюбинг, материал одновременно должен обладать двумя противоречивыми свойствами – прочностью и пластичностью.

Рис 1. Схема деформирования материала в опасной точке опасного сечения трубы в типичном технологическом цикле:

1-2 – размотка с барабана; 2-3 – изгиб на направляющей; 3-4 – выпрямление после направляющей; 4-5 – приложение эксплуатационных нагрузок; 5-6 – технологический процесс; 6-7 – снятие нагрузок; 7-8 – изгиб на направляющей; 8-9 – выпрямление после направляющей; 9-10 – намотка на барабан

В течение одного типового технологического цикла (спускоподъемной операции – СПО) отдельные области трубы несколько раз подвергается неупругому знакопеременному деформированию: во время спуска – при размотке трубы с барабана, изгибе на направляющей дуге, выпрямлении в инжекторе и далее при погружении в скважину и подаче давления; во время подъема – при прохождении через направляющую, выпрямлении после направляющей и, наконец, при намотке на барабан. При этом в опасном сечении трубы в разные моменты вре- мени реализуется как «жесткое» (ограниченное по деформации), так и «мягкое» (ограниченное по напряжению) нагружение. История изменения деформации в одной из точек такого сечения для одного технологического цикла показана на рис. 1.

Расчетный метод оценки ресурса реализован в ряде зарубежных программных продуктов, таких как Cerberus, FACT , Pegasus, CTLIFE и ряде других. Применяемые в этих пакетах расчетные схемы основаны на анализе большого объема статистических данных и представляют собой эмпирические зависимости, относящиеся к конкретному типоразмеру и классу прочности колтюбинга. Заметим, что во всех названных пакетах в качестве механических характеристик материала используются показатели прочности и пластичности, отвечающие однократному статическому нагружению, причем в детерминированном виде; ими же определяется класс прочности трубы.

Недостатком таких программных пакетов является также недостаточно корректный учет технологии конкретного производства: влияния остаточных напряжений в зоне сварных швов (продольных и поперечных), вида поперечных швов, особенностей термообработки, начального упрочнения (наклепа) и других технологических факторов. Игнорируется характер поведения металла при циклическом нагружении: как известно, циклически упрочняющиеся и разупроч-няющиеся материалы нецелесообразно использовать для изготовления колтюбинга, так как в этом случае вряд ли удастся обеспечить приемлемое количество циклов до момента разрушения - образования макротрещины. В этих условиях единственным приемлемым вариантом являются циклически стабильные и циклически стабилизирующиеся стали. Характер стабилизации (в сторону упрочнения или разупрочнения) также оказывает заметное влияние на поля напряжений и деформаций в представительных точках трубы в процессе ее работы.

К сожалению, держатели таких пакетов неохотно раскрывают их содержание. Не исключено, что некоторыми из них предусматривается эмпирического типа коррекция указанных обстоятельств, опирающаяся на полученные в ходе многочисленных испытаний на специальных стендах опытные данные [1]. Однако в ходе подобной коррекции необходимо иметь в виду, что в полноразмерном трубчатом образце при изгибе на стенде реализуется неоднородное напряженное состояние, поэтому для перехода от усилия, прикладываемого к объекту, и перемещения (или его кривизны) к напряжению и деформации в выбранной точке необходима соответствующая математическая модель конструкции, учитывающая неупругий характер работы материала, влияние градиента напряжений и т.д. В то же время на специальной машине, предназначенной для проведения механических испытаний в условиях растяжения - сжатия, стандартный образец работает в условиях однородного напряженного состояния, таким образом, в результате получают непосредственно свойства материала - как деформационные, так и прочностные.

Со всей очевидность напрашивается вывод, что экспериментальный метод оценки долговечности объекта является наиболее адекватным, однако реализация его непосредственно на скважине вряд ли возможна.

Как следует из рис. 1, основную часть программы нагружения в СПО составляют циклы повторного изгиба. С учетом этого обстоятельства целесообразно проведение стендовых эквивалентных ресурсных испытаний в условиях, например, знакопеременного поперечного изгиба с последующим пересчетом экспериментально полученного числа циклов до разрушения на долговечность реального изделия в условиях реальной эксплуатации по критерию равенства накопленного повреждения. Такой подход практикуется в передовых отраслях машиностроения - таких, как авиация, ракетно-космическая техника, производство ядерных реакторов и некоторых других [2].

В настоящей работе представлена разработанная на кафедре «Динамика и прочность машин» Южно-Уральского государственного университета методика оценки ресурса, базирующаяся на использовании циклических деформационных и прочностных характеристик материала, расчете кинетики напряженно-деформированного состояния объекта в представительных точках и модели накопления повреждения кинетического типа [3, 4].

Количество спускоподъемных операций, представляющее количественную меру ресурса, находили, как уже было сказано, путем подсчета повреждения - скалярной неубывающей величины ю , характеризующей степень дефектности (поврежденности) материала в данный момент времени. Достижение параметром ю_х критической величины ю с соответствует моменту разрушения

Брылкин А.В., Буксбаум В.Б., Колесников К.И., Порошин В.Б., Усова М.В.

(образованию макротрещины). Согласно гипотезе линейного суммирования повреждения в деформационной трактовке

<ю = to + ю = юс предполагается, что усталостное повреждение ю связано со знакопеременным пластическим течением материала [4]:

∆ ε _p                ∆ ε _p

Д ю = j D p Е^, * d E _p * + j D p E m * d E _p * ,

0                       0

где Е р - пластическая деформация; Де _р - размах пластической деформации в цикле; Е р* - изменение пластической деформации с момента последнего реверса процесса деформирования (изменения знака скорости деформации); m , D p ,D _p - постоянные материала.

В рассматриваемых условиях последнее выражение сводится к известной формуле Мэнсона-Кофина, если принять ю с = 1. Квазистатическое повреждение to s определяется односторонне накопленной деформацией:

нак εp ю$ = —, εf где Ef - ресурс пластичности материала.

Таким образом, исходными данными для расчета текущего повреждения и в итоге оценки долговечности являются результаты расчета кинетики напряженно-деформированного состояния в ряде представительных (обычно, наиболее нагруженных) точек. Последний производили с привлечением обобщенного принципа подобия [3].

Модельный технологический цикл (СПОМ) включал три полных знакопостоянных (отнуле-вых) цикла изгиба в режиме жесткого нагружения (один - с кривизной, соответствующей радиусу барабана, остальные два - радиусу направляющей дуги). Расчеты показывают, что стабилизация процесса деформирования в рамках принятой модели материала происходит уже во втором технологическом цикле. Таким образом, повреждение в опасных точках, накопленное к моменту разрушения, составит ю^ = юл + NССПО Дю, где ю1 - повреждение в первом нестабильном технологическом цикле; Аю - повреждение во всех остальных СПОМ; NССПО - долговечность, выраженная в циклах СПОМ.

При нагружении по такой программе квазистатическое повреждение ю _s отсутствует, поскольку одностороннего накопления деформации не происходит.

В стендовых испытаниях на установке ОАО «Уралтрубмаш» (рис. 2) было реализовано жесткое знакопеременное симметричное нагружение отрезка трубы достаточной длины по следующей программе: изгиб до максимально допустимой установкой деформации, распрямление в исходное положение, изгиб в противоположном направлении до равной по модулю деформации обратного знака, распрямление. Следует отметить, что данная схема нагружения является более жесткой (в смысле повреждения), чем в случае модельного СПОМ.

Для расчета накопленного повреждения необходимо располагать циклическими деформационными (параметры кривой циклического деформирования и циклической кривой, циклический предел пропорциональности) и прочностными (предел текучести, временное сопротивление, истинное сопротивление разрыву, а также параметры кривой малоцикловой усталости) характеристиками стали, которые получают экспериментально.

В связи с отсутствием необходимых опытных данных требуемые величины были определены приближенно - по характеристикам статической прочности и пластичности. Для описания кривой усталости использовали «уравнение универсальных наклонов» Мэнсона-Лэнджера, аппроксимацию кривой статического деформирования производили по Рамбергу-Осгуду степенной зависимостью вида где о = oexp(e) - истинное напряжение; е, ep -полная и пластическая логарифмическая деформации; e = ln(1 +е), ep = ln(1 +Ep), при Ep < 10 % можно считать, что ep =Ep (максимальное отличие Серия «Математика. Механика. Физика», выпуск 7                             77

не превышает 0,5 %); K и n – коэффициент прочности и показатель упрочнения (константы мате- риала в данных условиях, порядок их определения изложен в учебном пособии [5]).

Полная деформация трубы при изгибе

..    (Db К её по некоторому радиусу I -2- I определя- ется известными соотношениями:

у     1       D_b D + d

.

£ = — , У = -D, Р = — + р     2        2    4

Здесь D и d – наружный и внутренний диаметры трубы; D b – диаметр элемента, задающего кривизну (диаметр барабана или направляющей дуги); ρ – радиус кривизны нейтральной линии; ε – полная деформация трубы.

Таким образом, зная параметры функции, описывающей статическую кривую,

К£Р решением уравнения —— + £ = £ можно Е найти неупругую составляющую полной деформации.

ПУЛЫ УПРАВЛЕНИЯ

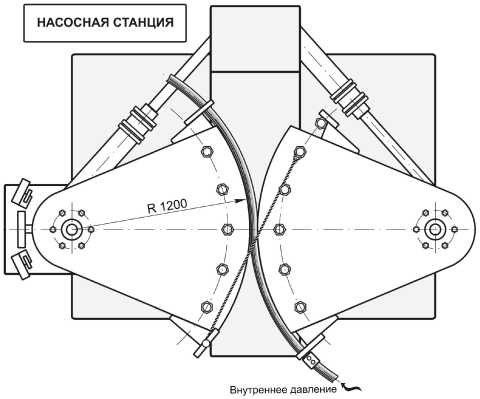
Рис. 2. Схема испытательного стенда

ОАО «Уралтрубмаш», реализующего циклический знакопеременный изгиб трубчатого образца, вырезанного из исследуемой трубы

При повторном нагружении кривая циклического деформирования – кривая деформирования в цикле – в соответствии с принципом Мазинга представляет «удвоенную» начальную кривую:

—    (£

n

12 7

. K ( £р

, соответственно £ = 2— —-

E

_X n

■ ⁺ £ р .

7

Брылкин А.В., Буксбаум В.Б.,                                          К оценке долговечности

Колесников К.И., Порошин В.Б., Усова М.В.                           длинномерных гибких труб

(рис. 5). Полученную зависимость с учетом объективного разброса результатов допустимо аппроксимировать линейной функцией вида

N ^С _f ^ПО = 0,66 N f + 113.

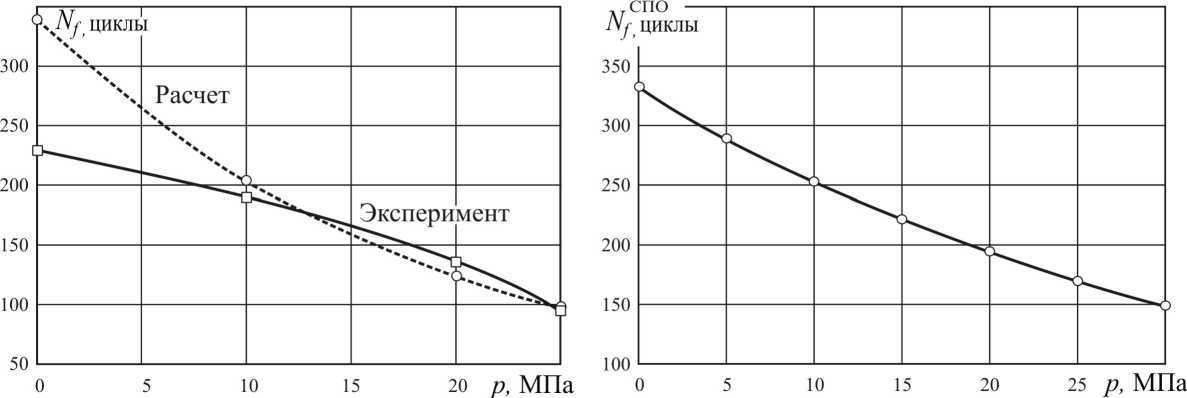
Рис. 4. Зависимость количества модельных технологических циклов (СПО М )

в зависимости от величины внутреннего давления от величины внутреннего давления

Рис. 3. Значения расчетной и полученной в результате стендовых испытаний долговечности

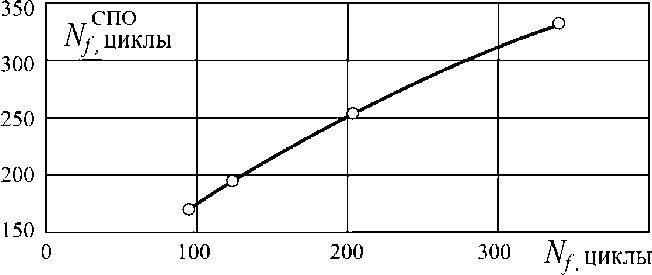
Рис. 5. Связь числа модельных технологических циклов (СПО М ) и долговечности трубы-образца в стендовых испытаниях

Авторы отдают себе отчет в том, что даже такой, основанный на эквивалентных испытаниях реального объекта подход к оценке ресурса колтюбинга носит приближенный характер, поскольку учесть всевозможные случайные повреждения поверхности гибкой трубы в процессе эксплуатации: ее искривление или застревание в скважине и тому подобные обстоятельства, практически невозможно. Поэтому неотъемлемым элементом обеспечения надежности гибких длинномерных насосно-компрессорных труб является систематический мониторинг состояния колтюбинга.