К оценке коэффициента гидравлического сопротивления в гладких трубах

Автор: Лепихин Анатолий Павлович

Журнал: Вычислительная механика сплошных сред @journal-icmm

Статья в выпуске: 4 т.8, 2015 года.

Бесплатный доступ

Выполнен сопоставительный анализ наиболее распространённых аналитических соотношений, по которым находится коэффициент гидравлического сопротивления в гладких трубах. Предложена новая простая формула, содержащая минимальное число эмпирических параметров и позволяющая в явном виде рассчитывать данный коэффициент. Проведена оценка эффективности предложенного выражения и осуществлено сравнение результатов вычислений на его основе с имеющимися в литературе данными, следующими из материалов детальных экспериментов, выполненных в Принстонском и Орегонском университетах и опубликованных в 2004 году. Расчётные и экспериментальные величины анализировались на основе средних, медианных и максимальных абсолютных значений их относительных отклонений. Осуществлённые расчёты показали, что, несмотря на близкие между собой результаты, которые дают указанные эксперименты, построенные исходя из них расчётные соотношения существенно различаются. Так, если рассматривать в качестве критерия эффективности расчётных соотношений средние арифметические значения или медианы относительных отклонений, то наилучшее совпадение с экспериментальными данными Орегонского эксперимента обеспечивает представление, предложенное Г. Баренблаттом. Предлагаемое же в настоящей работе соотношение для оценки коэффициента даёт несколько большие отклонения от этих результатов. Но, в то же время, при сопоставлении с Принстонским экспериментом вводимая формула обеспечивает наименьшие отклонения как по средним и медианным, так и по максимальным значениям абсолютных отклонений среди всех протестированных расчётных соотношений.

Еще

Коэффициент гидравлического сопротивления, гладкие трубы

Короткий адрес: https://sciup.org/14320780

IDR: 14320780 | DOI: 10.7242/1999-6691/2015.8.4.31

Текст научной статьи К оценке коэффициента гидравлического сопротивления в гладких трубах

При решении широкого круга задач вычислительной гидродинамики принципиальное значение имеет корректность введения в постановку задач коэффициентов гидравлического сопротивления [1]. Соотношения для их расчёта должны, с одной стороны, обеспечивать минимальность отклонений от экспериментальных данных в максимально широком диапазоне значений числа Рейнольдса, а с другой стороны, — использовать минимум вычислительных ресурсов. В связи с этим актуальным является получение новых простых соотношений, удовлетворяющих указанным требованиям.

Исследование коэффициента гидравлического сопротивления имеет длительную историю [2, 3]. Обычно он задаётся следующим образом:

Х = -D ■ (dP/dx)/((V2) -р ■ V2), где D — диаметр трубы; dP/dx — перепад давления на единицу длины трубы; р — плотность жидкости; V — осреднённая по сечению трубы скорость течения.

Как правило, коэффициент гидравлического сопротивления рассматривается в виде функции числа Рейнольдса. Существенные трудности при его определении возникают даже в случае гидравлически гладких труб. Если для ламинарных потоков в гладких трубах из зависимости Гагена–Пуазейля формально следует, что

X (Re) = 64/Re ,

где Re — глобальное число Рейнольдса, то для турбулентных потоков ситуация значительно сложнее. Первое наиболее известное соотношение для нахождения коэффициента гидравлического сопротивления (коэффициента Дарси) при турбулентных течениях в гладких трубах было предложено Блазиусом [4] еще в 1913 году:

X bi (Re)=

0,3164 Re 0,25

В работе [5] сделана попытка обоснования данного соотношения, исходя из схемы Колмогорова диссипации турбулентной энергии.

Выполненные Никурадзе под руководством Прандтля классические эксперименты по изучению динамики потоков в трубах позволили получить более точные оценки для большего диапазона чисел Re [6]:

X P (Re) =-----

( 1,95 •

lg ( ^Re T^ P T )

0,55 ) 2

Формула (3) весьма близка к представлению, предложенному Кольбруком [7]:

X C (Re)= 1,3225

( in

^f 2,51

Re, /X

В то же время, согласно уточнённому в [8] соотношению, ориентированному на большие значения числа Re , имеем

-2

X _z (Re) =

0,813 • in ( Re^JX Z ) - 0,241 -

(Re-X. f

На сегодняшний день наиболее полными и детально проработанными оценками коэффициента гидравлического сопротивления считаются те [9], что получены в ходе экспериментов, выполненных в Орегоне и Принстоне [10, 11]. Несмотря на принципиальное различие экспериментальных установок, значения коэффициента в зонах перекрывающихся значений числа Рейнольдса оказались весьма близки друг к другу (Рис. 1).

Согласно полуэмпирическим оценкам на основе экспериментов [10, 11], осуществлённым в [11], функциональная зависимость коэффициента гидравлического сопротивления от числа Рейнольдса выглядит как

X mck (Re) = [ 0,839 • in ( Re ^ ) - 0,537]Л (6)

Исследовательской группой Баренблатта [12] было получено следующее соотношение для определения коэффициента в виде функции числа Рейнольдса:

X B (Re) \( Re )8' '-<-»•

e3/2 (V3 + a(Re))

a = ( 32 )

in ( Re )

e — основание натурального логарифма.

где y ⁽ Re ) 2 ^a(Re) a ( Re )( 1 ₊ a ( Re ))( 2 + a ( Re ))

Калибровка коэффициентов данной модели выполнялась на основе экспериментальных данных [6].

В то же время анализ доступных материалов упомянутых экспериментов дал основание предложить весьма простое соотношение, позволяющее в явном виде находить величину коэффициента гидравлического сопротивления и обеспечивающее хорошее согласование его расчётных и опытных значений:

X L (Re ) =

2 ■ e

(In(Re ))

Зависимости коэффициента гидравлического сопротивления от числа Рейнольдса, как экспериментальные [10, 11], так и расчётные, получающиеся из аналитических выражений (2)–(6), (8), представлены на рисунке 1 и в таблицах 1 и 2. Все вычисления производились с использованием математического пакета Mathcad 15.

Как видно из рисунка 1, соотношения (2)–(6), (8) обеспечивают хорошее соответствие экспериментальным данным [8, 9]; исключение составляет выражение (2) — модель Блазиуса, при Re > 10 5 . Она корректна лишь при Re < 8 ■ 10 4 , что отмечалось еще Прандтлем [4].

Выполненные автором настоящей работы вычисления показали, что значения, найденные по формуле (3), хорошо согласуются со значениями, установленными по (4); так же соотносятся между собой результаты вычислений по (5) и (6). Расчёты и эксперименты можно сопоставить более детально, если обратиться к таблицам 1–4.

Мерой различия наблюдаемых в эксперименте и расчётных значений служили относительные отклонения: AX i = |X _эксп -X i _расч| /Х _эксп . В таблицах 3 и 4 представлены их значения AX i , соответствующие коэффициенту гидравлического сопротивления X i , найденному по соотношениям (4), (5), (7), (8); при оценке используются материалы экспериментов в Орегоне (Табл. 3) и Принстоне (Табл. 4).

Если в качестве показателя эффективности рассматриваемых расчётных соотношений принять средние арифметические значения или медианы абсолютных значений относительных отклонений AX _i , то наилучшую согласованность с экспериментальными данными, принадлежащими группе из Орегона, обеспечивает соотношение (7), предложенное Баренблаттом [12], при этом среднее значение равняется AX B = 2,2040 ■ IO ^-2 , а значение медианы — 1,904. Соотношение же (8) характеризуется средним отклонением AX L = 2,5268■Ю ^-2 , а медиана, соответственно, составляет 2,214. Однако (7) даёт большее по сравнению с (8) максимальное значение: max | AX B | = 6,903 .

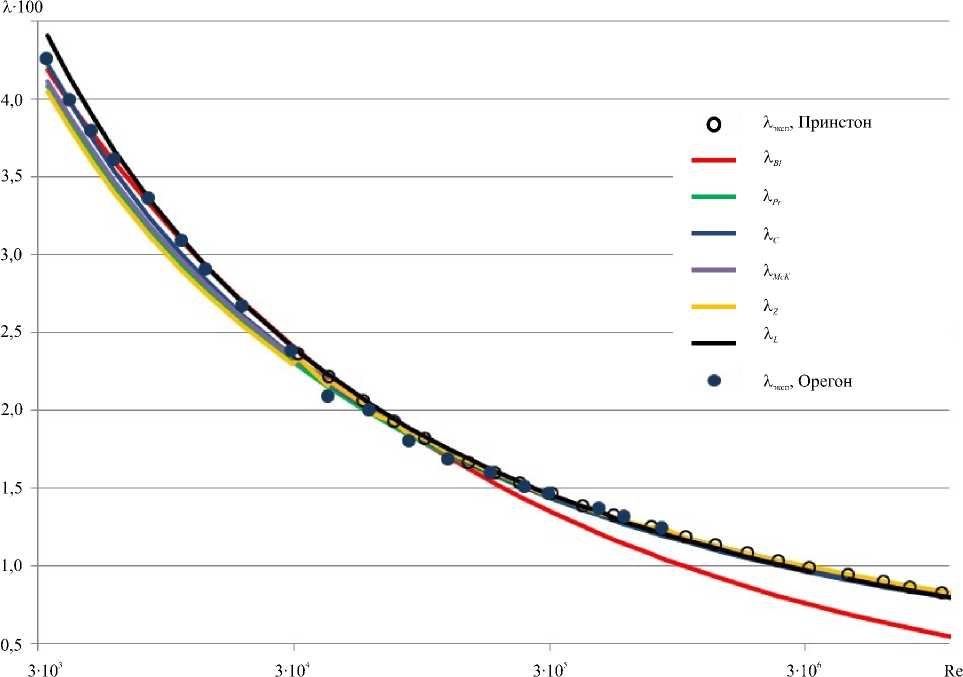
Рис. 1. Зависимости коэффициента гидравлического сопротивления от числа Рейнольдса (Re), согласующиеся с аналитическими соотношениями (2)–(6), (8) и данными экспериментов [8, 9]

Я Я О

ОО

сч

■у

^\ 7

о у

S у

в я я CL Я

сч у

Я r

S я

Cd я о

Я R

CL Ф

Г|

К Я R

§ я о п я я h О CL Я О

зЯ Я Я 1 я f-о

Я Я ^

о о

я я я

1 и

о у

3 а r я

о я

я я

р^

с-1

сч

£ я

я Я я

у 40

-У е о у

о я

’Я

я я

я я cd R

00 ’Я

СИ Я

,6-

"я

S ь

cd CL

о я о

ГС

р^

сч

1—1

S ч

Я"

я я ю

я "я

Г-

Г)

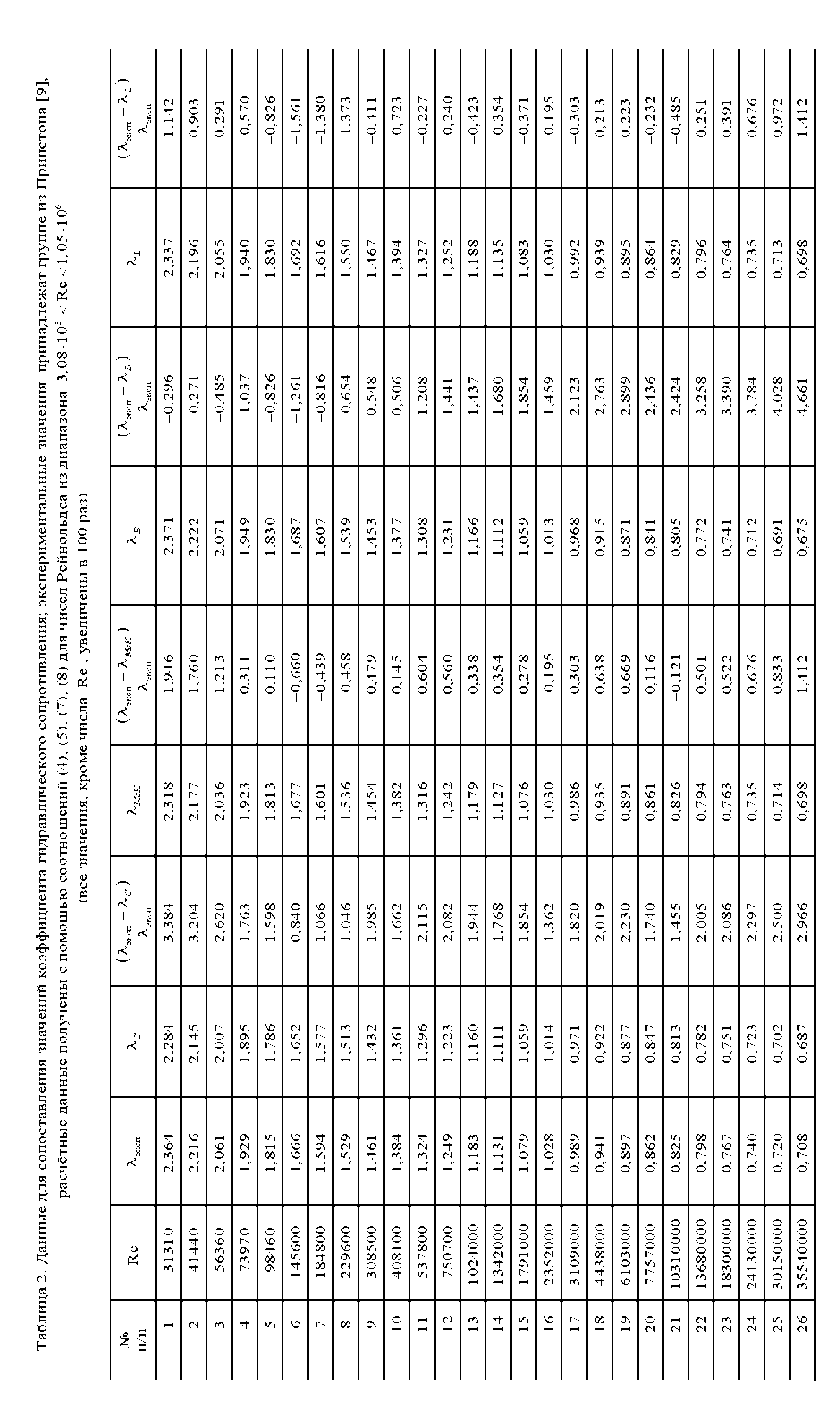
Таблица 3. Характерные значения относительных отклонений ∆λ _i , вычисленные по различным соотношениям для коэффициента гидравлического сопротивления и данным Орегонского эксперимента для диапазона 3,26 ⋅ 10³ < Re < 10⁶ (все значения увеличены в 100 раз)

Расчётные соотношения, используемые для оценки ∆λ _i		Среднеарифметическое значение ∆λ _i	Медиана ∆λ _i	Среднеквадратическое значение σ ∆λ i	max ∆λ _i
Обозначение	Номер формулы	Среднеарифметическое значение ∆λ _i	Медиана ∆λ _i	Среднеквадратическое значение σ ∆λ i	max ∆λ _i
λ _C	(4)	2,9310	3,189	1,5260	5,767
λ McK	(5)	2,3340	2,318	1,2953	4,794
λ B	(7)	2,2040	1,904	1,7970	6,903
λ L	(8)	2,5268	2,214	1,4792	6,420

Таблица 4. Характерные значения относительных отклонений ∆λ _i , вычисленные по различным соотношениям для коэффициента гидравлического сопротивления и данным Принстонского эксперимента для диапазона 3,13 ⋅ 10⁴ < Re < 3,5 ⋅ 10⁷ (все значения увеличены в 100 раз)

Расчётные соотношения, используемые для оценки ∆λ _i		Среднеарифметическое значение ∆λ _i	Медиана ∆λ _i	Среднеквадратическое значение σ ∆λ i	max ∆λ _i
Обозначение	Номер формулы	Среднеарифметическое значение ∆λ _i	Медиана ∆λ _i	Среднеквадратическое значение σ ∆λ i	max ∆λ _i
^λ C	(4)	1,9780	1,964	0,6762	3,384
λ McK	(5)	0,6016	0,490	0,4825	1,946
λ B	(7)	1,8280	1,450	1,2510	4,661
λ L	(8)	0,6210	0,417	0,4370	1,561

При сопоставлении результатов вычислений по авторской формуле с материалами Принстонского эксперимента оказывается, что среди всех рассмотренных расчётных формул предлагаемое в настоящей работе соотношение (8) обеспечивает наиболее низкие значения как медианных величин ( АХ L ~ 0,417 - 10 -2 ), так и показателя максимальных значений отклонений — max |АХ L | ~ 1,561 - 10 -2 . Минимальные среднеарифметические значения АХ i имеют место при использовании соотношения (5), введённого в [9], но показатель максимального отклонения получается при этом следующим: max ∆λ _Z = 1, 946 ⋅ 10 ^-2 . Если оценивать эффективность рассматриваемых расчётных соотношений по показателю max ∆λ _i , то в сопоставлении с экспериментальными данными из Принстона наибольшие отклонения даёт соотношение (7): max ∆λ _B = 4, 661 ⋅ 10 ^-2 . Следует заметить, что (7) приводит к самым максимальным отклонениям также и при сравнении с экспериментальными данными, полученными в Орегоне.

Выводы

Предложено новое простое аналитическое соотношение, позволяющее в явном виде рассчитывать коэффициент гидравлического сопротивления для турбулентных течений вблизи гидравлически гладких поверхностей. Проведено сопоставление значений, полученных на основе формулы, введённой автором настоящей работы, со значениями, найденными по известным из литературных источников соотношениям для этого коэффициента, а также с данными Орегонского и Принстонского экспериментов, опубликованными в 2004 году. Показано, что хотя при описании результатов Орегонского эксперимента новое выражение несколько уступает некоторым из всех рассмотренных аналитических выражений по величине показателя max ∆λ _L , однако среди всех оно наилучшим образом согласуется с данными Принстонского эксперимента.

Список литературы К оценке коэффициента гидравлического сопротивления в гладких трубах

Козелков А.С., Курулин В.В., Пучкова О.Л., Лашкин С.В. Моделирование турбулентных течений с использованием алгебраической модели рейнольдсовых напряжений с универсальными пристеночными функциями//Вычисл. мех. сплош. сред. -2014. -Т. 7, № 1. -C. 40-51.
Бисвас А.К. Человек и вода. -Л.: Гидрометеоиздат, 1975. -288 с.
Форхгеймер Ф. Гидравлика. -М.-Л.: ОНТИ НКТП, 1935. -616 с.
Прандтль Л. Гидроаэромеханика. -М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000. -574 с.
Gioia G., Bombardelli F.A. Scaling and similarity in rough channel flows//Phys. Rev. Lett. -2002. -Vol. 88, no. 1. -014501.
Nikuradze J. Gesetzmäßigkeiten der turbulenten Strömung in glatten Rohren//VDI. Forschungsheft. -1932. -No. 356; Рус. пер. в сб.: Проблемы турбулентности/под. ред. М.А. Великанова, Н.Т. Швейковского. -М.-Л.: ОНТИМ. -1936. -С. 75-150.
Colebrook C.F. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe lows//J. of the ICE. -1939. -Vol. 11, no. 4. -P. 133-156.
Zagarola M.V., Smits A.J. Mean-flow scaling of turbulent pipe flow//J. Fluid Mech. -1998. -Vol. 373. -P. 33-79.
Высоцкий Л.И. Рекомендации по использованию формул для коэффициента Дарси при расчете распределения осредненных скоростей//Научный журнал РосНИИПМ. -2014. -№ 4 (16). -С. 204-212.
Swanson C.J., Julian B., Ihas G.G., Donnelly R.J. Pipe flow measurements over a wide range of Reynolds numbers using liquid helium and various gases//J. Fluid Mech. -2002. -Vol. 461. -P. 51-60.
McKeon B.J., Swanson C.J., Zagarola M.V., Donnelly R.J., Smits A.J. Friction factors for smooth pipe flow//J. Fluid Mech. -2004. -Vol. 511. -P. 41-44.
Баренблатт Г.И. Автомодельные явления -анализ размерностей и скейлинг: Учеб. пособие. -Долгопрудный МО: Издательский Дом Интеллект, 2009. -216 с.

Еще

Статья научная