К определению законов распределения моментов образования и разрушения динамических сводов при установившемся режиме истечения зернистых материалов

Известно, что процесс истечения зерновых материалов из выпускных отверстий бункеров сопровождается образованием и разрушением динамических сводов [1]. Эти сводчатые структуры образуются по всей высоте движущегося потока через различные интервалы времени и имеют при этом различные периоды существования. Каждый из возникающих динамических сводов некоторое время выдерживает давление вышележащих слоев сыпучего материала, а затем разрушатся. Следствием этого является нарушение равномерности и увеличения времени протекания процесса выгрузки материала из бункера.

В связи с этим возникает необходимость создания адаптивных математических моделей, позволяющих описывать стохастические процессы образования и разрушения сводчатых структур при установившемся режиме истечения сыпучих материалов с целью получения их количественных характеристик [2].

Для описания стохастического процесса образования и разрушения сводчатых структур при установившемся режиме истечения сыпучих материалов из выпускного отверстия бункера, предположим следующее [3].

• 1.    Вероятность образования одного динамического свода в сечении бункера на высоте Н за малый промежуток времени длиной Δ t равна: λ ⋅ ∆ t + 0( Δ t ), где λ -некоторая постоянная;

• 2.    Вероятность разрушения одного динамического свода в сечении бункера на высоте Н за малый промежуток времени длиной Δ t равна: µ ⋅ ∆ t + 0( Δ t ) , где µ -некоторая постоянная;

• 3.    Стационарность. Каковы бы ни были t ≥ 0 и целое n ≥ 0 , вероятность того, что за промежуток времени ( t , t + t ) будет зафиксировано n моментов образования и разрушения динамических сводов,

• 4.    Ординарность. Вероятности образования и разрушения более одного динамического свода в сечении бункера на высоте Н за малый промежуток времени длиной A t - величина большего порядка малости, чем A t ;

• 5.    Отсутствие последействия. Вероятности образования и разрушения n динамических сводов за промежуток времени ( t ₀, t ₀ + A t ) не зависят от чередования об-

• разования и разрушения динамических сводов до момента t0 . Обозначим через Ео, Е., Е2,....,Еп,...... состояния, при кото

одна и та же для всех t ₀ >  0 . Обозначим эту вероятность через P_n ( t );

рых в бункере существует соответственно 0,1,2,...., п,.... динамических сводов.

С учетом предположений 1, 2, 3, 4 и 5 запишем все возможные переходы из одного состояния в другое за промежуток времени длиной A t .

Дифференциальные линейно-разностные уравнения состояния запишутся в следующем виде:

P (t + A t) = P (t) - (1 -1 - At — ід- At) + P /t) - AAt + P+j (t) • (i +1) д - At + 0(At),            i > 1.

Изменение состояния

Е 0 → Е 0

Е ₀ → Е ₁

Е 1 → Е 0

Е ₁ → Е ₁

Е 1 ^ Е 2

Е ₂ → Е ₂

Вероятность перехода

• 1 - 1 -A t

• λ ⋅ ∆ t

• 1 • д -A t

• 1 — 1 - A t — 1 - д - A t

• λ ⋅ ∆ t

• 1    — 1 - A t — 2 д - A t

Е → Е i - 1

Е → Е_i

Е → Е i + 1

Граф перехода процесса образования и разрушения динамических сводов можно представить следующим образом (рис. 1).

i ⋅ µ ⋅ ∆ t

1 — 1 - A t — i - д - A t λ ⋅ ∆ t

Перенеся налево слагаемое P ( t ) и разделив на ∆ t , получим в левой части соотношение P ( t + A t ) — P ( t ) к A t .

Положив t ^ 0 , получим

P ( t ) = — ( 1 + i - д ) р ( t ) + 1 р — , ( t ) + ( i + 1) д - р + , ,

где i >  1 .

При i = 0 аналогичным образом выводится уравнение р ; ( t ) =— a - p ( t ) + д - P 1 (t ).

Так как в момент t ₀ = 0 перехода от неустановившегося режима истечения к установившемуся все динамические своды в бункере разрушены, то начальным состоянием системы является Е_о , то есть

P (0) = 1, P (0) = 0 при i ^ 0 .

Решим дифференциально-разностное уравнение (1) методом производящих ∞ функций. Положим Ф(z, t) = ^ P (t)z .

Заметим, что

д Ф ( z , t ) ∂ t

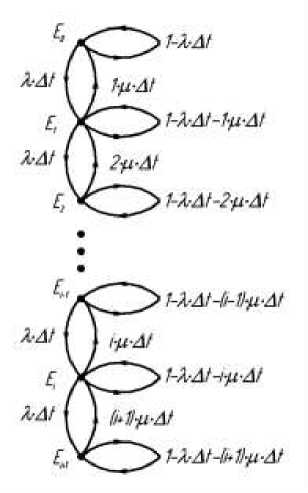
Рис. 1. Граф переходов процесса образования и разрушения динамических сводов и соответствующие вероятности перехода

∞

— £ P ( t)z i

д Ф ( z , t ) ∂ z

∞

= - £ P ( t ) ■ i ■ z .

^z 0

(4)        Умножив обе части (1) на z и про суммировав по i от нуля до бесконечности, получим

∞    ∞∞   ∞∞

£ P ( t) z —- X £ р ( t) z - p £ ip ( t) z + X £ p ₄( t) z + p £ ( i + 1) p ₄( t) z ,

0                       0                  0                   00

откуда дФ (z, t) _ x      .x      дф (z, t)        Г P /.x І-1   Г

—------ЛФ(z, t) - pz— --+ X-z £ Pi-i( t) z  +£(i +-) Pi+i( t) z.

д t                          дz           00

После некоторых преобразований получим дФ (z, t)           ,

------P ^{(1 - z} )

∂ t

Таким образом, мы привели систему дифференциальных линейно-разностных уравнений (1) и (2) к одному дифференци- дФ(z,t) = -X(1 - z) ф (z, t).               (6)

∂z альному уравнению в частных производных (6).

Для решения уравнения (6) рассмотрим соответствующие уравнения Лагранжа:

д t /1 - д z / [ - p (1 - z ) ] - д Ф / [ - X (1 - z )Ф ] ,

где знаменатели пропорциональны коэф- фициентам при

дФ4/, дФя и Ф в урав-/ д t ’  / дz нении (6). Последняя система содержит два независимых уравнения. За первое из них можно принять дt — -дz / p(1 - z).

Это дифференциальное уравнение имеет решение вида exp( -pt )(1 - z) — C1.      (8)

Второе дифференциальное уравнение можно записать так:

д z — p I X-д ФI Ф.

Решение имеет вид                        Общее решение уравнений (7) полу-

Ф(z, t) = C2 exp(2/ p- z),    (9) чим, исключив одну из двух постоянных где C и С2 - некоторые постоянные.         Ci и Сг из уравнений (8) и (9). Таким об разом,

Ф (z , t ) = g ( C i )exp( 2 / p- z )

или Ф ( z , t ) = g ((1 - z)exp(— p t ))exp( 2 / p - z ) .                    (10)

Используя начальные условия (3),

CO находим, что   Ф(z,0) = ^ p (0)z = 1.

Пусть 1 — z = y , тогда

g ⁽ y ) = exp ^{[ ( — 2} / ц ^{)(1 —} y ^{) ]} ,     ⁽¹¹⁾

При произвольном значении t аргументом функции g является (1 — z)exp(pt), поэтому в правой части выражения (11) нужно заменить y на значение этого аргумента. Получим g ((1 — z) exp(—pt)) = exp [— 2 / p(1 — (1 — z) exp(—pt))].

Подставив это выражение в общее решение (10), получим Ф ( z , t ) = exp { — 2 / p (1 — z )(1 — exp( —p t )) } .

Тогда вероятности перехода рассматриваемого процесса примут вид

P n ( t ) = (1/ n !) - ( д ^пФ ( z , t )/ d z n )    z = 0,                        (12)

откуда

P n ( t ) = ( 2 / p ) " - ⁽¹ — ^exp(" ^p t )) ^П exp { — 2 / p (1 — exp( — p t )) } .           (13)

n !

Математическое ожидание и дисперсия числа динамических сводов, имеющихся в бункере в произвольный момент времени, соответственно имеют вид

M ( x ) = 8®^ d z

D ( x ) = b ²( x ) =

z = 1 =-^{- (1 — e}xp^{( —} p t )), p

a ² ф ( z , t ) a z z-

z = 1 +

а ф ( z , t ) a z

z = 1

^'Фд^

>2

z = 1 V

Предельные значения математического ожидания и дисперсии при t ^ 0 соответственно равны:

M ( x ) = D ( x ) = lim ² - (1 — exp( — p t )) = ² .

t >0 p                   p

Итак, среднее число динамических сводов, имеющихся в бункере (как образующихся, так и разрушившихся) в произвольный момент времени t , распределено по показательному закону. Причем это распределение является стационарным и находится в состоянии статического равновесия.

Эксперименты показывают, что частота образования 2 и частота p разрушения динамических сводов для каждого сыпучего материала вполне конкретны и зависят от его физико-механических свойств и конструктивных параметров бункера.

Отметим, что непрерывность и устойчивость истечения наблюдаются, если 2 = p .

Если 2 >  p , то происходит накопление неразрушившихся динамических сводов, приводящих к полному прекращению истечения сыпучих материалов из бункерных устройств.

Выводы

Моменты образования динамических сводов при установившемся режиме истечения сыпучих материалов распределены по закону Пуассона, а промежутки времени между ними распределены по показатель- ному закону. Основными характеристиками законов распределения, описывающими установившийся режимы истечения сыпучих материалов, являются частота образования динамических сводов и частота их разрушения.