К понятию "середина" в аффинных плоскостях

В аффинной плоскости можно ввести понятие середины пары точек различными способами.

Определение 1. Серединой пары точек a, b назовем точку c = ab П (M П L)(N П P ), где M , N , L, P — прямые, удовлетворяющие условиям: M,N I a; L,P I b; M k P ^ ab; N k L ^ M, ab. Обозначение: c = Si[a, b].

Определение 2. Серединой пары точек a, b назовем точку c = e(af П bd) П ab, где e — произвольная точка, не инцидентная прямой ab; d I ae; d = a,e; f I be; df ||ab. Обозначение: c = S ₂ [a, b].

Рис. 2.

(c) 2010 Емельченков Е. П., Шатохин Н. Л.

Определение 3. Точка c называется серединой пары точек a, b, если существует такой перенос т плоскости, что т(a) = c и т(c) = b. Обозначение: c = S3 [a, b].

ττ ------------------------->--------------------------> abc

Рис. 3.

Определение 4. Аффинную плоскость A = { P,L; I, ki будем называть плоскостью с серединой S , если:

• 1)    ( V a, b G P ) ( 3 ! c G P ) c = S [a, b];

• 2)    ( V a, c G P ) ( з ! b G P ) c = S [a, b].

Теорема 1. Аффинная плоскость A с серединой S1 является плоскостью трансляций, удовлетворяющей аксиоме Фано.

C Докажем сначала, что в плоскости A для любой точки o существуют инволютивные коллинеации с центром в этой точке. Для этого рассмотрим преобразование α, которое каждой точке a ставит в соответствие точку a ⁰ такую, что o = Si [a, a ⁰ ].

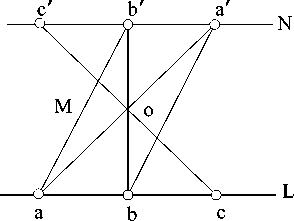
Рис. 4. Преобразование α .

Преобразование сохраняет коллинеарность точек. Действительно, пусть a, b, c I L и b,c - a t a ⁰ (в противном случае доказательство очевидно). Тогда b ⁰ = M П N , где M I a; M ||ba ⁰ ; N I a ⁰ ; N ||ba. Таким образом, точка b ⁰ инцидентна прямой N , проходящей через точку a ⁰ и параллельной прямой L. Аналогично доказывается, что и образ c ⁰ точки c инцидентен прямой N . Следовательно, α — коллинеация. Инволютивность α следует из условия S[a, b] = S[b, a].

Рассмотрим теперь коллинеацию в ° а плоскости A , где а и в — инволютивные коллинеации с центрами a и Si [a, b]. Коллинеация в ° а не имеет неподвижность точек, так как если бы точка c являлась неподвижной, то в(c) = а(c), и, следовательно, пара точек c и a(c) имела бы две различные середины S1[a, b] и a, что противоречит определению 4. Так как, кроме того, (в ° a)(L) | L для любой прямой L плоскости A , то коллинеация в ° а — параллельный перенос, переводящий точку a в точку b. Отсюда следует, что плоскость A является плоскостью трансляций.

В плоскости A диагонали произвольного параллелограмма abcd всегда пересекаются, так как в противном случае пара точек a, b не имела бы середины.

Поэтому A является плоскостью трансляций, удовлетворяющей аксиоме Фано. B

Теорема 2. В аффинной плоскости A с серединой S2 для любой прямой L и направ ления П , L G П , существует инволютивная коллинеация с осью L и направлением П .

C Пусть даны прямая L и направление П, L G П. Рассмотрим отображение а точек плоскости A на себя, переводящее точку a в точку a ⁰ такую, что aa ⁰ G П и S2 [a, a ⁰ ]I L . Инволютивиость отображения а следует из условия S ₂ [a, b] = S ₂ [b, a].

Докажем, что α сохраняет коллинеарность точек. Пусть x, y , z — три точки, инцидентные одной прямой M . Предположим сначала, что M E П и M ^ L. Положив в определении 2 a = x, b = x ⁰ , d = y, e = M П L, получим, что S2 [d, f ] E L и df E П, т. е. что y ' = a(y) = f . Следовательно, образ точки y принадлежит прямой x(M П L). Аналогично показывается, что образ точки z принадлежит этой же прямой. Отсюда вытекает, что прямая M , пересекающая прямую L и не принадлежащая направлению П, переходит в прямую M ' , также пересекающую прямую L. В случае M E П доказательство очевидно. Если же теперь M k L , то, предположив, что точки x ⁰ , y ⁰ , z ⁰ не коллинеарны, получаем, что хотя бы одна из прямых x ⁰ y ⁰ или x ⁰ z ⁰ не параллельна L . Однако этого быть не может, так как в силу доказанного выше и инволютивности отображения α отсюда следует, что M ∦ L .

Таким образом, а является инволютивной коллинеацией с осью L и направлением П.

Замечание 1. Из условия 2) определения 4 следует, что в плоскости с серединой S 2 осевая инволютивная коллинеация однозначно определяется осью и направлением, а в аффинной плоскости с серединой S 1 нейтральная инволютивная коллинеация однозначно определяется центром.

Действительно, пусть α — центральная инволютивная коллинеация с центром o , переводящая точку a в точку a ⁰ , и M , N — две различные прямые, отличные от прямой aa ⁰ . Прямые M и N , очевидно, переходят в прямые M ⁰ и N ⁰ такие, что M k M ⁰ , N k N ⁰ , M ' ; N ⁰ 1 а ' . Точка а пересечения прямых M и N 0 переходит в точку пересечения прямых M ⁰ и N ⁰ . Поэтому точка o инцидентна прямой bb ⁰ . Так как, кроме того, точка o инцидентна прямой аа', то по определению 1 следует, что o = Si [а, а ⁰ ], т. е. для любой инволютивной центральной коллинеации α аффинной плоскости A с серединой S 1 центр коллинеации является серединой пары а и а ( а ).

Для случая осевой коллинеации доказательство аналогично.

Замечание 2. Инволютивную центральную коллинеацию с центром o и инволютивную осевую коллинеацию с осью L и направлением П будем называть также соответственно симметрией с центром в точке o и симметрией с осью L и направлением П.

Теорема 3. Аффинная плоскость A с серединой S 2 является плоскостью с серединой S 1 . При этом

( V a,b E P ) S ₁ [a, b] = S 2 [а, b].

C Пусть a , b — произвольные точки плоскости A , L — прямая, инцидентная точке c = S ₂ [a, b] и не параллельная прямой аЬ. Рассмотрим симметрию а с осью L и направлением П _аь . Выберем на прямой L точку d, отличную от точки S2[a, b]. Тогда прямая M , M k ad ; M I b , пересекающая ось L в точке f , переходит при симметрии α в прямую fa , параллельную прямой bd .

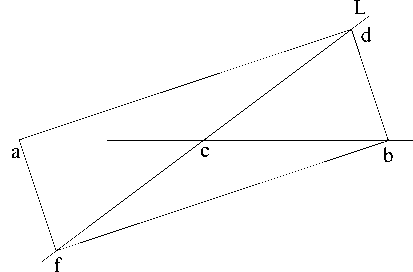
Рис. 5. Симметрия с осью L и направлением Π ab .

Таким образом, точка c является точкой пересечения диагоналей параллелограмма afbd и, следовательно, по определению 1 c = Si [a, b]. Так как выполнение условий 1) и 2) определения 4 для середины S1 следует из их выполнения для середины S2 , то A является аффинной плоскостью с серединой S1 .

Теорема 4. Если A — аффинная плоскость с серединой S1 , в которой выполняется аксиома Фано, то A является плоскостью с серединой S2 и

( V a, b Е P) S _i [a, b] = S2[a, b].

C Известно [1, теорема 5.7.4], что в плоскости трансляций, в которой выполняется аксиома Фано, выполняется аксиома о четвертой гармонической. Поэтому середина S2 удовлетворяет условиям 1) и 2) определения 4, т. е. A является аффинной плоскостью с серединой S2. В силу 3 для любой пары точек а и b Si [a, b] = S2[a, b]. B

Теорема 5. Аффинная плоскость A с серединой S2 , в которой выполняется аксиома Фано, является левоальтернативной плоскостью.

C Из теорем 3 и 1 следует, что A — плоскость трансляций. Из теоремы 2 следует, что для любой прямой L и любого направления П, L Е П, в плоскости существует симметрия а с осью L и направлением П.

Докажем теперь, что композиция двух симметрий α1 и α2 с общей осью L и различными направлениями Щ и П2 соответственно является сдвигом с осью L.

Действительно, выберем прямые M и N так, что M Е Щ, N Е Щ, M П N IL, и рассмотрим параллелограмм oe _i ee ₂ такой, что o = M П N ; e _i 1 M ; e _i = o; e _i e ^ L; e IN; ee ₂ ^ M ; e2 I L (рис. 6). Три точки o, e1 , e2 определяют тернар R, координатизирующий аффинную плоскость A . В этом тернаре точки o, e1 , e2, e имеют соответственно координаты (0, 0), (1, 0), (0,1), (1,1).

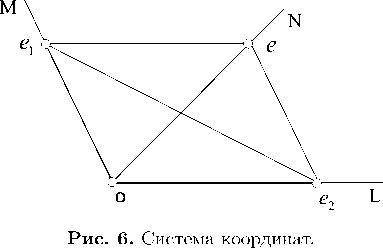
Так как A является плоскостью трансляций, то тернар R удовлетворяет условиям:

• 1)    T (a, b, c) = a x b + c;

• 2)    ( R, + i — абелева группа;

• 3)    a x (b + c) = a x b + a x c.

В плоскости A существует симметрия а с осью N и направлением П _е 1 _е 2 . Так как Si[ei,e2] IN, то a(ei) = 62. Симметрия а действует на точки и прямые плоскости A следующим образом:

(0,1) - (0,0) - x = 0 - (a, a) - x=a - y = b - (a, b) -

* (1,0), (0, 0), y = 0, (a, a), * y = a, x = b, (b, a),

(0,0)         —    (0,0),

^{(1,a)         —    (a}, ¹),

• у = a x x — у = a -¹ x x, (b, a x b) —    (a x b, b).

Так как коллинеация α сохраняет инцидентность точек и прямых, то b = a-1 x (a x b).

Отсюда, положив b = a ^-1 , получаем a ^-1 = a ^-1 = a ^-1 . Следовательно, тернар R обладает свойством:

a ^-1 x (a x b) = b.

Точки (1, 0) и (0,1) при симметрии а переходят соответственно в точки (0,1) и (1, 0). Поэтому прямая у = ( — 1) x x + 1 принадлежит направлению П коллинеации а. Отсюда, в частности, вытекает, что точки (1, — 1) и ( — 1,1) инцидентны прямой у = ( — 1) x x и, следовательно, (0,0) = S2[(1, — 1), ( — 1,1)]. Рассматривая теперь параллелограмм ( — 1, — 1)(1, — 1) (1,1)( — 1,1), по определению 1 получаем, что (0, 0) = S1 [( — 1, — 1), (1,1)]. Поэтому симметрия а2 с осью x = 0 и направлением П у = _х действует на точки и прямые плоскости A следующим образом:

(1, 1)	—	( — 1, — 1),
(x = 0)	—	x = 0,
x=1	—	x = — 1,
у = x + a	—	у = x + a,
(1, 1 + a)	—	( — 1, — 1 + a),
(1, a)	-	( — 1, — 1 — 1 + a),
(0, a)	—	(0, a),
у = a	—	у = (1 + 1) x x + a,
у = x	—	у = x,
(a, a)	—	( — a, — a),
x=a	—	x = — a,
у = b	—	у = (1 + 1) x x + b,
(a, b)	—	( — a, (1 + 1) x ( — a) + b)

Итак, симметрия а2 произвольную точку (x, у) переводит в точку ( — x, (1 + 1) x ( — x) + у). Аналогично доказанному выше получаем, что

(0, 0) = S1 £ (1, 0), ( — 1, 0) ] .

Поэтому симметрия а1 с осью x = 0 и направлением П у =о действует на точки и прямые плоскости A следующим образом:

(—1, 0) — (1, 0), (0, 1) — (0, 1), у = x + 1 — у = (—1) x x + 1, (0, a) — (0, a), у = x + a — у = (—1) x x + a, у = b + a — у = b + a, (b, b + a) — (—b, b + a), т. е. симметрия а1 переводит произвольною точку (x, у) в точку (—x, у).

Композиция а2 о а1 симметрии а1 и а2 точку (x, у) переводит в точку (x, (1 + 1) x ( — x) + у). Отсюда следует, что композиция а ₂ о а1 является сдвигом с осью x = 0.

Итак, композиция двух симметрий с общей осью L и различными направлениями является сдвигом с осью L.

Нетрудно доказать теперь, что в плоскости A для любой прямой L и любых двух точек а и b таких, что ab ^ L, a,b - L, существует сдвиг с осью L, переводящий точку a в точку b. Действительно, пусть α — симметрия с осью L и произвольным направлением, в — симметрия с осью L и направлением П _а ( _а ) ь . Следовательно, композиция в ° а является сдвигом с осью L , переводящим точку a в точку b .

Таким образом, плоскость A является левоальтернативной.

Теорема 6. Аффинная плоскость A , в которой выполняется аксиома Фано, является плоскостью с серединой S 2 тогда и только тогда, когда A — левоальтернативная плоскость.

C Необходимость доказана в теореме 4.

Достаточность. Пусть A — левоальтернативная плоскость, в которой выполняется аксиома Фано. Тогда в этой плоскости выполняется аксиома о четвертой гармонической и поэтому для каждой пары точек a,b середина c = S2[a, b] существует и определена однозначно. Отсюда же следует и выполнение условия 2) определения 4. Таким образом, A является аффинной плоскостью с серединой S 2 . B

Теорема 7. Аффинная плоскость A , в которой выполняется аксиома Фано, тогда и только тогда является плоскостью с серединой S 3 , когда A является левоальтернативной плоскостью.

C Необходимость. Пусть A является плоскостью с серединой S 3 . Тогда из условия 2) определения 4 следует, что для любых двух точек a и b существует перенос τ , переводящий точку a в точку b . Поэтому A является плоскостью трансляций. Так как, кроме того, в A выполняется аксиома Фано, то в плоскости A выполняется аксиома о четвертой гармонической. Отсюда следует, что A является аффинной плоскостью, удовлетворяющей аксиоме Фано, и, следовательно, по теореме 5 A — левоальтернативная плоскость.

Достаточность. Пусть A — левоальтернативная плоскость. Так как в этой плоскости для любой пары точек a и b существует перенос, переводящий точку a в точку b , то условие 2) определения 4 для середины S 3 выполняется.

Докажем теперь, что для произвольной пары точек a и b существует середина S 3 и причем только одна. Введем тернар R так, чтобы точки а и b имели соответственно координаты (0, 0) и (0,1). Тогда перенос т , действующий следующим образом:

(x,y) ^ (x,y +(1 +1)-1), переводит точку (0, 0) в точку (0, (1 + 1)— 1), а точку (0, (1 + 1)-i — в точку (0, (1 +1)-i + (1 + 1)-i) = (0,1). Таким образом, для любой пары точек а и b существует середина S3 [a, b].

Единственность середины c = S3 [a, b] пары точек a, b следует из того, что перенос т , переводящий точки a = (ai, a2) и c = (ci,C2) соответственно в точки c и b = (bi, b2), однозначно определяется условиями:

ci = ai + xo, c2 = a2 + yo, bi = ci + xo, b2 = c2 + yo.

Действительно, из этих условий следует:

bi = ai + xo + xo, bi - a1 = xo + xo,  bi - a1 = (1 + 1) x xo, xo = (1 + 1) x (bi — ai)-

Аналогично получаем: yo = (1 + 1) ¹ x (b2 — a2). Следовательно, перенос т однозначно определяется формулами:

x ⁰ = x + (1 + 1) ¹ x (bi — a1), ^{y 0} = y ^{+ (1 + 1) i x (b}2 ^— a2). >