К расчету динамики гидровинтовых прессов для штамповки с кручением

Работа гидровинтового пресса для штамповки с кручением основана на принципе совместного и одновременного воздействия на заготовку предварительно накопленной на участке разго- на кинетической энергии поступательного и вращательного движений, одновременно совершаемых подвижными частями пресса и энергии давления жидкости, создаваемой в гидроцилиндре.

Область применения гидровинтовых прессов с вращающимся инструментом – изготовление горячештампованных осесимметричных тонкостенных поковок различной формы и размеров (диски, ступицы фланцы, шестерни и др.).

Параметры штамповки с кручением взаимосвязаны с динамическими процессами, происходящими в гидромеханической системе пресса. Анализ динамического состояния гидровинтового пресса с вращающимся инструментом позволит получить данные, необходимые для разработки надежных и работоспособных конструкций прессов такого типа.

На рис. 1 приведена расчетная схема гидровинто-вого пресса для штамповки с кручением [1, 2], которая включает в себя гидроцилиндр 1 с поршнем 2 и штоком 3. Шток 3 через сферический подпятник 4 опирается на винт 5, смонтированный в гайке 6, жестко закрепленной в поперечине 7 станины. Нижний торец винта 5 жестко связан с ползуном 8.

На расчетной схеме приведены следующие условные обозначения: V , ω – скорости линейного и углового перемещений ползуна 8 с винтом 5 в эквивалентном сечении винтового соединения «винт 5 – гайка 6»; Р д , М д – технологическое усилие и момент деформирования; М 1 – момент в винтовом соединении «винт 5 – гайка 6»; М тр , M тп – моменты трения в винтовом соединении «винт 5 – гайка 6» и в сферическом подпятнике;

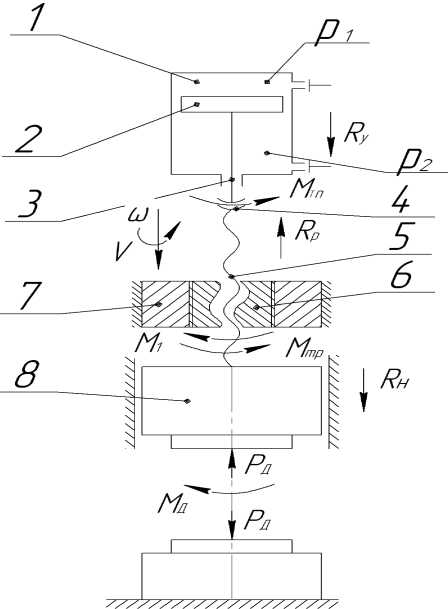
Рис. 1. Расчетная схема

R у , R р , R н – силы трения в уплотнениях гидроцилиндра, в резьбовом соединении и направляющих ползуна.

Жидкость высокого давления р 1 , действуя на поршень 2 гидроцилиндра 1 создает вертикальную гидравлическую силу, действующую через шток 3 и подпятник 4 на винт 5, который, имея несамотормозящую ходовую резьбу, начинает вращаться относительно неподвижной гайки 6 совместно с ползуном 8 и одновременно перемещаться вниз. При этом в винтовом соединении и на ползуне возникают крутящие моменты. В результате за время разгона на участке холостого хода накапливается необходимая кинетическая энергия винтового движения. После контакта вращающегося инструмента с заготовкой ее деформация будет происходить под действием технологического усилия осадки Р д и технологического момента деформирования М д .

Для анализа динамических параметров и определения частот собственных колебаний элементов гидромеханической системы гидровинтового пресса для штамповки с кручением состав- лена динамическая модель (рис. 2).

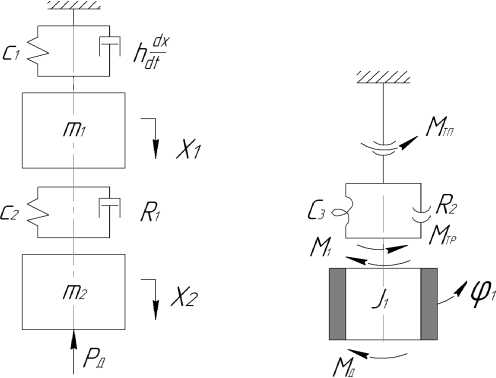
Рис. 2. Динамическая модель

В динамической модели инерционные свойства системы представлены массами, сосредоточенными в определенных точках, и моментами инерции в сечениях, соединенных безынерционными упругодиссипативными или кинематическими связями.

При построении динамических моделей были приняты следующие допущения: взаимодействия распространяются мгновенно; жидкость обладает постоянной вязкостью и нетеплопроводна; температура жидкости установившаяся; сжимаемость жидкости и деформируемость трубопроводов предполагаются пропорциональными приведенным линейным жесткостям; массы жидкости и рабочих частей приводятся к определенным точкам, движение кото- рых анализируется в предположении, что движение жидкости и рабочих частей машины эквивалентно движению этих точек приведения; сопротивления колебательным движениям жидкости пропорциональны скорости, а сопротивления перетеканию под действием разности давлений на концах гидролинии пропорциональны квадрату скорости; станина пресса считается абсолютно жесткой; масса поршня 2 и штока 3 не учитывается; масса винта 5 приведена к массе ползуна 8; зазоры в кинематических парах гидровинтового пресса отсутствуют; коэффициент трения в винтовой паре принимается постоянным.

В динамической модели приняты следующие обозначения: m 1 – масса рабочей жидкости в напорной магистрали, приведенная к ведущему концу упругого звена; m 2 – масса ползуна с винтом и рабочей жидкости в возвратной магистрали, соединенной со сливным баком, приведенная к ведомому концу упругого звена; J 1 – приведенный момент инерции рабочих частей пресса, совершающих вращательное движение.

Приведенные параметры определяются следующими выражениями:

1n ml = p£ flu где p - плотность рабочей жидкости, ft, li - площади сечений и длины прямых участков труб, составляющих рабочую гидролинию;

f          4 п 2

m 2 = (—Ж m + J   ) + m i ] ,

F _П         s ²

где f – площадь напорной трубы; F П – площадь поршня; m – масса поступательно движущихся частей; J – осевой момент инерции вращающихся рабочих частей; s – ход винта;

Трусковский В.И., Киселев В.В.

1k m′ =ρ fl – масса жидкости в сливной гидролинии, где f , l – площади и длины прямых 31

участков труб сливной гидролинии;

s 2

J = m + J .

¹      4 π ²

Взаимодействие масс осуществляется через упругие связи: с 1 – жесткость гидросистемы, приведенная к поршню; с 2 – приведенная линейная жесткость винта 5 и гайки 6; с 3 – приведенная крутильная жесткость винта 5 и гайки 6.

Р _д, М _д – технологическое усилие и момент деформирования; М _тр – суммарный приведенный момент трения в винтовом соединении; М тп – момент трения в сферическом подпятнике; М g – приведенный момент от силы тяжести; h ( dх 1 / dt ) – сила жидкостного трения, где h – коэффициент пропорциональности силы жидкостного трения [3]; R 1 , R 2 , – диссипативные силы сопротивления; х 1 – абсолютное линейное перемещение массы m 1 , вызванное упругой деформацией гидросистемы; х 2 , ϕ 1 – абсолютные линейные и угловое перемещения ползуна 8 с винтом 5 в эквивалентном сечении (сечение, проведенное через центр тяжести эпюры распределения усилия по виткам), соответствующем средней части высоты гайки 6, вызванные упругими деформациями.

Технологическое усилие Р _д, возбуждающее динамические процессы в механической системе гидровинтового пресса и момент деформирования М д , появляется в результате воздействия рабочих частей на поковку, которые можно определить по зависимостям, приведенным в работе [4].

Усилие, возникающее в гидросистеме: P = c 1 x 1 .

Усилие в соединении «винт 5 – гайка 6»:

P2=c3(ϕ1rtgα-x2), где r – средний радиус; α – угол наклона винтовой нарезки винта 5.

Момент в соединении «винт 5 – гайка 6»:

M1= P2rtg(α ± ρ), где ρ – угол трения скольжения в винтовом механизме.

Сила тяжести G подвижных частей создает дополнительный момент:

M = G^s . g    2 π

Сопротивление перетеканию жидкости под действием разности давления на концах гидролинии учитывается согласно принятому допущению как ^Хс 2 , где ^ - приведенный к поршню суммарный коэффициент сопротивления напорной и сливной гидролиний.

Диссипативные силы сопротивления приняты пропорциональными скоростям движения со- c ответствующих масс: Ri = Ц1(х2 - хД R2 = Ц2ф 1. Здесь Ц i = (mi 8 i —)/ п - коэффициент вязкого mi сопротивления в соответствующей упругой связи, где δi – логарифмический декремент затуха-с ния колебаний,   i – парциальная частота колебаний массы mi. Логарифмический декремент mi затухания колебаний можно определить с помощью формулы

δi =ln a1n , a1n+1

где a1n, a1n+1– амплитуды колебаний, соответствующие первому и второму периодам колебаний, определенные экспериментально или заимствованные из статистических данных для известных конструкций.

Начальные условия для принятых координат при t = 0: Х 1 = 0; Х 1 = 0; x ₂ = 0; x ₂ = V ; Ф 1 = 0; ϕ ₂ =ω . V , ω – скорости линейного и углового перемещений ползуна с винтом к моменту начала деформации.

Уравнения движения динамической модели составлялись на основе уравнения Лагранжа второго рода:

d ( дT J д T  дП = Q  ЭФ dt lд qj J д qjд qj    j д qj’ где Т, П– соответственно кинетическая и потенциальная энергия системы; qj – обобщенные координаты; Qj – обобщенные силы; Ф – диссипативная функция системы.

После соответствующих преобразований получается следующая система нелинейных дифференциальных уравнений второго порядка движения масс динамической модели, которые решаются численными методами с использованием вычислительной техники.

dx mx+cx-h 1 +P;

11 11 _dt 1

m 2 x 2 + c 2 (x 2 - x 1 ) - c 1 x 1 -^. x 2 - Р_д - R 1 - S R = 0;

J 1 9 1 + M 1 + M _д + M g - R 2 - M тр sgn (p 1 = 0.

В уравнении движения массы m 2 действия приведенной силы трения в винтовой паре, уплотнениях гидроцилиндра и направляющих ползуна учтены как суммарное их значение Σ R .

Предложенная модель гидровинтового пресса для штамповки с кручением позволяет проводить анализ динамических процессов, происходящих в гидромеханической системе машины на участке рабочего хода.