К расчету квантованных радиально-симметричных ДОЭ

С ростом производительности вычислительной техники широкое распространение приобрел итерационный расчет фазовых дифракционных оптических элементов (ДОЭ) [1,2]. Значительное количество современных технологий изготовления ДОЭ используют аппроксимацию в общем случае непрерывной фазовой функции ДОЭ кусочно-постоянной (квантованной) функцией [3]. Это определяет актуальность построения итерационных процедур расчета квантованных ДОЭ (ДОЭ с квантованной фазовой функцией). Расчет квантованных ДОЭ с помощью итерационных алгоритмов типа Фьенапа [1] затруднен в силу необходимости решения обратной задачи на каждой итерации. Использование стохастических процедур [4] не предполагает необходимости решения обратной задачи, т.е. поиск фазовой функции ДОЭ может осуществляться непосредственно над множеством технологически реализуемых функций , что дает возможность избежать погрешности квантования. Однако построение стохастической процедуры оптимизации реального ДОЭ требует решения большого числа прямых задач, что в общем случае может привести к нереализуемым на практике вычислительным затратам.

Представляется целесообразным рассмотреть применение стохастических процедур оптимизации фазы ДОЭ для случаев, когда решение прямой задачи не требует больших вычислительных затрат (например, в случае радиально-симметричного ДОЭ).

Данная работа посвящена применению известной генетической стохастической процедуры нахождения экстремума функции многих переменных к расчету квантованных ДОЭ, фокусирующих излучение в радиально-симметричные фокальные области.

Оптимизация фазы радиально-симметричного ДОЭ с помощью генетического алгоритма

Генетический алгоритм (ГА) - это итерационный стохастический алгоритм, который работает с набором «индивидов» (популяцией). Каждый индивид представляет собой потенциальное решение задачи. К примеру, в случае расчета радиальносимметричного ДОЭ в качестве отдельного индивида может быть определена фазовая функция ДОЭ ф(r ) Е [0,2 п ] такого вида, что соответствующий микрорельеф

h (r ) = ^( r) X, (2п( n -1)), (1)

где n - показатель преломления материала, X - длина волны излучения, реализуем с помощью имеющихся в наличии исследователя технологических возможностей. В случае наличия технологии изготовления бинарных (двухуровневых) элементов в качестве индивидов целесообразно рассматривать фазовые функции, принимающие в каждой точке одно из двух значений -0 или л (или 2 л и л ). В общем случае расчета ДОЭ с числом уровней квантования M , фазовая функция принимает значение ^ ( r ) е { ( 2 n m / M ) : m е [ 1, M ] } .

Отметим, что если в случае использования «детерминированных» методов [1,2] расчет квантованных ДОЭ с малым числом уровней квантования M ( M =2-8) требует дополнительных усложненных модификаций процедуры расчета, то для стохастической оптимизации уменьшение числа уровней квантования означает уменьшение мощности множества допустимых решений, и, следовательно, снижение вычислительных затрат.

Перед началом работы алгоритма популяция генерируется случайным образом. Затем при помощи некоторого «оценивающего» (целевого) функционала Ф( ф ),каждому индивиду присваивается мера ценности индивида ф в отношении рассматриваемой задачи. Значение Ф( ф ) используется алгоритмом для направления поиска. Конкретный вид функционала в нашем случае определяется приложением ДОЭ. На каждой итерации процедуры численность популяции искусственно увеличивается за счет вводимой определенным образом операции «скрещивания» индивидов исходной популяции. Отобранные лучшие индивиды (в смысле введенного функционала Ф( ф )) используются в качестве исходной популяции для следующей итерации алгоритма.

Было показано [4], что при условии постоянного сохранения лучшего индивида, полученного на предыдущей итерации, и наличии «мутаций», т.е. стохастических изменений значений отсчетов функции ф ( r ) с некоторой заданной вероятностью p , такая процедура обладает сходимостью к глобальному экстремуму Ф( ф ( r )).

Вид функционала Ф(ф(r)) определяется конкретным приложением ДОЭ и его вычисление вовсе не обязательно требует решения прямой задачи теории дифракции. К примеру, если требуется рассчитать элемент, формирующий пучок с заданным модовым распределением, вычисление функционала

Ф( ϕ ( r )) потребует разложения светового поля по

фокального распределения интенсивности (рис. 1)

модам в плоскости непосредственно за оптическим

элементом.

^I 1^,

0,

0 < p < Ri p > Ri

Рассмотрим подробнее построение генетиче-

ской процедуры оптимизации радиально-симметричного квантованного ДОЭ радиуса R . Началь-

ная популяция представляет собой набор N gen сгене-

где R ₁ - радиус фокальной области.

Значение интенсивности I 1 может быть получено из соображения сохранения энергии:

рированных случайным образом одномерных мас-

сивов

I N -1

Ф у / у = 0 -

Каждый массив соответствует одной

2 ^R

I1 = 7? CM J I0 ( r ) rdr ,

R _{1      0}

реализации фазы элемента фт), взятой вдоль его радиуса:

Ф5 = Ф(jА) е {2nm/M} ,

где С _М - константа, описывающая потери энергии, связанные с квантованием фазы по M уровням. Элемент рассчитывается как добавка к внешней сферической линзе.

где А = R/ ( N - 1 ) , R - радиус ДОЭ.

После генерации начальной популяции (популяции «родителей») организуется цикл, в теле которого последовательно выполняются следующие операции:

• -    скрещевание - формирование N chield дополнительных новых индивидов-массивов, значение каждого отсчета которых выбирается как значение соответствующего отсчета случайно выбранного массива – «родителя»;

• -    мутация - стохастическое изменение значений случайно выбранных отсчетов получившихся новых массивов. Значение вероятности мутации p определяет скорость сходимости процедуры;

• -    селекция - определение следующей популяции «родителей» путем выбора N gen лучших (в смысле решаемой задачи) индивидов с помощью вычисления функционала ф ( ф ) для всех N gen + N chield индивидов.

Таким образом, на каждой итерации необходимо найти ( N _gen + N _chield ) значений функционала Ф( ϕ ).

Количество итераций N _it , требуемых для оптимизации фазы ДОЭ в данной работе выбиралось исходя из количества итераций, требуемых для оптимизации тестового функционала, для которого было известно значение глобального экстремума.

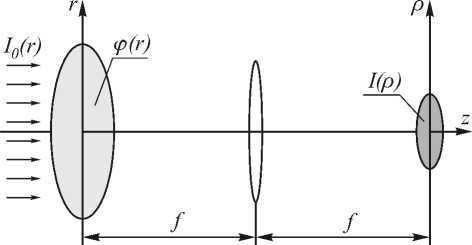
Рис. 1. Постановка задачи синтеза ДОЭ для фокусировки гауссова пучка в круг

В качестве минимизируемого функционала ф ( ф ( r )) логично выбрать невязку:

N - 1                      ₂

ф(ф(r))=EI(А,ф(r))-Ii| ,

I = 0

Выбор функционала для расчета ДОЭ, фокусирующего гауссов пучок в круг

В качестве примера, иллюстрирующего работоспособность предлагаемого подхода, был выбран расчет ДОЭ, фокусирующего гауссов пучок в круг, что объясняется широким спектром потенциальных применений таких элементов.

Выбирая функционал для оптимизации фазы ДОЭ, необходимо учесть следующие требования:

• -    адекватность функционала физической задаче,

• -    минимизация вычислительных затрат, требуемых для его реализации.

Рассмотрим задачу синтеза ДОЭ с радиусом апертуры R для формирования из плоского гауссова пучка

I 0 ( r ) = exp ( ^{- 2} r ²/ ° ² )                           ⁽³⁾

где N 1 = R 1 /A 1 - радиальный размер фокальной области в дифракционных пятнах, А 1 = X f ^IR -размер дифракционного пятна, р 1 = ( 1+0,5) А 1 , I ( р,ф ( r ) ) - фокальное распределение интенсивности, сформированное ДОЭ с фазовой функцией ϕ ( r ).

Комплексная амплитуда светового поля w ( ρ ) в фокальной плоскости линзы может быть представлена как сумма амплитуд, образованных дифракцией плоской волны на кольцеобразной апертуре [2]:

w (А) = E exP (- ji I ° 2) exP (iФ+1)x j=0

^X r + i J 1 ( k P r + i / f )/ А ^- r j J 1 ( k A r j / f )/ А ] ,        ⁽⁷⁾

r j = j А , J 1 ( • ) - Бессель-функция 1^го порядка. Сле-

довательно, значения интенсивности в точках ρ ₁ мо-

гут быть найдены следующим образом:

N-2

I ( p i ) = E exp ( ^- r Ai / ° ² ) exp ( ⁱ Ф j + 1 )

j = 0

x

^x( r j + i J i ( k p l r j + i /f )/ А 1 ^- r j^J i ( k p l r j / f )/ А 1 )l ,          ⁽⁸⁾

или

I(А1 ) =

N-2

E exp (iФj+1) Cj j=0

где

C j = exp ( - ^ 2 + 1 / a ² ) ( r_{y +} i J i ( kpr j + i / f )] p i -

- r j J i ( kprjf}/p ) .

Отметим, что коэффициенты C^l _j не зависят от ϕ ( r ) и могут быть посчитаны до начала работы оптимизационной процедуры.

После завершения работы оптимизационной процедуры подсчитывалось значение энергетической эффективности

R1

e = J I (P) Pd P J Io (r)rdr(11)

и среднеквадратичного отклонения интенсивности от среднего значения I

R1

8 = J[I(p)-I] Pdp ,(

I R_{1 0}

R 1

I = — Ji (p) pdp.(13)

R 1 0

Результаты вычислительного эксперимента

Для постановки вычислительного эксперимента выбирались следующие параметры: длина волны освещающего пучка X=10 , 6 мкм, радиус освещающего пучка о =1,85 мм, фокусное расстояние внешней линзы f =100 мм, радиус апертуры R =3,7 мм, радиус фокальной области R 1 =0,6 мм, число отсчетов фазовой функции N =100, число уровней квантования M =4, количество итераций стохастической процедуры N it =6000. Уменьшение значения функционала невязки Ф с ходом итераций показано на рис. 2. Отметим быстрое уменьшение значения Ф в ходе первых 300-400 итераций алгоритма.

ФА

20-

10-

0    1000 2000 3000 4000

номер итерации

Рис. 2. Зависимость значения невязки от номера итерации

На рис. 3 представлена расчетная интенсивность в фокальной плоскости элемента.

Значение расчетной энергетической эффективности в ходе вычислительного эксперимента составило e =80,3%, значение среднеквадратичного отклонения интенсивности составило 8 =6%.

Таким образом, применение стохастической итерационной процедуры с функционалом (6) позволяет рассчитывать четырехуровневые ДОЭ, фокусирующие гауссов пучок в круг с энергетической эффективностью, близкой к теоретическому пределу (81%), и низким значением среднеквадратичного отклонения. Отметим также небольшие вычислительные затраты, требуемые для реализации расчета элемента, что объясняется простотой вычисления функционала (6) после того, как значения коэффициентов (10) и интенсивности (5) предварительно посчитаны.

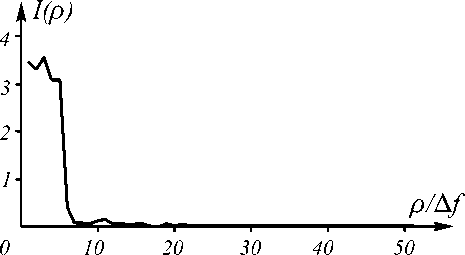
Рис. 3. Радиальное распределение интенсивности, сформированное рассчитанным ДОЭ в фокальной плоскости (результат численного моделирования)

Заключение

В данной работе рассмотрено применение известной генетической итерационной процедуры нахождения экстремума функции многих переменных к расчету квантованного ДОЭ, фокусирующего гауссов пучок в круг.

Приведенные результаты вычислительных экспериментов подтверждают перспективность рассматриваемого подхода, который естественным образом может быть обобщен на случай фокусировки в произвольные радиально-симметричные области.