К расчету пространственного распределения давлений в сжимаемом смазочном слое цилиндропоршневого сопряжения

Введение. Основным узлом трения в двигателе внутреннего сгорания является трибосопряжение цилиндр-поршень, которое влияет на механические потери, определяет тепловое состояние двигателя, угар масла, уровень вибраций и шума. Работоспособность трибосопряжения определяется конфигурацией смазочной зоны, зазорами между поршнем и цилиндром, местом положения пальцевого соединения, профилем юбки поршня. Особенностью работы поршня является и то, что он находится под действием тепловых и силовых факторов в результате чего происходит вспенивание и кавитация смазки, тепловые и силовые деформации, приводящие к изменению зазоров, а иногда и к контакту поверхностей. Все это накладывает особые требования к решению задачи смазки и динамики поршня [1, 2].

В работе рассмотрено течение сжимаемой жидкости в зазоре трибосопряжения цилиндр-поршень при возвратно-поступательном движении профилированного поршня. Рассматриваемая задача имеет практическое приложение, касающееся не только гидродинамической смазки юбки поршня двигателя внутреннего сгорания, но и поршневых насосов, грузопоршневых манометров [3, 4] и других устройств подобного рода.

В основе математической модели лежит структура уравнений теории газовой смазки, причем влияние кавитации и вспенивания учитывается путем введения параметра газосодержания в уравнение состояния. Рассматривается макрогеометрия слоя смазки с возможностью усечения как по круговой, так и по осевой координате боковой поверхности поршня.

Автор считает, что работа цилиндро-поршневого сопряжения (ЦПС) может быть рассмотрена и с точки зрения виброреологических представлений [5]. Основанием для такого рассмотрения служит тот простой факт, что в системе координат, связанной с подвижным поршнем, в процессе движения относительно достаточно длинного цилиндра будут происходить, по сути, периодические изменения зазора, которые отвечают определению вибрации, а значит, и вибрационного сдавливания слоя. Оценка величины этого эффекта требует специальной постановки задачи и в этой работе не проводится.

Математическая модель. Работа ЦПС происходит в очень тяжелых условиях, сопровождаясь вспениванием и кавитацией смазки, которая трудно поддается адекватному описанию и формализации, поэтому здесь используется достаточно универсальный подход, связанный с описанием состояния среды зависимостями следующего вида: плотность среды: р = р1 + а1 (р0 - р1), где р0 и р 1 - плотности газа и жидкости; вязкость среды ц = ц1 + а1 (ц0 - ц1), где ц0 и ц1 - дина мическая вязкость газа и жидкости; зависимость между плотностью и давлением р = кРа3 , где P - давление в слое, а 1, а2 а3 - параметры газосодержания, близкие друг другу и определяемые в каждом конкретном случае по данным эксперимента. При таком подходе газ равномерно распределяется по объему слоя. Представленные зависимости непрерывно описывают состояние среды от несжимаемой жидкости (а = 0) до чистого газа (а = 1) [6-8].

Предполагаем, как и обычно для теории гидродинамической смазки, что среда ньютонов- ская, а ее течение в зазоре является ламинарным и изотермическим ввиду малой толщины слоя, при этом влияние нагрева и вспенивание учитываем через задание определяющей температуры и необходимого значения параметра газосодержания а [7]. В этих условиях и в обозначениях работы [8] безразмерное уравнение для распределения давлений имеет следующий вид:

д д $

2 — а

д ф^{1 + а}

: _ф1 + а д Н

и

^{1 — а} ф ^аv

д

+-- де

' Н ^{2 — а} д ф^{1 + а} - _Н 1 — а _ф 1 + а д Н ) ^ 1 + а д е              д е J

д (ф ^аН ^{1 — а} )

где Л_т = 12 ^v B ² / ( P ₀ hi ₀ ² ), Л_и = 6 ц И ₀ B / ( P ₀ h ₀ ² ), Т ^а = Р ^а Н - искомая функция давлений и зазора [8]. В качестве краевых условий используем условия периодичности для давлений

Т а (^,9) = Т а (^,9 + 2п)(2)

и условия равенства давлений в верхней и нижней части неподвижного цилиндра окружающему (давлению в картере ДВС)

Т а (0,9) = H (0,9).(3)

Выбор начального условия в данном случае некритичен и будет определяться из условия минимума времени численного решения задачи, например

Та (^,9,т = 0) = 1.(4)

Справедливо условие периодичности для функции зазора и давлений по времени, т. е.

Та (^9,т) = Т а(^,9,г +1),(5)

причем, период колебаний определяется временем полуцикла возвратно-поступательного движения профилированных цилиндров. Безразмерная функция зазора определяется, в общем случае, по следующему закону h

H = — = 1 + z ₀ cos 9 + Ф( ^ , 9 ) ,                                                                 (6)

h 0 где Ф(^,9) - функция, определяющая профиль цилиндров. Введены следующие обозначения: ^ = x / B - безразмерная осевая координата; l = L / B - безразмерная длина слоя; h0 - номи- нальный зазор при соосном положении цилиндра и поршня, т = Vt, где v - линейная частота возвратно-поступательного движения поршня.

Алгоритм численного решения задачи. Как упоминалось выше, работа рассматриваемого трибосопряжения происходит в тяжелых условиях, сопровождаясь иногда соударениями ограничивающих слой цилиндров, поэтому метод линеаризации по малому параметру, в качестве которого обычно используется малый эксцентриситет [4, 9, 10], в данном случае нежелателен и предпочтение надо отдать методам решения многомерных задач. Рассмотрим два наиболее приемлемых в данном случае приема линеаризации определяющего уравнения (1).

В первом случае воспользуемся линеаризацией по методу Ньютона, а во втором используем возможности схемной линеаризации задачи, перенося нелинейную часть уравнения на предыдущий временной слой или период колебаний.

В первом варианте линеаризации имеем, в общем случае, следующее итерационное уравнение [11]:

L ^M+1) = L ' ^₀(—n)-L(—n) ,                                                  (7)

где L - производная Фреше от пространственно-временного дифференциального оператора, определяемого уравнением (1), —₀ - начальное приближение для искомой функции давлений ^ “ , —_п и —_п+1 соответственно n и n + 1 итерационное приближение.

По определению [11] имеем:

(8) где L(—) = ^[ (Н^ ^ - Н ^1- «— ¹⁺ « ^) - Л#Н ^1- "у] +

Э С Н² "“ Э^¹⁺ “ ⁺ де ⁽ 1+а де

_Н ^1- «— ¹⁺ «Эе)_Л_шА(—«Н ^1- «).

Обозначим — = Та и подставим выражение (9) в формулу (8), тогда развернутое итерацион- ное уравнение примет вид:

[^Н2-« У@р - (1 + а'Ш¹-»;^ Эн) - ЛЖ+.Н-d +

+ э. |(н^2-" ^ - (1+«)н ^1- «<;^п+1 эн)| ..../,•_»-, ^^-^-(Х + ^Н¹^

Тап.

< Э.||н1 + " 'Н'-^.а-Гп Э,':)| - l(W(10)

Второй вариант линеаризации основан на представлении — ^а приближенным выражением

—а=;1* Т1+а,(11)

где —* - известное решение для функции давлений на предыдущем моменте времени или предыдущем периоде решения задачи. Естественно, что при такой аппроксимационной линеаризации задачи ухудшается устойчивость численной схемы и вопрос о сходимости решения требует спе-

циального исследования.

Обозначим искомую функцию — = Т ^{1 + а} , получим следующее линеаризованное уравнение

д I э?

(Н^ 5^1 - Н1-«—   - Лг ^Ьн1-«у1 +  ( Н ' э- - Н^^) = V 1+а э?         э э^у    " ^*цга       ] эе V 1+а эе          эе/ Э(-^н1 "“ )

■'             _.                                                                                                                         (12)

Воспользовавшись дивергентной формой уравнений (10) и (12) запишем их в соответствии с теоремой Остроградского – Гаусса в интегральной форме

Яд [Q_fd0dT + QedfdT + Л_т^0^^] = Ш_п ^dv ,

Лт

А_шфН ^1-а .

^^^^^е _ш^Н ^1-а ф*1+а

где Q^ и Q_e определяют выражения для расходов по координатам £ и 9 соответственно , причем

поверхность D ограничивает объем Ω , в котором распространяется поток вектора F , порожденно-

го уравнениями (10) и (12). Например, для уравнения (12) имеем:

”2^

^Q kl+a Э^

Н1-а

ФИ)

Qe =

н² "“ э^

1+a эе

-А„-4ЕН1-а^.

^ *1+а

Н1-а

Введем в рассмотрение область определения задачи. На рис. 1 представлена развернутая на плоскости типовая поверхность юбки поршня, на которой заштрихованная область и определяет ее смазочную боковую поверхность. Предусмотрена возможность усечения боковой поверхности поршня. Известно, например, что американские и японские двигатели имеют усечение обычно выше верхнего компрессионного кольца, необходимость которого диктуется требованиями уменьшения угара масла, а для европейского двигателе-строения характерна полная боковая поверхность,

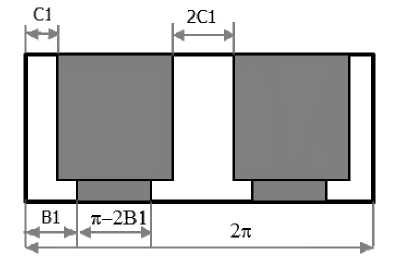
Рис. 1. Развертка боковой поверхности поршня

что связано с экономией топлива и уменьшением температуры критического компрессионного кольца. Эти особенности легко учитываются в рассматриваемом подходе.

В области определения задачи будем использовать следующее сеточное разбиение ш = {(ft. 9m. Tj). (ft±i. 9m±i. Tj) ; ft±1 = ft ± Aft; 9m±i = 9m ± Д9т; ft±i = ft ± 0.5Aft;

9_m± l = 9m± 0.5A9m; t = 1.2.3 .... N; m = 1.2.3 .... M; Tj±i = Tj ± At; j = 1.2.3 ....}       (17)

Будем относить Q^ и Qg к полуцелым узлам сетки, а функции давлений и зазора к целым узлам. В соответствии с идеей балансных методов [12–14] применим уравнение (17) к элементарной ячейке сеточной области:

1^1 I Qf^ 1 — Qf^ i I + (1 — ^1) I Qf^ i — Qf^ i I ( А9_тАт,- + {^2 Qgj i — Qgj i +

14 ?t+2    Ml 1 L M   ?t-21J m j l1L^m+2    m-2-l

+1 - a2Q0m+12j- Q0m - 12j'+1 N фй ^ tj-Atj+1L 0m L (i-Arj N 0m L ^i=Fi,m,J L fi L 0m L tj , (18)

где а₁ и a₂ параметры, позволяющие варьировать интерполяцию сеточных функций.

При численном решении многомерных задач и особенно при включении этих задач в программный комплекс наиболее часто стоит вопрос об экономии расчетного времени, поэтому предпочтение должно быть отдано экономичным алгоритмам и наиболее приемлемым в данном случае, учитывая прямоугольный вид области определения задачи, является метод переменных направлений [12]. Реализация этого метода позволяет получить следующую схему решения зада- чи:

^⁺² —A^A9mAft =

= ^а 1 ^ ^Q f_t+ 1 - ^Q f_t- 1 ²) ^A9 m ^AT j ^{+ (1 —} ^2) ( ^Q em₊1 ^—

Qe^ i ) AftATj —P_t^jAftA9mATj ;    (19)

m~ 2

Qfj+ 1 ¹ ) fvA9mATj — Fi,m,jAfiA9mAтj ; (20)

^⁺¹ —A^A9mAft =

= °"i ( ^Q e ² i ^{— Q} e ² i ) ^Af t ^AT j + ^{(1 —} °' 1 ⁾ (Mv ^{— m+} 2     ^m- 2      ^j           М

^i,m = ^1;

^^jm1 = u ^j+1 при m = M i , m = M ₂ , m = M ₃ , m = M ₄ ; ^t

^im = U при i = 1, i = M 2 , i = M 3 , i = M 4 ,

где

U = ^1U ⁷⁺¹ + (1 - ^1)U ⁷ -

△ t

(  a^^¹ ^\ — Qe^ Mm

] ^-(1 - о/ ⁾⁽ 1 - 02V ^Qe^j.i ^{- Q}e^J_m 1 tmt

4       22

△ 0,

M ₁ = BJAO + 1, M ₂ = ( n - 2 B ₁ )/ AO + 1, M ₃ = ( n + B ₁) /N O + 1;

M ₄ = (2 n - B ₁ )/ A O + 1, N = A₁/ NA + 1, N ₂ = A₂ / A ^ + 1, C₁ = 0;                         (24)

^ = ( W^ или ^ = ( H Xm ■                                      (25)

Конкретизируем полученные разностные схемы. Для схемы с линеаризацией по методу Ньютона при расчете на первом и втором полушаге по времени получаем уравнение трехточечного вида, имеющее второй порядок аппроксимации по координатам f и 0 , причем при а₁ = а₂ = 0,5 получаем также второй порядок аппроксимации по времени. Решение численной задачи на первом полушаге по времени в направлении координаты f является основанием для решения задачи на втором полушаге по времени в направлении координаты 0 . Дале вычисления продолжается уже на следующем временном слое. Решение подобного вида уравнений подробно было рассмотрено и исследовано нами, например, в работах [7, 8] и здесь не приводится.

Рассмотрим линеаризацию вида (11). В соответствии с уравнением (11) и в силу выражения (19), реализующего метод переменных направлений, на первом полушаге по времени можем получить следующее дискретное уравнение:

• 1 /      •    1 /            •    1 /      • 1 /            • 1 /      • 1 /                      • 1 /

__ 14- К __ 1 1/_     __ 11/_ __ 14- V-      — 14- К __ 1 4- 1/_                14- V- ггЛ^ ^{+ /2}W^J+ /2 4- A ^{J +} /2ш ^J+ /2 ,    /2ш ^J+ /2\_( л V+=

° 1^{( A} i + 1, m ~ i + 1, m ^{+ A} j - 1, m ~ j - 1, m ⁺ С 1 , m ~ J , m ) vV ) i , m

+

= -(1 - *2)(A m+1^ i+1, m +A m-1^ J-1, m + Cmm Д Jmm2) - (Лг ) J, m, где Ai( m )±1 = ^^O ^Al [H 2a +H 2(-a±1 ] + (-1) [±Hi( m )±1 ± (-1)Hi( m ) ] 2 Н1("а>±1 j;

A _{z ±} 1 = A± 1 ± (-0,5)A , ■ V ■ a ■ At ■ AO ■ h J - f / T * ±+ “ ;

₌ ^AtAO ( ^AtA^ )J ^0,5 Г 2 -a 2- a 1. Г„ ,„   11_Н1- « L

C i ( m ) A ^ ( A O J[1 + a L^H i ( m ) ^+H i ( m ) + 1 J ⁺ (^Н i ( m ) + 1 ^+Н i ( m ) J 2 ^Н i ( m ) J

_ ^AtAO ( ^AtA ^ )J ^0,5 F_H 2 - a , „2 - « ЪГ„           1 1_Н1 - “ L

A ^ ( A O J[1 + a L^{H 1 ( m} ) ^+H J ( m ) - 1 J ⁺ L^{H 1 ( m} ) ^{+H 1 ( m ) - 1} J 2 ^{Н 1 ( m} )^;

Аналогично уравнению (24) строится уравнение для расчета искомой функции давления на втором полушаге по времени.

Реализация численной схемы и некоторые результаты расчетов. Несколько слов об устойчивости метода переменных направлений. В работе [12] доказывается устойчивость метода переменных направлений по начальным данным и правой части для линейного двумерного уравнения в прямоугольнике, при этом предполагается, что пространственно-дифференциальные конечно-разностные операторы уравнений положительные и самосопряженные. Можно видеть, что выводы работы [12] соответствует и данной задаче. Однако обеспечить устойчивость и сходимость численной схемы (26) можно только при определенном выборе шагов пространственновременной сетки.

В частности, трехточечный вид конечно-разностного уравнения (26) позволяет провести решение соответствующих ему систем линейных алгебраических уравнений на каждом полушаге по времени методом немонотонной прогонкой. Условия устойчивости прогонки могут быть нарушены из-за наличия в коэффициентах уравнений аддитивной составляющей, содержащей параметр сжимаемости Л_у среды:

Α i ± 1 =Α i ± 1 ± ( - 0,5) Λ υ ⋅ V ⋅α⋅∆τ⋅∆θ⋅Η ¹ i ±^- 1 ^α ;                                               (31)

или для второй схемы

Α i ± 1 =Α i ± 1 ± ( - 0,5) Λ υ ⋅ V ⋅ α ⋅∆ τ ⋅∆ θ ⋅Η ¹ i ±^{- α} 1 /Ψ^* i ± ¹ 1 ^{+ α} .                                           (32)

В случае нарушения положительности коэффициентов при решении задачи в одном из направлений необходимо провести измельчение шага сетки в этом направлении, что приводит к увеличению знакоположительного компонента А и обеспечивает при определенном значении дискретных шагов устойчивость схемы.

Решение проводилось на установление переходного процесса, причем на каждом периоде колебаний проверялось выполнение условий периодичности по времени. Была проведена проверка эффективности решения задач с помощью итерационной процедуры с линеаризацией по методу Ньютона и с помощью аппроксимационной линеаризации задачи. Оценка эффективности по времени решения до выполнения условий периодичности с одинаковой точностью показывает большую эффективность использования итерационной процедуры – время решения задачи на 25...30 % меньше. Косвенная проверка эффективности проводилась также с помощью интервала значений параметра α , при которых обеспечивается сходимость численной процедуры решения без изменения шагов сетки, которая также показала большую эффективность итерационной процедуры решения задачи.

На рис. 2 представлена картина пространственного распределения давлений в слое при относительной скорости движения цилиндров V = 1,1 м/с. Функция зазора с учетом выражения для профиля поршня Ф( x ), который задан симметричным, определяется по следующему закону

Η =Η 0 - z ₀cos θ + [( Η 1 +Η 2)cos x -Η 2].                                        (33)

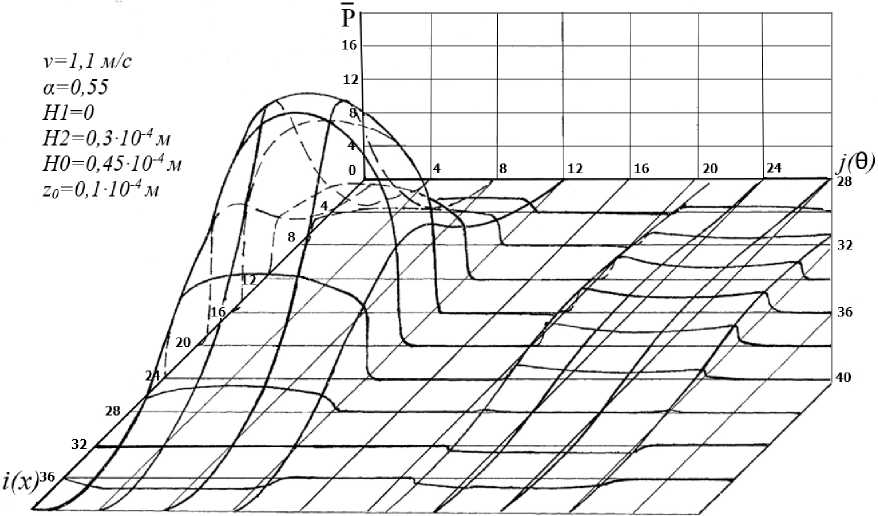
Рис. 2. Пространственное распределение давлений в слое

Как видим, наличие эксцентриситета привело к явной асимметрии распределения давлений в окружном направлении (число точек сетки в окружном и продольном направлении равны N = M = 41). Очевидно увеличение давлений для той половины слоя, для которой наблюдается минимальные зазоры, что, естественно, говорит о наличии несущей способности и жесткости слоя. Из других особенностей распределения давлений можно отметить наличие разряжений в диффузорной части зазора и некоторое смещение пика давлений в направлении движения цилиндра от симметричного положения.

Максимум давлений наблюдается в средней части хода цилиндра, т. е. там, где существует максимальная скорость движения цилиндров. Значения максимальных давлений выведены в форме графика от параметра газосодержания α и показывают рост давлений с его уменьшением

(см. рис. 3). Характерно увеличение жесткости слоя с уменьшением параметра α и ростом высоты профиля Н2. Значения жесткости слоя указаны на рисунке при α = 0,5 и также растут в представленном диапазоне изменения параметра Н2 от 15 до 170 Н/мкм.

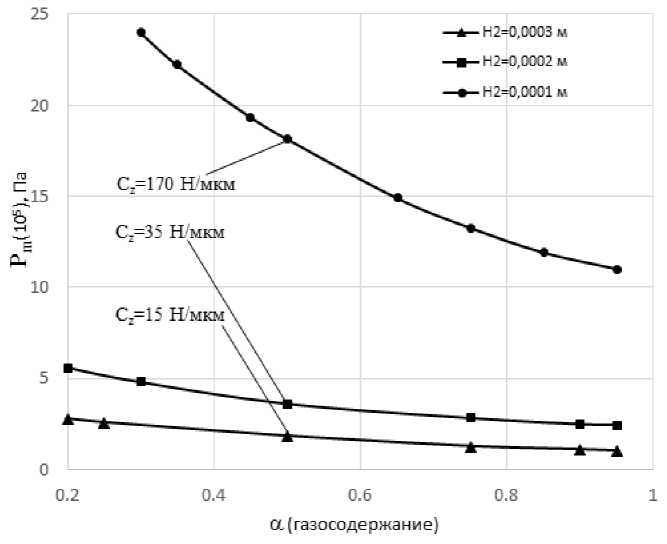
Рис. 3. Зависимость максимальных давлений в слое от параметра газосодержания

Надо сказать, что решение данной задачи может быть проведено с помощью алгоритмического и программного обеспечения задач, в которых рассмотрены бегущие волны колебаний в смазочном зазоре [15]. В этом случае функция зазора должна быть представлена в виде

Η = Η 0 - z ₀ cos θ + Η 2cos(2 πτ + x ) , (34) где длина слоя в направлении движения равна половине длины бегущей волны, так как рассматривается случай симметричного профиля. Физически это отвечает картине течения среды, когда относительное движение цилиндров остановлено, а возвратно-поступательные движения совершает профилированная часть поверхности одного из цилиндров, что и можно интерпретировать как частный случай задач с бегущей волной и частично перенести результаты исследований в работах [7, 15] на данный случай.

Выводы. Рассмотрено два способа линеаризации задачи, в первом из которых используется метод Ньютона, а второй использует идею аппроксимационной линеаризации численной схемы. Сравнительный анализ каждого из использованных подходов показывает некоторую эффективность численной схемы на основе линеаризации по методу Ньютона. Однако очевидность реализации численной схемы на основе аппроксимационной линеаризации, легкость обеспечения устойчивости численной задачи с учетом возрастающих возможностей вычислительной техники позволяют рекомендовать и этот подход.

Очевидна также необходимость «калибровки» этой модели, для устранения имеющегося в ней произвола в виде определяющей температуры и газосодержания, для расчета будущих модификаций конструкции ЦПГ выбранного типа.