К расчёту смазочной системы поршневого двигателя внутреннего сгорания

Система смазки необходима для снижения трения и износа деталей двигателей внутреннего сгорания (ДВС), отвода тепла и удаления загрязнений. Эффективность работы смазочной системы определяется правильностью её проектирования и эксплуатации [1].

Общий расход масла в двигателе определяется суммой частных расходов через подшипники, зазоры в поршневой группе и системы фильтрации [2]:

Q_общ = ∑ Q_i, где Q_i – расходы масла на отдельных участках смазочной системы.

Давление масла в системе определяется в общем виде балансом между производительностью масляного насоса и гидравлическим сопротивлением каналов [3]:

P = (Q_n / S) * R, где P – давление масла в смазочной системе, Q_n – производительность масляного насоса, S – площадь сечения всех масляных каналов системы, R – гидравлическое сопротивление масляных каналов смазочной системы. Такой подход не учитывает процессы в трибосопряжениях двигателя, смазываемых под давлением и, прежде всего, в подшипниках коленчатого вала.

Как правило, считается, что производительность насоса должна превышать потребность двигателя с учётом запаса [3]:

Q_n = K_z * Q_p, где Q_n – производительность насоса, Q_p – потребность двигателя в масле, K_z – коэффициент запаса [4]. Однако такая модель ведет к дополнительным затратам на привод насоса, холостому перекачиванию масла, снижению его функциональных свойств. В результате насос рассчитывается с учетом износа всех сопряжений на последний день работы двигателя перед ремонтом. Необходим учет каждого потребителя смазочной системы, нагрузочных и тепловых режимов двигателя.

Эффективность работы двигателя во многом зависит от функционирования его смазочной системы. Поэтому в этой области было проведено много исследований, направленных на совершенствование методов расчёта и алгоритмов моделирования смазочных систем.

До 1990-х годов методы расчёта смазочных систем двигателей внутреннего сгорания и других поршневых машин основывались, как правило, на эмпирических формулах, полученных на основе экспериментальных данных. Эти методы включали:

• -    упрощённые расчёты давления масла в каналах [3];

• -    эмпирические зависимости расхода масла через подшипники;

• -    табличные данные по потере масла на испарение и угар [5].

Основные недостатки:

• -    ограниченная точность из-за высокой степени обобщения данных;

• -    слабый учёт локальных изменений температуры и давления масла [1];

• -    невозможность анализа сложных конструкций системы смазки.

С развитием вычислительной техники в начале 2000-х годов началось активное применение численных методов расчета элементов смазочных систем:

• -    метода конечных элементов (МКЭ) для оценки несущей способности смазочного слоя в опоре скольжения;

• -    метода конечных объёмов (МКО) для расчёта гидродинамических процессов в каналах смазочной системы [6];

• -    применения вычислительной гидродинамики (CFD) для моделирования потоков смазочной жидкости в системе.

Основные достижения:

• -    повышение точности расчётов за счёт учёта реальной геометрии каналов смазочной системы;

• -    включение в расчёты тепловых эффектов и влияния вязкости масла при различных температурах;

• -    возможность анализа работы системы смазки в динамических режимах [3].

Основные ограничения:

• -    высокие вычислительные затраты [8];

• -    сложность калибровки моделей на основе реальных данных.

В 2010-х годах получили развитие комплексные подходы к моделированию, включающие:

• -    полноценные 3D-CFD-модели системы смазки [4];

• -    интеграцию термодинамических и гидродинамических расчётов [7];

• -    учёт деформации деталей [9].

Достижения:

• -    возможность анализа нестационарных режимов работы двигателя [10];

• -    учёт взаимодействия системы смазки с другими системами [11];

Методы расчёта смазочных систем ДВС за последние 30–40 лет прошли путь от простых эмпирических зависимостей до сложных многомерных моделей, использующих CFD, термодинамику и машинное обучение. Дальнейшие исследования должны быть направлены на совершенствование методов расчёта, верификацию моделей с реальными экспериментальными данными и разработку энергосберегающих решений для современных и перспективных ДВС [9].

Однако, несмотря на существенный прогресс в методах расчета смазочных систем, исследователи при этом мало внимание уделяют моделям смазки гидродинамических подшипников двигателя, хотя основными узлами трибосистемы, определяющими её надёжность, являются именно опоры скольжения жидкостного трения. Поэтому в основе метода расчета смазочной системы двигателя должен лежать гидродинамический расчёт всех опор скольжения, смазываемых под давлением. На наш взгляд, неучёт этого обстоятельства является наиболее существенным недостатком современных методов расчета смазочных систем ДВС.

В гидродинамических трибосопряжениях шип на смазочном слое в подшипнике двигается в пределах зазора по траектории, определяемой нагрузками и скоростным режимом работы машины. В поршневых ДВС это прежде всего опоры скольжения коленчатого вала, а также опоры распределительных валов, уравновешивающего механизма, турбокомпрессора. Течение смазочной жидкости через эти опоры, их гидравлическое сопротивление зависит в каждый момент времени от траектории движения шипа в подшипнике, расположения источников смазки на поверхностях шипа и подшипника, их углового положения относительно минимального зазора в сопряжении. Его нельзя считать постоянным. Кроме того, гидродинамическое давление, возникающее в опоре при работе, в десятки раз превышает давление подачи смазочной жидкости для смазки трибосопряжения. Повышение давления вызывает повышение температуры опоры и смазочной жидкости, а следовательно, падение вязкости. Смазка становится более текучей, что существенно сказывается на гидравлическом сопротивлении сопряжения [12].

Алгоритмы и методы расчета смазочных систем поршневых и роторных машин разработанные в ЮУрГУ на основе теории гидравлических цепей [13–15], учитывают эти связи и используют для расчета гидромеханических характеристик сложнонагруженных трибосопряжений уравнение Рейнольдса. Общая схема круглоцилиндрического сложногруженного подшипника показана на рисунке. Основные обозначения размеров и скоростей движения шипа и подшипника понятны из схемы. Эксцентриситет e = O1 O2 и угол 5 будут определять положение центра шипа, — = (—2 -—1) — относительную скорость его вращения, а выражения de/dt и ed5/dt - характе- ризовать относительные скорости движения центра шипа.

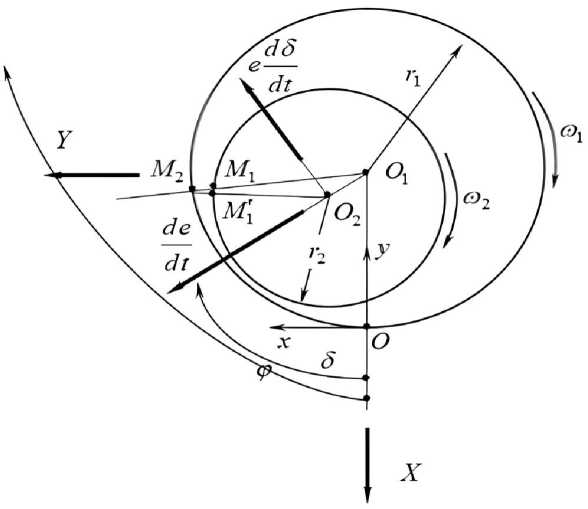
Схема сложнонагруженного подшипника Model of a complexly loaded bearing

Обозначим B - ширина подшипника, h ( ф ) = M 2 M 1 ~ M 2 М / — толщина смазочного слоя.

Используя обозначения эксцентриситета и угла линии центров, запишем толщину смазочного слоя в виде h = h0 -ecos(ф-5), где h0 - радиальный зазор, определяем ее производные по времени дh/д t = - de/dt cos (ф-5) -- ed 5/ dt sin (ф-5).

Если координаты и скорости движения шипа на смазочном слое в подшипнике известны, то поле гидродинамических     давлений p (ф, z, t) для подшипника конечной длины определяется интегрированием уравнения Рейнольдса [12]:

д

h 3 р д p ^Л

дф( 12 ц Э дф J

д

+-- д z

h р ^д p — ( 12 ц _Э д z )

— — (h р) + — hh р) .

2 дф      дт

В формуле h = h/h₀;     ^р=р/р о ; й э =р э /ро ; p = p v ² /ро ® о > v= h o/ r ; z = zr ,

- a <  z <  a , a = B/D ;        ф = x/r ;          ю = ( ® ₂ -Ш 1 )/o ₀ ; т = ш ₀ 1 .

В этих выражениях использованы известные обозначения, приведенные в монографии [12].

Значения безразмерных толщины смазочного слоя и ее производной определяются из выражений h = 1 -%cos(ф-5),  дh/дт = -^хcos(ф-5) + /5sin(ф-5)] , где относительный эксцентриситет шипа обозначен х = e/ho ; производные положения шипа по безразмерному времени обозначены х, б.

Уравнение Рейнольдса для конечного подшипника интегрируют в области □ = ( фе 0,2 п ; z g- a , a ) , при этом, как правило, используют граничные условия Свифта -Штибера:

p (^ф , z =± a ) = p_a ; p ( ^ф , z ) = p ( ^ф + 2 n z ); p (^ф , z ) > ⁰ , p ( ф , z ) = p_s  на ( ф , z ) gQ _s , S = 1,2... S *.

В этих условиях используется понятие источников смазки на поверхности шипа и подшипника в виде канавок и отверстий. Количество этих источников обозначено S . Область источника смазки Q s , характеризуется допущением, что давление постоянно и равно давлению подачи смазочной жидкости в данный момент времени p_s .

Граничные условия Свифта - Штибера работают таким образом: когда в какой-либо точке области интегрирования Q в процессе расчета гидродинамических давлений по уравнению (1) не выполняется условие p >  0, давление в этой точке приравнивается к нулю.

Использование граничных условий (2) позволяет хорошо описать физику процесса разрыва смазочного слоя в районе максимальных гидродинамических давлений. Однако эти условия некорректно представляют границу начала эпюры давления. Такое обстоятельство не позволяет точно определить баланс расходов смазочной жидкости, поступающей и вытекающей из опоры. Торцевой расход жидкости может оказаться значительно больше, чем расход из источника на входе в опору. В результате в процессе компьютерного моделирования смазочной системы при отсутствии давления подачи смазочной жидкости на входе в подшипник масляное голодание не наступает и расчет продолжается. Кроме того, допущение о полном заполнении смазочной жидкостью зазора между шипом и подшипником при выводе уравнения Рейнольдса не позволяет корректно использовать его для моделирования смазочных систем.

Для того чтобы преодолеть это недостаток граничных условий (2), предлагается использовать граничные условия Якобсона - Флоберга - Ольсена, позволяющие выполнить условия неразрывности смазочного слоя в гидродинамической опоре скольжения:

p ( ф , z = ± a ) = 0; p ( ф , z ) = p ( ф + 2 п , z );

^p ( ^ф р , z ) =^d p / ^{дф ( ф} р , z ) = ⁰; ^{p ( ф} в , z ) = ⁰; (3)

p ( ф , z ) = p_s на ( ф , z ) gQ _s , S = 1,2... S *.

Здесь ф _р , ф в - границы разрыва и восстановления смазочного слоя.

В этом случае граница восстановления смазочного слоя становится физически более обоснованной. Реализация условий Якобсона - Флоберга - Ольсена базируется на идее Элрода и Адамса [16-18] по расчету гидродинамических давлений в смазочном слое на основе интегрирования универсального уравнения (4) для степени заполнения зазора 0 :

д Г h ^Зр   ,_мде1 д Г h ³Р   ,_мде1 ю д        д _А

—     g ( 6 )— +— ^ g ( 6 )— =т- ( h 0 ) + -( h 0 ) .                     ⁽⁴⁾

дф 12 ц Э      дф    o z 12 ц Э      o z    2 дф       дт '

Здесь Р = Ру ² /ц _о ю _о - безразмерный коэффициент сжимаемости смазки, р- его размерное значение, g ( 6 ) - переключающая функция:

,      Г1, если 0 >  1;

g      [ 0, если 0 <  1.

Степени заполнения 6 приписывается двоякий смысл. В области давлений 6 = р/р c , где р c -плотность смазки при давлении, равном давлению кавитации p_c . В области кавитации p = p_c , р = р _c , причем 6 определяет массовое содержание жидкой фазы (масла) в единице объема пространства между шипом и подшипником.

Гидродинамические давления связаны с 6 соотношением p = pc + g (6)₽ln 6.  (5)

Оригинальные методы решения универсального уравнения (4), разработанные в ЮУрГУ, приведены в работах [19, 20]. Результаты решения являются физически обоснованными, что позволяет использовать эти алгоритмы для моделирования смазочных систем ДВС, с учетом динамики и смазки гидродинамических опор скольжения коленчатого вала и других трибосопряжений, смазываемых под давлением, прогнозировать режимы масляного голодания опор.

С практической точки зрения такой подход позволит проектировать опоры скольжения и смазочные системы ДВС на новом уровне, снизить потери мощности на привод масляных насосов, не применять насосы с избыточной производительностью.