К распространению звуковых волн в двухкомпонентной наследственно-упругой среде

Вопросам динамики двухкомпонентных сред посвящены работы [1-7], в которых рассматриваются упругие волны в однородной, насыщенной жидкостью неограниченной пористой среде. В [8, 9] решаются вопросы диссипативных процессов при гармоническом деформировании наследственно-упругой среды.

Для одномерного случая систему уравнений движения двухкомпонентной наследственно-упругой среды запишем в виде [1, 2]:

Раскрывая определитель, будем иметь:

⁽ Y 11 Y 22 ⁺ Y 122 ^{— ( 4 ) + (} Y 11 ^а 22 ⁺ Y 22 J ^— — 2 у ₁₂ а ₁₂) G *^{2 )} — ² ( a + i p ) ^{( 2 )} +

[ Ц

+1 — а ₂2

( H ²²

—

а 2 1 G ⁴ ( a + i p ) ⁴ = 0, в = ^{— 12} J                                П

ц и ⁽ X ) + A 1 и , ⁽ 2 ) = P 11 u ^:1 ■ P 12 u ^{( 2 )}            (1)

A 1 и , ⁽ XX + A 2 и , ⁽ XX = P ₁₂ u '⁽¹⁾ + P ₂₂ u '⁽²⁾

Выразим упругий оператор ц через ядро релаксации – дробно-экспоненциальную функцию Ю.Н. Работнова, имеющую в пространстве Фурье вид [11]:

Здесь ц - модуль сдвига; А 1 , А 2 - коэффициенты, зависящие от пористости среды и модуля сжимаемости жидкости; р ₁₂ -коэффициент динамической связи скелета и жидкости [1] ( р ₁₂ >0); P ii = P 1 / а 1 и P 22 = P 2 / а 2 — истинные плотности наследственно-упругой компоненты и жид-

ц = ц » ^—

А ц

^{1 + ( —т} ц ^{) Y} ,

где т „ ц ц», ц

- время релаксации; А ц = ц » - ц ₀,

– нерелаксированное и релаксирован-

ное значения модуля; у

–

структурно-

кости в порах; P 1 , P 2 - массы компонент в единице объема среды; a 1 , a 2 – величины, характеризующие доли объема смеси, занимаемые каждой компонентой ( a 1 + a 2 =1, a 1 >0, a 2 >0).

Индексы, стоящие вверху в круглых скобках относятся соответственно: 1 – к наследственно-упругой компоненте, 2 – к жидкости. Точка над буквой означает производную по времени, а индекс внизу, стоящий после запятой, указывает дифференцирование по координате x .

Систему (1) перепишем в виде:

чувствительный параметр (параметр дробности), 0 <  у <  1. При у =1 наследственные свойства сдвиговой деформации описываются моделью стандартного линейного тела.

Преобразуем (6) к виду:

^{Ц (1)} M⁽²⁾- М⁽¹⁾+У 1720 _п ^u , XX ^{+ а} 12 ^u , XX = ^2 V 11 u ^{+ Y} 12 u ⁾ HG

^ 2 ^{M +}< ^ 22 ^M (^ =     ( V г^^{1 +} V 2 U ^(2> )

12 , xx 22 , xx        2    12           22

G

Ац sin ПУ ц = g + i -—2 hh g = / Цо у + Ц»(—ТЦ У +(Цо + "»)cos ^^ (—тц /                           2

h = ( ¹ у +^{( —т} ц У + ^2cos ^7 ^{( —т} ц У               ²

Подставим (7) в (5), получим:

^{( у} 11 Y 22 ^{+ у} 12 ^{— +}

A 1         A 2

^ 12     yr , ^а 22         ,

HH

Y 11 =       / 12 = ^P . Y 22 = ^P

^у 11 ^а 22 ⁺ h Y 22   ^{2 у} 12 ^а 12 | ⁺

P

P

P

2 H

^H = ^ц + 2 A ⁺ A 2 , ^P = ^P 11 ^{+ 2 P} 12 ^{+ P} 22 , ^G = -- ^P

Решение системы (2) ищем в виде:

^{( 1 —} цо/A jsin ^^

⁺ i Y 22 M »-------;-----—

h

G² — ² ( a + i p ) ² +

и(5*= N(5* exp(i—t — Qx) 6 = a + i —, 5 = 1,2, (3) c где а - коэффициент затухания волн; го - круговая частота; с – скорость волны.

Подставим (3) в (2), после преобразований, получим:

+

^{а 22} gy h

g 1 = ^M »

—

^an | ^{+ i a} 22 ^M »

^{( 1 —} цо/ц „⁾

h

G ⁴ ( a + i p ) ⁴ = 0

^оЩ у + ( —т , 1 +I 1 + So- 1 cos SL ,M

^{( —т} ц 7           l ц »у     ²

= ц„

» H

| у— » ² + Ц G ²6 ² j C ^{( 1 )} + ( Y 12 — ² + а_п G ²6 ² C ^{( 2 )} = 0 (4) ( у ₁₂ — ² + а ₁₂ G ² 6 ² C ^{( 1 )} + ( у ₂₂ — ² + а ₂₂ G ² 6 ² C ^{( 2 )} = 0, где ц - упругий оператор.

Для того чтобы однородная система имела нетривиальное решение, ее определитель, составленный из коэффициентов при C ^{( 5} ) ( 5 = 1,2 ) , должен быть равен нулю.

Из (8) получим квадратное уравнение относительно z:

к — ⁴ z ² + ( a 1 + ia ₂ ) G ² — ² z + ( d 1 + id ₂ ) G ⁴ = 0 (9)

2                      g 1

k = ^у 11 ^у 22    ^Y 12 , a 1 = ^Y 11 ^а 22 ⁺ , ^Y 22    2 ^Y 12 ^а 12

h

a 2 = у 22 h ^{— 1} M »

1 — ц^ I sin Пу, d 1 = а 22 g 1 h1 — ai2, l   ц-J 2

d 2 = а 22 h -1 M »[1 — ц° I sin ^у, l   ц»)    2

где z – компл ексное число.

ВестникВГУИТ, №1, 2014

Оно находится по формуле:

z = ( a + i β )^{- 2}, β = ω c

Решение уравнения (9) запишем в виде:

G ²

z =-       ( b ₁ + ib ₂ )

2 k ω ²

b ₁

ϕ cos 1 , b

2,2

ϕ sin 1 , r

2,1

= δ 1 ² + δ 2 ²

δ ₁ = a ₁ ²

-

a 2 ²

-4kd1,δ2 = 2(a1a2 -2kd2), δπ tgϕ1 = 2 ,0 ≤ϕ1 ≤

δ 1           2

Из (11) с учетом (10) определим характеристики звуковых волн в насыщенной жидкостью наследственно-упругой пористой среде: квадрат скорости распространения волн:

c ₁ ² ₂ =      ^{r 2 G}      sec ² ϕ ²

^,     2 ( γ ₁₁ γ ₂₂ - γ ₁ ² ₂ ) 2

^ϕ sin ¹

^ϕ cos ¹

r ₂ = b ₁ ² + b ₂ ² , tg ϕ ₂ =

11 ₂ коэффициент поглощения [12]:

ωϕ a = tg 2 c2

логарифмический декремент затухания:

δ = 2 π tg ϕ ₂ ²

По формулам (12) и (13) построены графики зависимости скорости и коэффициента затухания от температуры и частоты при следующих данных: σ 11 =0.85, σ 22 =0.25, σ 12 =0.05, γ 11 =0.95, γ 22 =0.05, γ 12 =0, М ∞ =2, µ o / µ ∞ =0.1, ω =1 или τ =1.

Значения параметра дробности γ указаны на рисунках.

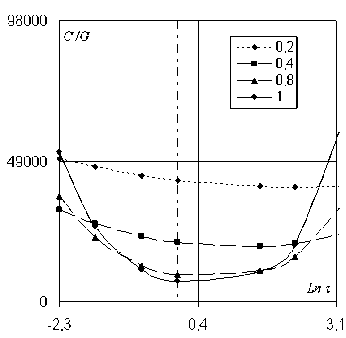
Рисунок 1. Зависимость скорости от температуры

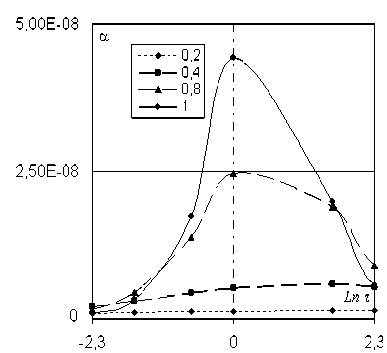
Рисунок 2. Зависимость коэффициента затухания от температуры

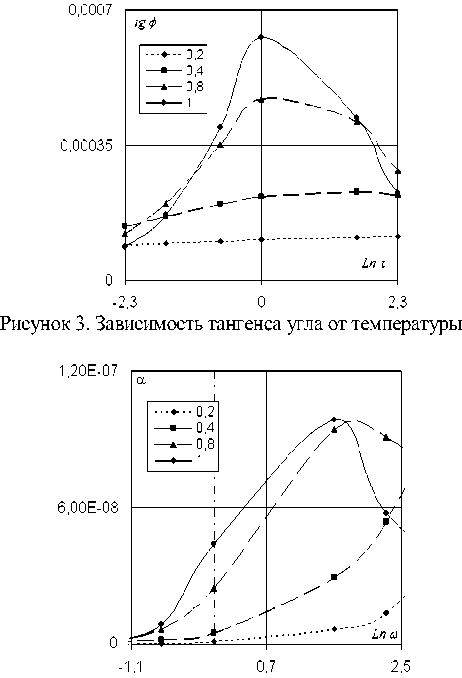
Рисунок 4. Зависимость коэффициента затухания от частоты

Рисунки 1-3 представляют зависимости скорости, коэффициента затухания и тангенса угла сдвига фаз от логарифма температуры, рисунок 4 – зависимость коэффициента затухания от логарифма частоты. Зависимости скорости и тангенса угла сдвига фаз от частоты идентичны зависимостям от логарифма температуры.