К разработке теории структурной политики роста: основания на макро- и микроуровне
Автор: Сухарев Олег Сергеевич
Журнал: Вестник Пермского университета. Серия: Экономика @economics-psu
Рубрика: Экономическая теория
Статья в выпуске: 1 т.15, 2020 года.
Бесплатный доступ
Целью настоящего теоретического исследования является разработка основных положений теории структурной политики, которые могут быть применимы в рамках решения проблем экономического роста. Актуальность структурной политики во многих странах существенно возросла, особенно в период развернувшихся рецессионных явлений, замедления темпов роста. Однако на теоретическом уровне анализа вопросы связи структурной политики с другими видами политики, а также экономической динамикой, определяемой темпом роста валового внутреннего продукта, другими процессами в экономике - распределением инвестиций, технологическим обновлением - исследованы недостаточно, особенно с точки зрения связи макро- и микроуровня, происходящих экономических изменений. Предметом исследования является получение строгих аналитических соотношений, связывающих на макроэкономическом уровне экономический рост и структуру инвестиций и технологий, а также выделяющих режимы структурных изменений на микроэкономическом уровне в рамках структуры «заработная плата / прибыль». Методологию исследования составляют современные теории экономического роста неоклассического и эволюционного (шумпетеровского) направлений науки, которые не учитывают влияние структурных элементов экономики на её динамику, а также общий эконометрический подход проектирования экономических моделей. Применение указанных теоретических разработок с выявленными в них недостатками позволило получить новый результат - структурную модель оценки вклада инвестиций в новые и старые технологии в темп экономического роста, выделить режимы изменения технологичности экономики, состоящей из двух базовых секторов, при взаимном влиянии друг на друга. Новым результатом можно также считать полученное условие технологического обновления и переключения режимов «созидательного разрушения» и «комбинаторного наращения» в зависимости от соотношения скоростей отвлечения ресурсов от старых производств и создания ресурсов под новые производства. Кроме того, сформулирована теорема о соотношении затрат, определяющая в виде условия оптимальное соотношение производственных и трансакционных издержек в рамках любой экономической системы, где эти виды издержек можно выделить. Выделены режимы изменения структуры «заработная плата / прибыль», позволяющие установить единственный режим доминирования труда по динамике заработной платы, а также получена структурная формула, позволяющая выделить вклад элементов цены в ее повышение. Разработанные в ходе исследования положения позволяют, с одной стороны, обеспечить формирование общего контура теории структурной политики, с другой - составляют перспективу развития методов структурного анализа и могут быть применены для обоснования структурных изменений в экономике. В перспективе это позволит управлять переключением режимов технологического развития на макро- и микроуровне.
Экономическая структура, сектор, старые и новые технологии, инвестиции, заработная плата, прибыль, структурная политика, экономический рост
Короткий адрес: https://sciup.org/147246805
IDR: 147246805 | УДК: 330.341.4 | DOI: 10.17072/1994-9960-2020-1-5-24
Текст научной статьи К разработке теории структурной политики роста: основания на макро- и микроуровне
Э кономическая наука признаёт структурные изменения довольно сложным явлением.
При этом авторитетные экономисты, такие как Й. Шумпетер и Д. Норт [1; 2], считали, что именно посредством изменения структуры происходят фундаментальные изменения в экономике, и они связаны с экономической динамикой – ростом [3–5]. Правда, если согласно шумпетеровскому подходу [6–9], пропорции меняются под действием силы появления новых комбинаций (новаций различных видов), то Дуглас Норт отмечал [1], что ценовые пропорции являются генератором институциональных изменений, что приводит к организационным трансформациям и смене экономических пропорций (структур). Конечно, цена является понуждающим институтом, так как калькулируется по жестким правилам. Более того, структура цены отражает уже сложившиеся соотношения в экономике, по крайней мере в производстве того продукта, цена на который рассматривается [6]. Цена уникальна тем, что содержит компоненту, отражающую организацию производства внутри фирмы, и компоненту (прибыль), которая показывает влияние рынка, т. е. действий иных агентов, их эффективность и способность принимать те или иные решения в рамках рыночной конкуренции. Вместе с тем цена содержит налоговую компоненту, что является отражением участия правительства в формировании этого института, причём данная компонента диктуется ещё жестче, чем другие, которые можно изменить в текущем режиме, например получив экономию каких-то затрат, найдя дешёвый труд, либо проявив активность в продажах и получив дополнительную прибыль. Поэтому соотношение цен является как причиной, так и следствием изменения пропорций, структуры экономики, выражением происходящих изменений.
Структурные изменения бывают разными - постепенными, охватывающими длительный период времени, либо довольно скоростными, принимающими вид структурных сдвигов, иногда очень значительных по масштабу. Хотя масштабные изменения структуры всё-таки требуют длительного периода, но в современной экономике это правило уже не является незыблемым постулатом, так как возросли скорости изменений, увеличился их пространственный масштаб (в силу процессов глобализации). Структурные изменения происходят и на коротких интервалах времени [10; 11]. Это обстоятельство выдвигает требование к обоснованию структурной политики, которая уже ориентируется не только на длительный, но и на относительно короткий период. При этом одной из её задач выступает определённый темп экономического роста [5; 12].
Структурная политика относится к одному из самых сложных видов политики. Причина не только в том, что трудно предсказать, как будет функционировать новая структура, а также каковы затраты на изменение сложившейся структуры, но и в том, что имеющаяся структура может сопротивляться воздействиям по её изменению, обладать инерцией динамики и при недостаточной обоснованности и аналитической неточности предлагаемых мер не измениться [13]. В таком случае происходит обесценивание мероприятий структурной политики, они оказываются нейтральными по отношению к сложившейся структуре. Причина данной нейтральности может быть не в том, что меры не сработали, а в том, что стандартные мероприятия макроэкономической политики нейтрализовали структурную политику.
Иными словами, структурная политика, которую подают как особый тип воздействий на экономику, причём обычно долгосрочно ориентированных, оказывается зависимой от текущих мер макроэкономической политики, влияющих на структурную динамику. Кроме того, институциональные коррекции, ставшие чуть ли не основополагающим методом современной политики правительств, обладают весомым воздействием на структурную динамику. Как видим, существенным является вопрос о разделении не только целей проводимой политики, но и инструментов. Например, меры по противодействию безработице и росту занятости обязательно повлияют на рынок труда [12], и, что важно, - на его структуру, причём на различные аспекты этой структуры (возрастную, профессиональную, по видам деятельности, по доходам и т. д.). Совокупность этих «структурных моментов» создаст общий сдвиг в функционировании рынков труда, но он может охватить далеко не все отрасли или виды деятельности, так как политика в области труда может быть дифференцированной и касаться определённых видов экономической деятельности в большей степени, нежели иных.
Чтобы разработать правительственные меры, влияющие на экономическую структуру, причём как на долю элемента в системе (статика), так и на его темп (динамика), требуется применять аналитические подходы для выяснения того, как именно связаны элементы в системе, в чём состоят движущие силы их динамики, связь структурных изменений и роста [14–17]. Вопрос технологической структуры и распределения инвестиций между различными видами технологий становится с этой точки зрения центральным, так как именно использование имеющегося ресурса позволяет освоить созданные новые технологии и вывести экономику на новые параметры производительности [14; 16]. Рассмотрим два уровня структурной политики. Во-первых, макроэкономический, который реализуется посредством простой модели «старые/новые» технологии и инвестиции в них. Во-вторых, микроэкономический уровень в виде моде- ли двух секторов с изменяющимися затратами, структуры «заработная плата / прибыль», определяющей режим функциони- рования экономических структур.
Макроструктурный подход: техно- логии и инвестиции
Именно технологическая динамика определяет облик современных экономик- лидеров. Однако связь структурной динамики, технологических изменений и эко- номического роста изучена весьма скромно [5; 6; 14]. В частности, неоклассические модели роста [3; 10], а также модели структурных сдвигов [16; 17] позволяют определить в лучшем случае вклад некоторых факторов в рост. Однако они не позволяют получить вариантов развития (сценариев), особенно в аспекте влияния технологий или оценки связи риска, заданного институциональными характеристиками системы (перманентно изменяющимися), и перемещения ресурсов между секторами (внутри экономики). Иными словами, внутренние структурные изменения остаются как бы безучастными к развитию, хотя составляют это развитие по содержанию. Пропорции становятся правилами, влияющими на перемещения ресурсов, обеспечивая возможности технологической модернизации. Эволюционные модели в отличие от неоклассических исследуют аспекты реструктуризации экономики, например в рамках неошумпетерианского направления за счёт появления новых комбинаций [6].
Важно то, что секторальное развитие в основополагающей степени определяется состоянием располагаемых ресурсов. Если присутствуют ограничения по ресурсам, то развитие экономики только за счёт неких коррекций институтов или создания стимулов будет явно ограничено. Ресурсы на развитие рассматриваемых секторов могут быть получены не только извне либо из резервов, но и от тех секторов, развитие которых можно признать избыточным как раз по обеспечению ресурсами. Данный ресурс может быть отвлечён и использован на развитие от иных видов деятельности - это и составляет центральное звено современной структурной поли- тики, особенно в эпоху динамичных изменений. Например, одни секторы высокорентабельны и низкорискованны, другие, наоборот, низкорентабельны и высокорискованны. Исправление такой «структурной вилки» представляет одну из задач теории структурной политики.
В экономике присутствуют как минимум два больших типа технологий - новые (недавно созданные, передовые) и уже используемые (применяемые) технологии. Инвестиции в рамках такой дихотомии также распределяются по данным двум типам технологий. Если имеются два сектора (обрабатывающий и трансакционно -сырьевой), то в рамках каждого из них имеется дихотомия «новые/старые» технологии. То есть продукт в секторах экономики можно представить производимым на новых (n) и старых (s) технологиях. Тогда можно записать, что продукт каждого сектора представляет собой сумму продуктов, произведенных на новых и старых технологиях в этом секторе: Y1=Y1n+Y1s , Y2=Y2n+Y2s . Технологичность секторов, определяемая как отношение объёма производства на новых технологиях к объёму производства на старых технологиях для каждого сектора примет вид y1=Y1n/Y1s , y2=Y2n/Y2s (Y1n , Y2n - производство в каждом секторе на новых технологиях Y1s , Y2s - производство на старых технологиях). Структурный коэффициент экономики K=Y1/Y2=d1/d2 примет следующий вид: K=(Y1n+Y1s)/(Y2n+Y2s) , где d1 , d2 - доля каждого сектора в общей величине создаваемого продукта.
Запишем структуру производства на старых технологиях по секторам в виде коэффициента P=Y1s/Y2s . Тогда K=fi(1+y1)/(1+y2) . Также учтём, что структурный параметр экономики X=(1--K)d2=[1 +у2—в(1 +y1)]d2/(1 +у2) .
Найдём производную dK/dt и запишем условие для структурных изменений dX/dt<0 , dX/dt>0 .
Имеем:
dK1
= к [ dt dX1
= d 2[ s — K ( + p + s)], dt p dt
1 d / 1 1 d v 2
где p =-------—
1 + / 1 dt 1 + y 2 dt
.
Откуда получаем условие структур- ных изменений с учётом технологической структуры. Если условие без учёта этой структуры можно считать общим условием структурных изменений (реструктуризации экономики), то с учётом технологической структуры его можно обозначить как специальное условие. Получаем:
dX
< dt
0,
ЭЛ 1 d e
2) + и + s > 0, в dt
K >
s
1 d e в dt
+ и + s
dX
> dt
0,
1 d e n
+ и + s > 0, в dt
K <
s
1 d e в dt
+ p + s
Как показано выше, X=[1+y2--- —0(1+y1)]d2/(1+y2) . Продифференцировав данное выражение dX/dt , рассмотрим условие dX/dt>0 , т. е. рост доминирования второго сектора. Взяв производную и положив результат больше нуля, можно расписать условие, когда достигается этот результат, а именно (приняв g p =(1/0)d0/dt ):
s (1 + y 2 - в(1 + /1)) > 0, дв < -и-
Откуда имеем два варианта:
-
1) s > 0,
у 1< у 2 / в + (1- в )/ в , (3)
g ^ < - и ;
-
2) s < 0,
У 1 > у 2 / в +(1- в )/ в , (4)
д в < - и -
Темп роста структуры производства на старых технологиях ( g p ) должен быть меньше взвешенных изменений технологичности в первом и втором секторах. Это является одним из условий роста экономики, состоящей из двух секторов.
Возможны ещё два варианта, обеспечивающие dX/dt>0 :
-
3) s < 0,
Y 1< у 2 / в + (1- в )/ в , (5)
-
д в > -и ;
-
4) s > 0,
У 1 > у 2 / в +(1- в )/ в , (6)
g p > - и -
Аналогично можно получить варианты для ситуации, когда усиливается доминирование первого сектора и dX/dt<0 (Эти варианты не приводятся, так как получить их не представляет больших трудностей.)
В ситуации доминирования второго сектора X>0 (при 0=1/2 ; 1; 2 ) получим графическое решение у1<(1-0)/0+у2/0 (см. рис. 1).
Условие выполняется соответ ственно для различных 0 по линиям, ограничивающим технологичность у 1 сверху, -FF, OO, EE. Тем самым при данной технологичности у2 * для каждой величины 0 технологичность у 1 будет ниже величины, задаваемой указанной линией, той точкой, где данная линия пересекает перпендикуляр от точки γ2* (рис. 1).
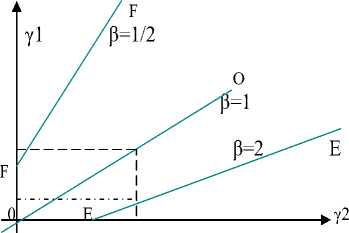
Рис. 1. Графическое представление условия по технологичности первого сектора при доминировании второго сектора ( γ1>0 , γ2>0 )
Fig. 1. Diagram of the technological efficiency in the first sector, when the second sector dominates (γ1 > 0, γ2 > 0)
Далее запишем условие экономического роста, выраженное через темп роста первого и второго секторов, и получим ограничение на темп роста второго сектора при условии, что экономика растёт, какой бы ни был темп роста первого сектора.
Используем исходные выражения, приведённые выше: K=Y1/Y2, X=(1–K)d2 . Кроме того, было получено, что dK/dt=K(g1–g2) , то есть g K =g1–g2 – темп изменения структурного коэффициента. Структурная формула позволяет записать: g=g1d1+g2d2 . Экономический рост – g>0 .
Имеем g=gKd1+g2>0. Приняв во внимание, что gK=gβ+μ, получим g = (gp + V)d 1 + g2 > 0.
Откуда g2 > (b2gr2 - b1 gri - gp)d 1, b1 =
-Y L; b 2 = -^-, 1 + y 1 1 + y 2
технологичности за вычетом взвешенного темпа изменения структуры старых технологий двух секторов (взвешивающие коэффициенты соответственно b2d1 , b1d1 , d1 ). Темп роста первого сектора должен превосходить темп роста второго сектора, взвешенный на обратный структурный коэффициент со знаком «минус».
Инвестиции распределяются между секторами, но в границах секторов инвестируются новые и старые производства, новые и старые технологии. В общем смысле риск инвестирования новых и старых технологий должен отличаться, однако зачастую недостаточно статистических данных, чтобы так разделить риск. Для структурной динамики важно то, каким образом соотносится темп изменения создаваемого дохода и темп роста риска. Это в существенной степени детерминирует выбор инвестиционных решений, что и сказывается на результате распределения инвестиций между уже существующими и вновь появляющимися возможностями. Иногда появление нового невозможно без инвестиций, агенты идут на значительный риск ради раскрытия эффекта новизны, чтобы затем в течение довольно длительного времени использовать этот эффект для получения прибыли и иных дивидендов.
Представим инвестиции в общем виде I=Is+In как сумму инвестиций в старые (Is) и новые (In) технологии. Пусть связь инвестиций и технологичности (γ) такова, что бóльшему уровню технологичности (хотя бы для его поддержания) нужна бóльшая величина инвестиций как в старые, так и в новые технологии. В связи с этим можно записать Is=a+bγ, In=c+dγ. Инвестиции в новые технологии обеспечиваются за счёт некоторой доли (α) инвестиций, которые отвлекаются от инвестиций в старые технологии, плюс некая величина вновь созданного ресурса, который инвестируется в новые технологии (μ). Можно полагать, что α и μ независимы. Конечно, возможен вариант развития, когда доля отвлекаемого ресурса от старых технологий и доля вновь создаваемого ресурса каким-то образом связаны. Отсюда запишем In=aIs+,In или In=aIs/(1-,)=nIs, где n=a/(1-,).
Теперь несложно выразить
I=(a+bY)(1+n) , Y=(na—c)/(d—nb) .
Найдём изменение (dY/dt) (темп роста gY=(1/y)dy/dt) технологичности в зависимости от параметров инвестиционной функции и структуры распределения ресурсов, задаваемой отвлечением и созда- нием инвестируемого ресурса. Тогда na - c
Г = , d - nb
_ d n ad - cb g ? dt ( n a — c )( d — n b )
Инвестиции можно записать так:
I=(a+bY)(1+n), продукт Y=I/o, где о - норма инвестирования. Тогда g=gI-go>0 - для экономического роста системы.
Введя Va=da/dt, V,=d,/dt соответственно скорости отвлечения и создания инвестируемого ресурса (отвечают прин- ципу «созидательного разрушения» и «комбинаторного наращения» [18]), взяв производную по времени - dn/dt, подста- вив в gI, получим d + b gl = [Va + nV, ],
( d - n b )(1 - , + a )
(d + b)[Va + nV, ] „ g = - ga > 0.
( d - n b )(1 - , + a )
Откуда имеется ограничение (формула (10)) на рост нормы инвестирования, чтобы был обеспечен экономический рост:
( d + b)[V a + n V , ] -----------— > g
(d - n b )(1 - , + a ) '
Если норма инвестирования изме- няется несущественно на каком-то интервале времени, то go=0 и тогда темп роста будет
= ( d + b )[ V a + n V , ]
g ( d - n b )(1 - , + a )
Обозначим
Q = ( d + b )
( d - n b )(1 - , + a )
Тогда g = Q\Va + nV,] > 0. (11)
Теперь можно выделить два условия (выражение (12)) экономического ро- ста, определяемого структурой распределения инвестиций в старые и новые технологии с соответствующими скоростями отвлечения и создания инвестиционного ресурса:
-
1) ^>0 , V a >-nV , ; (12)
-
2) ^<0 , V a^ -nV , .
В первом случае, чтобы наблюдался экономический рост, необходимо превышение скорости отвлечения инвестиционного ресурса от старых технологий над взвешенной скоростью создания ресурса под новые технологии. Правая часть неравенства 1 в выражении (12) взята со знаком «минус», который обозначает разно-направленность процесса отвлечения и создания ресурса. Взвешивающий коэффициент представляет соотношение долей отвлечения и создания ресурса [ η=α/(1–μ) ].
Во втором случае для экономического роста требуется, чтобы скорость отвлечения ресурса была меньше взвешенной скорости создания ресурса со знаком «минус».
Например, ситуация, когда Ω>0 , то ( d + b )
есть ----------------- > 0 , достигается
( d - n b )(1 - , + a )
при b>0 и a0 (заведомо), η>0 (заведомо). Теоретически возможен вариант для ^>0 при b>0 и dd(1-,)/b . Аналогично рассматриваются условия для Ω<0 , распространяемые на параметры d , b , a , ,.
Прилагая представленный алгоритм структурного анализ к каждому сектору отдельно, получим условия роста и структурных изменений. Эти условия выражены через общую величину инвестиций в секторы и в старые технологии в каждом секторе. Именно инвестиции в старые технологии определяют возможности изменений технологической структуры, а также говорят о сложившемся режиме технологического развития (насколько сильна зависимость от существующей технологической базы и какова склонность к её изменению).
Связь инвестиций в новые и старые технологии в первом и втором секторах представлена следующими соотношениями:
1 - P 1 + a 1 In1 =----------- Is1 = ц 1 Is1,
1 - ^ 1
-
1 - ^ 2 + a 2
In 2 = — ------ Is 2 = n 2 Is 2,
-
1 — ^ 2
I1=In1+Is1; I2=Is2+In2 , I=I1+I2 ,
Y=I/o , Y=Y1+Y2 , K=Y1/Y2 , Y=(1+K)Y2 , (13) g=gI-ga>0 , g=g1 d1+g2 d2 , d1=Y1/Y , d2=Y2/Y , X=d2-d1=(1-K)d2 , gK=g1-g2 , 1=П1 Is1+n2 Is2 , gI=h1 u1+h2 u2 , где h1=I1/I , h2=I2/I, u1=gn1+gIs1 , u2=gn2+gIs2 .
Условие роста экономики g>0 , откуда go
Если второй сектор растёт g2>0, возникает ограничение на темп структурного коэффициента K:
роста
h 1 u 1 + h 2 u 2 — g ^
g K <
d 1
.
Изменение структуры задаётся dX/dt<0 , dX/dt>0 .
Тем самым имеем
X=(1-K)d2, dX/dt=-d2(dK/dt)+(1-K)dd2/dt.
Полагая dXdt <0, получаем K>s/(g1––
-g2+s) при g1>g2-s , где s=(1/d2)dd2/dt .
Если
dX/dt>0
, то
K при g1>g2-s.
Располагая выражениями для темпа роста экономики, несложно получить темп роста каждого сектора, установленный через темп роста инвестиций, который, в свою очередь, выражен через темп соотношения долей отвлечения и создания ресурса и темп роста инвестиций в старые технологии в данном секторе. Тогда получим:
g1=h1 u1+h2 u2-ga+gK d2, g2=h1 u1+h2 u2-go-gKd1, (14) При g>0, g1>gK d2, g2>-gK d1.
Если располагать достоверной зависимостью продукта в секторе от инвестиций, то несложно с учётом полученных соотношений исследовать влияние на условие роста и структурных изменений распределения инвестиций в новые и старые технологии.
Совмещённое условие роста и изменений структуры можно оформить следующим образом.
Запишем продукт как Y=(1+K)Y2. Найдём производную dY/dt, подставив K=Y1/Y2, получим g=d2dK/dt+g2, dX/dt=g2-g+s(d2-d1). (15)
Условие структурных изменений и роста
-
1) dX/dt<0 , g>0 ;
-
2) dX/dt>0 , g>0 .
Для двух случаев имеем g2>(d1-d2)s , чтобы экономика росла при происходящих структурных изменениях. Если нужны какие-то определённые изменения структуры, например, в пользу первого сектора, то dX/dt<0 и все выкладки, проведенные ранее, должны быть применены для этого случая.
Экономический рост можно представить по структурной формуле g=g1 d2+g2 d2>0, откуда g2>-g1 d1/d2.
Следовательно, g1>d2(d2-d1)s/d1 , рост первого сектора должен превышать величину справа, чтобы экономика росла и изменялась её структура. Для управления структурными изменениями необходима целевая функция формирования экономической структуры, которую вводят в приводимые здесь выкладки.
Динамика секторов зависит от их технологичности и потребляемых ресурсов. Однако, если представлять экономику в виде некой системы секторов, взаимодействующих друг с другом, детерминация выглядит сложнее, поскольку существуют институциональные ограничения динамики, задающие цели изменения структуры либо ограничивающие структурное изменение в какую-либо сторону, - dX/dt>0 либо dX/dt<0 . Возможен вариант структурной статики, когда экономическая структура длительно не изменяется dX/dt=0 . В таком случае релевантными являются выкладки, касающиеся обеспечения темпа роста.
Инвестиции в новые и старые технологии детерминируют динамику рассматриваемых двух секторов. В связи с этим можно записать, что I=I1+I2, I1/Y=i1, I2/Y=i2 - величина инвестиций каждого сектора в общем продукте экономики. В каждом секторе наблюдается процесс конкуренции старых и новых технологий и инвестиций в них. Причём он имеет свои характеристики, так как существует специфика производства в секторах. Поэтому, вводя долю отвлечения и создания ресурса в каждом секторе соответственно α1, α2, μ1, μ2, можем записать, учитывая, что сумма инвестиций в новые и старые технологии в каждом секторе равна величине инвестиций этого сектора, I1=I1s+I1n, I2=I2s+I2n. На основе того, что I1n=α1 I1s/(1–μ1),
I2n=α2 I2s/(1–μ2) , получим
1 1 = [1 + 1 - ] 1 1 n , a l
1 2 = [1 + 1 — ^ 2 ] 1 2 n.
a 2 (16)
Инвестиции в секторах выражены через инвестиции в новые технологии в этих секторах, где параметры α1, α2, μ1, μ2 соответственно доли отвлечения ресурса от существующих технологий и создания нового ресурса под новые технологии в первом и втором секторах.
Пусть Vα1=dα1/dt , Vμ1=dμ1/dt , Vα2=dα2/dt , Vμ2=dμ2/dt . Тогда найдём dI1/dt и dI2/dt , получим темп роста инвестиций в секторы, выраженный через темп роста инвестиций в новые технологии в секторах и соотношение скоростей и долей отвлечения ресурса от существующих технологий и создания под новые технологии.
Тогда gl 1 = gl 1 n
—
a1VM1 + (1 — ^1)V„1 a12 + (1 — ^1)a1’
= _ a 2 V , 2 + (1 — ^ 2) V a 2
g1 2 g1 2 n a 22 + (1 — ^ 2) a 2 ’
Обозначим для простоты записи a1V^ + (1 — ^1)Va1 мм1 о’ a12 + (1 — ^1)a1
a 2 V, 2 + (1 — ^2)Va 2 ^2.
a 22 + (1 — ^ 2) a 2
Отсюда gl 1 = gl 1 n — Q1’ gI 2 = gI 2 n —“2.(18)
Далее преобразуем приводимую ранее структурную формулу для темпа экономического роста (исходя из Y=C+I+G+NX=C+I1+I2+G+NX) . Дифференцируя по времени и преобразуя, получаем g = gcC + i1 g i 1 + i 2 g i 2 + g G a + g Nx b .
Подставляя значение для темпа роста инвестиций в секторах, выраженное через темп инвестиций в новые технологии, получим оценку вклада развития новых технологий (v1n, v2n) в темп экономического роста. Это и представляет собой результат оценки структурной динамики через структуру инвестиций.
Запишем структурную формулу в следующем виде:
g = gs +i1( g i 1 n — Q 1 )+ i 2( g i 2 n — Q 2 )+
+gGa+gNXb, v1 n = i1 gi 1 n ’ v2n = i2gi2n . (19)
Если рассмотреть экономику в целом, обозначив is=Is/Y, ω=In/Is, I=In+Is, то инвестиции представляют собой сумму инвестиций в новые и старые технологии, и несложно, используя структурный подход, показать вклад инвестиций в новые и старые технологии в темп роста экономики. Учтём, что di T dm
= is + (1 + m)’ dt dtdt dm
= m [ g in — g is ] . dt
Получим g=gc c+is ω gIn+is gIs+ +gG a+gNX b .
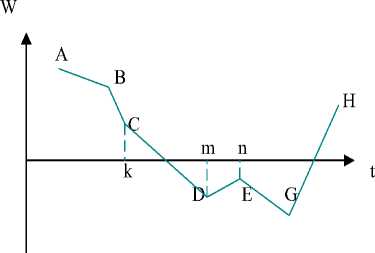
Если ω<1, то есть In Вклад в общий темп роста экономики инвестиций в новые технологии будет больше вклада в темп роста инвестиций в старые при условии, что темп роста инвестиций в новые технологии будет превосходить темп роста инвестиций в старые, взвешенный на величину, обратную отношению величин инвестиций в новые и старые технологии. А именно: gIn>gIs/ω. Тем самым получено точное условие по оценке вклада инвестиций в темп роста, которое можно применить, располагая статистикой по инвестициям в новые и старые технологии. Также можно сравнить вклад в темп роста в два сектора экономики в рамках двухсекторной модели. Подводя некоторый итог, отметим, что вклад инвестиций в новые технологии в каждом секторе в общий темп роста экономики определяется произведением доли инвестиций этого сектора в продукте на величину темпа роста инвестиций в новые технологии. Если темп роста инвестиций в новые технологии положительный, а, скажем, величина Q1>0 и ^2>0, то вклад всех инвестиций в сектор i1gI1+i2gI2 будет меньше на величину i1Q1+i2Q2, чем вклад инвестиций в новые технологии. Это вызвано эффектом распределения инвестиций между старыми и новыми технологиями, соотношением скоростей и долей отвлечения и создания инвестиционных ресурсов. Доли отвлечения и создания инве- стиционных ресурсов под новые технологии, скорости изменения этих долей явля- ются институциональными характеристи- ками экономики и существенно влияют на вклад данных типов инвестиций в темп экономического роста. В свою очередь, соотношение долей, отражающих наличие эффекта «созидательного разрушения» и «комбинаторного наращения», может рас- сматриваться как характеристика экономической структуры и как соотношение скоростей. Иными словами, можно ввести два структурных параметра si=a/^ и s2=Va/V^. Взяв производную параметра si по времени dsi/dt, найдем ds1 = 1 V - α V . dt µ α µ2 Подставив Va=s2V^, получим ds11 = Vµ[s2 - s1]. dt При условии структурной статики dsi/dt=0, откуда si = Va/V^, то есть si=s2, отношение долей отвлечения и создания ресурса равно отношению скоростей изменения этих долей. Однако это неполное условие структурной статики, поскольку μ≠0, и если доля создаваемого ресурса под новые технологии постоянна на рассматриваемом интервале времени, то V^=0, что отвечает dsi/dt=0. Для структурной динамики dsi/dt<0 или dsi/dt>0 (конечно, динамика может сопровождаться и изменением скоростей и их отношений, что представляется отдельным случаем для рассмотрения). При dsi/dt>0 имеем два варианта: 1) Vp>0, s2>si: соотношение скоростей превышает соотношение долей отвлечения и создания инвестиционных ресурсов, причём скорость создания ресурса под новые технологии - положительная; 2) V^<0, s2 При dsi/dt<0 имеем также два варианта: 1) V^>0, s2 При эволюции технологий и экономики происходит переход из одного режима структурной динамики в другой, что связано как с характеристиками технологий и их взаимодействием, так и с изменяемыми институтами, определяющими процесс технологического обновления. Перемещение ресурсов между секторами символизирует ситуацию следующим образом: для сектора, из которого ресурсы вытекают, это отвлечение, для сектора, в который они притекают, это поступление для него нового ресурса. Именно эти два процесса диктуются текущей технологической структурой и действующими правилами, определяющими разницу в доходности (прибыльности) секторов и рисках ведения хозяйственной деятельности. Причём эта разница выступает относительно перемещения ресурсов и распределения инвестиций самостоятельным правилом. Стимулирование экономического роста за счёт решения подобных структурных проблем видится на основе изменения соотношения по инвестициям в старые и новые технологии, что предполагает разветвлённую систему мер в целях технологического обновления и повышения производительности труда. В ряде авторских исследований было показано, что перемещение капитала между секторами можно оценивать согласно модели, где перемещение ресурсов определяется в зависимости от отношения инвестиций в старые технологии к валовой добавленной стои- мости, отношения рисков в секторах и рентабельностей, динамике труда между секторами [19–21]. Уровень технологичности1 может быть принят как некая функция, представляющая отношение инвестиций в новые и старые технологии, которые в секторах зависят от риска. Здесь можно применять показательные функции, связывающие инвестиции и риск Такого рода модели и продемонстрированный здесь подход могут применяться в рамках подготовки сценарных прогнозов и мер структурной политики. Более того, использование представленного подхода в рамках теории структурной политики крайне необходимо с точки зрения формирования стратегии экономического развития, ориентированной как на длительный, так и относительно короткий период. При этом необходимо учитывать влияние микроэкономических аспектов изменения экономической структуры. Микроэкономическое содержание структурной политики: затраты, прибыль и их влияние на изменение экономики Структура затрат, с одной стороны, может быть характеристикой экономического развития, с другой – является результатом сложившихся хозяйственных пропорций. Проблемы динамики затрат в экономической науке изучены весьма непло- хо, однако имеется соотношение между производственными и трансакционными затратами, которое является показательным при анализе функционирования различных экономик. Под производственными, или трансформационными, затратами понимаются все затраты, связанные с про- изводством продуктов, под трансакционными – затраты заключения сделок, поиска информации, каналов сбыта, рекламы, об- служивания, оказания услуг, т. е. непроизводственные затраты. Для отдельных секторов, например услуг, трансакционные затраты выступают в качестве общих затрат. Для производства характерны и производственные (трансформационные), и трансакционные затраты, поскольку имеется целая инфраструктура, обслуживающая производство продуктов. В связи с этим, если рассматривается производственный сектор, то полные издержки включают и трансакционную часть издержек. Если рассматривается сектор услуг, то для него полные издержки – это трансакционные издержки, тем самым они также на уровне бухгалтерии учитываются. В связи со сказанным противопоставление данных двух типов затрат видится как некорректное. С точки зрения проведения экономических исследований, в которых применяется структурный анализ затрат, необходимо ориентироваться на показатель соотношения трансакционных и производственных (трансформационных) издержек KI=Tr/M, где Tr – трансакционные, M – трансформационные (производственные) затраты. Это актуально для экономики, где присутствуют два вида издержек, как и два сектора – обрабатывающий и трансакционный. Чем ниже трансакционные издержки на единицу производственных (трансформационных) издержек, тем эффективнее развивается данная экономика. Действительно, в экономике необходимая эффективность будет достигаться при условии, что коэффициент отношения затрат стремится к минимуму, когда производственные издержки не растут. Иными словами, минимизация коэффициента KI осуществляется не за счёт роста производственных издержек dM/dt≤0. Для поиска экстремума положим dKI/dt=0 при соответствующих изменениях функции KI, удовлетворяющих условию минимума. В точке экстремума темп роста трансакционных издержек равен темпу роста производственных издержек. Снижение коэффициента К будет обеспечено dK/dt<0 при gTr Запишем ситуацию с прибылью в каждом из двух рассматриваемых секторов (r1, r2), составляющих экономику. Предста- вим r1=Y1(N1)–M(Y1, N1)–Tr(Y1, N1), (22) r2=Y2(N2)–m(Y2, N2)–tr(Y2, N2), где Y1, Y2 – доход (продукт) каждого сектора, M, Tr – производственные и трансакционные издержки первого сектора, m, tr – про- изводственные и трансакционные издержки второго сектора, зависящие от величины до- хода и занятого в секторе персонала. В экономике создаётся продукт: Y=Y1+Y2. Пусть K=Y1/Y2=d1/d2, d1=Y1/Y, d2=Y2/Y, d1+d2=1, пусть M=aTr, m=btr – производственные издержки составляют некую долю от трансакционных. Величина, обратная эффективности секторов: z1=(M+Tr)/Y1=(1+a)Tr/Y1, z2=(m+tr)/Y2= =(1+b)tr/Y2. Откуда r1=Y1(N1)–(1+a)Tr(Y1, N1), (23) r2=Y2(N2)–(1+b)tr(Y2, N2). Структурные параметры для эконо- мики из двух секторов примут вид r 1 + (1 + a )Tr K =-----------, r 2 + (1 + b) tr X = (1 - K) d 2. Если коэффициенты структуры затрат не изменяются a=M/Tr, b=m/tr и экстремум прибыли достигается при dr1/dt=0, dr2/dt=0, тогда dY1/dTr=1+a, dY2/dtr=1+b. При изменяющихся коэффициентах затрат условие роста прибыли dr1/dt>0, dr2/dt>0, увеличения дохода dY1/dt>0, dY2/dt>0, получим dY 1 dt da dTr > Tr + (1 + a)----, dt dt Окончательно имеем, введя q1= =M/Zq2=m/z, доли материальных затрат в общих затратах сектора q1 gTr < л . gM, 1 + q1 q 2 gtr < gm. 1 + q 2 Темп роста трансакционных издержек в секторах должен быть ниже взвешен- ного темпа роста производственных затрат в этих же секторах, чтобы росла прибыль и создаваемый в секторах продукт. Запишем Y=Y1+Y2=r1+(1+a)Tr+r2+ +(1+b)tr, продифференцировав по времени dY/dt и положив больше нуля, как условие роста экономики, получим (структура затрат не изменяется, прибыль экономики равна сумме прибыли двух секторов): dY dr1 Z1 . dTr dr 2 . +---+ (1 + a)----+----+ dt dt dt dt dtr +(1 + b) > 0, dt a,b – const, p = r1 + r 2. Тогда для экономического роста необходимо, чтобы изменение прибыли превышало сумму взвешенных темпов роста трансакционных издержек в секторах (весовые коэффициенты k1, k2 представляют собой суммарные затраты в каждом секторе, то есть k1=M+Tr, k2=m+tr), взятую со знаком «минус». Закономерно снижение издержек и отрицательный темп роста обеспечивают необходимость положительного темпа роста прибыли. Положительная динамика (темп роста трансакционных затрат) делает также необходимым условием превышение темпа роста прибы- dY 2 db ddtr -----> tr + (1 + b) . dtdt dt Откуда, учитывая, что ли, но в таком случае этот темп может должны расти, запишем da 1 + a >gTr, db >gtr. 1 + b (25) секторы быть отрицательным (и даже равен нулю). Запишем данное условие: dp >- (k1gTr+k2gtr ). dt Конечно, динамика издержек в секторах отличается: в одном может наблюдаться снижение издержек (отрицательный темп), в другом – повышение (положительный темп), поэтому сумма взвешен- ных темпов может давать отрицательную или положительную величину (E), так что dp/dt>E (при E<0), и dp/dt>–E (при E>0). Графически ситуация представлена на Рис. 2. Графическое изображение условия роста по dp/dt Fig. 2. Diagram of dp/dt growth Зона роста экономики, исходя из рис. 2, простирается вправо от линии IOI для данного значения величины E, когда оно выше или ниже нуля. Ситуация существенно усложняется, если структура затрат перманентно изменяется: в условии роста появляется темп роста структуры затрат, взвешенных на величину материальных затрат в секторе, а именно dp > - (Mga + mgb + k 1 gTr + k2gtr )’(30) dt Записав прибыль секторов через их эффективность r1=(1–z1)Y1 и r2=(1–z2)Y2, положив условие роста прибыли gr1>0, gr2>0 и роста продукта секторов g1>0, g2>0, получим g1=gr1+(1–z1)dz1/dt, g2=gr2+(1–z2)dz2/dt, откуда g1>(1–z1)dz1/dt, g1>0, g2>(1–z2)dz2/dt, g2>0. (31) Поскольку, как было показано выше, gK=g1–g2 и согласно структурной формуле g=g1d1+g2d2, d1+d2=1, то g=gKd1+g2>0 или gK>–g2/d1. При росте первого сектора g1>0 структурный коэффициент, чтобы экономика росла, должен превысить отношение темпов (второго к первому сектору) со знаком «минус»: K>–g2/g1, g1>0. В точке экстремума прибыли gr1=0, gr2=0, откуда имеем 1 - z1 dz 2 K >---. 1 - z2 dz1 (32) Таким образом, структурный коэффициент должен превзойти взвешенное изменение эффективности второго сектора по эффективности первого сектора (формально величины z1, z2 – обратные эффективности, чем они выше, тем ниже эффективность, чем ниже – тем выше экономическая эффективность). Используя Y=Y1+Y2 и K=Y1/Y2, получим Y1=KY/(1+K), Y2=Y/(1+K), тогда величины z1, z2 можно выразить так: z1=(1+a)Tr/Y1=(1+a)(1+K)Tr/(KY), z2=(1+b)tr/Y2=(1+b)(1+K)tr/Y. Далее представим условие, когда второй сектор менее эффективен, нежели первый z2>z1, и наоборот, когда второй более эффективен, чем первый z2 В первом случае Tr/tr<(1+b)K/(1+a), отношение трансакционных издержек секторов должно быть меньше правой части. Во втором случае получается обратное неравенство Tr/tr>(1+b)K/(1+a). Тем самым трансакционные из- держки первого сектора меньше взвешен- ной величины трансакционных издержке второго сектора, когда второй сектор экономически менее эффективен, и больше, когда второй сектор более эффективен, нежели первый. Представив прибыль в каждом секторе r1=(1–z1)Y1 и r2=(1–z2)Y2, исследуем функцию прибыли на экстремум dr1/dt=0, dr2/dt=0 и получим dr 1 dt — — Y1 + — (1 — z1) = 0, dt dt dr2 =- dzl y 2 + dH (1 — z 2) = 0. dt dt dt (33) Откуда можно записать dY1/Y1=dz1/(1–z1), dY2/Y2=dz2/(1–z2). Интегрируя эти выражения, получим Y1(1–z1)= exp(c1), Y2(1–z2)=exp(c2), где c1, c2 – константы интегрирования, c=c1–c2. Подставляя Y1=KY2 и деля первое на второе, получим K(1–z1)/(1–z2)=exp(c), (34) r1/r2=K(1–z1)/(1– z2). Поэтому оптимальная прибыль первого сектора равна оптимальной прибыли второго, помноженной на экспоненту в степени константы интегрирования: r1*=r2*exp(c) (оптимальную прибыль обозначили r1*, r2* соответственно для первого и второго секторов). Учитывая r1>0, r2>0, принимая вариант, что второй сектор доминирует по доле в продукте экономики, то есть X=d2– –d1>0, получим условие изменения струк- туры при таких исходных параметрах: X = r 2(1 - z1) - r 1(1 - z 2) a > о, r 2(1 - zl) d 2 > 0. (35) Анализируя полученное выражение (35) для X, несложно прийти к следующему заключению: при доминировании второго сектора по доле в продукте r2/r1>(1–z2)/(1–z1), что равносильно K<1, при доминировании первого сектора по доле в продукте r2/r1<(1–z2)/(1–z1), что равносильно K>1. Учитывая проделанные выкладки, сформулируем теорему соотношения затрат, описывающую условие минимизации трансакционных издержек на единицу материальных затрат в каждом секторе. Дадим общую формулировку. Предварительно введём следующие обозначения. Пусть эффективность в секторе Z1=Y1/(M+Tr), Z2=Y2/(m+tr). Целевые коэффициенты K1=Tr/M, K2=tr/m стремятся к минимуму, при условии dM≤dTr, dm≤dtr. Величина выработки каждого сектора y1=Y1/N1, y2=Y2/N2, где N1, N2 – численность занятого персонала в секторе. Удельные издержки в каждом секторе на одного занятого: i11=M/N1, i12=Tr/N1, i21=m/N2, i22=tr/N2. Теорема соотношения затрат. Оптимальная структура затрат (при dM≤dTr, dm≤dtr, т. е. достигаемая не за счёт роста материальной компоненты издержек) достигается при условии, когда темп роста выработки равен сумме темпов роста эф- фективности и трансакционных затрат на одного занятого. Доказательство. Запишем для секторов: y1=Z1(M+Tr)/N1=Z1(i11+i12); y2=Z2(i21+i22), K1=i12/i11=[y1/(Z1i12)–1]-1; K2=[y2/(Z2i22)–1]-1. Возьмём производные по времени К1 и К2, то есть dK1/dt=0, dK2/dt=0. Получим темпы роста соответствующих обозначенных выше величин: gy1=gZ1+gi12, gy2=gZ2+gi22. Тем самым показано, что темп роста выработки равен сумме темпов роста эффективности и удельных трансакционных издержек на одного занятого. Обязательным условием выступает dK1/dt<0 и dK2/dt<0 при t Находя W1=gy1–gZ1–gi12 и W2=gy2– –gZ2–gi22 и определяя, насколько эта величина отличается от нуля, можно говорить о том, как далека ситуация от оптимальной структуры затрат. На рис. 3 отражена графическая методика определения отклонения от оптимального соотношения затрат. Рис. 3. Динамика параметра W, характеризующего близость к оптимальному результату величиной отклонения от нуля Fig. 3. Trend for the W parameter which is closer to the optimal result by zero line divergence На рис. 3 показан вариант дискретного изменения параметра W по точкам A, B, C, D, E, G, H. Наиболее близкие значения к оси абсцисс (времени) в точках k, m, n, причём самое близкое расстояние – nE. Именно для этой точки ситуация наиболее близка к оптимуму. Однако выбор зависит от того, как изменяется производная структурного параметра K, так как исследователя может интересовать как минимум, так и максимум (а не оптимум вообще). Например, в одном случае ситуация может быть близка к режиму сырьевого, а в другом случае – несырьевого развития. По параметру W можно это установить с учётом изменения знака dK/dt в окрестности рассматриваемой оптимальной точки. Эта методика нашла апробацию в ряде предыдущих работ, а здесь представлена в общем виде, вытекающем из сформулированной теоремы затрат [22–26]. Конечно, эффективность сектора предусматривает оценку всех видов издержек, поэтому сформулированная теорема не отвечает строгим признакам теоремы, скорее всего, это аналитически полученное условие, которое можно использовать при оценке структуры затрат. Однако и теорема Коуза в подлинном смысле не отвечает «званию теоремы». Представленную теоретическую композицию полезно использовать при структурном анализе развития секторов и экономических систем, оценке структурных сдвигов. Полученные соотношения представляют, если угодно, динамическую версию эффективности функционирования экономической системы, в данном случае – рассматриваемых секторов. Соотношение «заработная плата / прибыль» выступает ещё одним релевантным структурным параметром при исследовании эффектов структурной политики на микроэкономическом уровне. Важно учитывать взнос динамики прибыли, заработной платы и иных материальных затрат в общий рост цен – инфляцию, выстраивая макроэкономическую политику борьбы с инфляцией соразмерно взносу в её темп этих частей цены и дохода. Если представить структуру цены P=w+m+f+n, где w – заработная плата, m – материальные затраты, f – прибыль, n – налоги, то структурная формула изменения цены будет выглядеть так: gp = d 1 gw + d2gm + d3gf + d4gn , (36) где d1=w/p, d2=m/p, d3=f/p, d4=n/p – доли заработной платы, материальных затрат, прибыли и налогов в цене, gp, gw, gm, gf, gn – темп роста цены заработной платы, материальных затрат, прибыли и налогов. Как видим, чем выше доля налогов в цене, тем при прочих равных будет выше темп роста цены при положительном росте налогов. Если ввести рентабельность r=f/(w+m), несложно получить P = (1/r +1) f + n, gp = d3 gf(1/r + 1) - d3 gr / r + d 4 gn • (37) Из выражения (37) видно, что чем выше темп роста рентабельности, тем ни- же темп роста цены, чем выше падение рентабельности, тем выше темп роста цены. Тем самым понижение эффективности способствует росту цены, т. е. рост цены может означать понижение экономической эффективности. Чем выше сама рентабельность, тем при прочих равных ниже темп роста цены. Введём обозначения: общие затраты Z=w+m, цена P=w+m+f (налоги не принимаем во внимание), величина прибыли – f. Кроме того, примем такие важные соотношения: K=w/m – структура затрат, показывающая долю заработной платы в затратах; норма прибыли u=f/Z (или доля прибыли в затратах); h=w/f – структура «заработная плата / прибыль». Это важ- нейший структурный параметр, показывающий соотношение заработной платы и прибыли в экономике или доминирование труда или капитала, которое можно обозначить по увеличению заработной платы (gh>0, то есть gw>gf), когда темп роста заработной платы превосходит темп роста прибыли (это условно можно обозначить как доминирование труда), или по увеличению прибыли (gh<0, то есть gw Темп роста цены определяется тем- пом роста нормы прибыли, заработной платы и материальных затрат, а именно: g = _U_g + Sm+Kg. sp 1 + u^u 1 + K • Увеличение нормы прибыли составляет интерес владельца капитала, поэтому gu>0. Располагая gK=gw-gm, gu=gf-gz, gZ=gw-gK/(1+K), получим условие для темпа роста прибыли, чтобы норма прибыли увеличивалась: gf > gw gK 1 + K ■ У наёмного работника, не владею- щего капиталом, интерес сводится к увеличению заработной платы, то есть gw>0, заработная плата растет. Если её темп обгоняет темп роста прибыли, то структурный коэффициент h будет возрастать gh>0, в обратном случае - понижаться gh<0. При этом в исходной точке данный параметр может быть больше или меньше единицы – важна динамика, изменение структуры, которое и показывает, как меняется содер- жание экономических событий, какая группа агентов доминирует, стремясь к реализации своего интереса. Рассмотрим всех устраивающий случай, когда растут и заработная плата, и прибыль (gw>0, gf>0), важно лишь, как изменяется соотношение заработной платы к прибыли, т. е. величина h(t)=w/f. Владельца средств производства интересует норма прибыли, символизирующая отдачу, т. е. прибыль на единицу затрат (включая инвестированный капитал), а именно gu>0, откуда gf>gZ, gf>gw-gK/(1+K). Поскольку в правую часть неравенства, определяющего условие роста нормы прибыли, входит структурный параметр K и темп его роста gK, постольку именно знак этого темпа определит дальнейшие соотношения, как представлено в таблице. Оценка динамики структуры затрат Trends in costs structure Структура затрат – K (gK), K>0 (заведомо) Структура «заработная плата / прибыль» – h(gh) Результат динамики с учётом условия роста нормы прибыли (gu>0) Оценка соотношения темпа роста заработной платы и прибыли gK>0, gw>gm Величина заработной платы в затратах увеличивается gh>0, gw>gf Заработная плата растёт быстрее прибыли, соотношение h увеличивается (доминирует труд) gf>gw-gK/(1+K), gf Доминирует труд, заработная плата растёт быстрее прибыли (норма прибыли тоже растёт) gh<0, gw Заработная плата растёт медленнее прибыли, соотношение h уменьшается (доминирует капитал) gf>gw-gK/(1+K), gf>gw, имеем gf>gw Доминирует капитал, при быль растёт быстрее gK<0, gw Величина заработной платы в затратах уменьшается gh>0, gw>gf Заработная плата растёт быстрее прибыли, соотношение h увеличивается (доминирует труд) gf>gw +gK/(1+K), так как gK<0, gf Темп роста прибыли больше большей величины и меньше меньшей (пустое решение) gh<0, gw Заработная плата растёт медленнее прибыли, соотношение h уменьшается (доминирует капитал) gf>gw +gK/(1+K), так как gK<0, gf>gw, имеем gf>gw+gK/(1+K) Доминирует капитал, прибыль растёт быстрее заработной платы Из таблицы следует, что единственная ситуация, когда доминирует труд, складывается при условии, что растёт величина заработной платы в затратах, при этом темп роста заработной платы обгоняет темп роста прибыли. Конечно, собственник производства может пойти на такое решение, зависящее целиком от него, только в том случае, если исходная величина заработной платы крайне низка, т. е. h много меньше единицы. Во всех иных случаях доминирует тот, от кого зависят решения в части найма персонала, калькуляции затрат, управления производством – собственник (владелец средств производства) и т. д. Таким образом, мотивы структурных изменений и технологического обновления заложены на микроэкономическом уровне не только соотношением заработ- ной платы и прибыли, но и базисными ин- ститутами, определяющими темп измене- ния этих релевантных параметров. Заключение В ходе проведенного теоретического исследования проблем обоснования структурной политики получены условия, совмещающие такое изменение экономической структуры, которое сопровождается экономическим ростом. Во-первых, определён вклад инвестиций в новые и старые технологии в темп экономического роста. Это позволяет развернуть дальнейшие меры воздействия в сфере стимулирования технологического обновления и управляемых изменений технологической структуры. Во-вторых, обозначено соотношение в рамках исследования структуры затрат, позволяющее применить графиче- скую методику оценки отклонения от оптимального уровня. Чем выше это отклонение, тем выше ограничения на изменение соотношения производственных и трансакционных издержек в рамках проводимой структурной политики на микроэкономическом уровне. Кроме того, выделены режимы динамики структуры «заработная плата / прибыль» на микроэкономическом уровне структурных изменений, позволяющие определить тип доминирования капитала или труда, что не может не повлиять на дальнейшие экономические изменения. Таким образом, разработан полезный исходный теоретический аппарат, позволяющий на уровне простейших моделей и соотношений по элементам охарактеризовать экономическую динамику, что в дальнейшем позволит дифференцировать методы экономической политики.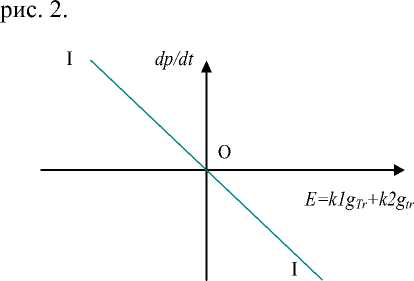
Список литературы К разработке теории структурной политики роста: основания на макро- и микроуровне
- Норт Д. Институты, институциональные изменения и функционирование экономики. Пер. с англ. А.Н. Нестеренко; предисл. и науч. ред. Б.З. Мильнера. М.: Фонд экономической книги "Начала", 1997. 108 с.
- Шумпетер Й. Теория экономического развития. Капитализм, социализм и демократия. М.: Эксмо, 2007. 864 с.
- Aghion P., Akcigit U., Howitt P. Lessons from Schumpeterian Growth Theory // American Economic Review. 2015. № 105 (5). P. 94-99.
- Aghion P., Ufuk A., Howitt P. The Schumpeterian Growth Paradigm // Annual Review of Economics. 2015. № 7. P. 557-575.
- Gabardo F.A., Pereima J.B., Einloft P. The incorporation of structural change into growth theory: A historical appraisal // EconomiA. 2017. № 18 (3). P. 392-410. DOI: 10.1016/j.econ.2017.05.003


