К решению задачи количественного регулирования в системах теплоснабжения

Постановка задачи. Как это хорошо известно, в системах централизованного теплоснабжения в РФ преимущественно используется качественное регулирование процесса [1, 2]. Вместе с тем по данным работы [3] в Дании, Германии, Финляндии и Швеции «…системы теплоснабжения…работают на принципах количественного регулирования». Указывается, что в сетях этих стран температура теплоносителя либо стабилизируется на уровне в 110 °С, либо ступенчато изменяется в диапазоне 100+120 °С. Аналогичные сведения о количественном регулировании процесса теплоснабжения содержатся и в работе [4]. В этой же работе также отмечается, что относительно низкие температуры теплоносителя положительно влияют на работу теплоэлектроцентралей (ТЭЦ) и способствуют снижению потерь теплоты при ее транспортировке. Также в работе [4] подчеркивается, что при такой концепции построения систем теплоснабжения – когда температура прямой воды является const и не зависит от погодных условий – все регулирование процесса сосредоточено в тепловых пунктах самих потребителей. Это, во-первых, дает возможность им самим регулировать процесс в зависимости от их собственных нужд, а во-вторых, способствует и энергосбережению. Конечно, при этом температура и расход теплоносителя в подающих магистралях самой тепловой сети должны позволять решать задачи регулирования на тепловых пунктах потребителей должным образом, т. е. теплообменное оборудование потребителя должно быть способно «снять» с теплоносителя нужное по погоде количество теплоты. Только при таком условии в здании будет поддерживаться требуемая температура внутреннего воздуха.

К месту заметим, что проблема количественного регулирования в РФ стала актуальной в основном из-за вынужденного (по разным причинам) снижения температуры теплоносителя в подающих магистралях тепловых сетей, которое началось примерно с 90-х годов прошлого столетия. При этом теплоснабжающими организациями заявляется, что потребное количество теплоты, якобы, доставляется «расходом», однако при этом обычно не разъясняется, как и каким образом конкретно решается эта задача.

Зарубежный опыт построения систем региональной энергетики обсуждается в работе [5].

В работе [6] проведен сравнительный анализ энергетической эффективности работы ТЭЦ при количественном и качественном способах регулирования тепловой нагрузки. Отмечено, что при количественном регулировании тепловой нагрузки, во-первых, повышается энергетическая эффективность ТЭЦ за счет увеличения теплофикационной выработки электроэнергии турбинами на 9,5 %, во-вторых, расход топлива водогрейными котлами уменьшается на 9 % (объясняется это меньшим количеством одновременно работающих котлов и снижением продолжительности их работы в отопительный период), и в-третьих, снижается расход электроэнергии на транспорт теплоносителя в два раза.

О снижении расхода электроэнергии на перекачку теплоносителя при количественном регулировании сообщается и работе [1, с. 119–120].

Таким образом, как это следует из вышеизложенного, переход на количественный метод регулирования систем теплоснабжения в общем обещает быть достаточно эффективным, однако при этом есть некоторые проблемы с конкретными алгоритмами регулирования, с тем, когда и каким образом следует изменять расход теплоносителя на теплоснабжение [7, 8]. Поэтому необходима проработка указанных вопросов. О такой необходимости говорится, в частности, и в работе [7], в которой указаны проблемы, которые необходимо решать при применении количественного регулирования в условиях, когда в эксплуатируемых тепловых сетях волевым методом предполагается заметное снижение температуры прямой воды. При этом, в частности, отмечается, что существенное увеличение расхода теплоносителя неизбежно приведет к неудовлетворительной работе элеваторных узлов.

О необходимости проработки задачи регулирования указано в работе [8], в данной работе предложен свой подход к построению алгоритмов регулирования, при этом учитываются теплофизические свойства греющей и нагреваемой воды в теплообменниках, термические сопротивления стенок каналов или трубок и слоя накипи и прочие характеристики.

Предлагаемое решение задачи. Как это отмечено выше, при управлении теплоснабжением за счет изменения расхода все регулирование процесса должно быть сосредоточено в тепловых пунктах самих потребителей, поэтому есть смысл найти алгоритм управления именно для такого случая. Такой подход вполне целесообразен еще и из-за того, что погодное регулирование на централизованном источнике теплоты в принципе для каждого конкретного здания является достаточно грубым, не обеспечивающим поддержание температуры внутреннего воздуха на заданном уровне с удовлетворительной точностью. Как это отмечено в работе [9, с. 458], централизованное регулирование «… ориентировано на обезличенное здание в районе действия тепловой станции при расчетной температуре внутреннего воздуха 18 °С (расчетная температура согласно СНиП в наиболее представительном помещении в рядовой жилой комнате жилого дома)». Однако так называемый погодный график должен быть индивидуальным для каждого конкретного здания с его вполне конкретными теплозащитными свойствами и вполне конкретной системой отопления. Данный график можно построить, если приравнять мощность системы отопления к теплопотерям здания.

Согласно работам [10–12] мощность системы отопления W СО можно вычислить по следующей формуле:

W co = (kF) co (t co - t b )/[1 + (kF) co /(2cG co )], (1) где c и G_СО – удельная теплоемкость и массовый расход теплоносителя через систему отопления соответственно, t_СО и t_В – соответственно температура воды на входе системы отопления и температура внутреннего воздуха, (kF) _СО – это тот параметр, который подлежит определению при идентификации модели системы отопления [13]. В данном случае, как это обычно принято в литературе, система отопления здания представляется эквивалентным отопительным прибором.

Теплопотери здания, как это хорошо известно, определяют по формуле Н.С. Ермолаева [1, 9]:

Q = q v ■ (t B — t n ) ■ V, (2)

где qV – удельная тепловая характеристика здания, V – его объем, tН – температура наружного воздуха.

Приравнивая соотношения (1) и (2) и разрешая полученное равенство относительно GСО , получим, что

G eo =

_____q y Vtj B— t n lllkF co_____

^2c[^(kF) co ^(t co ^- 1 в ) ^- q y ^y(t B ^- I h^)]

. (3)

Вполне понятно, что в данную формулу вместо tВ подставлена tЗВ – заданная температура внутреннего воздуха.

Данный алгоритм следует использовать в системе автоматического управления (САУ) отоплением: имея оценку теплозащитных свойств здания в виде его удельной тепловой характеристики qV , а также решив задачу идентификации для его системы отопления – определив параметр (kF) СО , по фактической температуре наружного воздуха и заданной температуре внутреннего воздуха вычисляется необходимый расход воды на его систему отопления.

Анализ и корректировка полученного решения. На рис. 1 для здания с q_y = 0,86 Вт/(м-°С), (kF)_co = 4300Вт/°С, V = 8000 м ³ приведены графики изменения расхода G_СО в зависимости от

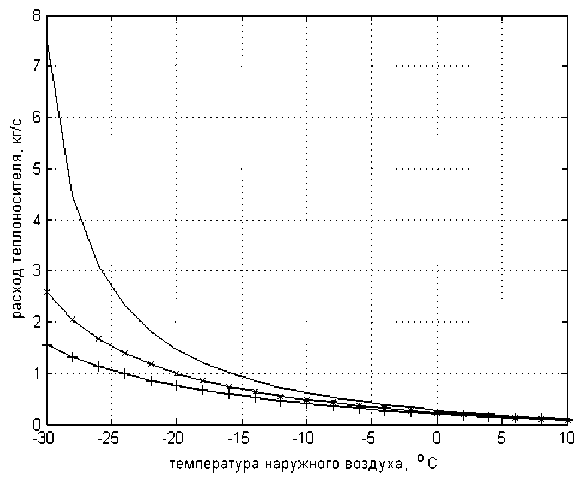
Рис. 1. Кривые изменения расхода теплоносителя в зависимости от температуры наружного воздуха

температуры наружного воздуха t_Н для 3 значений t_СО , считая снизу вверх: кривая 1 для t_cО = 120 ° С, кривая 2 для t_cО = 110 ° Си кривая 3 для t_cО = 100 ° С. При этом считалось, что t B = 18 ° С .

Как видно из рис. 1, при высоких наружных температурах расход теплоносителя практически не зависит от температуры воды на входе системы отопления tСО – все три кривые изображаются по существу одной и той же линией. Объясняется это, очевидно, низким уровнем теплопотерь здания. Кроме того, вполне понятно, что чем ниже tСО , тем больше должен быть расход теплоносителя на систему отопления.

Если подставить соотношение (3) в хорошо известную формулу для температуры обратной воды tОБР = t СО   V (tB - tH ) ,         (4)

cGСО то определим, что эта температура при регулировании по алгоритму (3) должна изменяться следующим образом:

^tОБР = - t СО ^{+ 2t}B ⁺ 7Т”7--^(tB - t H ).     ⁽⁵⁾

(kF)СО

На рис. 2 для условий рис. 1 приведены графики изменения температуры обратной воды, вычисленные по формуле (5).

Как это нетрудно видеть из рис. 2, регулирование по алгоритму (3) при некоторых наружных температурах недопустимо, более того, оно просто физически нереализуемо, так как согласно рис. 2 теплоноситель формально должен быть охлажден аж до отрицательных температур. К месту заме тим, что вероятнее всего по этой причине в работе

[1, с. 134] приведены уравнения эквивалента расхода воды и температуры обратной воды в зависимости от тепловой нагрузки только для случая, когда t_ОБ p >  t B . Для случая, когда это условие не выполняется, в [1] нет никаких рекомендаций.

Из всего вышеотмеченного, очевидно, следует, что использованные при выводе алгоритма (3) соотношения не учитывают условия физической реализуемости процесса отопления, поэтому нужна корректировка полученных решений.

На рис. 3 для t_cО = 100 ⁰ С приведены графики изменения расхода по соотношению (3) и из условия , что температура обратной воды в точности равна температуре внутреннего воздуха отапливаемых зданий. Как видно из рис. 3, при некоторых наружных температурах расход теплоносителя по алгоритму (3) меньше расхода, найденного из условия t_ОБ p = t B , следовательно, количественное регулирование по формуле (3) при таких наружных температурах в данном случае не является реально достижимым.

Покажем, какому неравенству должен подчиняться расход теплоносителя из условия, что температура обратной воды не может быть меньше температуры внутреннего воздуха отапливаемых зданий:

qVV З 1ОБР = 1СО        (1В	t H ) - t B ;	(6)
cGСО
З    q V V З tco tB -        (tB	- tH);	(7)
СО В cGСО В
G - q V V t B -	tН	(8)
иСО -      '	З. t B
c tСО

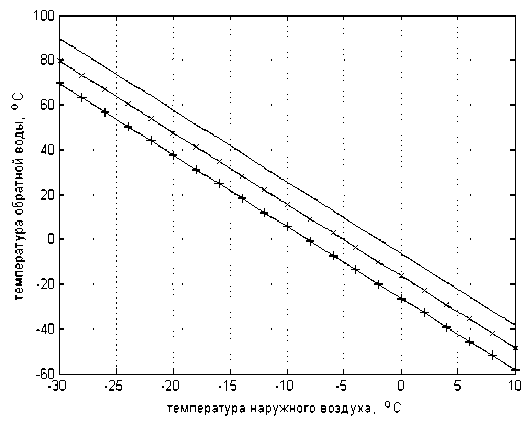
Рис. 2. Кривые изменения температуры обратной воды в зависимости от температуры наружного воздуха, вычисленные по формуле (5)

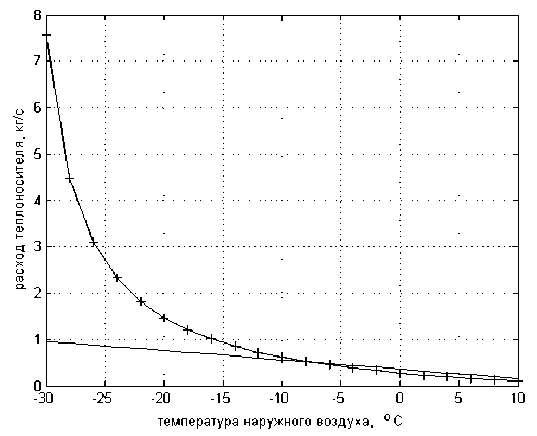
Рис. 3. Графики изменения расхода теплоносителя в зависимости от температуры наружного воздуха, вычисленного по уравнению (3),

З и из условия toБp = tB

Выясним, при какой температуре наружного воздуха отмеченные расходы будут равны. Как это нетрудно показать, это будет иметь место при следующей температуре:

t max = t 3 - ^О-^ _o-1 3 ).       (9)

Н В           СО В

2 ■ q v V

Для условий рис. 3 это будет наблюдаться при t_H =- 7,625 ° С . Кроме того, из формулы (9) сле-

(kF)

дует, что с увеличением параметра        крити-

2 ■ ’vV ческое значение наружной температуры, вычисляемое по формуле (9), уменьшается (смещается в сторону отрицательных наружных температур), т. е. диапазон наружных температур, при которых допустимо количественное регулирование по алгоритму (3), сужается.

Если учесть динамику процесса теплообмена (съема теплоты системой отопления с прямой воды), то, как это хорошо известно, система отопления конструируется так, что температура обратной воды должна быть заметно выше температуры внутреннего воздуха, в противном случае продолжительность процесса будет бесконечно большой. Обозначим разумный минимум температуры обратной воды через t^* , т. е. будем считать, что t_ОБ p >  t , тогда получим следующее соотношение для расхода теплоносителя:

G co > ^qVV-tM, .       (10)

^c   t co ^{- t}

На рис. 4 для t_co = 100 ° С приведены графики изменения расхода по соотношению (3) - отмечена плюсами и по границе неравенства (10), причем прямая, отмеченная звездочками, для случая, когда 1_ОБР = t В = 18 ° C , а прямая, отмеченная кружочками, когда 1_ОБР = t * = 30 ° C. Здесь равенство расходов по формуле (3) и для случая t_ОБР = t * = 30 ° C достигается уже при наружной температуре t_H =- 11,375 ° С .

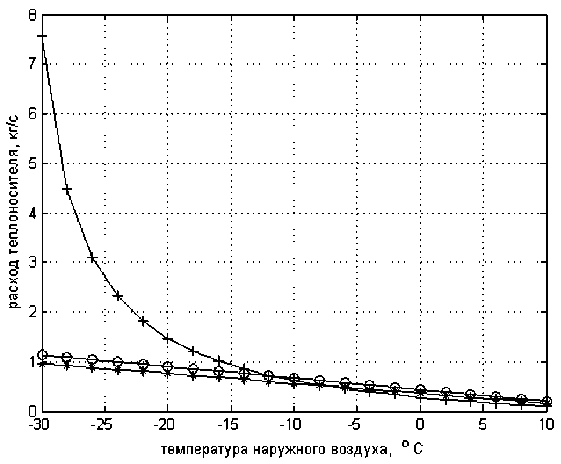
Рис. 4. Графики изменения расхода по формуле (3) и по границе неравенства (10)

Как видно из рис. 4, при увеличении t* диапазон наружных температур, в котором возможно количественное регулирование по алгоритму (3), заметно сужается.

Нетрудно показать, что равенство расходов по алгоритму (3) и по нижней границе неравенства (10) будет достигаться при следующем значении наружной температуры:

max t_Н

З

= ¹В

—

(kF) СО 2q V V

(tСО

+ 1 * — 2 ■ t В ).

Таким образом, учитывая вышеизложенное, алгоритм количественного регулирования можно представить следующей интервальной формулой:

GCО

= <

_______ ^qV^V(tB ¹Н⁾ ■ ^(kF)co _______

^2c[(kF)CO (^tco ^{— 1}В^{) — q}V^V(^tВ ^{— t}H^)]

З если 1н ^ 1g

(kF)СО

2 ■ qVV

(tСО

*

+ 1

^{— 2} ■ tB^);

^qV^{V (1}В ^{— 1}Н⁾ ----------------.--------------------------------- _*

c ⁽¹co ^{— 1} )

еслиtН

З   (kF)СО

> 1r

В 2 ■ qvV

⁽¹co ^{+ 1 — 2} ■ 4)

Температура обратной воды при этом будет изменяться следующим образом:

З   2qVV З                 З (kF)СО* З

— tco+2t +-- (t — t ), если t <  t--(t< o+t — 2 ■ t );

СО В          В Н ,      Н В           СОВ

(kF)СО2q

Лес™ ^tH >  ^tB ^— f) CO^(tco ^{+ t}* ^{— 2} ■ ^tB⁾.

2qVV

Однако при этом следует иметь в виду, что при регулировании расхода по второму интервалу будет наблюдаться завышенная мощность системы отопления, т. е. некоторый «перетоп». Так, например, температуре наружного воздуха t_H = 0 ° С теплопотери вышеуказанного здания при t g = 18 ° С будут составлять

123,84 кВт, а мощность системы отопления, вычисленная по расходу

Gco =

^qV^{V 1}b ¹h ---

*, c 1co —1

будет равна 159,167 кВт, «перетоп» 28,52 %. Понятно, что это приведет к увеличению температуры внутреннего воздуха, что может быть неприемлемым. В связи с этим количественное регулирование по первому интервалу будем называть идеальным.

Снижение температуры теплоносителя в подающей магистрали и расширение диапазона применимости идеального регулирования.

д tmax

Как это следует из соотношения (11) Н— < 0, д tCO т. е. с уменьшением температуры теплоносителя на входе системы отопления tСО верхняя граница применимости соотношения (3) для количественного регулирования растет и может оказаться так, что это уравнение применимо во всем практически значимом диапазоне наружных температур. Понятно, что в этом случае нет необходимости в использовании второго интервала алгоритма (12). Для примера на рис. 5 приведен график зависимости (11) для здания с qV = 0,86Вт/(м3 -°С), (kF)co = 4300 Вт/ °С, V = 8000 м3 при tВ =18 °С, toБР = t = 30 °C.

Как видно из рис. 5, при снижении температуры теплоносителя на входе системы отопления t_СО верхний предел применимости соотношения (3) для регулирования – t_Н ^max заметно растет и, например, при t_co = 50 ° С будет t m^ax = 4,25 ° С .

Таким образом, можно утверждать, низкотемпературное теплоснабжение и идеальное количественное регулирование (регулирование без «перето-па») органически (вполне естественно) взаимосвязаны, что при снижении температуры теплоносителя на входе системы отопления диапазон применимости такого регулирования расширяется. Вероятнее всего, по этой причине за рубежом применяют ступенчатое снижение температуры теплоносителя при регулировании процесса теплоснабжения за счет изменения расхода теплоносителя [3].

Некоторые замечания. Следует, однако, заметить, что предложенное решение задачи является достаточно общим, а не относится только к отоплению отдельного здания. Дело в том, что отопительную нагрузку как отдельного здания, так и некоторого микрорайона можно представить, как это неоднократно отмечалось в работах [10–14], как теплопотребление отдельного эквивалентного отопительного прибора. Также вполне понятно, что при конкретном применении алгоритма необходимо учитывать и допустимые температуры теплоносителя на входе систем отопления [9, 15]. Если же фактическая температура прямой воды выше допустимой, то необходимо также решить и задачу понижения этой температуры до предельно допустимого значения, что не рассматривается в данной работе. Вместе с тем предложенный алгоритм является практически значимым, так как представляет один из возможных вариантов ответа на вопрос о том, как конкретно следует изменять расход воды на отопление в вышеуказанной ситуации. Кроме того, в работе приведены достаточно подробные и, как нам представляется, вполне понятные обоснования полученных соотношений, что несколько проблематично, например, для работы [1]. Отметим также, что ответы на вопрос о количественном регулировании для несколько иных условий можно найти, например, в работах [16–20].

Выводы. Рассмотрено решение задачи количественного регулирования отопительной нагрузки зданий. Приведенный алгоритм детально обоснован и представляется двухинтервальной формулой по температуре наружного воздуха. Алгоритм характеризуется тем, что при регулировании на первом интервале потребителю в точности доставля-

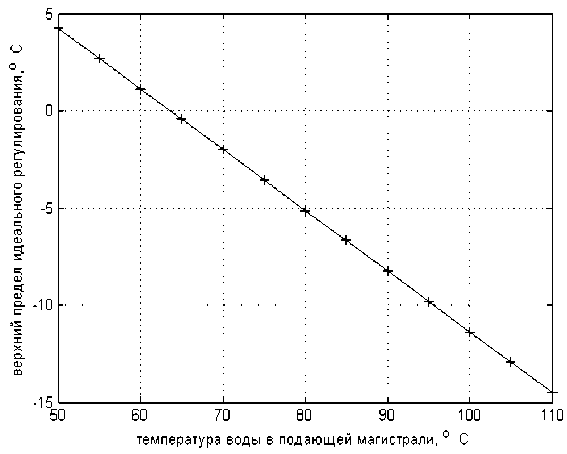
Рис. 5. График зависимости верхнего предела применимости идеального количественного регулирования от температуры теплоносителя в подающей магистрали

ется требуемое по погоде количество теплоты – регулирование идеальное. Однако на втором интервале – при высоких температурах наружного воздуха – количественное регулирование реализуется с некоторым «перетопом». Исклю- чить «перетоп» в этом случае можно за счет снижения температуры теплоносителя на входе системы отопления, так как в этом случае диапазон применимости идеального количественного регулирования расширяется.