К теории моделирования систем отопления

Рассматриваются варианты структуры математической модели отопительного прибора. Оценено качественное и количественное различие моделей. Отмечены специфические особенности моделей, позволяющие улучшить управление процессами системы теплоснабжения.

Вопросы создания математической модели отопительного прибора рассматривались в работах многих авторов. Так, в зависимости от способа определения его мощности (теплового потока) выделяют ряд функциональных зависимостей, составляющие параметры которых могут быть известны явным образом или определены с учетом некоторых допущений [1].

По-видимому, исторически первой математической моделью отопительного прибора является широко известное уравнение для определения его мощности:

д^К^вх^вых^Р, (1) где К и F - коэффициент теплопередачи и площадь поверхности отопительного прибора; ^ и 1_вых ~ температура теплоносителя на входе в прибор и выходе из него; t_e - температура воздуха в помещении.

Уравнение содержит как входные переменные ^ и /_в, так и выходную переменную 1_вых .

Следует отметить интересную особенность, что в литературе по расчету систем отопления неявным образом считается, что зависимость температуры теплоносителя от F является линейной функцией. На это указывает то, что среднее значение температурного напора для отопительного прибора принято вычислять по формуле:

. (2)

Формула (2) будет давать точное значение среднего температурного напора только в том случае, если температура теплоносителя вдоль F будет распределяться по прямой и будет при этом знакопостоянной функцией. В самом деле, хорошо известно, что средняя температура теплоносителя определяется по формуле:

г Q г г £

=0,5(Z +Z ), (3) где STP - площадь прямолинейной трапеции, образованной линейной знакопостоянной зависимостью t(F) и осью абсцисс на отрезке [0; F], что подтверждает справедливость вышеприведенного замечания по поводу вычисления AZ по формуле (2).

При расчете любого теплообменного аппарата неизвестные составляющие могут быть определены из уравнений теплопередачи или теплового баланса. Не является исключением и отопительный прибор, для которого

0,=^-^)»             (4)

где с и G - теплоёмкость и массовый расход теп лоносителя.

Таким образом, решая уравнения (1) и (4), найдем первый вариант структуры статической модели отопительного прибора, представляющий ся следующими уравнениями:

бы ~

cG(tM-te)

cG ’ 0,5 + —

KF

^вых ^вх

cG’

для которой на рис. 1 приведена структурная схема отопительного прибора.

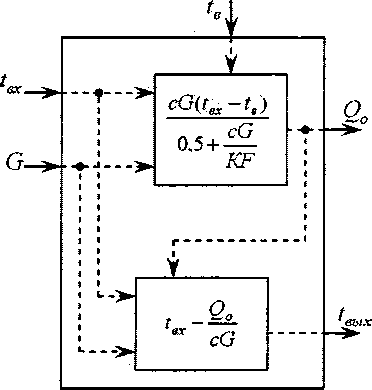
Рис. 1. Структурная схема статической модели отопительного прибора для системы уравнений (5)

На рис. 1 tex, te и G - входные переменные; при этом tex и G являются управляющими воз- действиями, соответственно t8 следует отнести к категории возмущений.

Для отыскания другого варианта структуры математической модели выделим бесконечно малый участок площади поверхности отопительного прибора и запишем уравнение теплового баланса для этого участка [2]:

-Gcdt = K(t-te)dF,

где t - температура теплоносителя в пределах участка dF.

Если считать коэффициент теплопередачи постоянным, то уравнение (6) будет представлять собой уравнение с разделяющимися переменными, которое можно представить в виде:

dtК

----=dF.

t-tgGC

Решая (7) с учетом того, что ДО) = ^, получим

( kfA

t(F) = tg +(/_ю-Q-exp -— .

V Gc j

Уравнение (8) описывает изменение температуры теплоносителя вдоль поверхности теплообмена при постоянном коэффициенте теплопередачи и если F вся поверхность теплообмена, то

Используя уравнение (8), нетрудно найти выражение для мощности отопительного прибора, очевидно, что это величину следует определять по уравнению:

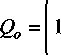
KF '

CG CG^-tg).

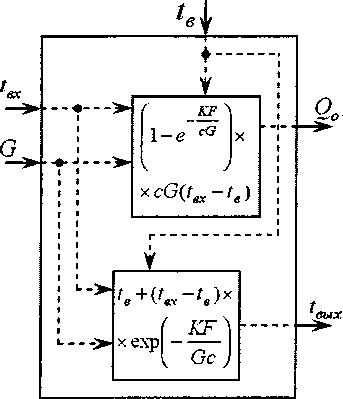
Рис. 2. Структурная схема статической модели отопительного прибора для системы уравнений (9)

Таким образом, второй вариант структуры статической модели отопительного прибора представляется следующими уравнениями:

Q_o2= 1-/^ CG^-tgY, X       7

/ х ( KF ^вых — ^в* (Jex ^в )" exp

Структурная схема модели отопительного прибора в этом случае представлена на рис. 2.

С другой, стороны из теории рекуперативных теплообменных аппаратов (ТО), работающих, например, по схеме «противоток», известно, что мощность теплообменника следует вычислять по формуле:

Qmo = 8-cGx(tXex -t2ex), где rlax и t2ex - температуры первичного и вторичного теплоносителя на входе в теплообменник; cGx - эквивалент расхода первичного теплоносителя; в - коэффициента эффективности ТО, определяемый по формуле:

1 _ ^ LcG2 J l-^Le^b0! J cG2

где cG₂ - эквивалент расхода вторичного теплоносителя.

Применительно к отопительному прибору следует считать, что cG_x - эквивалент расхода воды, протекающий через прибор ( cG ), a cG₂ - эквивалент расхода воздуха, омывающего отопительный прибор, который во много раз больше cG_x . Учитывая это, получим выражение для коэффициента эффективности ОУ:

KF е_о=1-е ^с<3

(И)

Параметр е_о позволяет определять мощность ОУ через большую разность температур теплооб-менивающихся сред

Qo ^{= Е}О " ^С^(1вх ~tg^ , (12) откуда совместное решение с уравнением (11), позволяет получить зависимость, полностью совпадающую с уравнением статики (9):

7 -—)

бог = 1-^{е cG} cG^-tg).

X 7

Уравнение (9) удобно использовать для расчета конкретного отопительного прибора. Если же рассматривать в целом всю систему отопления, то удобно перейти к параметрам теплоносителя в тепловой сети, так как температурный график в наружных сетях обычно выше, чем установленный для отопительной установки (ОУ). Поэтому структуру модели (9) на рис. 2 можно дополнить схемой узла смешения (рис. 3).

Э

tex

(Г

Рис. 3. Схема узла смешения перед системой отопления

знать только установленные входные параметры и значение коэффициента смешения.

Для получения третьего варианта структуры статической модели отопительного прибора учтем зависимость коэффициента теплопередачи от среднего значения температурного напора и расхода. Как известно [4] эта зависимость имеет вид:

К = mMnGp,

На рис. 3 смесительным устройством является водоструйный элеватор (Э), перед которым «средствами автоматики» [3] установлен расход сетевой воды G_c с температурой г_{ет с} > . Физический смыл перехода с температурного режима наружных сетей на температурный график системы отопления определяется через уравнение неразрывности струи посредством вычисления коэффициента смешения

где т, п и р - экспериментальные числовые показатели, зависящие от типа прибора и характера циркуляции в нем воды; М - текущий температурный напор; G - относительный расход воды.

Подставив соотношение (20) в уравнение (6), а затем, проинтегрировав, найдем выражение для вычисления текущего температурного напора отопительного прибора:

_ Авх с-^х _ G-G₍ ^ВХ ^—^вых G_c

Выразим температуру воды на входе в ОУ t_ex через коэффициент смешения с учетом (5)

t =t -и— cG подставив которую в (5) для QoX получим следующую модификацию уравнения статики, позволяющую находить мощность отопительного прибора через разность температур теплообменивающихся сред:

M = t-te = \—GpF + (t„-tyn ”. \Gc J

Откуда зависимость температуры теплоносителя от площади поверхности F, очевидно, будет представляться следующим уравнением:

t(F) = te + — -GpF + (t -t yn "

Q_o = e_ocGexjc-t_eY откуда коэффициент эффективности равен

0,5 + и ч-- KF

При совпадении установленных температурных графиков в системе отопления и тепловых сетях необходимость устройства узла смешения отпадает, то есть и = 0, тогда коэффициент эффективности примет вид:

KF

откуда ясно, что при подстановке (16) в (12) также прейдем к виду структуры статической модели (5).

Из рис. 3 и уравнения (13) следует, что G = (1 + u)G_c . С учетом этого мощность ОУ можно представить следующим выражением:

позволяющим определить /_вых при конкретном значении F.

В работе [2] построены кривые распределения температуры теплоносителя вдоль площади поверхности отопительного прибора для различных значений расхода, из которых видно, что формулы (8) и (21) дают практически одинаковое распределение температуры теплоносителя вдоль поверхности теплообмена. Различие становится существенным только при больших значениях F и малых значениях расхода теплоносителя.

Формулы (8) и (11) точнее учитывают физику процесса, поэтому предпочтение следует отдавать данным соотношениям, чем общепринятому положению о том, что распределение температуры теплоносителя вдоль поверхности отопительного прибора имеет линейный характер [4].

С помощью уравнения (21) можно получить третье уравнение статики для определения g,:

Qo^o-cGAtexc-V)’ где коэффициент эффективности равен

(17) соответственно

Qo = cG tex-te-\—-GpF + (tex-tey \Gc

о

0,5 + и cG_c

Таким образом, третий вариант структуры статической модели отопительного прибора представляется следующими уравнениями:

1 + и KF

Таким образом, для систем отопления, подключенных по зависимой схеме с температурным графиком ниже, чем в тепловой сети удобно использовать уравнение (17) для определения мощности системы отопления в целом, где достаточно

^^cG 1вх-1в-\^-.ОрЕ + ^-^

Gc

1вых = te + — ■ GpF+(^-tey" \Gc

Структурная схема модели отопительного прибора в этом случае представлена на рис. 4.

Для вычисления второго предела функции применим правило Лопиталя

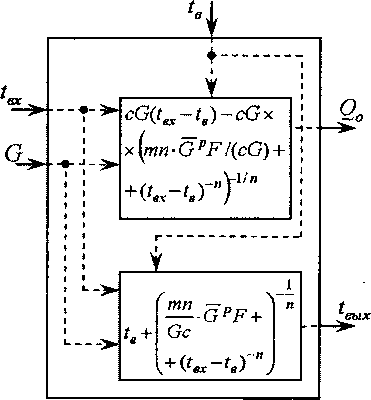
Рис. 4. Структурная схема статической модели отопительного прибора для системы уравнений (22)

lim

Л'-Х+О

1-е

0,5^ + 1

■ = lim ■

е

1 (0,5А + 1)2

= 1- (25)

Таким образом, график функции (йд/йя)= /W будет иметь вид, приведенный на рис. 5.

Вместе с тем интересно также оценить и количественное различие моделей. Для примера рассмотрим структуры модели из уравнений (5) и (9). Откуда видно, что отношение мощностей отопительного прибора QoijQox определяется следую

щим выражением:

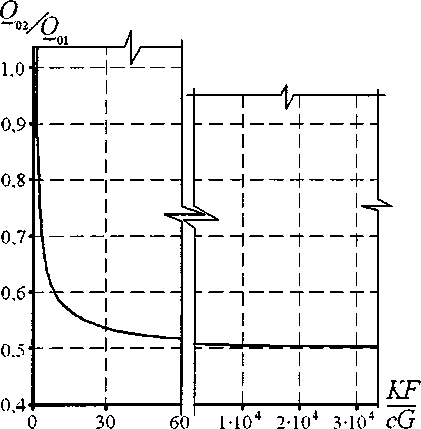
Рис. 5. Графики функции Qo2/Qo1

бо2 .

бо1

1-е

KF '' cG

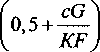
Как видно из (23) отношение мощностей является функцией параметра KF/(cG) . Представим

последний за X и исследуем поведение функции QoijQoi в зависимости от X, для чего проведем прямые вычисления (см. таблицу).

Результаты вычислений Q_o2/Q_oi по формуле (23)

Qoi/Qox	0,999992	0,694934	0,599873
KF/cG	0,01	5,01	10,01
Q02IQ0}	0,566622	0,549975
KF/cG	15,01	20,01
QoilQoi	0,50010	0.50005	0,50003
KF/cG	10000,0	20000,0	30000,0
QoilQox	0,50003	0,50002
KF/cG	40000,0	50000,0

Как видно из таблицы с увеличением параметра KF/cG отношение мощностей уменьшается.

Для построения графика функции 5_о2/й>1 ⁼Л^) найдем предельные значения этой функции при X стремящемся к бесконечности и к нулю справа:

lim ^2= Um о,5+—Н = 0,5. (24)

Из рис. 5 видно, при малых значениях параметра KF/{cG), то есть при больших расходах теплоносителя, варианты модели (5) и (9) практически равноценны. При больших значениях этого параметра, имеющих место, очевидно, при малых расходах, мощность отопительного прибора, вычисленная по второму варианту структуры будет в 2 раза меньше, чем мощность найденная по первому варианту структуры. Поэтому при прочих равных условиях температурные графики регулирования, построенные на основе первого варианта, уравнение (5), будут располагаться ниже графиков, построенных на основе второго варианта -уравнение (9). А поскольку физика процесса теплопередачи точнее учитывается вторым вариантом модели чем первым, то теплоснабжение зданий, рассчитанное на основе первого варианта модели (в настоящее время используется именно этот подход) будет приводить к тому, что количество доставленной потребителю тепла не восполнит его тепловую потребность, обусловленную потерями тепла через ограждающие конструкции.

Анализ данных работы [2] говорит о том, что графики распределения температуры теплоносителя вдоль поверхности теплообмена F , вычисленные по второму, и третьему вариантам структуры математической модели, практически одинаковы и, очевидно, что при использовании этих структур

погрешность в определении теплоотдачи отопительного прибора будет менее значимой.

Вместе с тем это не означает, что одинаковыми будут и вычисленные значения мощностей Q_o2 и g_o3, - формулы (9) и (22), поэтому необходимо выяснить какое количественное различие дают эти формулы.

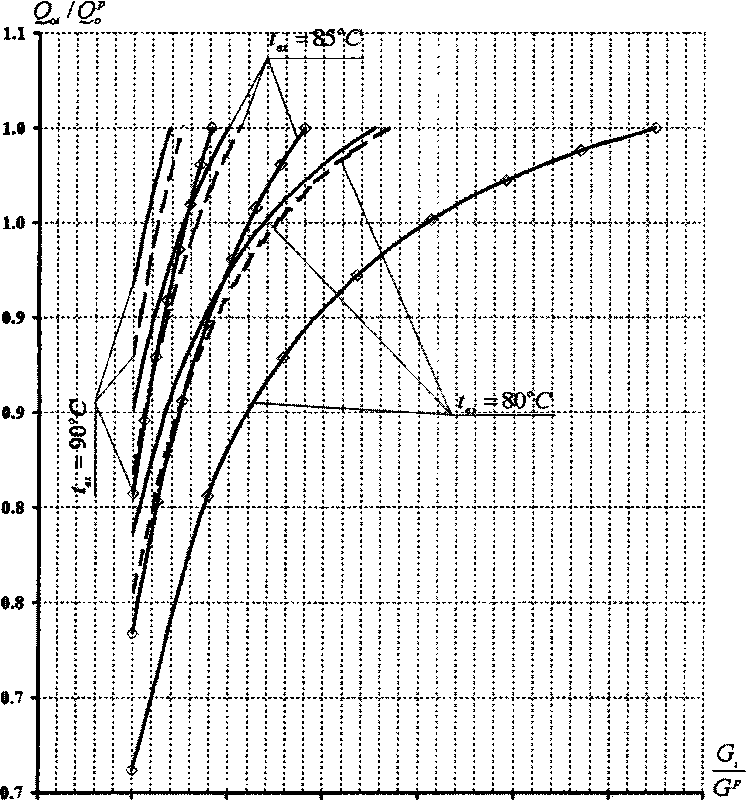
На рис. 6 приведены графики для относительных значений мощностей отопительного прибора, определенные по всем трем вариантам структуры математической модели для различных входных температур теплоносителя (80, 85 и 95 °C). Указанные на рис. 6 кривые позволяют провести анализ по сходимости результатов расчета между структурами уравнений (5), (9) и (22).

За базовое (расчетное) значение мощности Qp отопительного прибора использовалась величина 1536 Вт, найденная стандартным образом [4] для 10-секционного отопительного прибора М 140 АО. Здесь индекс i означает номер варианта структу ры. За базовое (расчетное) значение расхода Gp была взята величина 0,015 кг/с, температурный график 95-70 °C.

Расчет проводился методом последовательных приближений путем увеличения расхода теплоносителя и нахождения Q_m - до достижения величины, отвечающей значению Q^p . Подписи осей абсцисс и ординат обусловлены отношением текущего значения к расчетному, соответственно мощности отопительного прибора и расхода теплоносителя.

Так, сплошные кривые построены по первому уравнению статики (5), пунктирные по второму уравнению статики (9), а сплошные кривые, обозначенные «ромбами», по третьему уравнению статики (22).

Как видно из рис. 6 сплошные и пунктирные кривые практически схожи при данных значениях температуры теплоносителя на входе в отопительный прибор. Такая близость справедлива, так как в

ФЛ

5Л

«Л

Рис. 6. Кривые изменения мощности отопительного прибора от расхода для различных значений входной температуры теплоносителя

структуру уравнений (5) и (9) входит коэффициент теплопередачи, изменение которого не учитывается.

В то же время, кривые, построенные по уравнению (22) отличаются от остальных и учитывают изменения коэффициента теплопередачи во всем диапазоне регулирования. Наиболее явно различие просматривается при значительном снижении t_ex, например до 85 °C, когда для достижения расчетного значения мощности расход необходимо увеличить в 6 раз.

Выводы

Из структурных схем математической модели отопительного прибора видна близость уравнений статики для первого и второго варианта, соответственно по сравнению с третьим вариантом. Причем в большей степени она определяется постоянством значения коэффициента теплопередачи.

Вместе с тем практическая значимость определяется включением в искомые уравнения расчетных значений расходов. В этом случае количественное различие между первым и вторым вариантами становится существенным.

Также видно, что при высоких входных температурах и практически реальных диапазонах измене ния расхода мощности Qo2 и Qo3 практически одинаковы. Следовательно, при управлении процессом теплоснабжения необходимо учитывать и эту особенность, в частности, при качественно-количественном регулировании, и установить целесообразность использования первого варианта структуры статической модели отопительного прибора.