К теории переопределенных систем интегральных уравнений типа Вольтерра с особыми линиями

• 1.    Введение

• 2.    Основной результат

Отметим, что изучению интегральных уравнений и краевых задач для аналитических функций посвящены известные монографии Н. И. Мусхелишвили [1], Ф. Д. Гахова [2], И. Н. Векуа [3]. Достойный вклад в развитие теории интегральных уравнений с непрерывными ядрами, со слабо-сингулярными ядрами, многомерных интегральных уравнений внес труд С. Г. Михлина [4]. Работы А. Джураева [5], Г. Джангибекова [6] и их учеников посвящены изучению обобщенных аналитических функций, также связанных с ними двумерных сингулярных интегральных уравнений. Исследованию характеристического сингулярного интегрального уравнения с ядром Коши в исключительном случае, получению условия разрешимости и явной формулы представления решения посвящена

работа А. П. Солдатова [7]. Теория сингулярных интегральных уравнений с особенностями логарифмического или степенного типа, а также одновременно со слабыми и сильными особенностями в различных сочетаниях, была разработана Н. Б. Плещинским [8]. Основам вычисления определенных, сингулярных и гиперсингулярных одномерных и двумерных интегралов, а также численному решению уравнений с ними, построению и обоснованию вычислительных схем решений для слабо-сингулярных и сингулярных интегральных уравнений различных видов посвящены труды С. А. Довгого, И. К. Лифанова [9], Г. А. Расолько [10] и И. В. Байкова [11].

Отметим, что ранее в работах Н. Раджабова [12] были исследованы интегральные уравнения типа Вольтерра с особыми левыми и правыми граничными, а также внутренними сингулярными или сверх-сингулярными ядрами. Изучению переопределенных систем одномерных интегральных уравнений типа Вольтерра с сингулярными или сверхсингулярными точками в ядре посвящена монография [13]. В [14] исследованы двумерные интегральные уравнения типа Вольтерра с особыми и сильно-особыми граничными линиями в прямоугольнике. Работы [15–17] посвящены изучению двумерных интегральных уравнений типа Вольтерра с особыми и сильно-особыми граничными линиями по одной из переменных и слабо-особыми линиями по второй переменной на полосе. В данной статье исследуется переопределенная система интегральных уравнений, которая состоит из одного двумерного и двух одномерных интегральных уравнений с особыми линиями. Для этой системы уравнений получены явные решения, которые могут содержать произвольные постоянные, определены условия совместности уравнений системы, изучены свойства решений, а также выписываются решения соответствующих задач типа Коши.

Пусть дан прямоугольник D = {(x,y) : a < x < ai, b < y < bi} с граничными линиями Г1 = {y = b, a < x < ai}, Г2 = {x = a, b < y < bi}. Рассмотрим в нем переопределенную систему интегральных уравнений с особыми линиями вида x u(x,y) + A f ut-a)

a x 7,  4

< u(x,y)+ v f -—£■ a b u(x,y) - X f

y

b     xb uxs   -E t dt  uML dt - I1 J b-s ds + ° Jt-aJ b-s ds = f (x,y), dt = gi(x,y)

ds = g 2 (x,y)

где f , g i , g2 — заданные функции, A, у, 5, v, x — заданные числа, u — искомая функция.

Решение переопределенной системы интегральных уравнений типа Вольтерра с особыми ядрами (1) будем искать в классе функций u G C (D), обращающихся в нуль на Г 1 и Г 2 с асимптотическим поведением:

u(x,y) = o[(x — a)^£], е >  0, x ^ a, u(x, y) = o[(y — b) ^£ ], e> 0, y ^ b.

Будем говорить, что в системе (1) основным уравнением является первое, если сначала находится его решение, а после подчиняется второму и третьему уравнению.

Аналогичным образом вводится понятие основного второго и третьего уравнений.

Отметим, что если в системе интегральных уравнений (1) основным уравнением является первое, то функция f обращается в нуль на Г 1 и Г 2 с асимптотическим поведением:

f^{( x,} y) = o [^{(x —} a) ^{5 1}] ,

8 1 >  | Л | , при x ^ а,

f (x,y) = o [( b - y) ^Y1] ,

Тогда согласно [14], явное решение первого 8 = — Лц представимо в виде

Y 1 >  ц, при y ^ b.

уравнения системы (1) при Л < 0,

µ

> 0,

u^{( x} , y) = ^{( b —} yT^x^- + ^{( x —} aY^y) + ^{f (}x, y) ^{— Л} [ t — —a) x — a

^A fdt t — a

b

-1 (й)

y

^{1 f ( x,s )}

b — s

ds — Лц

a

/ ( t — a У d / ( ь — y Y J \x — aj t — aj \b — sj

f^ ds, b — s

a

y

где ϕ , ψ — произвольные функции.

Подставляя решение вида (4) во второе и третье уравнения системы, определяем условия совместности уравнений системы, значения произвольных функций в решении вида (4) для различных значений коэффициентов переопределенной системы (1). Для данной системы в случае, когда коэффициенты первого уравнения связаны между собой, справедливы следующие утверждения.

Теорема 1. Пусть в системе интегральных уравнений типа Вольтерра с особыми линиями (1) при соотношениях Л <  0 , ц >  0 , 8 = — Лц , v <  0 , х> 0 , | v | >  | Л | , f,g 1 ,g ₂ G C(D) f (a, b) = 0 с асимптотическим поведением:

f (x,y) = o (xx — a) ^{5 1}] , 8 1 >  | Л | , при x ^ a,

• ^f (x^ = o (bb ^— y ^{) Y1}] , Y 1 > Ц, ^пР^и У ^ ^b , существуют пределы

^{( b —} y^{) - 1} g i ⁽x,y) ^| y=b = g i ^{( x )},

(x — a) ^x g 2 (x, y) | x=a = g 2 (y)

причем g 1 (a) = 0, g 2 (b) = 0 с асимптотическим поведением:

• g i (x) = o (xx — a) ⁵ 2j, 8 2 >  | v | , при x ^ a,

• g 2 ⁽y) = o [^{(b —} y ^{) Y} 3] , Y 3 > x, при y ^ b.

При этом функции f, g 1 , g 2 связаны между собой условиями совместности

Xg '■ x y^- + (b ^— У ^у dx (g i (x,y^y — f (x,y^y + ( ^v _Л J (x - a^{- A}

X УФ(У)^ + 1» — У)(Л — v)Л [(x—a^A f dy                  J \t — a / t — a ds = 0,

a

Ag 2 (x, y) + XX - 1) (b — У) ^ ^^Л — v )(x — a)

x

^v c i + (A - v)g i (x)

t - a\g дУУ)            d

^{+ v (1 - A )} / X-^)    a ^{dt +( x - a )} ^^{g i ( x )}

a

b

∂

(x - a) — ∂x

\                  \ (b - У V f(x,s) J f (x,y)- g2(x,y) + (^ — x) / (b—s) ь - s ds

y где bχ

^(y) = (b - y)Xc2 + g2(y)+ x У ^b-s) g2-) ds- y

Тогда система (1) всегда разрешима и решение выражается равенством

u(x,y) = (b — УУ

(                      \       X X ^{x -} a) ^{| v |} g i ^{( t )}

(x - a) ci + gi(x) - v {----- -----dt t-a t-a

a

+(x - a) | ^{A |}

b

XX ^{b -} y) ^x g 2 ^{( s i}

^{( b -} y^{) X} c 2 + g 2 ⁽y⁾⁺ x   {b - s ) b - s ^ds

y

^{+ f ( x,} y) ^{- A}

x xt --aa λ

fw dt+ц b x   у fps. ds t-a           b-s b-s

y

t - a V dt f X b - У V f(t,s)

x-a t-a b-s b-s ay

a

x

-

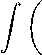
ds,

где c i , C 2 — произвольные постоянные.

Следствие 1. При выполнении условий теоремы 1 любое решение системы (1) из класса C(D) на r i и Г 2 обращается в нуль с асимптотическим поведением:

u(x, y) = o[(x - a) | ^{А |} ] , при x ^ a;

u(x, y) = o[(y - b) ^y 3 ], где У з = min(^, x) при y ^ b.

Свойство решения. Умножая на (b - y) ^{( -} ^) обе стороны полученного решения (13) системы (1), далее при ц < у, y = b, получим

⁽b ^- y) ^M u(x,y)\ y _{= b} =

(x - a) vci + gi(x) - v X Xx—a)  g^Xt) dt t-a t-a

a

Тогда

^{( x -} a)^{( b -} y ^{) -} ^ u ^{( x},y ⁾ | y _{= b} = c i . x=a

Теперь, умножая обе стороны решения (13) на (x - a) ^x , при | v | >  | A | , x = a, имеем

(x - a) ^x u(x,y) l _{x =} a = (b - y) ^x c 2 + g 2 (y)+ X I X b— ^y ) g ²— ds-b - s b - s

y

Тогда

⁽У ^{- b ) x ( x} — a^{) X} u⁽x,y⁾\ x=a, = ^c 2 . y=b

Теорема 2. Пусть в системе (1) при соотношениях Х < 0, ц > 0, 5 = X < 0, f,gi,g2 G C(D) f (a, b) =0 с асимптотическим поведением (5), (6) пределы (7), (8), где gi(x) = o [(x — a)£], е > 0, x ^ a;

—Хц, v >  0 , существуют

g2(y) = o [(y - b)£], е> о, y ^ b, а функции f, gi, g2 связаны между собой условиями совместности (11) и

x

Ag 2 ^{( x,}y)+ Ц — - ^( b - y) * (^A - ^{v )} g i ^{( x ) + ( v} - ^Хv ) У (~~)

At-)- dt +(x t - a

-

ч 9g i ^{( x ) a)}—

∂

= ⁽x ^{— a )} dx ^f (x’y)

-

a b

(    \          \ /(b— yV*f(x,s)л g2(x, y) + (ц — X)   I b—s ) b — s ds

y

.

Тогда система (1) всегда разрешима и ее единственное решение представимо в виде:

x

^u( x,y) = g i ⁽ x,y) ^{— v} У xj—^)

a xλ +f(x,y) — Х J (x—a) a x J(t—aVJLKb—y µ x-a t-a b-s

-

^{1 v |} g i (t)

t

- a

^f (t,y)

t -

a

a

b d + g2(x,y)+ х У У-—s)

y

b d+y/Ai)

y

b

* f^{( x,s )}

b - s

* f (t,s) , ds. b - s

y

^X g 2 (s) , ds b - s

ds

Следствие 2. При выполнении условий теоремы 2 любое решение системы (1) из класса C (D) на Г 1 и Г 2 обращается в нуль с асимптотическим поведением:

u(x, y) = o[(x — a) ^£ ] при е >  0;

u(x, y) = o[(y — b) ^£ ] при е >  0.

Теорема 3. Пусть в системе (1) при соотношениях Х <  0 , ц >  0 , 5 = — Хц. v >  0 , X > 0 , f,g i ,g 2 G C(D) f(a,b) =0 с асимптотическим поведением (5) , (6) существуют пределы (7) , (8) , где g i (a) = 0 , g 2 (b) =0 с асимптотическим поведением (14) , (10) . Функции f, g i , g 2 связаны между собой условиями совместности (11) и

^Х g 2 ^{( x}, У) + Ц— - 1^ ^{( b} - yY ^{( Х} - ^v)g 1

x + v (1 — Х) J (t V gi^ dt + (x — a)^^ x - a t - a           ∂x

— (x —

^{a )} ds ^f^у)

-

a b b - g2(x,y) + (Ц - X)   I b—)

y

* f ^{( x,s )}

b - s

ds

.

Тогда переопределенная неоднородная система интегральных уравнений типа Вольтерра с особыми линиями (1) всегда разрешима, решение содержит одну произвольную постоянную и представимо в виде:

x

u^{( x,} y⁾ = ^{( b} - у) * g i (х)

-

ν

Ях — a\ t-a

| ν |

g i ⁽t

t

-

a

dt

a

b

+(х — a) ^{| A |} (b — у) ^х С 2 + g 2 (y) + x

y

^b b - ^y s

^х g 2 (s)

b

-

s

ds

x

^{+ f ( х,}у) - A

a

_xt -_- a_a

λ

f ^{( t,} y)

t

-

a

dt + g

x

b

b

y

^b b - ^y s

* f ^{( x,s )}

-

λµ

a

t - a ^λ dt b - y x - a t - a b - s

y

b

-

s

ds

* f (t,s)

b

-

s

ds.

Следствие 3. При выполнении условий теоремы 3 любое решение системы (1) из класса C(D) на Г 1 и Г 2 обращается в нуль с асимптотическим поведением:

u(x, у) = o[(x — a) ^£ ] при е >  0;

u(x, у) = o[(y — b) ^Y 4 ], где Y 4 = тш(д, х) при у ^ b.

Свойство решения. Умножая обе стороны решения (16) на (х — a), при |v| > |A|, х = a, получим bχ

^{( х —} a^{) X} u⁽x,y)\ _x = _a = ^{( b —} y^{) x} c 2 + g 2 ⁽y)+ x J by — 7^) g y — y ^ds - ^y

Тогда

⁽y - ^{b ) X (x} - ^a )^Xu^{( x,} y)\ x=a, = ^c 2 - y=b

Теорема 4. Пусть в системе (1) при соотношениях A < 0, g > 0, 6 = —Xg, v < 0, X < 0, |v| > |A|, f,gi,g2 G C(D) f(a,b) = 0 с асимптотическим поведением (5), (6) существуют пределы (7), (8), где gi (a) = 0, g2 (b) = 0 с асимптотическим поведением (9), (15). Функции f, gi, g2 связаны между собой условиями совместности (11), (12), где bχ

Ш= . ^х / by У^ ds.

y

Тогда переопределенная система (1) всегда разрешима, решение содержит одну произ- вольную постоянную и выражается равенством

x

u(x,y) = (b - уУ

(x — a) ^v c 1 + g 1 (x)

-

ν

a

x - a t - a

| ν |

«44 dt t-a

+(x — a) ^{| A |}

^{+ f ( x,}y) ^— A

- λµ

f(ь—yYg2(sY g2(y) + XJ . ..) ds y

x xt --aa λ

a

fty)

t - a

d_{t +} > / ( b — y у YxY b - s b - s

y

ds

/ (t—aV "'   (ь—yу x-a t-a b-s

f Уз) b - s

ds.

a

y

Следствие 4. При выполнении условий теоремы 4 любое решение системы (1) из класса C(D) на Г 1 и Г 2 обращается в нуль с асимптотическим поведением:

u(x, y) = o[(x — a) ^{| A |} ] , при x ^ a;

u(x, y) = o[(y — b) ^£ ], e >  0 при y ^ b.

Свойство решения. Умножая на (y — b) ^- ^ обе стороны полученного решения (17) системы (1), при выполнении условия (b — y) ^- ^ g 2 (y) l y=b = 0, при x = a, получим

x

⁽ b ^— y) ^M u(x,y)| y _{= b} = ⁽x ^— a) ^v c i + g i ^{( x )}

-

ν

a

x - a t - a

| ν |

®4> dt t-a

Тогда

^{( x —} ay^{( b —} y) ^{- u (} x,y ⁾ | y=_f = c l .

x=a

Теорема 5. Пусть в системе (1) при соотношениях A > 0 , ц <  0 , 5 = — Ху. f,g i ,g 2 € C(D) f(a,b) = 0 , g i (a,b) = 0 , g 2 (a,b) = 0 , соответственно, с асимптотическим поведением:

f (x, y) = o (xx — a) ^£] , e >  0 при x ^ a; (18) f (x,y) = o[(y — b) ^£ ], e> 0 при y ^ b, (19) g i (x,y) = o [( x — a) ^£] , e> 0 при x ^ a; (20) g i (x,y) = o[(y — b) ^£ ], e> 0 при y ^ b, (21) g ₂ (x,y) = o(x — a) ^£] , e> 0 при x ^ a; (22) g 2 (x,y) = o[(y — b) ^£ ], e> 0 при y ^ b. (23)

Функции f , g 1 , g 2 связаны между собой условиями совместности:

\ r f (t— a V f(t,y)   x f(b — yY f(x,sY f (x, y) — (v — A)    ----- -----dt + ц ---- —----ds x-a t-a           b-s b-s ay x f (t— a Y dt f(b—y Yf(t,sY     ( \

+ц(v — A)  {--- 7— /7—  т—ds = gi(x,y), x-a t-a b-s b-s ay

f ^{( x,} y) - A

x xt --aa λ

a

f (t,y) t - a

b dt ■ .-x)/(b s)

y

fxs) b - s

ds

b

+ ^{a (} X - д)

X ( t - a V JL [ ( b - У \ x - a t - a b - s

a

y

µ

f ^{( t,s )} b - s

ds = 9 2 (x,y)-

Тогда переопределенная система (1) имеет единственное решение, представимое в виде:

^{и ( х,} У⁾ = f (^ У) - ^А

x xt --aa λ

a

f (t,y) t - a

b

-                '

y

fxs) b - s

ds

b

- λµ

X ( t - a V JL [ (b - У \ x - a t - a b - s

a

y

µ

f УУ b - s

ds.

Следствие 5. При выполнении условий теоремы 5 любое решение системы (1) из класса C(D) на Г 1 и Г 2 обращается в нуль с асимптотическим поведением:

u(x, y) = о У — а)У , £ > 0 при x ^ a;

u(x,y) = o[(y — b) ^£ ] , £ > 0 при у ^ b.

Теорема 6. Пусть в системе (1) при соотношениях A > 0 , д >  0 , v < 0 , 5 = — Ад , f,g i ,g 2 € C(D) f (a,b) =0 с асимптотическим поведением (6) , (14) , существует предел (7) , где g i (a) =0 и g 2 (a,b) = 0 удовлетворяют (9) , (22) , (23) , соответственно. Функции f , g 1 , g 2 связаны между собой условиями совместности:

Д9 1 ^{( х} ,У)+(Ь ^— У) dx

d Xf — — a\ ^A f(t,y)

9i(.x,y) - (f^{( х} ,у))+^{( А — v )( b —} y)^- / 7---- -7— —dt

= 0 , (24)

∂x t - a t - a

a g2(x,y) = ^1 — Д^ (b — yY (x — a)

^v c i + g i (x) + v 1 (—X gl^ dt x - a t - a

a

xλ

+f (x,^{y) — A} J (^) a

f^ dt + (Д — X) / (b У ft^ t - a                 b - s b - s

y

ds

~^A( — ^— X)

^{J (} t — a у dt } ⁽ b — у V x - a t - a b - s

fxs) b - s

ds.

ay

Тогда неоднородная система (1) всегда разрешима, решение содержит одну произволь- ную постоянную и выражается равенством

x x - a\|v| дУУ)

u(x,y) = (b - УУ

(x - a) C1 + gi(x) - V ---- ----ddt t-a t-a

a

^{+ f} У,У) ^- A

x xt --aa λ

a

f Уу) t - a

dt + ц f (У f b-s b-s y

ds

- λµ

/ ⁽ ' "  V JL / ⁽ b - У Y x - a t - a b - s

f Уз) b - s

ds.

a

y

Следствие 6. При выполнении условий теоремы 6 любое решение системы (1) из класса C(D) на Г 1 и Г 2 обращается в нуль с асимптотическим поведением:

u(x, y) = o[(x — a)^£], е >  0 при x ^ a;

u(x, У) = o[(y — b)^] при У ^ b.

Свойство решения. Умножая на (у — b) ^ обе стороны полученного решения (25) системы (1), при выполнении условий теоремы 6, при у = b, получим

x

⁽b ^— у) ^ u^{( x} ,y⁾\ _y =b =

x — a\ ^{| v |} 91У)

(x — a) ci + gi(x) — v ---- ----ddt t-a t-a

a

Следовательно, (x — a)(b — y) ^ u(x,y)\ _y =b = c ₁ -

Теорема 7. Пусть в системе (1) при соотношениях A > 0, ц > 0, V > 0, 6 = —Хц, f,gi,g2 € C(D) fУУ) = 0 с асимптотическим поведением (18), (6), существует предел (7), где g1(a) = 0 и g2(a,b) =0 удовлетворяют формулам g1(x) = o[(x — a)], е > 0, при x → a, и (22), (23), соответственно. Функции f, g1, g2 связаны между собой условиями совместности (24) и x

■■ ^{у )} = (1 ^— ц ) [^{g i} (x, ^{у ) — V} / (x — a) g y ^dt]

a xb +f(x,y)—A/(xa) f^dt+(ц—x)/(b—y)

ay

-Ц— - X) I ( xr^ ) A / () ' A ds.

t - a t - a b - s b

-

- s

a

y

f У s')

b -

s

ds

Тогда неоднородная система (1) всегда разрешима и ее единственное решение выража- ется равенством

u(x,y)= 91(Х,У) - v [(x a}   gi(t,y dt t-a t-a

a

+f (x,y) - A 1 () A dt + * f (Ь-y)'      ds x-a t-a           b-s b-s ay x (t -a \A dt [(b - y }^f(t,s) j

• ^-λµ    x - a t - a b - s b - s ^ds.

ay

Следствие 7. При выполнении условий теоремы 7 , любое решение системы (1) из класса C(D) на Г 1 и Г 2 обращается в нуль с асимптотическим поведением:

u(x, y) = o[(x — a)^£], е >  0 при x ^ а;

u(x, y) = o[(y — ЬЛ при y ^ b.

Теорема 8. Пусть в системе (1) при соотношениях A < 0 , * <  0 , v <  0 , 5 = — A* , X > 0 , | v | >  | A | , f,g i ,g 2 G C (D) , f(a,b) =0 с асимптотическим поведением (5) , (19) , существует предел (x — a)g i (x, y} \ _{x = a} = g i (y), где g i (b) =0 и g 2 (a,b) =0 удовлетворяют формулам g i (y) = o[(y — b) ^£ ] , е >  0 , при y ^ b, и (22) , (23) , соответственно. Функции f, g 1 , g 2 связаны между собой условиями совместности:

(            1

g i ^{( x,} y) = a

∂ vf (x, y) — (x — a) dxtgdx, y) — f(x, y))

+*(x — a) ^ / (b-7Г ∂x b - s

y

^{f ( x,s} ) b - s

j        (b—y Vf(x,s ds + v*J (b—7) T—T y

ds,

b                                xλ g2(x,y) = gi(x,y) — x [ gYxs) ds + f (x,y) — A [ x——a) fYy- dt b-s                     t-a t-a ya

■ — X) i (b—yУ fxs1 ds + A(X — *) 1 ()A Л f (b—y У f s ds. b-s b-s                   x-a t-a b-s b-s y    ay

Тогда неоднородная система (1) всегда разрешима и ее единственное решение выражается равенством

( \                \ \ ¹ ( t ^{— a} V ^{f -,}у)Ъ+    У( ^{b —} yY ^{f ( x,s}Y

u(x,y) = gi(x,y) + f(x,y) — A/ ----- ----dt + */  7—   i----ds x-a t-a           b-s b-s ay

. [⁽t^{— a} V dt H^b — y V f ^{( t,s )}

• ^{- λµ} x - a t - a b - s b - s ^ds.

ay

Следствие 8. При выполнении условий теоремы 7 любое решение системы (1) из класса C(D) на Г 1 и Г 2 обращается в нуль с асимптотическим поведением:

u(x, y) = o[(x — a) ^{| A |} ] при x ^ a;

u(x, y) = o[(y — b) ^e ], e >  0 при y — b.

В случае, когда коэффициенты первого уравнения системы (1) не связаны между собой, т. е. 5 1 = 5 + Ху = 0 , решение переопределенной системы (1) будем искать в классе непрерывных функций, представимых в виде обобщенного степенного ряда:

∞

u(x, y) = (x — a) ^{- X} (y — bf ^(b — y) n^+Y U n (x).

n=0

Справедливо утверждение.

Теорема 9. Пусть в системе (1) при соотношениях Х <  0 , у >  0 , 5 1 = 5 + Ху = 0, 5 1 < 0, функции f, g i , g 2 представимы в виде:

∞ f (x, y) = (x — a)-X(y — b? £(b — y)n+Yfn(x), n=0

∞ gi(x,y) = (x — a)-X(y — by ^(b — y)n+Y gin(x), n=0

∞

92(x,y) = (x — a)-X(y — by ^(b — y)n+Yg2n(x), n=0

где f n , g in , g 2n € C (Г 1 ) , в точке x = a обращаются в нуль с асимптотическим поведением:

f n (x) = o

Y 1

| 5 1 |

>------, x —— a, n + Y

g 1n (x) = o[(x — a) ^e ], g 2n (x) = o[(x — a) ^e ],

e >  0, x ^ a,

e >  0, x — a.

Функции f n , g 1 _n и g 2n связаны между собой условиями совместности:

g 1n (x) = ^1 +

µ n + Y

) ⁽x ^— af n ^{( x ) — (}x ^— a^{) g} '1n ^{( x )+} (1 ^{— X + V} — V¹⁺        jf n^)x)

^{n            1n}                 n + Y n + Y

^— (¹⁺

µ n + Y

X ^X —^{V +} n+Y) (^l —

5 1 n + Y

x

Ж x — a) a

^ 1

^{n + Y} f n (t)

t — a

dt, n = 0, 1, 2, . . . ,

g 2n (x) = (n + Y + у — x)   1

—

V (n + Y )      9 1n (x)

X(n + y ) + 5 1 n + y + У

ν

⁺ X(n + y ) + 5 1

f n (x)

ν

+ v I -77-------7

\ ^X(n + Y )

—

+ 5 1    n + Y

x x — a

a

*i n+Y fn(t)

t — a

dtj ,     n = 0,1, 2,...

Тогда неоднородная система (1) в классе функций (26) , имеет единственное решение, представимое в виде

∞

δ

u(x,y) = (x — a) ^{- X} (y — by ^(b — y) ^n+Y (x — a) ^{n + Y} c,

^— (¹⁺

µ n + Y

n=0

x

\( 5 1 + X(n + y ) \ f ( t — a \

X \ n + Y X J \x — aX

a

‘ n — (1 + ^K(x) V ^{n +} yJ

^1 _{z x} ^{n + Y} f n (t) t — a

dt , n = 0, 1, 2, . . .

Причем, если существует предел (х — a) n +^Y g 2n (x)| x_a = с П , тогда c n определяется из равенства c n = ^^П^О^ ^V ) с П , n = 0,1,2,..., а при существовании предела 5 1

(х — a) ~g2n (x) = с П , С п определяется из равенства С п = ■Г+Гг - х с П ^п = 0,1, 2,...

Следствие 9. При выполнении условий теоремы 9 любое решение системы (1) из класса C (D) на Г 1 и Г 2 обращается в нуль с асимптотическим поведением:

u(x,y) = о [( х — а) ^{| Л |}] при х ^ a;

u(x, У) = о [(У — Ь)^м] при y ^ b.

Подобные утверждения получены и для других знаков коэффициентов системы интегральных уравнений (1), когда коэффициенты первого уравнения системы не связаны между собой. Явные представления многообразия решений и свойства системы интегральных уравнений (1) дают возможность для постановки и решения задач типа Коши, когда условия задаются на сингулярных многообразиях.

Задача K i . Требуется найти решение системы интегральных уравнений (1) из класса C (D) при А < 0, ц > 0, v < 0, 5 = — Ац, х > 0, | v | >  | А | , по граничным условиям:

^{( х} - a)⁽У - ^{b ) -} ■ ^{u ( x,} У) | _у__а, = A 1 ;

x _ a

⁽У - ^{b ) - x (}x - a) ^x u⁽x, у)| _y__a, = B i .

x _ a

Решение задачи K i . Пусть выполнены условия теоремы 1. Используя интегральное представление (13) и свойства решения, получим c i = A i , С 2 = B i .

Подставляя значения c i , С 2 в (13), имеем решение задачи K i . Следовательно, доказана следующая

Теорема 10. Пусть выполнены условия теоремы 1 . Тогда задача K i имеет единственное решение, представимое в виде (13), где c i = A i , С 2 = B i -

Задача K 2 . Требуется найти решение системы (1) из класса C (D) при А < 0, ц > 0, v > 0, 5 = — Ац, х > 0, по граничному условию (у — b) -^x (x — а) ^Л и(х, у) | _х__а, = B ₂ .

y_b

Решение задачи K 2 . Пусть выполнены условия теоремы 3. Используя интегральное представление (16) и свойства решения, имеем С 2 = B 2 .

Подставляя в (16) данное значение С 2 , получим решение задачи K 2 . Следовательно, доказана следующая теорема.

Теорема 11. Пусть выполнены условия теоремы 3 . Тогда задача K 2 имеет единственное решение, представимое в виде (16) , где С 2 = B i .

Задача K 3 . Требуется найти решение системы (1) из класса C(D) при А < 0, ц > 0, v < 0, х < 0, | v | >  | А | , 5 = — Ац, по граничному условию (х — a) ^v (b — y) - ^ u(x, y) | y_a, = A ₂ . x _ a

Решение задачи K 3 . При выполнении условий теоремы 4 и условия (b — у) - ^ g 2 (у)| y__a = 0, используя (17) и свойства решения, имеем c i = A 2 .

Подставляя в (17) данное значение c i , получим решение задачи K 3 . Следовательно, верно следующее утверждение.

Теорема 12. Пусть выполнены условия теоремы 4 . Тогда задача K 3 имеет единственное решение, представимое в виде (17) , где c i = A 2 .

Задача K 4 . Требуется найти решение системы (1) из класса C(D) при А > 0, ц > 0, v < 0, 5 = — Ац, по граничному условию (х — a) ^v (b — у) ^- ^ и(х, у)| _ь = A 3 .

^yx ^_ _ a^,

Решение задачи K 4 . Используя интегральное представление (25) и свойства решения при выполнении условий теоремы 6, имеем c i = A 3 .

Подставляя в интегральное представление (25) это значение c 1 , получим решение задачи K 4 . Следовательно, доказана следующая теорема.

Теорема 13. Пусть выполнены условия теоремы 6 . Тогда задача K 4 имеет единственное решение, представимое в виде (25) , где c i = A 3 .