К теории прямого межчастичного электро-гравитационного взаимодействия

В настоящее время в современной теоретической физике ведутся исследования в рамках трех физических парадигм [1]: доминирующей теоретико-полевой (классическая и квантовая теория поля), геометрической (общая теория относительности и ее геометрические обобщения) и менее известной реляционной . В рамках каждой из них по-своему представляется физический мир и его описание. По-видимому, наиболее полное представление о физической реальности можно получить, лишь умея взглянуть на нее с трех указанных сторон. Как нам представляется, значительные перспективы открываются в рамках именно реляционной парадигмы, основания которой были заложены в трудах Г. Лейбница, Э. Маха и некоторых других исследователей.

Исторически сложилось два основных подхода к пониманию природы пространства-времени. В наиболее привычном субстанциальном подходе физическое пространство-время мыслится как самостоятельная категория (субстанция), представляющая собой непрерывный фон, на котором развёртывается динамика погруженных в него частиц и полей. Наиболее четкое воплощение этот подход получил в рамках ньютоновской концепции абсолютного пространства и времени, а позднее был унаследован как в теоретико-полевой, так и в геометрической парадигме. В реляционном подходе пространство-время приобретает вторичный статус и трактуется как специфическая система отношений (relations) между объектами микромира; привычные макроскопические свойства пространства-времени порождаются ансамблями соответствующих материальных систем в усредненно-статистическом пределе, аналогично тому, как в термодинамических системах возникает понятие температуры. Таким образом, реляционный подход ставит задачу вывода закономерностей макроскопического пространства-времени из некоторых более фундаментальных характеристик микромира ³ .

Отказ от идеи гладкого пространственно-временного фона (многообразия) влечет трудности с определением классических полей-переносчиков взаимодействий как непрерывных функций на точках данного многообразия. Методологически это означает отход от концепции близкодействия в сторону концепции дальнодействия. На смену понятию классического поля приходит некоторая вторичная конструкция из характеристик взаимодействующих частиц, играющая роль эффективного поля.

По-видимому, исторически первой успешной попыткой реализовать концепцию дальнодействия, совместимую с требованиями релятивистской инвариантности, стала теория прямого межчастичного электромагнитного взаимодействия (action-at-a-distance), предложенная в ранних работах А. Фоккера, Х. Тетроде, К. Шварцшильда и позже усовершенствованная Р. Фейнманом и Дж. Уилером [2, 3].

В рассматриваемом нами реляционном подходе можно выделить две составляющие: 1) реляционное описание пространства-времени и 2) описание физических взаимодействий на основе концепции дальнодействия. Отметим, что в ХХ веке в работах Я. И. Френкеля, Р. Фейнмана, А. Фоккера, Дж. Уилера, Ф. Хойла и ряда других авторов развивалась именно вторая составляющая, которая оказывалась недостаточно обоснованной при игнорировании первой. В последнее время удалось существенно продвинуться в развитии реляционного подхода на базе математического аппарата теории систем отношений, основы которой были заложены в трудах Ю. И. Кулакова и его школы [4, 5]. Развитие первой составляющей реляционного подхода изложено в ряде наших работ [6–11].

В данной статье внимание будет сосредоточено на развитии второй составляющей с учетом достигнутых результатов в раскрытии реляционной природы пространства-времени. Демонстрируется ряд гипотетических результатов, касающихся природы электромагнитных взаимодействий и их роли в структуре физического мира. В частности, реляционный подход показывает, что гравитационное взаимодействие, обычно понимаемое как самостоятельный вид физических взаимодействий, может быть определенным образом истрактовано как своеобразное проявление электромагнитных взаимодействий, что созвучно, например, идеям академика А. Д. Сахарова о вторичной (индуцированной) природе гравитации. Важную роль при этом играет принцип Маха, понимаемый наиболее широко как зависимость локальных свойств физических систем от глобальных свойств окружающего мира.

Мы будем использовать уже ранее полученные результаты ряда авторов по описанию физических взаимодействий на основе теории прямого межчастичного взаимодействия типа Фоккера– Фейнмана–Уилера. Кроме того, мы будем применять математический аппарат развитой ранее реляционной теории (теорию систем отношений), за подробным изложением которой мы отсылаем читателя к [8]. Концептуальные основы реляционного подхода также изложены в [12, 13].

S^b

- e a e b

/ / 5(s ² (a, b))n ^_v dx ^ dx V

11 ^j (_a ) ^j ( b ) ^ 5^{(s 2 (a,}b⁾)^ds _a d^s b ,

(1.1)

где e _a и е ь - электрические заряды двух частиц, j ^a ) = e _a dx £ /ds _a — вектор, пропорциональный 4-току частицы с индексом a ; dx _a ^µ , dx _b ^ν – изменения координат; ds _a , ds b — смещения вдоль мировых линий частиц; n ^_v — метрический тензор пространства-времени Минковского; s ² (a, b) = (x ^ (s _a ) — x ^ (s b )) ² - квадрат интервала между точками на мировых линиях двух частиц, так что дельтафункция от s ² (a, b) представляется в виде:

5^{(s 2 (}a^,b)) = s^t^ - r ab ) =

i

2 | r ab |

[5⁽ct ab    r ab ) + 5^(ct ab + ^r ab ^)] -

(1.2)

Это означает, что при фиксированном положении частицы а в некоторый момент времени t o (на ее мировой линии) взаимодействие между частицами происходит при двух положениях второй частицы: в предшествующий момент t ⁰ (запаздывающее взаимодействие) и в будущий момент t ⁰⁰ (опережающее взаимодействие), соответствующих двум пересечениям световых конусов прошлого и будущего (с вершиной на мировой линии первой частицы в момент t o ) c мировой линией второй частицы.

Таким образом, согласно принципу Фоккера, запаздывающее и опережающее взаимодействия присутствуют симметричным образом. В 20-х – 30-х годах это представляло основную трудность теории прямого межчастичного взаимодействия. Можно было говорить о совпадении этой теории с общепринятой теорией поля лишь для статических и стационарных электромагнитных явлений. И лишь в 1945 году в работе Р. Фейнмана и Дж. Уилера [3] был устранен этот недостаток — было показано, что посредством учета окружающей материи (принципа Маха) опережающие взаимодействия исключаются, а запаздывающие удваиваются.

Как видно из формулы (1.1), в нее не входят поля переносчиков взаимодействий. Взаимодействие определяется лишь характеристиками частиц, то есть данной формулой описывается запаздывающее (и опережающее) дальнодействие на световом конусе.

Полное действие для системы взаимодействующих электрических зарядов в фоккеровской теории прямого межчастичного электромагнитного взаимодействия записывается в виде

S ^{( e )} =

m a c

a

ds

a

2c XX 11 j^j ( _b ) ^ 5(s²⁽a,by)ds_ads. ab

b ,

(1.3)

где m _a — масса покоя частицы a . Первое слагаемое справа соответствует действию для свободных (невзаимодействующих) частиц. Во втором слагаемом справа суммирование производится по всем парам заряженных частиц, причем a = b. Из этого выражения вариационным методом можно получить уравнения движения заряженных частиц в некотором эффективном поле A ff , удовлетворяющем уравнениям Максвелла в лоренцевой калибровке, что обеспечивает согласованность данной схемы с максвелловской картиной. После работ Фоккера, Феймана и Уилера рядом других авторов было показано, что весьма широкий класс классических линейных полевых теорий допускает эквивалентную фоккеровскую формулировку [14].

• 2.    Реляционная трактовка прямого межчастичного электромагнитного взаимодействия

Выражение (1.1) можно интерпретировать в терминах унарных систем вещественных отношений на множестве характеристик взаимодействующих частиц [8, 15]. Выделим здесь два класса таких отношений: ток-токовое парное отношение (между токовыми характеристиками) U ab = j aa y j b ) ^ и пространственно-временное парное отношение (между точками-событиями на мировых линиях) B ^b = 5(s²(a, b)). Представим подынтегральное выражение в (1.1) в символическом виде:

c ^{( e )}           Р⁾²^

(2.1)

S ( ab )     u ab B ab .

В последовательной реляционной теории, основанной на теории унарных систем вещественных отношений (УСВО) на некотором множестве элементов, каждый тип парных отношений характеризуется так называемым законом – функцией, обращающейся в нуль на произвольных r -элементных выборках внутри данного множества (число r носит название ранга данной УСВО) [8, 13]. Данная функция в простейших случаях сводится к формам объемов некоторых n -мерных симплексов в абстрактных (псевдо)евклидовых пространствах (такие объемы задаются детерминантами Кэли–Менгера или Грама).

Так, для токового парного отношения имеет место		соотношение:
Ф (5) =	e 2 U ab U ac U ba    ' 2 U bc U ca    U cb   ' 2	U ad   U al U bd    U bl U cd   U cl   = 0.                              (2.2)
	U da   U db   U dc U a   U b   U lc	e 2    U dl U ld    e 2

Данное выражение есть закон УСВО ранга 5, связывающий между собой все возможные парные отношения между 5 произвольными элементами (токами взаимодействующих частиц) и фактически являющийся определителем Грама на скалярных произведениях u ^a y u^p , равенство нулю которого отражает линейную зависимость любой выборки пяти 4-векторов.

От этого выражения можно перейти к определителю с единицами на главной диагонали посредством конформного преобразования величин uab. Конформные факторы разных элементов могут отличаться друг от друга лишь знаком [8] и (с точностью до размерного множителя) интерпретируются как электрические заряды идеализированных элементарных микрочастиц: uab = eaebuab.

В приведенных формулах стоят безразмерные величины. Для перехода к размерным зарядам предлагается использовать универсальные размерные физические константы, положив: е ² = е ² /( ~ c) = а, где ~ - постоянная Планка, е - элементарный заряд (электрона), а - постоянная тонкой структуры. Для получения действия в общепринятых единицах ~ представим подынтегральное выражение в (1.1) в виде

5 ( e) _ e a e b ц        _о(2)

^S ( ab ) = c u ( a ) ^{U ( b}> ^B ab ^{.                                         (}2.³⁾

Для второго парного (пространственно-временного) отношения, содержащего квадрат интервала s ² (a, b) между положениями двух частиц, закон записывается в виде равенства нулю определителя Кэли-Менгера, построенного на 6 элементах точках-событиях [8]. В данном случае достаточно использовать парное отношение в виде дираковской дельта-функции, B ab ) ^ 5(s ² (a, b)), которая означает, что подынтегральное выражение отлично от нуля лишь в случае, когда квадрат интервала между точками на мировых линиях взаимодействующих частиц равен нулю, что означает релятивистски инвариантное дальнодействие на световом конусе.

• 3.    Реляционное описание линеаризованной гравитации

Как было отмечено выше, в развиваемой реляционной модели фактически реализуется идея описания характеристик физических систем через некоторые геометрические инварианты — объемы симплексов в абстрактных линейных пространствах подходящей размерности. Так, в описании пространственно-временных систем отношений важную роль играют геометрические характеристики, связанные с определителями Кэли-Менгера, а также с его минорами, из которых строятся площади, объемы, значения углов, координаты и так далее. Аналогичным образом значимую роль при рассмотрении взаимодействий играют также миноры определителя (2.2) (см. [15]), выделение которых производится в ходе определенной процедуры декомпозиции исходного закона унарной системы вещественных отношений.

Из определителя (2.2) можно построить несколько видов миноров: три вида миноров второго порядка, три вида миноров третьего порядка и два вида миноров четвертого порядка, которые, как оказывается, имеют четкую физическую интерпретацию и играют важную роль в описании классических электромагнитных и гравитационных взаимодействий.

Так, представление (2.1) отвечает тому, что электромагнитное взаимодействие в фоккеровской форме определяется минорами первого порядка (то есть самими элементами) определителя (2.2).

Рассмотрим диагональный минор следующего, второго порядка в определителе (2.2). Так, для двух частиц, описываемых элементами a и b, можно определить парное отношение и прообраз взаимодействия:

_п(2) _   e ² uab ___.  5(g) _Г*п(2)р(2)                          (Ч 1

D ab =         22    --- > ^S ( ab ) = C 2 D ab B ab ,                         (3.1)

uba e где C2 - некоторая константа.

Поскольку здесь по-прежнему рассматриваются парные отношения элементов, то в формуле (3.1) следует ожидать прежнее выражение для координатного парного отношения B _a ⁽² _b ⁾ .

Расписывая (3.1) с учетом u ab = u ^a ) U ( b ) _M , можно представить соответствующий вклад в прообраз действия в виде:

5^(д) _    2 2^2 ^ц v (         |          _ 9         \ a J3                        Ч

^S ( ab ) = C 2 e a e b ^u ( _a ) ^u ( a ) ⁽ⁿ ^a ⁿ ve + ^п цР ⁿ va    2ⁿ ^v ⁿ a@ ^)u ( b ) ^u ( b ) B ab ,                 ⁽3.²⁾

где η µ_ν - метрический тензор пространства-времени Минковского.

Полученное выражение физически интерпретируется, исходя из его почти полного совпадения с действием фоккеровского типа для линеаризованной гравитации, ранее найденным в работах Я. И. Грановского и А. А. Пантюшина [16], а также некоторых других авторов4. В упомянутых ра- ботах было показано, что для линеаризованных гравитационных взаимодействий можно записать фоккеровское действие в виде, аналогичном (3.2), лишь с той разницей, что вместо токов взаимодействующих частиц следует писать их тензоры энергии-импульса. Раскрывая T µν для точечных частиц, имеем

^{S (} nt ^(a, ^b) = Gm a cm I I U ^a ) U ( a ) (n ^a n ve ⁺ 4^.n va

n ^v П ав ) u ab ) u ^e _b ) ^(s ² (a, b))ds a ds b ,       (3.3)

где u ^µ – компоненты 4-скоростей, а m – массы соответствующих частиц.

Выделим одну частицу с индексом a и произведем суммирование по всем частицам b. Добавляя свободное действие для частицы a, получаем для нее действие в форме

S a^g = —

cm a I 1 1 - G X h „v (a, b)u (_a ) u Va ) I ds a , \       b=a                     /

(3.4)

где использовано обозначение для потенциалов гравитационного воздействия на частицу a со стороны частицы b

0         mb h^v (a, b) = 2c,   6(s (a,b))(n^anve + П^вnva

ⁿ ^v ^п ав ^)u ( b ) ^U ( b ) ^ds b ^.

(3.5)

Объединяя вклады от всех частиц, имеем суммарный эффективный гравитационный потенциал в

месте нахождения выделенной частицы h „_v (a) = ^2b = a h ^_v (a, b).

Из действия (3.4) вариационным методом можно получить уравнение движения частицы в линеаризованном гравитационном поле, которое можно представить в виде линеаризованного уравнения геодезической. Легко показать, что метрика, определенная в виде g ^_v = n ^_v — h ^_v (a), удовлетворяет линеаризованному уравнению Эйнштейна [14].

Таким образом, диагональный минор второго порядка из закона (2.2) можно интерпретировать как ответственный за описание линеаризованного гравитационного взаимодействия. Поскольку выражение (3.1) составлено из квадратичных комбинаций токовых характеристик U ab = j ^a ) j ( b ) ^ электромагнитных взаимодействий, то отсюда следует гипотеза, что гравитация в известном смысле не является самостоятельным видом взаимодействия, а индуцируется квадратичными вкладами от электромагнитного прямого межчастичного взаимодействия.

Однако на пути обоснования данного утверждения лежат решения двух вопросов. Во-первых, в формуле (3.2) вместо масс стоят квадраты электрических зарядов и, во-вторых, (3.2) и (3.3) отличаются коэффициентами перед последними слагаемыми в круглых скобках. Эти два фактора играют в развиваемой теории принципиально важные значения. В следующем пункте мы обсудим их в отдельности.

Отметим еще одно обстоятельство. Как известно, гравитационные взаимодействия, описываемые общей теорией относительности, являются нелинейными. В данном реляционном подходе нелинейность гравитационных взаимодействий описывается диагональными минорами третьего и четвертого порядков. Обратим особое внимание на тот факт, что их не бесконечно много, как можно было бы ожидать, исходя из соответствия с общей теорией относительности, а всего два вида: трех- и четырехчастичные.

Можно показать, что линеаризованное гравитационное взаимодействие, описываемое диагональным минором второго ранга (3.1), позволяет описать классические эффекты отклонения света, проходящего вблизи гравитирующего объекта (Солнца или звезд). Описание второго вида классических эффектов общей теории относительности – смещения перигелия Меркурия – достигается учетом диагонального минора третьего ранга [17].

4. Электромагнитный вклад в массу

Поскольку в формуле (3.2) вместо масс стоят квадратичные комбинации электрических зарядов, которые могут принимать лишь положительные значения (как и массы), в отличие от электрических зарядов в минорах первой степени (отвечающих обычным электромагнитным взаимодействиям зарядов различных знаков), то их естественно связать с прообразами масс (гипотетическими вкладами в массу) идеализированных микрочастиц. Эта трактовка подтверждается сравнением формул (3.2) и (3.3).

С другой стороны, при сделанном выводе о связи квадратов зарядов и масс прообраз гравитационного действия при необходимой размерности должен определяться произведением масс и ньютоновой гравитационной постоянной G, откуда имеем mim2  п e ч     VC2e2    ',. (^Х №   гтг

S^va’ ~ g ---- = C 2— ^ m =      = VC2 T- \ 77 = VC2am pi ,       (4.1)

c        ~c2           G~c         ~c    G где mpi ' 10-5 г - планковская масса.

Таким образом, в данном подходе масса идеализированных микрочастиц определяется произведением постоянной тонкой структуры, планковской массы и квадратного корня из безразмерного весового вклада C 2 . Выбором значения весового коэффициента можно добиться любого значения массы идеализированной микрочастицы. Для случая нуклона следует положить C 2 ' 10 - 36 , а для электрона C 2 ' 10 ^-42 . Фактически, весовой коэффициент C 2 играет роль перенормирующего фактора, переводящего значение планковской массы в наблюдаемое значение. В данной модели этим коэффициентом объясняется аналогичная процедура перенормировки планковских масс в унарных многомерных геометрических моделях физических взаимодействий типа теории Калуцы.

Обратим внимание на тот факт, что безразмерные константы C 2 и C ₂ ⁰ имеют значения, близкие (в смысле логарифмических порядков) к корню квадратному из числа Эддингтона 10 80 .

Заметим, что в данной теории возникают две тройки зарядов и масс: безразмерные, размерные элементарные и суммарные значения для макротел.

Так, для случая зарядов это следующие величины:

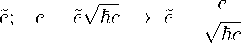
^e ( i⊂a )

(4.2)

(В последнем выражении сумма идет по всем частицам макротела a.) Аналогично для масс имеем безразмерный прообраз, размерное значение массы идеализированного заряда и массу макрообъекта:

m е ² VC = ал/с2; mo = aVC^m pi ; m a = ^ m o (i). (4.3)

( i ⊂ a )

Сумма квадратов, как известно, существенно отличается от квадрата суммы слагаемых, то есть масса макротела всегда положительна и отлична от нуля даже в случае электрически нейтральных тел.

Данные рассуждения касаются некой упрощенной (идеализированной) модели (toy model), которая может претендовать лишь на вскрытие закономерностей качественного характера. В рамках этой модели все элементарные частицы имеют одинаковые массы, жестко связанные со значением элементарного электрического заряда (электрона). Это допустимо для описания классической теории, где несущественны детальные свойства составляющих их микрочастей, однако для построения реалистической теории элементарных частиц необходимо обобщить теорию на случай, во-первых, комплексных отношений и, во-вторых, на случай бинарных систем отношений, что выходит за рамки данной статьи.

• 5.    Природа “свободного” действия в реляционном подходе

Из сравнение формулы (3.2) с фоккеровским действием для линеаризованной гравитации (3.3) видно, что они отличаются коэффициентом 2 при последних слагаемых в круглых скобках. С другой стороны, при получении формулы (3.2) ничего не говорилось о так называемом “свободном” действии макрочастицы, которое присутствует в фоккеровском действии Грановского– Пантюшина (3.3). Это позволяет предположить, что “свободное” действие макрочастицы обусловлено именно различием коэффициентов в сравниваемых формулах.

Другой довод в пользу данного предположения состоит в том, что в реляционном подходе бессмысленно понятие “свободной” частицы. Частицы могут рассматриваться лишь в отношениях с другими частицами. То, что в общепринятых формулах трактуется вкладом в действие “свободной” частицы, должно получаться из отношений рассматриваемой частицы с частицами окружающего мира.

Оставляя в (3.2) лишь слагаемые без скоростей с коэффициентом 1, можно записать

^{S fre} e ^(a)=  cm a jds a =

----a ^^ mb / I 5(s²(a, b))ds _a ds b . c b 6= a

(5.1)

Следующее рассуждение носит постулативно-эвристический характер, но представляется концептуально полезным и позволяющим получить интересные следствия. Учитывая, что в определение дельта-функции, согласно (1.2), неявно входит расстояние между выделенной и другой частицей, приведенное выражение (5.1) после суммирования (усреднения) по всем частицам можно трактовать как отношение полной массы материи во Вселенной M к некоторому среднему расстоянию порядка линейных размеров наблюдаемой Вселенной R g . Существует представление о том, что эти величины могут быть связаны как масса и гравитационный радиус массивного источника в ОТО, в силу чего приходим к постулату о суммировании:

X mb [ 5(s2(a,b))dsb 2M ' c^. (5.2) Rg G b=a y

Получившееся соотношение означает в реляционном подходе обусловленность лагранжиана “свободных” частиц их взаимодействием со всеми частицами окружающего мира (Вселенной) в духе принципа Маха.

• 6.    Обобщение прямого электромагнитного взаимодействия

Рассмотрим другой тип миноров второго ранга из закона (2.2), который уголком затрагивает диагональ. Этот минор уже описывает трехчастичные взаимодействия. Покажем, что данный минор является ответственным за явления двух типов. Во-первых, он описывает гравитационное влияние на электромагнитные взаимодействия двух частиц со стороны третьих частиц, а, во-вторых, он приводит к дополнительным (перенормирующим) вкладам в значения электрических зарядов взаимодействующих частиц.

Начнем с рассмотрения первого типа явлений.

Пусть по-прежнему выделены частицы с номерами a и b. Минор, описывающий взаимодействие с участием третьей (диагональной) частицы с индексом c, можно представить в следующих видах:

D(b = ab,c

u ab u ac

U cb    e 2

U ba u ca

u bc

2 ² e _c

= ё а ё ь ё ² (U ab - U ac U cb ) =

e _a e _b e _{c µ ν                                    α β}

(6.1)

2    ^U ( a ) ^U ( b ) ⁽²ⁿ ^v ^п ав    ⁿ ^a ⁿ ve    ^п ^в ⁿ va ^)u ( c ) ^U ( c ) ^.

Перейдем, как и прежде, от идеализированных микрочастиц a, b, c к составным частицам или телам (обозначим их также a, b, c), произведя суммирование выражен ия (6.1) по составляющим их микрочастицам. Кроме того, учтем ранее введенный коэффициент VC и перейдем в ходе суммирования к размерным величинам на основе соотношений (4.2) и (4.3):

, ■,. _ч q a q b m c ,       q a q b Gm c

~VC2Ipieaebmc ^lpi =5-, c mpi где, напомним, lpi = VG~/c3 - планковская длина, a mpi = xjc~/G - планковская масса.

После этих процедур из выражения (6.1), умноженного на ~ , напишем прообраз (подынтегрального выражения) действия в размерных единицах:

5(e,g) _ qaqb _,ц „,v                                    ^.a „,в Gmc R(3)

S(ab,c) = c U(a)U(b)V2n^vПав n^aHve n^enva)u(c)u(c) 2c2 Babc.(

Здесь введен координатный трехточечный вклад В а 3,) _с , структура которого воспроизводится из более ранних работ [15]: B ab ⁾ c ~ B ab ) (в О²) + B b ²).

Представим полученное выражение в виде суммы двух слагаемых:

c ^{( e},^{g )} _ q ^a q ^b „.^g V (         _         _         '. a ^e Gmc o⁽³⁾ 1

^S ( ab,c ) = c ^U ( a ) ^U ( b ) V^{n gV П ав n} ^^{a n ve n} ^^{e n va )u} ( c ) ^u ( c ) 2c 2 ^B ab,c +

+ q a q b ⁽u (a ) n ^gv ^U Vb ) ⁾⁽u ac ) n ae u ^ ) ) Gm B Obc .                         ⁽6.⁴⁾

Интерпретация слагаемых в первой и во второй строках различна и напоминает проделанное в предыдущей главе обоснование “свободного” слагаемого в действии, однако последнее в данном случае имеет иной характер.

Сравнивая первую строку (6.4) с выражением прямого линеаризованного гравитационного взаимодействия (3.3), находим, что данный прообраз действия включает в себя тензорный гравитационный потенциал ^ ^_v (с), создаваемый третьим телом (частицей) с. Собирая вместе прообразы действия прямого парного электромагнитного взаимодействия (1.1) и тройного взаимодействия из первой строки (6.4), приходим к выражению:

c ( e ) I Q ^{( e,g)} __ S ( ab ) ⁺ S ( ab,c ) =

q a qb ^g „v o(2) c u ( a ) u ( b ) B ab ^X

^X (n^v - "^CT ⁽n ^v П ав - n ^a n ve ^- П дв n va ^)u ac ) u ^ec ) ^{(B {}ae ⁺ B^)

(6.5)

которое следует трактовать как прообраз действия прямого межчастичного электромагнитного взаимодействия двух (макро)частиц a и b, испытывающих гравитационное воздействие со стороны третьей массивной (макро)частицы c. В стандартной теории поля это соответствует электромагнитным взаимодействиям двух частиц в гравитационном поле, создаваемом третьим массивным телом. Это, например, может быть электромагнитным взаимодействием частиц в гравитационном поле Земли.

Учитывая выражения координатных вкладов в двух- и трехчастичные взаимодействия, в символическом виде эффективная метрика в первом приближении по G записывается в форме:

g ^v ^(a, ^b)   >  n ^v

Gm c

/ ds c I 2c 2 ^{(n g}v ^п ав

η µα η νβ

B ⁽³⁾ \ β B ab,c

П мв n-u.X.    2    .

B _ab

(6.6)

• 7.    Перенормирующие вклады в электрический заряд

Обратимся к выражению, записанному во второй строке (6.4):

q^aq^b      _n ,,v А/ а ^в A Gmc „(З)

c ⁽u ( a ) ⁿ ^^{v U} ( b ) ^)(U ( c ) ^{n ae} u ( c ) ) 2c 2 B ab,c ^{.                                  (7Л)}

Это выражение следует трактовать как дополнительный вклад в электромагнитное взаимодействие (макро)частиц a и b от частиц c окружающего мира.

Вклад в действие взаимодействия получается интегрированием по мировым линиям частиц:

да⁽ e,g) _        a a q ^^r.,^           _x G X m B abc

^S ab             ds a ds b c ^(и ( а ) ^и ц ( Ь ) ^)B ab ^X    . 2 / ,    ds c m c   ,₂. .                (⁷.2)

^{J J}                                    e=^b^J         B ab

Суммирование по всем массам окружающего мира приводит, во-первых, к вкладу от фоккеров-ского электромагнитного взаимодействия, и во-вторых, к некоторому добавку, обусловленному тем, что суммирование производится за вычетом частиц a и b. Тождественно добавляя и вычитая отвечающие им слагаемые, после преобразований подынтегрального выражения с учетом постулата о суммировании (5.2) получим:

µ

Л c(e,g)     [ [ j j   ^U(a)^Ug(.^b) _d(2)           ₁      ^mb ,      / \ ^ma ,      /,\

(7.3)

(7.4)

^ ^Sab ==      ds a ds b -------- B_ab X q a q b 1 -  ---I pi C b (a) -  ----I pi C a (b)

J J            c                L    2mpi           2mpi где использовано обозначение для коэффициента

Cb(a) = [ dsb5(slb) ^ —, rab по порядку величины определяемого средним расстоянием rab между частицами.

Тогда с точностью до ничтожно малых слагаемых, определяемых членами порядка ^ O[( mm a r Pl ) ² ], полученное выражение можно представить в фоккеро-подобном виде с перенормированными на малую поправку зарядами взаимодействующих частиц:

AS aeb^{,g )} ' / ds a ds b q a cq b (u ^a ) U M ( b ) )B a ² b ⁾ ,

(7.5)

где эффективные заряды частиц содержат добавку Aq, пропорциональную их массам:

q a = q a

1 - Jm l pi C a (b) 2m pi

q b = q b

1 - z-b- l pi C b (a) 2m pi

(7.6)

Зависимость перенормирующего коэффициента от массы означает необычную гипотетическую возможность малой зарядовой асимметрии у различающихся по массе частиц (например, электрона и протона), что могло бы критическим образом сказаться на определенных квантовополевых представлениях о характере электромагнитных взаимодействий. Вместе с тем, наличие планков-ских множителей делает данные перенормирующие коэффициенты, по-видимому, лежащими за пределами экспериментальной точности. Вполне вероятно также, что данный эффект может быть нивелирован учетом других миноров (в частности, 4-частичного сектора взаимодействий).

Однако если пытаться искать условия, при которых данный эффект все же мог бы давать вклад, следовало бы обратиться к случаю больших масс (астрофизические объекты), для которых главные значения электрических зарядов скомпенсированы, а пропорциональный массам добавочный член мог бы оказаться существенным. В частности, он мог бы дать вклад в картину формирования магнитного поля планет, обусловленного их вращением. Идея генерации поля вследствие разделения объемных и поверхностных зарядов в сочетании с эффектом вращения небесных тел высказывалась достаточно давно различными авторами, в частности, Сазерлендом [18].

Полученный результат вкупе с возможными астрофизическими проявлениями перекливается с результатом, полученным ранее на базе 6-мерной геометрической модели типа Калуцы—Клейна [19] с двумя абелевыми векторными полями. Было показано, что при определенном способе размерной редукции на 4-мерие у заряженных частиц индуцируется дополнительный заряд согласно формуле Aq ~ ^√ Gm.

Заключение

Исходя из изложенного, можно сделать следующие выводы:

• 1.    Рассмотренные здесь простые прямые электромагнитные и линеаризованные гравитационные взаимодействия можно трактовать как усеченные следствия более общих (многочастичных) взаимодействий, содержащих в себе вклад частиц окружающей Вселенной в соответствии с принципом Маха.

• 2.    Учет миноров, отвечающих трехчастичным взаимодействиям, удовлетворяет принципу соответствия с результатами стандартных теорий. В частности, это относится к описанию электромагнитных взаимодействий в искривленном пространстве-времени, а также к описанию классических эффектов общей теории относительности, обязанных нелинейности гравитации.

• 3.    Реляционный подход к описанию пространства-времени и взаимодействий приводит к концептуальному расширению современных представлений о соотношении электромагнетизма и гравитации, а также к ряду характерных следствий, некоторые из которых могут быть косвенно наблюдаемыми (в частности, возможные проявления слабой зарядовой асимметрии в возникновении магнитных полей у астрофизических объектов).