К теории уравнения Бельтрами переменного типа со многими складками

1. Уравнение Бельтрами переменного типа: уточнение понятий

Пусть в односвязной области D С C задано дифференциальное уравнение

A(z)/ _Z (z) + В (z^fe(z) = 0, (z = х + гх 2 G D),

где A(z), B(z) ( | A(z) | = | B(z) | почти всюду в D ) — конечные измеримые комплекснозначные функции. В случае А = ц, В = — 1 уравнением (1) является уравнение Бельтрами (см. [2, гл. 2]),

^f z ^{( z} ) = V^{( z} ) ^f z ^{( z} ),

имеющее при условии

esssupp’ |ц(г)| < 1 во всякой подобласти D' b D гомеоморфное решение w = /(z), принадлежащее классу WlOc вместе с обратным. Это решение единственно с точностью до суперпозиции с конформным отображением.

В дальнейшем решением уравнения (1) будем называть непрерывную функцию /(z) G W lO ’ _c2 (D) , удовлетворяющую ему почти всюду в D .

Напомним [1, c. 7], что коэффициент p(z) = Д (z )// _г (z) называется комплексной дилатацией отображения / (z) Е W lO^ D) . Его задание эквивалентно заданию почти всюду в D поля распределения характеристик Лаврентьева (p(z),6(z)) (см. [3]). Отображение w = / (z) , первая характеристика которого почти всюду в D удовлетворяет условию

p(z ) < Q = const, (3)

называется Q - квазиконформным . Если условие (3) выполняется в D локально (то есть со своим Q = Q(D ’ ) для всякой области D' b D ), то отображение называется локально квазиконформным . Условие ess sup _D | ^(z) | < 1 ( esssup _D ‘ | ^(z) | < 1 для всякой области D ‘ b D) эквивалентно условию квазиконформности (локальной квазиконформности).

Уравнение Бельтрами с | ^(z) | < 1 почти всюду в D будем в дальнейшем называть классическим . Случаи | ^(z) | < 1 почти всюду в D и | ^(z) | > 1 почти всюду в D отличаются тем, что в первом случае гомеоморфные отображения не меняют ориентацию, а во втором меняют. Различие здесь лишь формальное. Интерес представляет ситуация, когда одновременно существуют подобласти D , в которых почти всюду выполнено | ^(z) | < 1 и подобласти D , в которых почти всюду | ^(z) | > 1 . В этом случае говорится, что уравнение Бельтрами имеет переменный тип. Его решения описывают отображения со складками, сборками и т. п. Задача исследования таких уравнений была поставлена Л.И. Волковыским [3], а ряд успехов в этом направлении был сделан в работах Э.Х. Якубова и У. Сребро [16–18]. Следует отметить, что уравнение (1) впервые рассматривалось в работе [16]. В той же работе [16] было изучено строение отображений со сменой ориентации в окрестности критических точек (то есть точек, в любой окрестности которых отображение негомеоморфно), лежащих на линии смены типа. В частности, в этой работе было дано описание некоторых важных случаев таких точек — точек, в которых отображение является складкой, зонтиком или (p, q) -сборкой.

В настоящей работе изучаются общие закономерности в строении отображений, описываемых уравнением (1), смена типа которого происходит во многих подобластях области D .

Пусть существует замкнутое относительно D множество Е С D меры mes ₂ Е = 0 . Если непрерывная в D функция /(z) является решением уравнения (1) в D \ Е , при этом принадлежность / Е W lO ’ _c ² (D) не известна, то функцию /(z) будем называть решением с особенностью Е данного уравнения.

Наличие особенностей у решений характерно для уравнений (1), вырождающихся на некотором множестве Е, то есть таком Е, что eesVSfJ^)| - |В(z)|1 = 0

“г (s) D для всякого г > 0, где ВТ (z) — круг с центром z Е Е. При этом в качестве Е часто выступает множество смены типа уравнения (1), то есть множество раздела между {z : z Е D, |Л(^| < |В(z)|} и {z : z Е D, |Л(^| > |В(z)|}.

Пусть D С C — область. Пусть задано конечное семейство жордановых дуг Г = {?}, разбивающих D на конечный набор подобластей Т(Г) = {Dj}^=1. Дуги, входящие в семейство Г, могут быть открытыми, замкнутыми или полуоткрытыми, то есть взаимно-однозначными образами интервала, отрезка или полуинтервала. Мы будем различать понятия замкнутой жордановой дуги и жордановой кривой. В первом случае будет иметься в виду дуга, включающая оба конца, а во втором — непрерывный взаимно-однозначный образ окружности S 1, или, другими словами, замкнутая дуга, у которой начало и конец совпадают.

Определение 1. Пусть имеется полуоткрытая дуга у , заданная непрерывным взаимнооднозначным отображением z = z(t) : [a, b) ^ C . У нее определен конец при t = a — точка z(a) , но не определен конец при t = b . В этом случае под концом понимается точка z ₀ Е C , определяемая равенством

Z 0

= lim z(t), t ^ b - 0

если такая точка существует. Точку z(a) будем при этом называть собственным концом дуги у , а точку z ₀ — несобственным.

Аналогично определяются понятия несобственного конца полуоткрытой дуги у вида z = z (t) : (a, b] ^ C при t = а , а также несобственных концов открытой дуги z = z (t) : (a, b) ^ C при t = a и t = b , если они существуют. Замкнутая дуга z = z (t) : [a, b] ^ C имеет два собственных конца z (a) и z(b) .

В дальнейшем договоримся обозначать через ( a, b ) любой промежуток вида (a,b) , (a, b] , [a, b) или [a, b] . Положим

Я г = U [у ]•

7GF где [у] = {z : z = z(t), t Е (a, b)} обозначает носитель дуги у.

Относительно дуг семейства Г предполагаем следующее.

• 1)    Всякая дуга из семейства Г имеет ровно два конца, собственных или несобственных.

• 2)    Разные дуги могут иметь общими разве лишь концевые точки.

• 3)    Все конечные несобственные концы лежат на границе области dD . Какая-либо точка области D может быть разве лишь собственным концом некоторого четного набора дуг, в количестве не менее 4-х (или, что то же самое, быть общей граничной точкой не менее 4 областей D j ).

• 4)    Среди замкнутых дуг у Е Г нет вырождающихся в точку.

• 5)    Каждая дуга без концевых точек является частью границы двух и только двух областей { D j } .

В дальнейшем, говоря о концах рассматриваемых дуг, слова «собственный» и «несобственный» мы будем опускать, считая ясным из контекста, о концах какого вида идет речь.

Определение 2. Разбиение Т (Г) = { D _j } j =₁ называется правильным, если оно допускает черно-белую раскраску, то есть такую раскраску, что любые две области D _t и D j , имеющие общую невырожденную граничную дугу у Е Г , имели разные цвета (см. рис. 1).

Очевидно, что в случае правильности разбиения Т (Г) раскраска однозначно определяется указанием цвета любой из областей и существует только две возможные раскраски. В частности, можно считать, что раскраска Т (Г) определяется приписыванием области D 1 белого цвета.

В дальнейшем речь будет исключительно о черно-белых раскрасках, поэтому слова «черно-белая» будут опускаться.

Кроме того, договоримся считать, что всякий гомеоморфизм / : D ^ /(D) индуцирует в /(D) разбиение Т (/ * Г) = { / (D i )} . При этом раскраска Т (/ * Г) сохраняется, если / сохраняет ориентацию, и меняется на другую, если ориентация меняется.

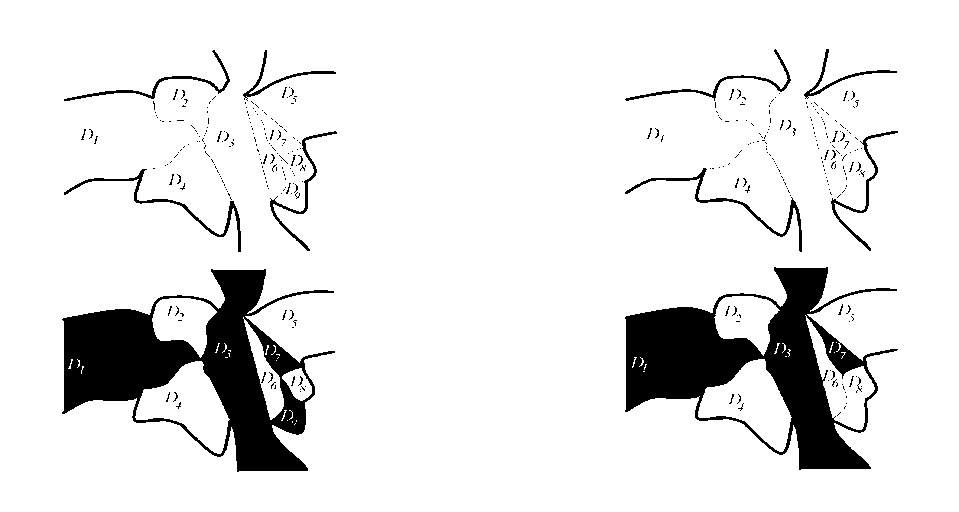
Правильное разбиение области D

Неправильное разбиение области D

Рис. 1. Виды разбиений

Напомним [8, гл. 2, § 3, п. 35], что дуга 7 С C, заданная в виде г = /(t) : (а, 3) ^ C, /‘(t) = 0, где /(t) — аналитическая по вещественному переменному t функция, называется аналитической.

Определение 3. Пусть в области D с разбиением Т (Г) с заданной раскраской определено уравнение (1), причем | А(г) | < | В(г) | п.в. в белых областях D _t и | А(г) | > | В(г) | п.в. в черных областях D _t . Предположим, что /(г) : D ^ C решение с особенностью Е _г этого уравнения и для него выполнены свойства:

• 1)    отображение / гомеоморфно в каждой из подобластей D _t и на каждой дуге 7 ^ Г ;

• 2)    отображение / сохраняет ориентацию в каждой белой области и меняет в каждой черной области.

Тогда будем называть отображение / (А, В ) -мультискладкой.

В случае когда отображение / является (А, В ) -мультискладкой, критическими точками являются точки всех дуг, входящих в семейство Г . В терминах степени отображения (см., например, [7]) (А, В ) -мультискладки / можно охарактеризовать тем, что локальная степень отображения в этих точках равна deg(/, г) = 0 . В белых областях deg(/, г) = 1 , а в черных deg(/,г) = - 1 .

Гомеоморфное отображение области D С C , осуществляемое голоморфной функцией, будем называть, следуя [9, с. 92], конформным отображением первого рода , а осуществляемое антиголоморфной функцией будем называть конформным отображением второго рода . Отметим, что голоморфность или антиголоморфность гомеоморфности не подразумевает.

Следуя работе [6], уравнению (1) будем ставить в соответствие классическое урав- нение Бельтрами с комплексной дилатацией

' -A(z)/b(z) при |a(z)| < |b(z)|,

/ * ^(г) = <

-B(z)/A(z)

при ^{| a(z) |} >  ^{| B (z} ) | .

Это уравнение называем в дальнейшем уравнением, ассоциированным с уравнением (1).

Отметим, что для уравнения Бельтрами (2)

/ * ^(г) = <

/(г)

^1/ / ^(z )

при Нг) < 1, при Нг)| > 1,

• и, значит, в классическом случае /(г ) = / * (г) .

Замечание. Связь между уравнениями Бельтрами переменного типа и ассоциированными уравнениями Бельтрами впервые отмечена в [12], а сам термин был введен нами в [6]. В этих работах показано, что складчатые решения уравнения Бельтрами переменного типа получаются из решений ассоциированного с ним уравнения с помощью дополнительной суперпозиции с функцией Бора B ( z ) = х-1 + г | ж ₂ | . В следующей теореме показывается аналогичная связь в случае, когда уравнение имеет несколько областей, в соседних из которых уравнение имеет разный тип.

Теорема 1. Предположим, что в области D с правильным разбиением Т(Г) и заданной черно-белой раскраской задана (A, B) -мультискладка /(г) : D ^ C . Предположим также, что существует w = / 0 (г) : D ^ / 0 (D) — гомеоморфное решение с особенностью Е _Г , уравнения ассоциированного с (1) . Кроме того, предположим, что для всякого г выполнено / 0¹ G W _lOc2 (/ ₀ (D _i )) и / - G W lO ’ c² (/(D _i )) , где / - ¹ ветвь многозначной функции / ^{- 1} , соответствующая D _i .

Тогда:

• 1)    /(/ с Т ¹ (w)) конформное отображение первого рода всякой белой области / 0 (D _i ) и конформное отображение второго рода всякой черной области / 0 (D _i ) ;

• 2)    дуги / 0 (7) без концевых точек — аналитические.

Доказательство. Будем обозначать £ = /(г). Пусть D _i — некоторая белая область. Тогда отображения / и / 0 имеют в D _i одну и ту же комплексную дилатацию /(г) . Отображение /(/ ^{— 1} (w)) : / 0 (D _i ) ^ /(D _i ) почти всюду переводит бесконечно малые круги области / 0 (D _i ) в бесконечно малые круги области /(D _i ) . Как суперпозиция отображений класса W lOc отображение / (/0¹(w)) есть отображение класса WiOC (см., например, [14, лемма 6.4, с. 151]). В силу стандартной аргументации (см., например, [10, доказательство теоремы 1]) заключаем о его конформности первого рода.

Пусть теперь D _i — некоторая черная область. Тогда легко видеть, что отображения g(г) = /(г) и / 0 (г) имеют в D _i одну и ту же комплексную дилатацию /(г) . Отсюда заключаем, что отображение g(/₍ ^{- 1} (w)) : / 0 (D _i ) ^ g(D _i ) почти всюду переводит бесконечно малые круги области / 0 (D _i ) в бесконечно малые круги области g(D _i ) .

Как и выше, отображение g(/ — ¹ (w)) как суперпозиция отображений класса W lO ’ c² есть отображение класса W lO ’ c . Отсюда заключаем о конформности второго рода отображения g^{( /} o¹⁽w)') = У ^И).

Докажем теперь аналитичность всякой дуги / 0 (7) , если 7 некоторая общая смежная граничная дуга двух областей D ^ и D j .

Пусть для определенности D _j — белая область, а D j — черная.

Заметим, что 7 * = /(7) — жорданова дуга, как гомеоморфный образ жордановой дуги. Рассмотрим область D * = /(D _j ) U / (D j ) .

Отображение C = / (z) сохраняет ориентацию в D j и меняет ее на противоположную в D j . Поэтому области /(D _j ) и / (D j ) имеют непустое пересечение, примыкающее к 7 * .

Если область D * односвязна, то отобразим ее конформно в нижнюю полуплоскость комплексной плоскости так, чтобы образ множества 7 * лежал на вещественной оси. Пусть тогда C i = ^(C) — данное отображение.

Если область D * неодносвязна, то возможны две ситуации:

( * ) 7 * = /(7) лежит на внешней компоненте связности границы 9D* , ( ** ) 7 * = /(7) лежит на некоторой внутренней компоненте связности границы dD * .

В случае ( * ) пусть C 1 = V 1 (C) конформное отображение области D — минимальной односвязной области, содержащей D * , в нижнюю полуплоскость комплексной плоскости, переводящее дугу 7 * в промежуток на вещественной оси.

В случае ( ** ) пусть C 2 = ^ 2 (C) конформное отображение области D * на некоторую область D ** , такое, что граничная компонента dD * , содержащая 7 * , перейдет во внешнюю компоненту границы dD ** . Пусть D — минимальная односвязная область, содержащая D ** и C 1 = ^ 3 (C 2 ) — конформное отображение D в нижнюю полуплоскость комплексной плоскости, переводящее дугу ^ 3 (7 * ) в промежуток на вещественной оси. Положим ^ 1 = ^ 3 о ^ 2 .

Отметим, что в силу принципа соответствия границ для конформных отображений, отображение ^1 : D* ^ ^1(D*) продолжается на D* ^7* по непрерывности взаимно однозначно. Положим v = Ф(z) = <

^ i ^(/(z))

^ i ^(/(z))

при z G Dj|j7, при z G D j .

Из процесса построения отображения Ф ясно, что оно гомеоморфно в D _j [J D j [J 7 , причем Ф, Ф ^{- 1} G И ^¹/ , ² в областях D _s и Ф(D _S ) (s = г,/) соответственно и в D _j и D j его комплексная дилатация совпадает с комплексной дилатацией / 0 (z) .

Рассмотрим отображение

Ф^) = / о (Ф ^{- 1} (v)) : Ф(D) ^ / o (D).

Из доказанного выше следует конформность Ф(v) в областях Ф(D _j ) и Ф(D j ) .

Поскольку прямая Im v = 0 локально спрямляема, то, по теореме Пенлеве [11, гл. 2, § 26], заключаем о конформности Ф(v) во всей области Ф(D) .

Аналитичность дуги / 0 (7) следует из равенства / 0 (7) = Ф(Ф(7)) , того факта, что Ф(7) есть промежуток на прямой Im v = 0 ив силу неравенства Ф/ v) = 0 , справедливого внутри области Ф(D) . Теорема доказана.

• 2.    Конформные мультискладки

Определение 4. Отображение ио = f (z) : D ^ C называется конформной мультискладкой с правильным разбиением Т (Г) = { D _i } области D и заданной черно-белой раскраской, если: 1) дуги, составляющие семейство Г , — аналитичны, за исключением, быть может, концов; 2) в каждой белой области D i отображение является о = f (z) конформным первого рода, а в каждой черной области D i отображение является о = f (z) конформным второго рода.

Следствие теоремы 1. При выполнении условий теоремы 1 (А, В' ) -мультискладка f (z) представима в виде

f(z) = V(fo(z)), где у — конформная мультискладка в f0(D) с разбиением Т(foГ).

Таким образом, из всего полученного выше можно заключить, что задача описания (А, В) -мультискладок сводится к задаче описания конформных мультискладок. В общем случае эта задача представляется достаточно сложной, однако можно отметить следующее свойство единственности, характеризующее всю совокупность конформных мультискладок с заданным разбиением с раскраской Т (Г) .

Теорема 2. Пусть о = f1(z) и £ = f2(z) — конформные мультискладки области D с одним и тем же разбиением Т(Г) = {Di} с заданной раскраской. Тогда существует аналитическая функция у : f1 (D) ^ f2(D), такая, что f2(z) = V(fi(4Y

Доказательство. Пусть D _i и D j — произвольные соседние области с общей граничной дугой 7 G Г и для определенности D _i — белая область, а D j — черная область.

Тогда f ₁ (D _i ) и f 1 (D j ) — две области, примыкающие к дуге f 1 (7) , а f ₂ (D _i ) и f ₂ (D j ) — две области, примыкающие к дуге f ₂ (7) . Причем в обоих случаях примыкание происходит «с одной» стороны.

Рассмотрим в f ₁ (D _i ) и f 1 (D j ) конформные отображения

^F i ^{( w )} = ^f 2 i ^{(f -} 1И ), F j ^{( о )} = ^f 2 j и-Ч ⁰ ))

где г, з указывают, что берутся ветви f 1 и f ₂ , соответствующие D _i и D j .

Пусть А ^. — компонента связности f ₁ (D _i )Q f ₁ (D j ) , примыкающая к дуге f 1 (7 ) . Поскольку, очевидно, F^w) = F j (о) на f 1 (7) , то из теоремы 1 [5, с. 99] легко следует, что F _i (w) = F j (о) в А ^ . Тем самым F _i (w) и F j (о) являются аналитическими продолжениями одного и того же аналитического элемента (F _i (w), А ^ ) = (F j (w), А^-) .

Ясно, что тогда и любые две функции (необязательно порожденные соседними областями D _i и D j )

^F i ^(w) = ^f 2 i ^{(f -} 1 ^(о)), ^F j ^{( w )} = ^f 2 j ^{(f - 1 (w))}

являются аналитическими продолжениями друг друга. В целом они образуют некоторую аналитическую функцию y(w) . Теорема доказана ² .