К вопросу анализа ограничений на значения параметров в пространстве действий автономных интеллектуальных систем

DOI:

В данной работе рассматривается такой класс автономных интеллектуальных систем (АИС), как беспилотные летательные аппараты (БПЛА) [1-3]. В настоящее время БПЛА активно используются для решения различных задач, в том числе, в рамках реализации транспортно-технологических циклов БПЛА [4-6]. Часто такие задачи носят межотраслевой характер.

При управлении беспилотным летательным аппаратом, как элементом АИС, возникают проблемы его взаимодействия с другими БПЛА, а также со статическими и динамическими объектами внешней среды. Особенностью является автономный режим управления и функционирования в пространстве действий АИС. Анализ ограничений на значения параметров в пространстве действий автономных интеллектуальных систем актуален для роевого применения БПЛА, в частности, в точном земледелии, для защиты растений с использованием БПЛА-распылителей, а также для контроля обширных площадей сельскохозяйственных культур [7, 8].

В статье [9] отмечается, что в последнее время усиливается значение практического применения АИС, таких как рои дронов. Авторы отмечают, что это обусловлено появлением множества устройств, способных коммуницировать между собой с целью их кооперативного поведения. Управления роем дронов является сложной задачей из-за наличия постоянно изменяющихся условий окружающей среды и ограничений каналов беспроводной связи, используемых каждым беспилотным летательным аппаратом в пространстве действий.

При оперировании в пространстве действий АИС регистрирует входную информацию, это могут быть какие-либо входные параметры. Причем в зависимости от значений этих входных параметров может возникать сообщение о недопустимости или приближении к некоторому «пограничному» значению параметра. Другими словами, система регистрирует недопустимое соотношение значений входных параметров, т.е. фиксирует некоторые ограничения.

ОГРАНИЧЕНИЯ НА ЗНАЧЕНИЯ ПАРАМЕТРОВ АИС

При функционировании автономных систем в реальных условиях на параметры накладываются ограничения. Наиболее просто ограничения описываются крайними значениями параметров, которые они могут принять. Но в большинстве случаев, знания только крайних значений параметров недостаточно, могут быть промежуточные ограничения значений параметров или более сложные случаи ограничения значений параметров.

Пример, представленный на рисунке 1, дает представления о двух интервалах значений, то есть, когда ограничения на параметры описываются следующим образом: vol pa, = [ 0...1 ] n ( 10...100 ) .

В примере один параметр имеет интервалы значений, а контур из совокупности двух параметров описан некоторой функцией от X , Y .

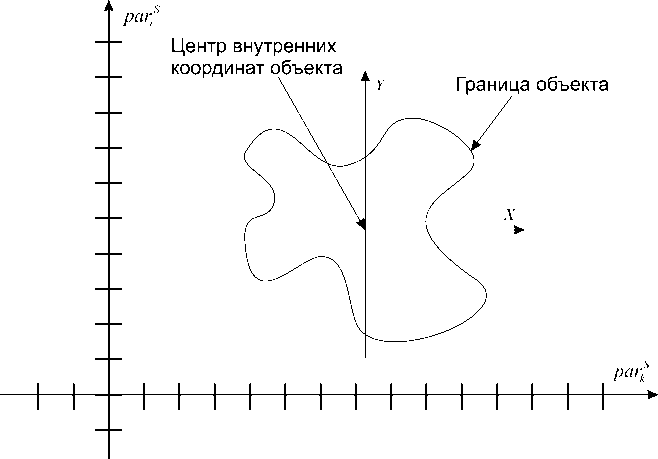
Рисунок 1. Граница объекта в двухмерном пространстве.

• Figure 1.    Object boundary in 2D space.

Точки внутри границы объекта не должны достигаться другими объектами. То есть, значение координаты какой-либо точки, какого-либо объекта не должно быть внутри указанной границы. Зная все значения параметров X и Y для которых известно, что они лежат внутри границы, можно построить матрицу значений X и Y , для которых не может быть значение координат любой точки другого объекта внутри границы, т.е. тех значений координат, которые лежат внутри границы.

Обобщая такие представления об ограничениях, представим ограничения в виде штрафа f ( par ) = 0,1 . Штраф равен единице, если параметры приняли недопустимое значение, и нулю, если параметры приняли допустимое значение. Исходя из этого, строится матрица зависимости значения штрафа от значений параметров par^S и par^S .

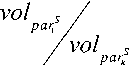
VO1 Par5

fine

V

volⁿ S par_i

	^
vol 1 S parkS	•■ voln s par
1,1 f fin e	f 1 m ffine
f n ,1 f fin e	r n , m f fine v

Во время работы АИС при принятии решения о следующем действии команды автономных систем необходимо провести анализ решений, в ходе которого может происходить обсуждение и «голосование» за выбор оптимального решения. Для обеспечения этого процесса, необходимо чтобы ограничения значений параметров были адаптированы для такого принятия решения и имели унифицированный вид.

Предлагается использовать подход [10], основанный на методах штрафных функций f^ ( par ) = f ⁽ vol_par ) .

Таким образом, получаем для каждого параметра функцию ограничения значений этого параметра. Так как в большом количестве случаев штрафная функция является достаточно сложной структурой, то для организации хранения информации в автономной системе целесообразно использовать матрицу зависимости значения штрафа от значения параметра, или набора параметров, если такая зависимость имеет место и важна.

Текущие значения параметров между зарегистрированными значениями в матрице зависимости учитываются с использованием аппроксимации, вид аппроксимации также зависит от характера ограничения.

Итак, введем ограничения значения параметра в виде функции штрафа. Для определенных значений параметра установлены значения штрафа. Для недопустимых значений параметров сумма штрафа не меньше некоторой пороговой величины, превышать которую при работе АИС нельзя. Для обобщения всех видов функций штрафа сведем такую зависимость ограничений значений параметра к матрице зависимости величины штрафа от значения параметра

Таким образом, ограничения заданы штрафными функциями и определены в виде матрицы зависимости штрафа от значения параметра ffme (Par)

V f fine

f ¹

f fin e f fin e

n

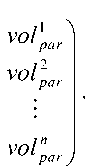
vol par v ^0lP ar

vol n par у

В итоге все зависимости (и зависимость значений, и зависимость штрафа) каждого параметра представлены в виде матриц.

Пороговое значение всех штрафов приведем к нормальному виду, когда значение штрафа, равное единице, является пороговым.

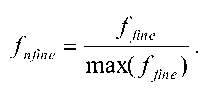
max( f^ )

fin e

При этом значение штрафа не может превышать единицу 0 <  f_nfinPpar ) <  1.

Например, скорость объекта не может превышать какого-либо порогового значения, иначе может произойти разрушение этого объекта. Однако значение штрафа, равное единице в принципе может и не существовать, так как, например, та же скорость объекта может увеличиваться до бесконечности, но чем она больше, тем больше должен быть штраф. Таким образом, получаем бесконечное приближение значения штрафа к единице. При решении задач и при оценке штрафов по совокупности параметров происходит оценка общего штрафа решения. В таблице 1 приведен пример распределения значения штрафа в зависимости от значения параметра.

Таблица 1. Пример распределения значения штрафа в зависимости от значения параметра.

Table 1. An example of the distribution of the penalty value depending on the parameter value.

volpar	0	1	2	3	4	5	6	7	8	9	10	11	12	11
Л fin e	0	0,1	0,11	0,12	0,14	0,16	0,26	0,30	0,41	0,78	0,88	0,98	0,99	1

ПРИМЕР ОБОБЩЕНИЯ ИНФОРМАЦИИ ОБ ОГРАНИЧЕНИЯХ

Для своей собственной оболочки АИС эту информацию может получить опытным путем, например, при приближении другого объекта или предмета, любая его точка не может попасть внутрь некоторого радиуса, либо другого параметра – представляющего границу объекта (см. рисунок 1). Тогда при попытке внедрить предмет внутрь, происходит срабатывание защиты – выдача результата о невозможности достижения значений параметров, то есть координат любой точки объекта таких, когда они находятся внутри объекта. Зная значения параметров, АИС проводит обобщение информации и использует эти знания, заранее определяя возможные значения как своих параметров, так и параметров объекта.

При дальнейшем функционировании, проведя обобщение, система знает заранее, какие действия могут привести к срабатыванию защиты, и для таких действий уже имеется «готовое» значение штрафа. Механизм обработки и хранения такой информации описан ниже. На рисунке 2 приведен пример распределения значения штрафа в зависимости от значения параметра «угол наклона».

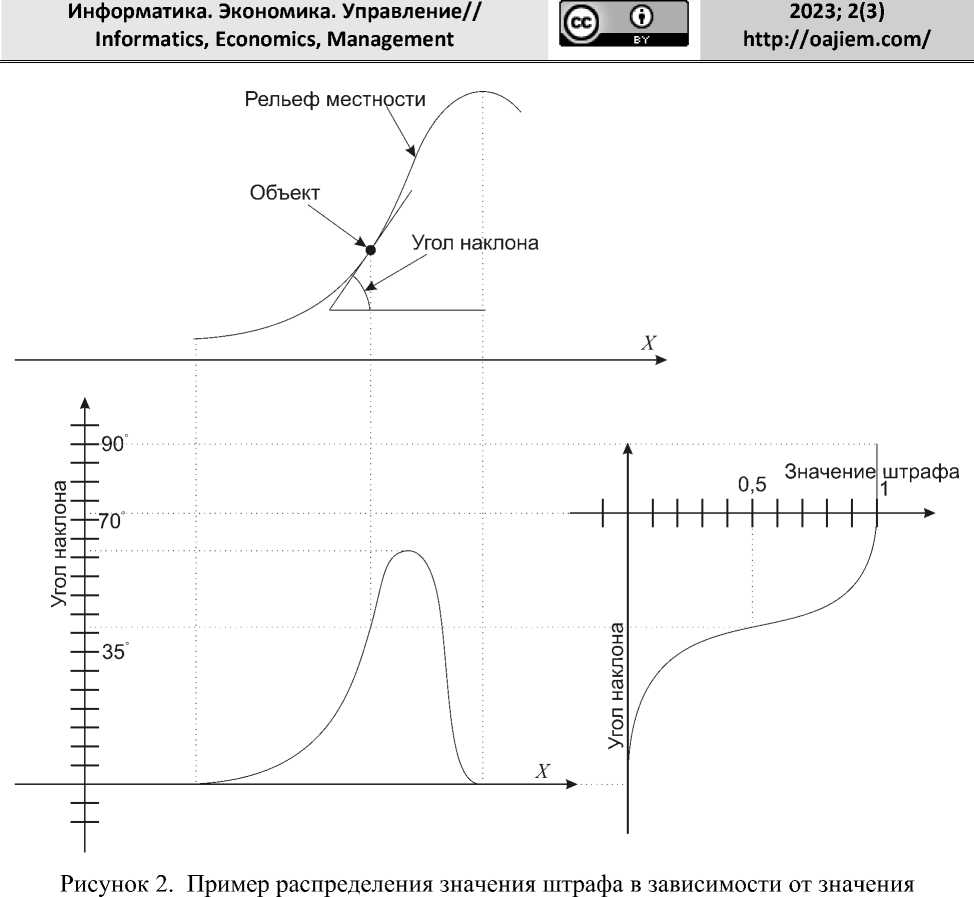
параметра «угол наклона».

• Figure 2.    An example of the distribution of the penalty value depending on the value of the "angle of inclination" parameter.

ПОЛУЧЕНИЕ ИНФОРМАЦИИ

При заполнении матриц зависимости параметров, а также матриц ограничений параметров для обеспечения быстрого поиска значений входных параметров соблюдается следующее. Их значения по каждому из измерений отсортированы по возрастанию, таким образом, обеспечивается единый подход к получению информации о заполненных значениях входных параметров.

Рассмотрим процедуру определения значения параметра по заданным значениями других параметров, в случае, когда известны значения других параметров, лежащие между значениями, указанными в матрицах зависимости. На рисунке 3 приведен пример зависимости значения параметра от двух других параметров.

Практически всегда реальные значения других параметров, применяемых при вычислении значения параметра, не совпадают с теми значениями, которые указаны в матрице зависимости. Таким образом, очевидно, что необходимо вычислять значение параметра путем интерполяции по зарегистрированным значениям в матрице зависимости. Причем интерполяцию целесообразно делать не только линейной (в ряде случаев, и она может легко применяться без ущерба точности), но и применять сплайн интерполяцию со сплайнами нужной степени и вида (квадратичные, кубические, и т.д.).

На рисунке 4 приведены примеры зависимости значения параметра от других параметров при линейной интерполяции (слева) и квадратичной интерполяции (справа). Выбор зависит от необходимой точности, внешних условий, требования по производительности и т.д. Например, динамические параметры системы лучше интерполировать кубическими сплайнами, чем линейными функциями, так как, как правило, в этом случае достигаемая точность выше, и учитываются особенности «поведения» динамических параметров.

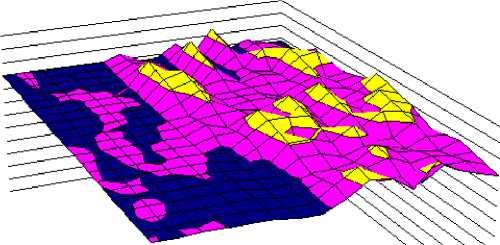
Рисунок 3. Пример зависимости значения параметра от двух других параметров.

Figure 3. An example of the dependence of a parameter value on two other parameters.

Различного рода интерполяции значений выходного параметра по значениям входных требуют различного количества значений входных параметров, но не всегда выборка значений входных параметров обеспечивает требуемое количество. Это происходит, например, по причине малого количества заполненных значений входных параметров в матрице. Для получения необходимой точности выходного параметра достаточно иметь более сложные (точные) интерполяции и проводить их только по наиболее значащим измерениям. А по другим измерениям проводить более простую (линейную) интерполяцию. Таким образом, снижаются требования к количеству значений входных параметров на незначащих измерениях.

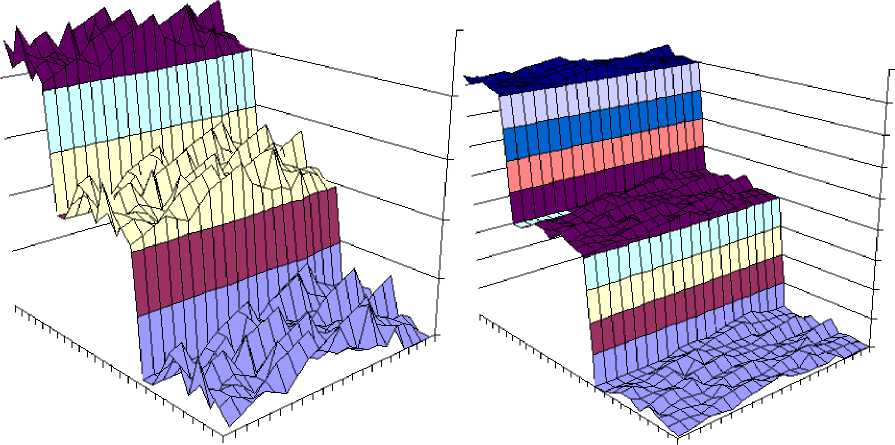
Рисунок 4. Примеры зависимости значения параметра от других параметров при линейной интерполяции (слева) и квадратичной интерполяции (справа).

Figure 4. Examples of the dependence of the parameter value on other parameters for linear interpolation (left) and quadratic interpolation (right).

Для каждого измерения матрицы зависимости возникает необходимость хранения типа (характера) интерполяции значений. Но такую информацию можно установить используемой по умолчанию и указывать, например, для матрицы в целом, а для определенных измерений указывать дополнительно требуемую интерполяцию. Если пойти далее, то для всех матриц зависимости можно принять используемую по умолчанию интерполяцию, а для определенных матриц и их измерений конкретизировать такую информацию, явно указывая используемую интерполяцию.

Такая информация вносится в матрицы зависимости по мере получения информации о значениях входных параметров и каждого выходного параметра, то есть по мере заполнения/оптимизации матрицы зависимости.

В общем случае этот процесс происходит непрерывно. Это неразрывно связано с процессом минимизации информации, хранящейся в матрицах зависимости. Некоторые методы, связанные с оптимизацией транспортно-технологических циклов БПЛА, анализом микропроцессорной производительности при роевом применении дронов-распылителей в точном земледелии, моделированием структур автономных систем и формированием информационных структур для моделирования объектов, сред и процессов, рассматривались ранее в работах [11-14].

ЗАКЛЮЧЕНИЕ

Таким образом, анализ ограничений на значения параметров в пространстве действий автономных интеллектуальных систем является актуальной исследовательской задачей, имеющей значение для развития технологий управления и информационного обеспечения беспилотных летательных аппаратов, как элементов АИС. Так как при функционировании автономных систем в реальных условиях на параметры накладываются ограничения, предложен способ описания ограничений на параметры автономных интеллектуальных систем и дано обобщение информации об ограничениях. Описанная процедура получения информации при заполнении матриц зависимости параметров, а также матриц ограничений параметров необходима для обеспечения быстрого поиска значений входных параметров системы. Предложенный формальный аппарат направлен на минимизацию информации, хранящейся в матрицах зависимости, что будет способствовать, в частности, повышению микропроцессорной производительности при роевом применении дронов-распылителей в точном земледелии, а также эффективному решению других смежных задач, связанных с анализом пространства действий автономных интеллектуальных систем.