К вопросу геометрического проектирования изделий индустрии моды

Методы геометрического моделирования находят самое широкое применение в системах автоматизированного проектирования при решении целого комплекса задач разной степени сложности. К основным задачам автоматизированного проектирования изделий индустрии моды относятся графическое представление нелинейных форм (кривых и поверхностей), а также получение плоских шаблонов (разверток) сложных поверхностей одежды и обуви в трехмерном виртуальном пространстве различными способами. Наиболее распространенными среди инженерных методов получения разверток деталей изделий индустрии моды [1], обеспечивающих максимально высокую точность их построения, являются методы начертательной геометрии [2].

Для развертывания сложной поверхности сложной формы необходимо разделить ее на отдельные участки [3, 4]. Членение поверхности логичнее всего проводить по геодезическим линиям развертывания, в силу ее геометрических свойств. Таким образом, разработка плоских шаблонов участков поверхности - первичных разверток - проводится с помощью проведения геодезических линий развертывания. Но при проектировании изделий индустрии моды конструктивные линии членения исходной поверхности в соответствии с антропологическими и технологическими требованиями зачастую не совпадают с направлением геодезических линий поверхности. Если при разработке швейных изделий (поясных и плечевых изделий) такая необходимость возникает при проектировании основных конструктивных узлов «пройма-рукав», «воротник-горловина», то для проектирования обуви получение плоского отображения негеодезической кривой лежит в основе построения исходного шаблона - развертки обувной колодки. Кроме того, одну и ту же объемную форму можно получить с помощью разнообразных линий членения, несущих, помимо других функций, декоративную нагрузку, весьма значимую именно в случае разработки изделий индустрии моды. К подобным случаям также можно отнести проектирование конфигурации линий деталей подкладки в швейных изделиях на манекенах внутренней формы одежды, градацию сложных контуров деталей при трехмерном моделировании одежды. В некоторых случаях возникает необходимость получе- ния развертки негеодезической кривой, являющейся основообразующей некоторого участка поверхности сложной формы. Например, при трехмерном проектировании головных уборов с различными декоративными членениями, плотно облегающей тело человека спортивной одежды и др. [3].

Моделирование указанных линий, особенно декоративных, на базовых развертках изделия, смоделированных с помощью геодезических линий [4], удлиняет процесс геометрического проектирования и, соответственно, процесс разработки и внедрения изделия. Таким образом, для оптимизации процессов разработки и создания изделий индустрии моды необходим метод, обеспечивающий получение разверток участков поверхности, имеющих сложную конфигурацию, по заданным негеодезическим линиям. В предложенном способе [3] предусмотрено получение развертки детали модели одежды, не очень широкой и имеющей любую заданную конфигурацию. В качестве базовой линии при развертывании деталей данным способом выступает кривая, проведенная внутри контуров каждой смоделированной детали. При этом в данном методе получается сразу готовая деталь конструкции, отпадает необходимость стыковки отдельных элементов и уменьшается трудоемкость процесса получения развертки.

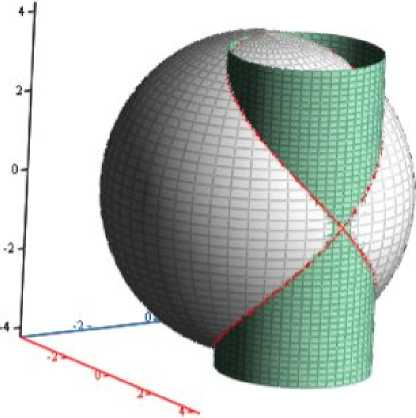
Рис. 1. Кривая Вивиани

Развертка заданной линии сложной конфигурации указанным способом строится с помощью вспомогательной торсовой поверхности, огибающей заданную аналитически сложную поверхность по основообразующей линии сложной конфигурации. Для выделения искомого посредника из возможной конгруэнции торсовых поверхностей выдвинуто утверждение, определяющее построение его ребра возврата [3]. Для проверки выдвинутого утверждения был проведен вычислительный эксперимент на примере кривой Вивиани - линии пересечения сферы и цилиндра с основанием, равным радиусу сферы (рис. 1).

Исходные поверхности задавались в аналитическом виде, а кривая, полученная как линия их пересечения, - в параметрическом виде, наиболее удобном для проведения вычислительных экспериментов. Алгоритм проведенных вычислений представлен на рис. 2.

Для проверки действия способа на реальных поверхностях: твердых - манекенов и колодок, и поверхностях-оболочках изделий из плоских материалов необходимо проведение эксперимента на поверхности, заданной аналитически методом, описанным в работе [5]. Вычислительный эксперимент был проведен в математическом редакторе MathCAD.

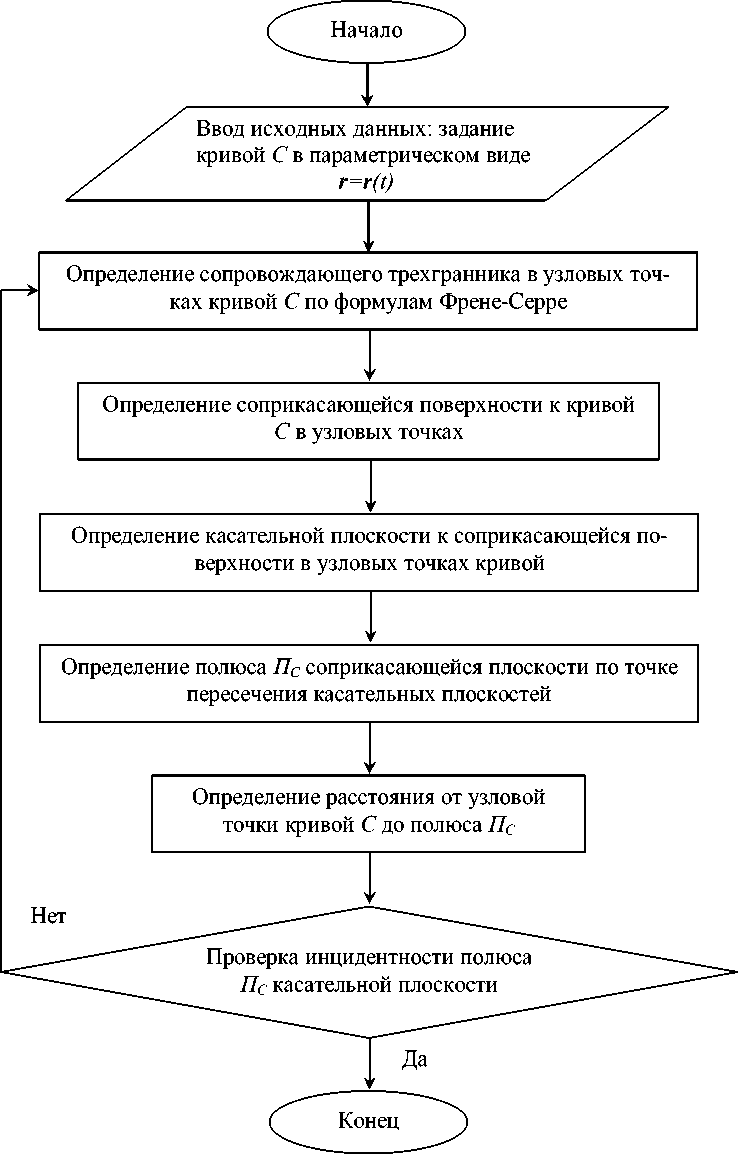
Рис. 2. Блок-схема алгоритма построения ребра возврата торсового посредника

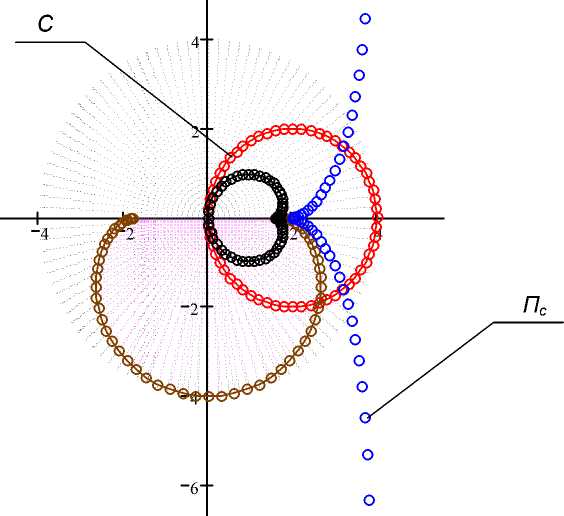
Рис. 3. Вид базовой негеодезической кривой на исходной поверхности С и спроектированного ребра возврата торсового посредника П с в горизонтальной плоскости

Эксперимент подтвердил правильность выдвинутого предположения, что искомая стрикционная линия заданной вспомогательной торсовой поверхности является кривой, образованной множеством полюсов соприкасающихся плоскостей [3]. Последняя является одной из составляющих триэдра Френе-Сорре [6]. Таким образом, математическая модель задания вспомогательной торсовой поверхности D FT может быть представлена формулой следующего вида:

D FT

L([P«S ИF2]), а n

л[ A ]

где - полюс соприкасающейся плоскости в узловой точке базовой кривой;

• - соприкасающаяся поверхность второго порядка;

• n - количество узловых точек;

• a - образующая прямая;

• А - алгоритмическая часть определителя вспомогательного торса [7].

Алгоритмическая часть определителя вспомогательной поверхности А или процесс построения и визуализации торсового посредника задается моделью вида:

^[ AkZM T 1 к л PR, ,.., ,                        (2)

где       Z - задание массива точек базовой линии на трехмерной поверхно-

M _T1_ _k     сти объекта;

PR _V1, ...,п - построение ребра возврата торсового посредника [7].

Перенесение действия алгоритма (рис. 2) графической модели (1) на реальные поверхности изделий индустрии моды позволит оптимизировать решение одной из основных задач проектирования как швейных изделий, так и изделий из кожи (рис. 3 и 4).

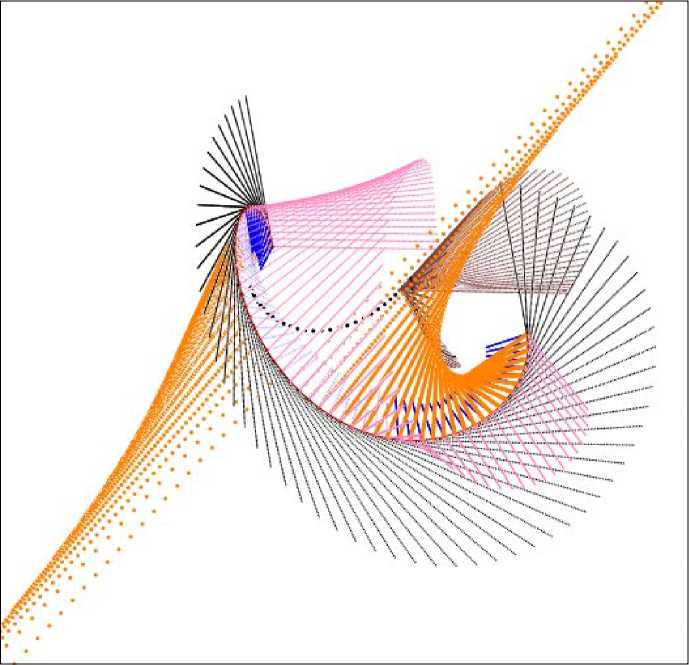
Рис. 4. Пространственное проектирование вспомогательной торсовой поверхности