К вопросу о числе решений транспортной задачи с двумя и тремя поставщиками
Автор: Ассаул В.Н., Погодин И.Е.
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Математическое моделирование и обработка данных
Статья в выпуске: 4, 2024 года.
Бесплатный доступ
В работе даются оценки числа базисных решений транспортных задач (ТЗ) размерности 2хп и 3хп. Исходя из цели получить диапазон изменения числа решений рассматриваются специальные виды задач, дающие наибольшее и наименьшее значения этого диапазона. Для решения поставленной задачи используются комбинаторные методы, метод северо-западного угла с варьированием строк и столбцов, а также методы теории графов. Последние применяются для анализа ситуаций, когда метод cеверо-западного угла не позволяет построить все базисные решения транспортной задачи. Такая ситуация возникает для размерностей 3хк при к>4. Полученные оценки справедливы для произвольного числа n потребителей, занятых в ТЗ. Результаты работы могут оказаться полезными при построении алгоритмов решения широкого класса ТЗ и оценке их сложности.
Транспортная задача, базисный план, мощности поставщиков, емкости потребителей, транспортная таблица, двудольный граф, циклическая перевозка
Короткий адрес: https://sciup.org/148330325
IDR: 148330325 | УДК: 519.8 | DOI: 10.18101/2304-5728-2024-4-39-47
To the question of number of solutions of the transport problem with two or three providers
The paper gives estimates of the number of basic solutions to transport problems of 2xn and 3xn dimensions. Special problems giving a large range of number of solutions are considered, regardless of the type of target function and specific values of costs. To get the estimates the methods of combinatorics and graph theory are used as well as north-west corner method with variation of rows and columns. Results of the presented paper relate to the considered problems with arbitrary amount of consumers and can be used in applications of the approximate methods to the modified transport problems and estimations of their efficiency.
Текст научной статьи К вопросу о числе решений транспортной задачи с двумя и тремя поставщиками
Транспортная задача является классической задачей линейного программирования, находящей немало практических приложений [1-3]. Некоторые ее обобщения имеют нетривиальный характер, что привлекает интерес к построению приближенных решений и оценке сложности применяемых алгоритмов [4-6]. В этой связи важной является информация о числовых характеристиках множества решений, на котором ищется оптимальный план.
Рассмотрим вопрос о числе базисных решений (планов) ТЗ, не уделяя внимания тарифам перевозок. В данной работе мы не ищем оптимальные планы, поэтому стоимость доставки грузов не имеет значения.
Вопрос о числе решений (планов) транспортной задачи уже затрагивался в публикациях [7-9]. Верхней оценкой для числа планов конкретной задачи является число допустимых планов, рассмотренное в работе [9]. Очевидно, это довольно грубая оценка, поскольку учитывает только размерность задачи вне зависимости от количества единиц груза, занятых в перевозках. Представляется интересным уточнить эту оценку и получить диапазон изменения оцениваемой величины с учетом количественных характеристик грузопотока .
Напомним, что базисные решения ТЗ содержат число неизвестных n+m-1, где пхт - размерность ТЗ, а неизвестным соответствуют заполненные клетки транспортной таблицы.
Материалы и методы
В данной работе рассматриваются ТЗ размерности 2хп и 3хп. Начнем с рассмотрения первого случая.
Задача размерности 2хn
Рассмотрим сначала задачу с двумя поставщиками. Число планов для задачи, представленной в табл. 1, равно 6, и это минимально возможная величина для задач такой размерности.
Таблица 1
|
1 |
1 |
1' |
1 |
|
|
2 |
||||
|
2 |
Здесь число планов ограничено минимумом перевозимых грузов, поэтому такие перевозки в дальнейшем рассматривать не будем. В задачах с двумя поставщиками и п потребителями поиск планов облегчают следующие обстоятельства. Здесь возможны два типа планов: вырожденные, с числом заполненных клеток п, и базисные, в которых п+1 заполненная клетка и в одном из столбцов заполнены обе клетки [3]. Число планов при этом определяется числом способов заполнить одну из строк, например верхнюю, вторая строка при этом заполнится автоматически.
В работе [7] отмечалось, что в транспортной задаче тем больше планов, чем меньше вариации в векторах мощностей поставщиков и емкостей потребителей. Это соображение понятно из здравого смысла и легко может быть проиллюстрировано на примере транспортной таблицы (табл.
2, m=203-k), для которой подсчет при к=101, 75, 50 и 25 дает 259, 196, 93 и 26 планов соответственно.
Таблица 2
|
21 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
|
k |
||||||||
|
m |
Таблица 3
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
196 |
|
|
101 |
||||||||
|
m |
В то же время при к=101 и измененном векторе емкостей потребителей (табл. 3) имеем 128 различных планов.
Действительно, в первых семи столбцах может стоять от ноля до 7 единиц, поэтому число планов
N = C 7 0 + C 1 + ... + C 77 = 2 7 = 128. (1)
В случае «симметричной» таблицы (табл. 4) все планы вырожденные, а
N = C 84 = 70.
Таблица 4
|
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
|
|
100 |
||||||||
|
100 |
Уйдя от симметрии и заменив в табл. 4 мощности поставщиков на 99 и 101, получим планы с 9 заполненными клетками, все они содержат один заполненный столбец. В строке с запасом 101 расположатся 4 насыщенные клетки, в другой строке три. Поэтому максимально возможное число планов, а именно это представляет основной интерес данной работы, будет:
N = C 7 4 • 8 = 280.
Для размерности 2хn и небольших вариаций запасов и потребностей имеем диапазон изменения числа планов:
2 n - 1 < N < nCkn - 1 , где k=n/2, (2)
где в случае нецелых чисел следует брать их целые части. Уменьшение числа планов в подобных задачах происходит благодаря появлению вырожденных планов.
Задача размерности 3хn
Рассмотрим задачу с тремя поставщиками. Для задачи размерности 3х3 число планов может быть определено с помощью метода северозападного угла (СЗУ) [3]. Такие планы будем называть «каноническими». Варьирование строк и столбцов определяет 3!х3!/2=18 как максимально возможное число различных планов. Уменьшение этого числа возможно при наличии вырожденных планов и других планов специального вида.
Для задач с минимальной вариацией данных, а именно такие, как уже отмечалось, дают максимальное число планов, верхней границей служит число 18. В случае одинаковых мощностей и емкостей (табл. 5) все планы вырожденные и имеют по 3 заполненные клетки, на 2 меньше, чем требует условие базисности. Всего таких планов 6.
Таблица 5
|
k |
k |
k |
|
|
k |
|||
|
k |
|||
|
k |
Таблица 6
|
1 |
1 |
52 |
|
|
18 |
|||
|
18 |
|||
|
18 |
Рассмотрим задачу типа той, что представлена в табл. 3 (табл. 6). В этой задаче будет 9 планов, поскольку третий столбец всегда заполнен, а в первых двух по одной заполненной клетке. Таким образом, имеем следующий диапазон изменения числа планов:
9 ≤ N ≤ 18.
Для задачи c числом потребителей большим трех ситуация усложняется, поскольку не все планы могут быть получены варьированием в рамках метода СЗУ. Такие планы будем называть «неканоническими». Как отмечалось в [9], аналогия с двудольными графами позволяет установить, что граф, содержащий подграф, показанный на рис. 1, не может быть построен с помощью метода СЗУ.
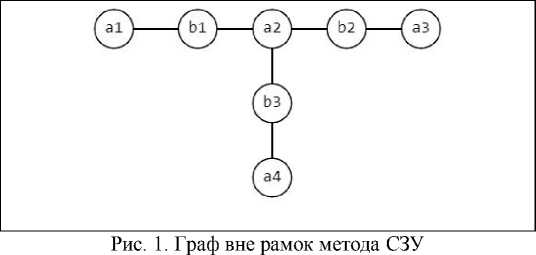
На рис. 1 вершины с буквой a относятся к потребителям, а с буквой b к поставщикам. Две вершины соединены ребром, если соответствующие клетки транспортной таблицы заполнены, то есть ребра графа соответствуют заполненным клеткам транспортной таблицы.
Применительно к задаче определения числа планов это означает, что потребитель a 2 связан с тремя поставщиками, то есть в транспортной таблице имеется полностью заполненный столбец. С другой стороны, есть 3 концевые вершины. Им соответствуют насыщенные клетки транспортной таблицы. Пример такого плана для задачи размерности 3х4 показан в табл. 7.
Таблица 7
|
3 |
3 |
3 |
3 |
|
|
4 |
3 |
1 |
||
|
4 |
1 |
3 |
||
|
4 |
1 |
3 |
Таблица 8
|
3 |
3 |
3 |
3 |
|
|
4 |
3 |
1 |
||
|
4 |
2 |
2 |
||
|
4 |
1 |
3 |
Число таких планов равно:
N = 4 ■ C 1 • C 2 = 24.
Это число нужно добавить к «каноническим» планам из метода СЗУ. Заполнение табл. 7 по методу СЗУ дает следующий план (табл. 8). С другой стороны, задача, подобная плану, представленному в таблицах 3 и 6, дает 27 различных планов . Таким образом, число планов для задачи 3х4 заключено в диапазоне:
27 ≤ N ≤ 96.
Следуя выбору задач с наибольшим числом планов, будем рассматривать равные мощности потребителей и равные емкости потребителей. Случай кратности чисел n и m (например, 3 и 6) приводит к образованию вырожденных планов, поэтому для определения максимального числа планов он не интересен. Наличие «неканонических» планов увеличивает число базисных планов, поэтому такие случаи представляют отдельный интерес.
В табл. 9-14 приведены транспортные таблицы размерности 3х5 (табл. 9), 3х7 (табл. 10, 11), 3х8 (табл. 12), и 3х13 (табл. 13, 14) и примеры их заполнения. Планы 3х5 и 3х8 имеют лишь «канонические» планы, число которых определяется варьированием строк и столбцов транспортной таблицы. Планы 3х7, 3х13 и вообще планы размерности 3хn, где n=1 (mod3), имеют и «канонические» и «неканонические» планы.
Таблица 9
|
3 |
3 |
3 |
3 |
3 |
|
|
5 |
3 |
2 |
|||
|
5 |
1 |
3 |
1 |
||
|
5 |
2 |
3 |
Таблица 10
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
7 |
3 |
3 |
1 |
||||
|
7 |
2 |
3 |
2 |
||||
|
7 |
1 |
3 |
3 |
Таблица 11
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
7 |
1 |
3 |
3 |
||||
|
7 |
1 |
3 |
3 |
||||
|
7 |
1 |
3 |
3 |
Таблица 12
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
8 |
3 |
3 |
2 |
|||||
|
8 |
1 |
3 |
3 |
1 |
||||
|
8 |
2 |
3 |
3 |
Таблица 13
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
13 |
3 |
3 |
3 |
3 |
1 |
||||||||
|
13 |
2 |
3 |
3 |
3 |
2 |
||||||||
|
13 |
1 |
3 |
3 |
3 |
3 |
Таблица 14
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
|
13 |
1 |
3 |
3 |
3 |
3 |
||||||||
|
13 |
1 |
3 |
3 |
3 |
3 |
||||||||
|
13 |
1 |
3 |
3 |
3 |
3 |
Подсчет с учетом последних планов дает следующие величины.
Для задачи 3х5: N = 5 • C 4 • C 11 • C 2 • 3 = 360 .
Для задачи 3х7: N = 7 • C 62 • 4 • 3 • 3 + 7 • C 62 • C 4 2 = 3 780 + 63 0 = 4410.
Для задачи 3х8: N = 8 • C 7 2 • 5 • C 42 • 3 = 15120.
Для задачи 3х13: N = 13 • C ,4 2 • 8 • C 7 3 • 3 + 13 • C 42 • C 8 4 = 5855850 .
Исходя из сказанного, можно предложить следующую формулу для диапазона изменения числа планов транспортной задачи размерности 3хn при наличии «неканонических» планов:
3 n - 1 < N <= 3 n • C - • ( n - k - 1) • C - k - 2 + n • C - 1 • C - k - 1 , (3)
где k — целая часть отношения n/3.
Отношение второго слагаемого (3) к первому равно дроби:
1/3 ⋅ ( n - 2 k - 1). (4)
Подставляя приближенно k=n/3, получим затухание второго слагаемого сравнительно с первым обратно пропорционально n. Это говорит о том, что при больших n «неканоническими» планами в формуле (3) можно пренебречь.
Полученная оценка позволяет оценить число планов различных модификаций транспортных задач с двумя и тремя поставщиками (либо с двумя и тремя потребителями), что важно для оценки трудоемкости вычислений и выбора алгоритма решения задачи.
Выводы
В работе проанализированы количественные и качественные характеристики множества допустимых планов ТЗ, которые могут быть полезны при решении различных типов ТЗ, а также при оценке числа базисных планов ТЗ в модифицированной постановке, отличной от классической. Даны оценки числа «неканонических» планов, обладающих более сложной графической структурой.
Список литературы К вопросу о числе решений транспортной задачи с двумя и тремя поставщиками
- Сигал И. Х., Иванова А. П. Введение в прикладное и дискретное программирование: модели и вычислительные алгоритмы. Москва: Физматлит, 2007. С. 45-49.
- Цыплакова О. Н., Цысь Ю. В., Кобылина А. В. Транспортная задача и её применение в решении экономических задач // Современные наукоемкие технологии. 2014. Ч. 2, № 5. С. 178-180. EDN: SALXRF
- Фролькис В. А. Введение в теорию и методы оптимизации для экономистов. Санкт-Петербург: Питер, 2002. 320 с. EDN: ULAZJT
- Balinski M. L. Fixed cost transportation problem // Naval Research Logistics Quaterly. 1961; 8 (1): 41-54.
- Ассаул В. Н. Погодин И. Е. Об одном практическом способе решения транспортной задачи с "экологическим" критерием // Вестник Бурятского государственного университета. Математика и информатика. 2022. № 3. С. 3-13. DOI: 10.18101/2304-5728-2022-3-3-13 EDN: HYPCEB
- Ассаул В. Н., Погодин И. Е. Об упрощениях решения транспортной задачи с экологическим критерием // Экономика и математические методы. 2023. Т. 59, вып. 2. С. 122-127. DOI: 10.31857/S042473880025864-9 EDN: LBAZYS
- Погодин И. Е. О способах оценки числа планов транспортной задачи // Экономика и математические методы. 2020. Т. 54, вып. 4. С. 116-120. DOI: 10.31857/S042473880012408-7 EDN: GMBEAA
- Ассаул В. Н., Погодин И. Е. Вырожденные планы и декомпозиция транспортной задачи // Известия высших учебных заведений. Серия: Экономика, финансы и управление производством. 2024. № 2 (60). С. 55-60. EDN: NPNIOP
- Ассаул В. Н., Погодин И. Е. Допустимые планы в транспортной задаче // Вестник Бурятского государственного университета. Математика, информатика. 2024. № 2. С. 13-21.
