К вопросу о локальном расширении группы параллельных переносов трехмерного пространства

• 1.    Введение

• 2.    Основные определения

В работе В. В. Горбацевича [1] приводится определение расширения транзитивной группы Ли G, действующей в многообразии M : расширением транзитивной группы Ли G называется группа Ли G 1 , содержащая G в виде подгруппы Ли и тоже транзитивная на M , причем ограничение этого транзитивного действия на G дает исходное транзитивное действие группы Ли G. Классическим примером расширения группы параллельных переносов пространства R ³ является группа аффинных преобразований этого же пространства. Также отметим, что в работе [1] рассматриваются глобальные действия и приводится алгебраическая конструкция, дающая расширения транзитивных действий разрешимых групп Ли на компактных многообразиях.

Согласно монографии Г. Г. Михайличенко [2] можно говорить, что локально просто транзитивная группа Ли преобразований пространства R ³ задает феноменологически симметричную геометрию двух множеств ранга (2, 2), а локально дважды транзитивная группа Ли преобразований пространства R ³ задает феноменологически симметричную геометрию двух множеств ранга (3, 2). Отметим, что первым множеством является пространство R ³ , а вторым множеством является транзитивно действующая группа Ли G.

В данной работе ставится задача о нахождении всех локальных дважды транзитивных расширений группы параллельных переносов пространства R ³ . Эти группы Ли преобразований шестимерные и задают феноменологически симметричные геометрии двух множеств ранга (3, 2). В данной статье проводятся исследования алгебр Ли таких расширений. Базис алгебр Ли состоит из системы шести операторов X 1 , X 2 , X 3 , Y 1 , Y 2 , Y 3 , причем X i = d x , X 2 = d y , X 3 = d z задают базис группы параллельных переносов. Из условия замкнутости коммутаторов [X i ,Y j ], где i,j = 1, 2, 3, записываются три системы дифференциальных уравнений на коэффициенты операторов Y 1 , Y 2 , Y 3 . Матрицы коэффициентов этих систем можно упростить приведением их к жордановым формам. Также доказывается, что эти матрицы должны коммутировать между собой, что приводит к существенному упрощению их вида.

Нахождение явных действий локальных дважды транзитивных расширений группы параллельных переносов пространства R ³ является объемной задачей и предполагается оформить ее отдельной статьей.

Отметим, что проводимые здесь исследования апробированы в работе [3] на примере классификации локальных дважды транзитивных расширений группы параллельных переносов плоскости R ² .

Сначала определим локальное действие класса C ² группы Ли G, причем dim G = n, в пространстве R ³ , которое приводим согласно работе [4].

Определение 1. Дифференцируемое класса C ² отображение п: R ³ х G ^ R ³ называется эффективным локальным действием , если выполняются следующие свойства:

• 1 ° . п(а, e) = а для всех a G W , где W — область в R ³ , e G G — единица;

• 2 ° . п(п(а, h i ), h ₂ ) = п(а, h1 h ₂ ) для всех a G W , где h1, h ₂ G G;

• 3 ° . п(а, h) = а для всех a G W , где h G G, тогда и только тогда, когда h = e;

• 4 ° . n h : R ³ ^ R ³ — локальный диффеоморфизм для всякого h G G.

Тройка (R ³ ,G, п) называется локальной группой Ли преобразований многообразия R ³ .

Обозначим через L алгебру Ли данной группы преобразований. Базис этой алгебры Ли состоит из операторов:

Z i = Zd + z 2 d y + Z 3 d z ,                          (1)

где i = 1,..., n.

Определение 2. Эффективное локальное действие п: R ³ х G ^ R ³ называется дважды локально транзитивным , если дополнительно выполняются свойства:

• 5 ° . n = 6;

  /Z 1 (a)		Z 12 (a)	Z 13 (a)	Z 11 (b)	Z 12 (b)	Z 3 (b)\
  	Z 21 ( a )	Z 22 (a)	Z 2 3 (a)	Z 21 (b)	Z 22 (b)	Z 23 (b)
  V=	Z 31 ( a ) Z 41 ( a )	Z 32 (a) Z 42 (a)	Z 33 (a) Z 43 (a)	Z 31 (b) Z 41 (b)	Z 32 (b) Z 42 (b)	Z 33 (b) Z 43 (b)	,                         (2)
  	Z 5 ( a )	Z 52 (a)	Z 53 (a)	Z 51 (b)	Z 52 (b)	Z 53 (b)
  \ Z^a)		Z 62 (a)	Z 63 (a)	Z 61 (b)	Z 62 (b)	Z 63 (b)

  6 ° . Матрица

  
  

составленная из коэффициентов операторов (1) невырождена для любых точек некоторых окрестностей U (a ' ),U(b ' ) С W .

Свойства 5 ° и 6 ° равносильны тому, что действие п х п в R ³ х R ³ локально просто транзитивно.

Определение 3. Будем говорить, что дважды локально транзитивное действие п: R ³ х G ^ R ³ является локальным расширением группы параллельных переносов, если базис ее алгебры Ли L состоит из операторов

X 1 = d x , X 2 = д у , Х з = d z , Y i = A i d x + B i d y + C i d z ,

причем A i = A i (x,y,z) B i = B i (x,y,z), C i = C i (x,y,z) — дифференцируемые функции класса гладкости C 1 , где i = 1, 2, 3.

В таком случае в алгебре Ли L выделяется коммутативная трехмерная подалгебра J , образованная операторами X 1 , X 2 и X 3 . Произвольный оператор Y является линейной комбинацией с постоянными коэффициентами базисных операторов.

Теорема 1. Локальное действие п: R ³ х G ^ R ³ с операторами ее алгебры Ли (3) локально дважды транзитивно тогда и только тогда, когда матрица

K (b) - K (a)

невырождена, где

( A i (Х а , У а , Z a ) B 1 (X a ,y a ,Z a ) C 1 (X a ,y a ,Z a ) A 2 (X a ,y a ,Z a ) В2(Х а ,У а , Z a ) С2(Х а ,У а , Z a ) A3(X a ,y a ,Z a] B3(X a ,y a ,Z a ) Сз(Х а ,У а , Z a )

причем a = (x _a ,y _a ,z _a ) G U (а ' ) С W С R ³ .

<1 Матрица (2) для действия п : R ³ х G принимает следующий вид:

V = ( E

V к (а)

^ R ³ с операторами ее алгебры Ли (3)

E )

K(b)) ,

где E — единичная матрица 3 х 3. Согласно формуле Шура [5, с. 59] | V | = | K(b) — K (а) | . Если действие п : R ³ х G ^ R ³ дважды локально транзитивно, то | V | = 0, и поэтому | K(b) — K (а) | = 0. Справедливо и обратное. >

Из доказательства этой теоремы вытекает следующее утверждение.

Следствие 1. Локальное действие п : R ³ х G ^ R ³ с операторами алгебры Ли вида

(X i = d x , Х 2 = д у , Х 3 = d z , Y 1 = A i (x,y,z)d x + B i (x,y,z)d y ,

(Y2 = A2(x,y,z)dx + B2(x,y,z)dy, Y3 = A3(x,y,z)dx + B3(x,y,z)dy не является локально дважды транзитивным.

3. Системы линейных уравнений

Из свойства замкнутости относительно операции коммутирования, превращающей векторное пространство операторов в алгебру Ли, следует, в частности, что и коммутаторы [X j , Y k ], где j, k = 1, 2, 3, принадлежат этой же алгебре Ли [6]. В координатной записи, с учетом (3), это свойство приводит к системе дифференциальных уравнений на коэффициенты A i , B i , C i :

dAi = V п3 А- 4- л 1   dAi = V hj А • 4- n 1   dAi = V j A ■ 4- dx     Z—i ai Aj + gi ,    dy     A-< bi Aj + pi ’    dz     A-< ci Aj + j=1                      j=1

3                             33

dB = V ajBj + g2 dB = V bj b, + ■ ■ dB = V cjBj + q2,(7)

j=1                      j=1

dCi _ V Лл. I „3   SC _ V jlfi. „3   SC _ V .7 • dx =    ai Cj + gi,   dy = bi Cj + pi,   dz = ci Cj j=1                     j=1

причем a ^j , b j , c ^j , g j , q j , p ^j = const, i,j = 1, 2, 3. Введем

матричные

обозначения:

a ¹ ₁ a ¹2 _a 1₃

a ² ₁

a ² ₂

_a 2₃

a ₁                  b ₁

^a 3 I , T 2 = I ^b 2

_a 3_{3                 b} 1₃

b ²1

b ²2

_b 2₃

b ³1

b2 I , _b 3₃

1 c ₁ c ¹2

1 c ₃

2 c ₁

2 c ₂

2 c ₃

c ₁

3I c2    , c3

Тогда система (7) в матричном виде принимает простой вид:

'A . = TIA + A 1 , A , = t₂ A + P 1 , A z = T3A + 4 1 ,

■ Ax = T1A + A2, Ay = T2p + A2, Az = T3A + A2,(8)

A x = T1^A + ^A 3 , ^A y = T 2 ^p + ^A 3 , ^A z = T3^A + A 3 .

Из свойства независимости частных производных относительно порядка дифференцирования вытекают соотношения:

' (T1T2 - T2T1)P = P1, (T1T3 - T3T1)P = P2, (T3T2 — T2T3)P =

< (T1T2 - T2T1)P = P4, (T1T3 - T3T1)P = P5, (T3T2 - T2T3)P = P6,(9)

_ (T1T2 - T2T1)P = P7, (T1T3 - T3T1)p = p8, (T3T2 - T2T3)P = где R 1, . . . , R9 — некоторые постоянные векторы. Линейные системы (9), очевидно, совместны.

Теорема 2. Подалгебра Ли J алгебры Ли L является идеалом тогда и только тогда, когда векторы A _x , B _x , C _x , A _y , B _y , C _y , A _z , B _z , C _z постоянные.

⊳ Пусть сначала J — идеал в L. Заметим, что J — идеал тогда и только тогда, когда

[Xi, Yk] = M1X1 + №X2 + ^3X3, причем ^1,^2,^3 = const, i, k = 1, 2, 3. Тогда px, px, px, py, py, py, pz, pz, pz — константы.

Обратно, пусть производные коэффициентов операторов Y 1 , Y 2 и Y 3 постоянны. Тогда коммутаторы [X i , Y k ] будут линейно выражаться через операторы X i , X 2 и X 3 , поэтому J — идеал в L. ⊲

Из доказательства этой теоремы вытекает

Следствие 2. T i = T 2 = T 3 = 0 тогда и только тогда, когда J — идеал в L.

• <1 Если T i = T 2 = T 3 = 0, то из системы (8) получаем A x = const, B _x = const, C _x = const, A _y = const, B _y = const, C _y = const, A _z = const, B z = const, C _z = const и поэтому J — идеал в L (теорема 2).

Пусть J — идеал в L. Предположим для определенности T i = 0. Тогда, согласно системе (8), хотя бы одна из производных A _x , B _x , C _x не постоянна. Поэтому, согласно теореме 2, получаем, что J не является идеалом в L. Получили противоречие. ⊲

Теорема 3. Матрицы коэффициентов системы (8) взаимно коммутативны, т. е.

T 1 T 2 - T 2 T 1 = T 1 T 3 - T 3 T 1 = T 3 T 2 - T 2 T 3 = 0.

• ⊳ Пусть одна из пар матриц коэффициентов системы (8) некоммутативна, т. е. T 1 T 2 — T 2 T 1 = 0. В таком случае ранг матрицы T 1 T 2 — T 2 T 1 равен либо 3, либо 2, либо 1. Эквивалентными преобразованиями добиваемся упрощения систем линейных уравнений

(T 1 T 2 — T2Ti)l = » i , (T 1 T 2 — T2Ti)l = » 4 , (T 1 T 2 — T 2 T i ) ^ = ^А 7 .

Тогда в эквивалентных системах матрица коэффициентов принимает вид

T 1 T 2 — T 2 T 1 =

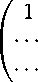
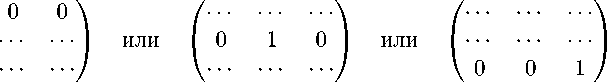
Значит, A i = const, B i = const, Ci = const или A 2 = const, B 2 = const, C 2 = const или A 3 = const, B 3 = const, C 3 = const. Поэтому, соответственно, оператор Y i , или Y 2 , или Y 3 из системы (3) линейно выражается через операторы X 1 , X 2 и X 3 , что противоречит линейной независимости базисных операторов (3). Аналогичная проверка проводится и относительно систем из (9) с матрицами коэффициентов T 1 T 3 — T 3 T 1 и T 3 T 2 — T 2 T 3 . >

Теорема 4. Для алгебры Ли локально дважды транзитивного действия п : R ³ х G » R ³ в подходящем базисе матрица T принимает жорданов вид

/А 0  0\        /А 1  0\       /А 1  0\        /Ai  0   0А

• 1)    0 А  0   ;   2)    0 А  0   ;   3)   0 А  1   ; 4)     0   Ai   0;

00А      00А      00А      00А

/А1   1   0 \        /А1  0   0 \        / а   в0\

• 5)    0 А 1 0 ; 6)    0 А 2 0   ; 7)     — в а 0 ,

\ 0   0  А2/       \ 0   0  Аз/       \ 0   0

причем а, в, А, А 1 , А 2 , А з — константы, в = 0, А 1 = А 2 , А 1 = А з , А 2 = А 3 .

• <    Базис алгебры Ли локально дважды транзитивного действия п : R ³ х G ^ R ³ задается операторами (3). Переходим к новому базису X i ’ = X i , У- = ^ 3=1 X j Y j , причем матрица коэффициентов х = (x^j) невырождена. Тогда выражения (3) принимают следующий вид: X i = д _ж , X 2 = d y , X 3 = д _г , У/ = A ’ d ^ + B i d y + C i d z , причем

  A » = х А .   ^ = x S .  ? = x ^ .

  
  
  
  

Далее, вычисляя коммутаторы [X i , Y j ' ], учитывая их замкнутость и сравнивая коэффициенты перед ∂ _x , ∂ _y и ∂ _z , получаем векторные уравнения

'^ x = T i А ’ + G ’^   A ’ y = T 2 A ’ + P ^ 1 , < B‘x = T{ B ‘ + G ‘2,   B ‘y = T 2 B ‘ + P ‘2, c ’ x = T ‘ c' + G ’ 3 ,   c'y = T 2 c' + p ’ 3,

j ' z = T 3 A ' + Q '\ в', = T 3 в' + S ' 2 , C', = T ' C ' + Q '3.

В последнюю систему подставляем выражения (11) и сравниваем с (8), имеем

T 1 = X - 1T1X, T 2 = X — 1 T 2 X, Т з = X — 1 T 3 X.

В линейной алгебре доказывается, что подбором невырожденной матрицы χ матрицу T 1 можно привести к жордановому виду [7, с. 482], т. е. приходим к утверждению теоремы. ⊲

Теорема 5. Пусть матрица Ti имеет жорданов вид (10). Тогда произвольная комму тативная с ней матрица T принимает следующий вид:

a1 a2 aa a4 a5 a6 I ; 2) I 0

a7 a8 а9/\ 0

a1 a2

0 ai 0;

0   0a

a2  a             a1

ai   0   ;   3)    0a a8  a9            00

/ai   00

6)   0   a5   0   ;7)

\ 0   009/

as \        (a _i a2 0

a ₂ ; 4) a 4 a 5 0

ai           00 a ai a2

—a2 a i 0 I .

0    0a

⊳ Доказательство этой теоремы сводится к вычислению матричных коммутаторов и приравниванию их к нулевой матрице: T i T — TT i = 0. Проиллюстрируем этот алгоритм для третьего случая, т. е. когда матрица T 1 имеет вид 3) из (10), а матрица

T=

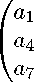
a 2

a 5

a 8

a 3 a 6

a 9

Тогда получаем

T _i T — TT _i =

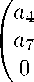
a5 — ai a8 — a4

— a 7

a 6 — a 2

a 9 — a 5

= 0.

— a 8

Видно, что a 4 = a 7 = a 8 = 0, a 5 = a 9 = a i , a 6 = a 2 . В результате матрица T принимает вид 3) из (12). ⊲

Теоремы 3, 4 и 5 дают существенные ограничения на матрицы коэффициентов T 2 и T 3 из системы (8).

Теорема 6. Возможны только следующие неупорядоченные тройки значений для матриц T 1 , T 2 и T 3 :

Z Ai   0   0\    Z^i   0   0\   Zvi  00\

I 0    Аз    0 I ,  I 0    №з    0 I ,  I 0    V2    0 I;

у 0   0  Азу    у 0   0  №3у    у 0   0V

^A i ^А з ⁰ \ Z^i № 0 A i 0 , 0 № i 0 0 А2У \0 0

µ 2

ν 3 ν 1

⁰ I , ^А з + ^№ 2 + ^v 3 = ^0;

ν 2

λ 1 λ 2

0 λ 1

А з \ λ 2 λ 1

µ 1 µ 2 µ 3

0 µ 1 µ 2

0   0  µ 1

ν 1 0 0

ν 2 ν 3

ν 1 ν 2

0   ν 1

λ ² ₂ + µ ² ₂ + ν ₂ ² = 0;

λ 1 λ 2    0

I —^2 A i 0 I

0    0  λ 3

µ 1

— №

µ 2

µ 1 0

µ 3

^ν 1    ^ν 2    0

• ^—v 2   ^v i   о I, a 2 + ^ 2 + ^v 2 = o;

0    0  ν 3

λ 1  0      µ 0  µ2      ν ν1

0 λ  0   ,    0 µ   0   ,   0 ν   0   , µ2

00λ   00µ   00ν

λ 1  0      µ 0  µ2      ν ν1

0λ0,    0µ0   ,   0ν   0.

00λ   01µ   01ν

⊳ Приведем схему нахождения матриц T 1 , T 2 и T 3 .

• а)    Берем матрицу T 1 . Затем, согласно теореме 5, записываем соответствующую коммутативную с ней матрицу T 2 .

• б)    Упрощаем матрицу T 2 с помощью допустимой матрицы χ: χ ^{- 1} T 2 χ. Допустимая матрица χ — это произвольная невырожденная матрица, сохраняющая матрицу из списка (10): T 1 = χ ^{- 1} T 1 χ. По сути она вычислена в теореме 5:

  b1   b2

  1) x = I b 4   b 5   Ь б I ;

  b7  b8

  b1   b2

  3) χ =   0   b1  b2

  0   0b

  /bi  b2   о \/

  • 5)    χ =   0  b1  0   ;  6) χ =0

  0   0  b9

  
  

  • b1   b2

  • 2)    x = I 0   bi   0 I

  0   b8

  • (bi  b2о

  4) χ =   b4  b5   0;

  0   0b

  0   0 ^{\              /} b i    b 2 0 ^\

  b5 0   ;   7) x = —b2 bi 0.

  0   b9                   0    0b

  
  
  
  

• в)    Вычисляем матрицу T 3 , коммутативную с матрицами T 1 и T 2 .

• г)    Упрощаем матрицу T 3 с помощью допустимой матрицы ω: ω ^{- 1} T 3 ω, т. е. произвольной невырожденной матрицы, для которой T 1 = ω ^{- 1} T 1 ω, T 2 = ω ^{- 1} T 2 ω.

  Продемонстрируем эту схему на следующем примере.

  
  

  / A i

  а) Пусть T 1 =   0

  
  

0 0                                                    a 1

λ 1 0 , λ 1 = λ 2 . Согласно теореме 5 имеем T 2 = a 3

0 λ 2                                                  0

a 2

a 4 0

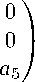
• б)    Матрица χ принимает вид 4) из (13). Упрощая матрицу T 2 (χ ^{- 1} T 2 χ), получаем

  T 2 =

  
  

  a 1 0 0

  
  

  0   0a

  a1   0    ;0

  0   a5

  
  

  0   0a

  a2   0   ;0

  0  a5

  
  

  a 1 0

  
  

  0 I;

  a 5

  

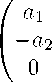
  a 2

  a 1 0

  
  

  a 5

  
  

  • в)    Согласно теореме 5, соответственно получаем

  
  

  T 3 =

  c 1	c 2	0	c 1	0	0	c 1	c 2	0	c 1	c 2	0
  c 3	c 4	0);	0	c 2	0);	0	c 1	0);	— c 2	c 1	0
  0	0	c 5	0	0	c 5	0	0	c 5	0	0	c 5

  .

  
  

  • г)    Допустимая матрица ω соответственно равна

  
  

  d1  d2   0d

  d3  d4   0   ;0

  0   0  d5

  
  

  0   0       d1  d2   0        d1   d2

  d2    0  I ; I  0   di    0  I ; I —d2   di   0I

  0   d5       0   0  d5        0    0d

  
  

  det ω = 0.

  
  

  Далее, упрощая матрицу T 3 с помощью ω , получаем

  
  

  c1   0   0        c1   0   0        c1   1   0         c1    c2

  T3 = 10   c1   01; 10   c2   0   ;     0   c1   0   ; I —°2   c101;

  0   0  c5       0   0  c5       0   0  c5        0    0c

  
  

  c1   00

  T3 =   0  c2  0;

  0   0c

  c1  c2

  0   c1   0;

  0   0c

  • c1 c2

  • ^—c 2 c i 0 I .

  0    0c

  
  

  Рассмотрим еще один пример.

  
  

  / A i

  • а) Пусть T 1 =   0

  
  

  λ 1 0   . Тогда согласно теореме 5

  0 λ 1

  
  

  T 2 =

  
  

  a 1 0 0

  
  

  a 2

  a 1

  a 4

  
  

  a 3 0

  a 5

  
  

  • б)    Матрица χ принимает вид 2) из (13). Упрощая матрицу T 2

  
  

  (χ ^{- 1} T 2 χ), получаем

  
  

  результаты при a 1 = a 5

  
  

  a 1 0 0

  
  

  a 2

  a 1 0

  
  

  0 ) ’

  a 5

  
  

при a 1 = a 5

T 2 =

a 1 0 0

a 2

a 1 0

a 1

a 1 0 0

0   a3                a1

a1   0   , a3 = 0;    0a

0   a1                 01

a 3 0

a 1

• в)    Из условия коммутативности матрицы T 3 с матрицами T 1 и T 2 , соответственно получаем при a 1 = a 5

c1  c2

0   c1   0;

0   0c при a1 = a5

c 1

T 3 =  0

c 2 c 1

c 4

c3       c1

0    ;    0c c5       00

c3       c1  c2

0   ;    0   c1

c1        0   c4

• г)    Допустимая матрица ω соответственно равна при a 1 = a 5

d1 d2

0 d1 0   ,  det ω =0;

0   0d при a1 = a5

d 1 0 0

d 2 d 1

d 4

d3

0;0

d5

d2  d3       d1  d2

d1   0   ;    0   d1

0  d1       0   d4

det ω = 0.

Далее, упрощая матрицу T 3

с помощью ω , получаем при a 1 = a 5

c 1

T 3 =  0

c 2

c 1 0

0 ), c 5

при a 1 = a 5

c1  c2   0c

0   c1   0   ;0

0   0   c1

0   c3                c1   0c c1   0   , c3 = 0;    0   c1   0;

0   c1                  0   1c

c 1

T 3 =  0

/c i

T 3 =  0

c 2

c 1 0

c 2

c 1

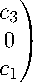
c 3

c 1

Остальные случаи рассматриваются аналогично. Группируя полученные результаты, приходим к утверждению теоремы. ⊲

В конце отметим, что при доказательстве теорем 5 и 6 для упрощения расчетов использовался пакет математических программ Maple 17 [8].

4. Заключение

Решенная здесь задача является частью задачи классификации локально дважды транзитивных групп Ли преобразований пространства R ³ , являющихся расширениями группы параллельных переносов этого же пространства. Для дальнейшего решения классификационной задачи необходимо по решениям системы дифференциальных уравнений (8) записать алгебры Ли локально дважды транзитивных групп Ли преобразований пространства R ³ , после чего, применяя экспоненциальное отображение, найти их локальные действия.