К вопросу о моделировании трендов временных рядов

При анализе и построении моделей временных рядов (ВР), отражающих как циклическое, так и трендовое изменение интересующей величины, чаще всего на первом этапе выделяют отдельные компоненты модели в соответствии с имеющимися в наблюдениях исходными данными, а затем эти компоненты (кроме случайной) используют для прогнозирования. Выделение компонент в простейших случаях рассматривают в концепции тренд-сезонного моделирования в виде аддитивной (1) или мультипликативной (2) моделей [1; 3; 7; 8]:

y = T + S + E ,               (1)

y = T • S ■ E ,                    (2)

где T — тренд, который будем пока считать линейным: T = a + bt ;

S — циклическая компонента ВР;

E — остаточная компонента.

В   [3] предлагается такая последо вательность анализа аддитивной модели ВР:

• 1.    Выравнивание данных исходного ВР (методом скользящей средней).

• 2.    Расчёт значений S .

• 3.    Расчёт значений T + E = y — S .

• 4.    Расчёт T .

• 5.    Расчёт значений T + S .

• 6.    Расчёт и анализ E .

Естественно, что под результатами расчётов понимаются не сами значения компонент и параметров модели (они не наблюдаемы), а их оценки.

К одним из недостатков этого подхода можно отнести то, что в ходе шага 1 приходится терять часть исходной информации на фильтрацию циклической компоненты методом скользящей

средней, а эти потери могут снизить точность расчётов как в шаге 2, так и неизбежно в последующих шагах. Особенно остро этот недостаток отражается при малом объёме выборки (как по числу циклов, так и по числу наблюдений за один цикл).

Другим недостатком следует считать то, что, как правило, метод требует очень большого количества исходной информации (особенно по числу наблюдаемых циклов (периодов)), которой часто не хватает.

Следующим недостатком является то, что, выбор мультипликативной модели предполагает непостоянство амплитуды (возрастание или убывание) циклической компоненты в исходных данных, однако в результате расчётов по модели эта амплитуда оказывается неизбежно постоянной. При этом неизбежно увеличение остаточной суммы квадратов отклонений и несоблюдение условий теоремы Гаусса – Маркова в виде гетероскедастичности остатков, что не позволяет использовать метод наименьших квадратов (МНК) для расчёта параметров моделей.

И, наконец, можно отметить, что при достаточном количестве исходных данных последние используются неэффективно, что снижает показатели надёжности моделей и точность прогнозов.

В [9; 10] рассматриваются и более сложные модели, например смешанные аддитивномультипликативные, с использованием гармоник циклической составляющей, с использованием базисов Гребнера [3] и др. Хотя авторы и заявляют, что реализация методов не так сложна, но из-за увеличенного числа идентифицируемых параметров, ужесточаются требования к объёму статистической информации (по мнению авторов [4], на каждый параметр необходимо 6–7 наблюдений), а для построения базисов Гребнера необходимо (для получения достоверных результатов) использовать полиномы высоких степеней и многоразрядные числовые коэффициенты (в примере [8, с. 180–181] рассмотрен полином 20-го порядка с октовигинтиллионной разрядностью коэф- фициентов). Для реализации таких методов нет разработанных пакетов прикладных программ.

В настоящей работе предлагаются существенно более простые методы.

При малом количестве исходных наблюдений рассматривается аддитивная модель (мультипликативную можно привести к ней логарифмированием) и предлагается модель взвешенных тангенсов, анонсированная в [5]. При достаточно большом числе наблюдений (достаточность должна быть обоснована) предложена анонсированная в [6; 7]модель фазовых трендов без выделения циклической компоненты в виде повторяющейся последовательности чисел. При этомпоявляется возможность учёта эволюционного развития циклической компоненты и стирается разница подходов в зависимости от амплитуды периодической составляющей, то есть в разделении моделей на аддитивные и мультипликативные.

Метод взвешенных тангенсов [5]

Для того чтобы не терять исходную информацию на фильтрацию перед выделением циклической компоненты (как это необходимо в описанной выше тренд-сезонной модели), в данной работе предлагается изменить последовательность расчётов и на первое место поставить шаг, бывший ранее под номером 4. Остальные шагиостаются, хотя шаг 2 специфичен, аномерашагов5и6 уменьшаются теперь на 1.

При выполнении предложенной последовательности проблематичным становится шаг 1 (расчёт T ), так как в прошлой методике после устранения S для расчёта T можно было применить метод наименьших квадратов (МНК). При наличии неслучайной составляющей в видециклической компоненты МНК непосредственно не применим, поэтому предлагается альтернативный метод.

Так как метод ранее не применялся, то идею его создания изложим подробно и пока на простейших примерах линейной регрессии (без циклической компоненты). Сначала возникла идея метода средних тангенсов (МСТ). Пусть исходные данные отражены в табл.1, где i – номер наблюдения (точки пространства корреляции).

Таблица 1

Исходные данные для иллюстрации МСТ

Для приведённых данных МНК даст такое уравнение регрессии: у = - 0,5 + 1,4 x + e .

Идея МСТ состоит в том, что каждая линия, соединяющая любые пары точек поля корреляции ( x_i , y_i ) и ( x_j , y_j ) , является в некотором смысле линией регрессии, а тангенс угла а наклона этой линии по отношению к оси абсцисс отражает коэффициент регрессии для этой линии. Так как при объёме выборки, равном n ,

получается

n-1

Z i = i=1

( n - 1) n

линий,   то в

соответствии с МСТ на эту величину и нужно

разделить сумму тангенсов по всем отрезкам, после чего получим средний коэффициент регрессии для всей совокупности исходных данных. В нашем случае tga _{1 - 2} = 1; tga _{1 - 3} = 3/2;

i 1 2 3 4 x 1 2 3 4 y 1 2 4 5 tga1-4 = 4/3; tga2-3 = 2;

^A i - J

tg a _{2 - 4} = 3/2; tg a _{3 - 4} = 1;

( n - 1) n = (4 - 1)4 = 6

2    =    2    =

x , xi

L

(Xj - x. ) n n—1  n

S S ( X j - X i ) i = 1 J = i + 1

n - 1 n

2У yaga,.

^Л М / У 1    ^- j 1 + 3/2 + 4/3 + 2 + 3/2 + 1 25          ⁽³⁾

Ь мст =------------=------------------------ = — ~ 1,39 ,

( n - 1) n                   6                18

а средняя длина L абсциссы отрезков равна n - 1 n

SS ( X j - X . )

L = ‘= ^{1 j} =‘^{+ 1} -------------.

n

где первая сумма отражает перебор первых (левых) точек отрезка, вторая - вторых.

Свободный член можно вычислить по

С учётом (4), а также того, что Iga . j

y j

x j

n

n

-

-

yi

X

• S y bMCT S X‘ формуле aMCT =                =3 =0,48 , n             4

где суммирование проводится по всем значениям соответствующих переменных табл. 1.

Таким образом, МСТ даёт уравнение регрессии y = - 0,48 + 1,39 x + e .

Как видим, МНК и МСТ дают близкие, но всё же различающиеся результаты.

Метод взвешенных тангенсов отличается от МСТ тем, что каждой линии «промежуточной регрессии» и её тангенсу (коэффициенту этой регрессии) присваивается вес, пропорциональный разности абсцисс образующих линию точек. При этом формула (3) преобразуется к виду n - 1 n

формула (3) примет вид

Л bMBT =

n — 1 n

S S ( y j - y . )

г = 1 j = i + 1

n - 1 n

S S (Xj г =1 j = г + 1

—

X . )

.

Л b MBT

² S Z V j tg ^a i - j i = 1 J = i + 1

(3 * )

( n - 1) n

,

где вес A i - j

частичного отрезка определяется

равенством

Применим (5) к данным табл. 1:

_b ^Л = (2 - 1) + (4 - 1) + (5 - 1) + (4 - 2) + (5 - 2) + (5 - 4) ^MBT (2 - 1) + (3 - 1) + (4 - 1) + (3 - 2) + (4 - 2) + (4 - 3)

¹⁴ = 1,4 .

Для расчёта свободного члена применима формула (2), в соответствии с которой получим a _MB t = (12 - 14)/4 = - 0,5.

Полученные по МВТ результаты совпали с результатами по МНК. Случайно ли это? В общем случае да.

Если, например, имеем данные в соответствии с табл. 2, то получим одинаковые уравнения регрессии: у = - 3 + 3 X + e .

Таблица 2

Данные, для которых результаты по МВТ и МНК совпадают

i	1	2	3	4	5
x	1	2	2	3	4
y	1	2	3	5	10

Если же теперь незначимо поменять значения y при неизменных (повторяющихся)

МВТ даст       другое у = -2,66 + 2,86X + e .

уравнение:

значениях x во втором и третьем столбцах (табл. 3), то уравнение регрессии по МНК не изменится, а

Таблица 3

Перестановка второго и третьего столбцов в табл. 2

i	1	3	2	4	5
x	1	2	2	3	4
y	1	3	2	5	10

В следующем разделе покажем, что если наблюдения по факторной переменной равноотстоящие (что характерно для ВР), то методы МНК и МВТ эквивалентны.

МВТ и МНК при равноотстоящих факторах

Как известно, оценка коэффициента регрессии с использованием МНК вычисляется по формуле

_Л      S ( X i ^- X ⁾⁽ у . ^- у )

• ^ьмнк = i=^y     z ,             ⁽⁶⁾

S ( ^х . ^{- x ) 2} i = 1

где X , y - средние значения в наблюдениях фактора и результата.

Обозначим A x = x. _{+ 1} - x. расстояние (шаг) между соседними наблюдениями фактора и будем считать его постоянным. Тогда

- % i + x n    X i + X ] + A x ( n - 1)        A x ( n - 1)

x =     ^    =          2          =X1 +     '’

-                           ,n — 1.A

• X - ^x = ^x + ^{A x (} i ^— 1) ^{— (} x + ^{A x} (     ) = —⁽2 1 ^— n ^— 1).

2      2

Подставим (8) в (6):

b МНК

^{A x}

— £ ⁽² i ^{— n — 1)(} y_t ^— y )

² i = 1

A ²   _П_

A x £ (2 i — n — 1)²

⁴ i = 1

²|_ £ ⁽² i ^{— n —} 1) y i

n

^— y £ ⁽² i ^{— n —} 1) i = 1

A x £ (2 i — n — 1)² i = 1

2£ (2i — n — 1) yi i=1_____________________________ n                                ’

A x £ (2 i — n — 1)²

i = 1

nn

£ (2 i — n — 1) = 2 £ i — n ² — n = 0.

i = 1                               i = 1

Здесь учтено, что

£ i =

i = 1

2 .

n + n

Рассмотрим сейчас коэффициент регрессии для МВТ. Чтобы учесть разницу смысла индексов в (5) и (9), перепишем (5) с другими обозначениями:

n — 1 n

£ £ ( y q — y pi )

;      _ p = 1 q = i + 1 ____________

MBT   n — 1   n

£ £ ( x q — x pi ) p = 1 q = i + 1

где p - номер первой точки частичного отрезка, q - номер второй точки этого отрезка.

Для удобства сравнения (9) и (11) нужно преобразовать двойные суммы в (11) к одинарным. Перепишем пока числитель Ч дроби в правой части (11):

Ч = ^{( y} 2 ^{— y} 1 ) ^{+ (} y 3 ^— y 1 ) ⁺ ( y 4 ^— y 1 ) ⁺ •• ^{+ (} y n — 2 ^— y 1 ) ^{+ (} y n — 1 ^— y 1 ) ^{+ ( y}n ^— y 1 ) ⁺

^{+ (} y 3 ^— y 2 ) ^{+ (} y 4 ^— y 2 ) ⁺ • ” ^{+ (} y n — 2 ^— y 2 ) ⁺

⁽ y n — 1 ^— y 2 ) ^{+ (} y n ^— y 2 ) ⁺

^{+ (} y 4 ^— y 3 ) ⁺ • ^{+ (} y n — 2 ^— y з ) ^{+ (} y n — 1 ^— y з ) ^{+ (} y n ^— y з ) ⁺

^{+ (} y n — 2 ^— y n — 3 ) ^{+ (} y n — 1 ^— y n — 3 ) ⁺ ( y n ^— y n — 3 ) ⁺

^{+ (} y n — 1 ^{— y}n — 2 ) ^{+ ( y}n ^{— y}n — 2 ) ⁺

^{+ (} y n ^{— y}n — 1 ) . Для удобства группировок все элементы со знаком «минус» просуммируем по строкам, а со знаком «плюс» - по столбцам, тогда

Ч = ( n ^— DC — ^y 1 ) + ( n ^{— 2})( — ^y 2 ) ⁺ ( n ^{— 3})( — ^y 3 ) ⁺ ...

+ 3( — y n — 3 ) + 2( — y n _ ₂) + 1( — y n . , ) +                              (12)

^{+ y} 2 ^{+ 2 y} 3 ⁺ ... ^{+ ( n — 4)} У „ — 3 ^{+ ( n — 3)} y n — 2 ⁺

^{( n — 2)} y n — 1 ^{+ ( n —} 1) y n =

(1 — n ) y + (3 — n ) y ₂ + (5 — n ) y ₃ + ...

n

^{( n — 5)} y n — 2 ^{+ ( n — 3)} y n — 1 ^{+ ( n —} 1) y n = £ ⁽² i ^{— n —} 1) y, .

i = 1

Аналогичные действия со знаменателем

З дроби в правой части (11) дают

n

З = £ (2 i — n — 1) x , . С учётом (10) можно i = 1

записать

nn    n

З = £ (2 i — n — 1)( x , — x ) = £ (2 i — n — 1)(-(2 i — n — 1)    „£ (2 i — n — 1)².

i = 1                                             1 = 1                          ^{2                               2} i = 1

Деление Ч на З позволяет сделать вывод, ^{что Ь} мнк = ^Ь мвт .

Так как свободный член для МНК и МВТ можно вычислить по одной и той же формуле (2), то при равноотстоящих значениях факторы МНК и МВТ эквивалентны.

Применение МВТ для анализа ВР

Данные ВР обычно наблюдаются через равные дискреты времени, что должно обеспечить применимость МВТ и его эффективность (минимум остаточной суммы квадратов по «наследству» от МНК в силу эквивалентности) при выделении тренда. Обычно заранее известна периодичность циклической составляющей в виде числа циклов (периодов) и числа наблюдений на один цикл (в экономических исследованиях это чаще всего 4 квартала или 12 месяцев).

Пусть наблюдения каждого периода циклической компоненты пронумерованы от t = 1 до t = k s ( k_s - количество наблюдений за 1 цикл). С учетом этого можно определить время для всего ВР:

p = 1, S p ; c = 1, s_c ; t = p + c ( S p — 1).

При наличии S-компоненты (циклической) для непосредственного выделения тренда можно использовать соответствующие точки t разных циклов. Тогда линии, соединяющие эти точки, будут частными линиями регрессии (трендов), а совокупность частных коэффициентов регрессии позволит найти общий коэффициент регрессии тренда ВР, например по МСТ, но лучше по МВТ. В последнем случае формулу (11) можно преобразовать к виду k s k_c — 1 k_c £ £ £ ( y q — y pi ) h — t = 1 p = 1 q = i ^{+ 1} b MBT =       k S    k c             ,           (14)

k s £  £ ( q — p )

p = 1 q = i + 1

где k_c - количество циклов временного ряда;

p - номер цикла (периода ВР), в котором находится первая (левая по траектории) из точек с номером t отрезка частного тренда;

• q - номер цикла для второй точки отрезка;

первый индекс в массиве y уровней ВР означает принадлежность к циклу, второй – номер точки внутри цикла.

Свободный член можно вычислить по формуле k c k s            ˆ

E E ( y n_c , t - b MBT ( t ⁺ k s ( ⁿ c - ¹⁾⁾⁾

a MBT = n c ^ ^t ^ ¹ ------^------------  ,   (15)

kc ■ ks где nc = 1, kc - номер цикла.

Зная уравнение тренда T = а + bt, можно выделить сумму циклической компоненты с остатками S + E = у — T, но так как значения E случайны и не повторяются из цикла в цикл, то для получения повторяющихся последовательностей значений S нужно каждую её точку t усреднить по всем циклам:

kc

E ( S n c , t + E n c , t )    _

S (t ) = n c =-----;----------, t = 1, k_s .                 (16)

kc

Для сравнения приведём основные результаты расчётов для известного [4, с. 311-317] примера.

Исходные данные для примера приведены в табл. 4.

Таблица 4

Потребление электроэнергии жителями Северо-Западного региона за 16 кварталов 2003–06 гг. (млн кВт/ч, [4])

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
y	6	4,4	5	9	7,2	4,8	6	10	8	5,6	6,4	11	9	6,6	7	10,8

Здесь i – это номер наблюдения, имеющий смысл «сквозного» (в пределах всего ВР, а не только одного цикла) дискретного времени. Предварительный анализ данных показывает, что данный ВР содержит возрастающий тренд, который будем считать линейным, а также циклическую компоненту, содержащую kс =4 периода по ks =4 наблюдения в каждом.

Результаты для сравнения приведены в табл. 5. Данные табл. 4 и результатов расчета табл. 5 приведены на рис. 1.

Таблица 5

Результаты расчета по модели (1) и МВТ

i	S	T=5,715+ 0,186i	E	Å 2	T =5,813+0,175i MBT	MBT	MBT	2 MBT
1	0,518	5,901	-0,483	0,2333	5,9875	0,5125	-0,5	0,2500
2	-1,977	6,088	0,289	0,0835	6,1625	-1,8625	0,1	0,0100
3	-1,294	6,275	0,019	0,0004	6,3375	-1,2875	-0,05	0,0025
4	2,690	6,461	-0,151	0,0228	6,5125	2,6375	-0,15	0,0225
5		6,648	-0,029	0,0008	6,6875		0	0
6		6,834	-0,057	0,0032	6,8625		-0,2	0,0400
7		7,020	0,273	0,0745	7,0375		0,25	0,0625
8		7,207	0,104	0,0108	7,2125		0,15	0,0225
9		7,393	0,026	0,0007	7,3875		0,1	0,0100
10		7,580	-0,030	0,0009	7,5625		-0,1	0,0100
11		7,766	-0,072	0,0052	7,7375		-0,05	0,0025
12		7,952	0,358	0,1282	7,9125		0,45	0,2025
13		8,139	0,280	0,0784	8,0875		0,4	0,1600
14		8,325	0,252	0,0635	8,2625		0,2	0,0400
15		8,519	-0,218	0,0475	8,4375		-0,15	0,0225
16		8,698	-0,588	0,3457	8,6125		-0,45	0,2025
E	0	116,8	0	1,0994	116,8	0	0	1,0600

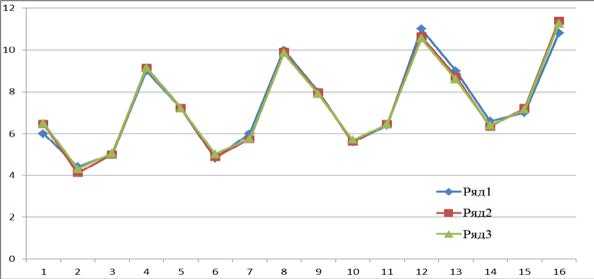
Рис. 1. Траектории временного ряда для примера [4]: ряд 1 – исходные данные, ряд 2 – расчет по модели (1), ряд 3 – расчет по МВТ

Некоторые выводы:

• 1.    Несмотря на то что результаты расчётов по известному и предложенному методам эквивалентны (предложенный всё же чуть эффективнее, и остаточная сумма квадратов уменьшилась на величину, превышающую возможную сумму погрешностей округлений), применимость метода можно считать обоснованной.

• 2.    К достоинству нового метода можно отнести то, что он не так требователен к объёму исходных данных. При использовании в известном методе фильтрации методом скользящей средней информация о циклической компоненте требует как минимум одного дополнительного цикла, информации о котором может вообще не быть.

• 3.    Оба метода предполагают неизменность циклической и трендовой компонент во времени, что не всегда соответствует наблюдаемым данным.

Предложенный метод может обойтись одним циклом предшествующей статистики, что и было использовано для прогнозирования деятельности малого предприятия, имеющего предысторию в один год. Других методов с таким сроком просто не существовало.

Для устранения последнего недостатка можно применить предлагаемый ниже метод фазовых трендов.

Метод фазовых трендов (МФТ) [6; 7]

Метод не предполагает выделение в явном виде циклической компоненты, но может быть применён лишь после её обнаружения. Факт наличия может быть обнаружен в траектории ВР, в периодограмме или спектрограмме анализа Фурье, а также в автокорреляционной функции наблюдаемого ВР.

Предполагается, что ВР содержит несколько ( k_c ) циклов (периодов), а в каждом цикле имеется несколько ( k_s ) равноотстоящих наблюдений, как это и было в предыдущем примере ( k c = 4; k s = 4 ). Каждое наблюдение внутри цикла имеет номер t = 1, k s . Каждое значение t отражает фазу внутри цикла. Одинаковые фазы разных циклов предполагаются коррелированными, причём для каждой фазы может быть найдено своё уравнение регрессии.

Т.к. предлагаемый метод прост, его реализацию рассмотрим сразу на числовом примере (том же). Пока выделим из данных табл.4 первую фазу (табл. 6).

Таблица 6

Данные п о первой фазе числовог о примера

i	1	5	9	13
yi	6	7,2	8	9

Если принять тренд линейным

Tj = a 1 + b1 i, то МНК (и МВТ тоже) даст уравнение T1 = 5,835 + 0,245i, где i - дискретное время в сквозной нумерации (не внутри цикла). Остаточная сумма квадратов Sp  для этого уравнения составила 0,028.

Эти результаты и результаты для других фазовых трендов сведены в табл. 7.

Таблица 7

Результаты расчета по методу МФТ

T 1 = 5,835 + 0,245 i			T 2 = 3,870 + 0,185 i			T 3 = 4,660 + 0,160 i			T 4 = 8,600 + 0,160 i
S p =0,028			S p =0,092			S p =0,072			S p =0,432
i	yi	T i	i	yi	T i	i	yi	T i	i	yi	T i
1	6	6,08	2	4,4	4,24	3	5,0	5,14	4	9,0	9,24
5	7,2	7,06	6	4,8	4,98	7	6,0	5,78	8	10,0	9,88
9	8	8,04	10	5,6	5,72	11	6,4	6,42	12	11,0	10,52
13	9	9,02	14	6,6	6,46	15	7,0	7,06	16	10,8	11,16

Можно заметить, что остаточная сумма квадратов для модели в целом S _z =0,028+0,092+0,072+0,432=0,624 заметно меньше, чем для случая общего тренда и постоянной сезонной компоненты (1,099 из табл. 5), улучшатся также и другие характеристики надёжности – наблюдаемые значения коэффициентов детерминации, Тейла, критерия Фишера, средней ошибки аппроксимации.

Естественно, что МФТ можно использовать не только с линейными трендами.

Например, если все тренды выбрать в виде показательных функций, то остаточная сумма квадратов для этого примера несколько уменьшится. В принципе для трендов разных фаз можно использовать разные функции, например, для первой фазы линейную, для второй – показательную и т. д.

Примеры реализации МФТ на реальных данных

Можно, конечно, привести множество специально подобранных примеров, где лучшим будет предлагаемый разработчиками метод.

Поэтому для сравнения мы решили использовать результаты уже опубликованных методов (и с теми же данными), которые разработчики считают лучшими. Кроме того, мы рассматривали реальные данные в тех же временных интервалах, что и у разработчиков для того, чтобы можно было сравнить результаты по характеристикам, выбранным разработчиками.

В табл. 8 приведен пример индекса реального ВВП по данным Росстата.

Таблица 8

Данные индекса реального ВВП

Год	2003				2004				2005
Квартал	1	2	3	4	1	2	3	4	1	2	3	4
Индекс	100	106,9	121,4	120,7	107,0	115,2	130,2	128,7	112,8	122,3	138,3	138,4
МФТ	98	105,2	119,1	122,4	106,7	114,8	129,2	131,0	115,2	124,3	139,4	139,6
Год	2006				2007				2008
Квартал	1	2	3	4	1	2	3	4	1	2	3	4
Индекс	120,2	131,7	138,3	138,4	129,3	142,2	160,5	163,6	140,5	153	170,2	165,5
МФТ	123,7	133,9	149,6	148,1	132,2	143,5	159,7	156,7	140,6	153	169,9	165,2

На рис. 2 приведены траектории временного ряда по индексу реального ВВП РФ на основе данных, представленных в табл. 8.

Построенная по этим данным ARMA-модель [9; 10] с использованием базиса Гребнера [3; 12] предполагала использование полиномиального уравнения 20-го порядка и 80-разрядных коэффициентов (чтобы не потерять точность). К сожалению, авторы не привели поквартальные данные по этой модели. Отмечено, что коэффициент детерминации составил

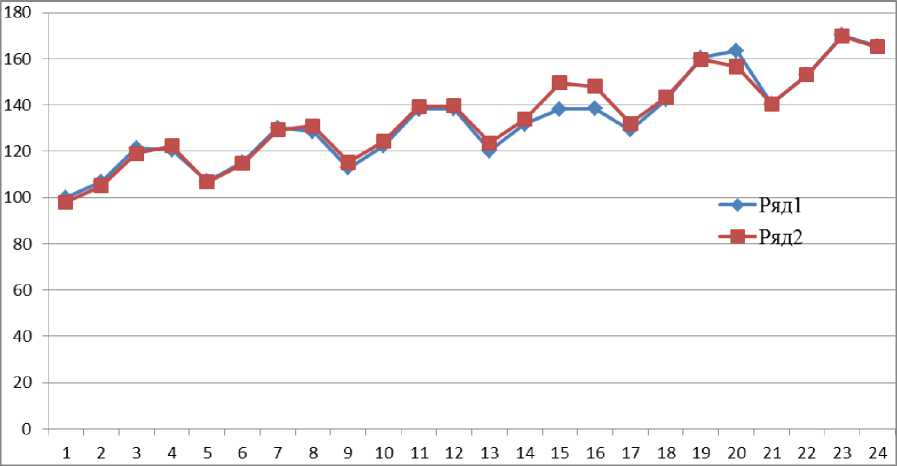
Рис. 2. Траектории временных рядов индекса ВВП РФ: ряд 1 – исходные данные [11], ряд 2 – расчет по МФТ

По методу фазовых трендов получено r2 = 0,9999; MAPE = 1,93% .            Эти характеристики не хуже, чем у авторов в [9]. При этом фазовые тренды были выбраны линейными, и после расчётов приняли вид

T = 96,087 + 2,12129 1 ; T ₂ = 100,397 +

+ 2,392929 1 ; T ₃ = 111,455 + 2,5405 1 ;

T ₄ = 113,887 + 2,139357 1 .

R 2 = 0,99 , а оценка

MAPE = 1 nr | (yk ~ yk )  | = 2,74%, что l k=n+1        yk подтверждает высокую точность моделирования и прогнозирования. Здесь n=12  – количество кварталов, по которым строилась модель (обучающая выборка), l=8 – количество кварталов, по которым сравнивались реальные и прогнозные данные (контролирующая выборка).

Здесь номер фазы совпадает с номером квартала.

Для иллюстрации применения нелинейных трендов мы взяли (у тех же авторов) поквартальную информацию об объёме инвестиций в основной капитал Самарской области за 9 лет (табл. 9).

Таблица 9

Инвестиции в основной капитал Самарской области

Год	2000				2001				2002
Квартал	1	2	3	4	1	2	3	4	1	2	3	4
Инвестиции	5768	10086	24855	22871	5898	4314	21407	24336	7020	4013	22369	26479
Модель Авторов[8]	3856	13560	28723	18601	1549	5044	25139	23720	5084	3557	22539	27422
МФТ	6439	7142	23202	25404	5837	6482	21569	22353	6672	6899	23532	24277
Год	2003				2004				2005
Квартал	1	2	3	4	1	2	3	4	1	2	3	4
Инвестиции	9486	7625	27267	31512	13622	12408	36341	42283	18468	16188	51061	59461
Модель Авторов [8]	10574	8223	24735	31290	15033	16575	34104	38752	18027	23671	50405	53516
МФТ	8944	8395	29089	31182	12652	10970	38240	43065	17796	14622	50986	59927
Год	2006				2007				2008
Квартал	1	2	3	4	1	2	3	4	1	2	3	4
Инвестиции	22807	20108	71071	80768	29570	25989	91039	10661 8	44885	30340	106568	142614
Модель Авторов [8]	22532	25313	70132	78101	33658	20410	86871	11266 2	56869	12626	93118	154037
МФТ	24378	19352	67327	81767	32396	25161	87262	10858 6	37110	35372	119013	136041

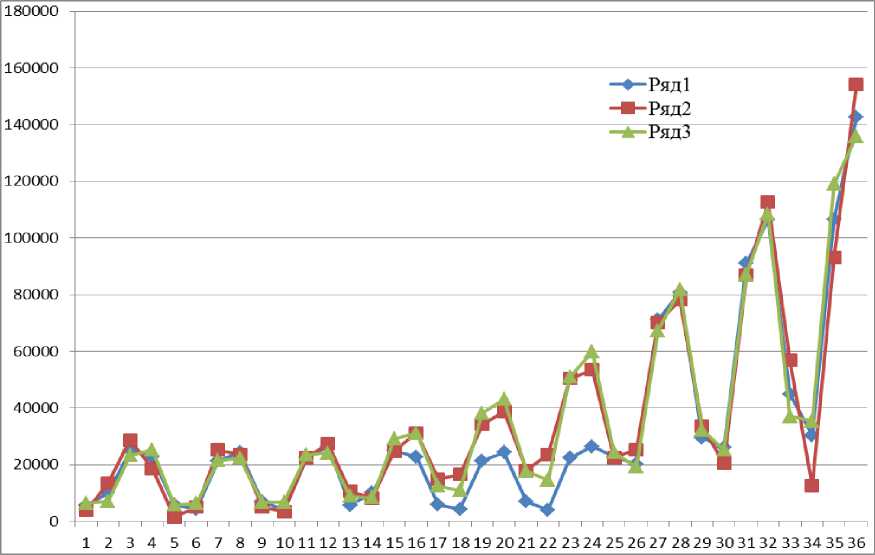
Рис. 3. Траектории временных рядов: ряд 1 – данные наблюдений [9], ряд 2 – расчет по модели [9], ряд 3 – расчет по МФТ

На рис. 3 приведены графики временных рядов по данным, представленными в табл. 9.

Здесь в авторском варианте [9] использовалась мультипликативно-аддитивная модель, в которой тренд был представлен полиномом второго порядка, циклическая компонента в мультипликативной части содержала 2 гармоники, а аддитивная часть также содержала гармонику:

y_k = ( D 1 ( k A)² + D 2 k A + D 3 ) х (1 + A 1 sin( ® k A) +

+ 6 B 1 cos(ok A) + A 2 sin(2 m k A) + B 2 cos(2 m k A)) +

E 1 sin( m k A) + F 1 cos( m k A).

Качество модели и прогнозов характеризуют следующие показатели:

R ² = 0,9828, MAPE = 26% .

По виду траектории для МФТ мы выбрали тренды в виде парабол 2-го порядка: T = a + bx + cx ² .

В         результате         получили:

T 1 = 6814,1 - 419,80 1 + 44,894 1 ² ;

T₂ = 7876,3 - 434,60 1 + 33,692 1 ²;

T ₃ = 26785,0 - 1531,41 1 + 112,332 1 ²; T ₄ = 33434,7 - 2630,06 1 + + 155,579 1 ².

При этом

R ² = 0,9987; MAPE = 1,15% .

В табл. 9 за 2008 г. модельные данные приведены по прогнозам моделей, построенных по данным до 2008 г. Реальные данные за 2008 г. использованы как контролирующая выборка.

По графикам рис. 3 видим, что МФТ в этих примерах даёт результаты не хуже, чем существенно более сложные модели [9]. Отметим, что на рис. 3 используется сквозная нумерация кварталов за 2000–2008 гг.

Выводы

В работе предложены два простых метода построения моделей временных рядов – метод взвешенных тангенсов и метод фазовых трендов. К основным достоинствам первого метода можно отнести то, что он позволяет построить модель при меньшем объёме статистической информации, чем для существующих методов. Основными достоинствами второго метода являются простота, возможность учёта эволюции циклической компоненты временного ряда, хорошие характеристики надёжности.