К вопросу о применимости производственных функций для системного анализа реальной экономики

TO THE ISSUE OF APPLICABILITY OF PRODUCTION FUNCTIONS TO THE PRODUCTIVE ECONOMY SYSTEM ANALYSIS

Lebedev Valerij1, Lebedev Konstantin2,

Mikhailov Aleksandr3

1Doctor of Economics, Candidate of Physics and Mathematics, Professor, Academician of RANS, head of mathematics chair;

State University of Management, mathematics chair;

109542, Moscow, Ryazansky avenue 99;

Dubna International University of Nature, Society and Human,

Institute of system analysis and management;

2Candidate of Economics,

Federal state budget scientific institution «Scientific-Research Institute – Republican Research Scien-tific Consultative Centre of Inspection»; director of Centre of research and statistics of science;

123995, Moscow Antonov-Ovsienko street, 13, building 1;

3Post-graduate student;

State University of Management, mathematics chair;

109542, Moscow, Ryazansky avenue 99;

Формализованное описание производственных процессов относится к ключевым вопросам экономической науки. Существенное место в этом направлении исследований занимают производственные функции. Более восьмидесяти лет назад в работе [9] была построена производственная функция:

1 3

P = 1,01 C ⁴ L ⁴,

которая отражала связь между физическим объемом производства P и основными факторами производственного сектора США ( C - капитал (основные производственные фонды), L – численность занятых в производстве).

После публикации работы [9] производственная функция вида: Y = AK ^a L ^e e ^Y ,

где K – основные производственные фонды (капитал), L – численность занятых в производстве, а , в , / и A — параметры (фиксированные числа), стала быстро распространяться в научной экономической литературе. В настоящее время производственная функция стандартного вида (2), получившая название производственной функции Кобба–Дугласа, широко используется для теоретического анализа различных механизмов экономического развития. В частности, она применяется при анализе производственных процессов в микроэкономической модели 2×2×2, при анализе макроэкономической динамики в модели Солоу [1-5].

Наибольшее распространение получила линейно-однородная производственная функция вида:

Y = AK ^a L^{1 —а} ,

которая является частным случаем функции (2) при в = 1 — а , у = 0 . Отметим, что именно такая функция была построена в работе [9].

К сожалению, при анализе практических задач управления производственные функции вида (2) часто применяется формально, без анализа вопросов адекватного описания реальных процессов. Одним из примеров некорректного подхода к построению производственных функций вида (2) является оценка ее параметров на основе размерных статистических данных. Такой формальный подход связан, по-видимому, с тем, что в работе [9] авторы не акцентировали внимание читателей на технической методике построения уравнения (1), вследствие чего процедура обезразмеривания переменных, выполненная ими, не является очевидной.

В качестве исходных данных Ч. Кобб и П. Дуглас использовали статистические данные, характеризующие динамику физического объема производства, основных производственных фондов (капитала) и численности занятых в производстве. При этом основные фонды измерялись в млн. долларов США в ценах 1880 г., численность занятых в производстве – в тыс. человек, а изменение конечного продукта характеризовалось безразмерным индексом Дэя–Персонса [10]. Использованные в работе [9] исходные статистические данные приводятся в столбцах (3), (4) и (5) таблицы 1.

Таблица 1. Динамика показателей производства (рассчитана по данным работы [9])

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
t	Год	K t	L t	Y t	u t	v t	x t	y t	λ t
0	1899	4 449	4 713	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000
1	1900	4 746	4 968	1,0099	1,0668	1,0541	1,0120	0,9581	0,9467
2	1901	5 061	5 184	1,1192	1,1376	1,0999	1,0342	1,0175	0,9839
3	1902	5 444	5 554	1,2202	1,2236	1,1784	1,0384	1,0354	0,9972
4	1903	5 806	5 784	1,2401	1,3050	1,2272	1,0634	1,0104	0,9502
5	1904	6 132	5 468	1,2202	1,3783	1,1602	1,1880	1,0517	0,8853
6	1905	6 626	5 906	1,4305	1,4893	1,2531	1,1885	1,1415	0,9605
7	1906	7 237	6 251	1,5199	1,6267	1,3263	1,2264	1,1459	0,9343
8	1907	7 832	6 483	1,5099	1,7604	1,3756	1,2798	1,0977	0,8577
9	1908	8 229	5 714	1,2599	1,8496	1,2124	1,5256	1,0392	0,6812
10	1909	8 820	6 615	1,5497	1,9825	1,4036	1,4125	1,1041	0,7817
11	1910	9 240	6 807	1,5894	2,0769	1,4443	1,4380	1,1005	0,7653
12	1911	9 624	6 855	1,5298	2,1632	1,4545	1,4872	1,0518	0,7072
13	1912	10 067	7 167	1,7699	2,2628	1,5207	1,4880	1,1639	0,7822
14	1913	10 520	7 277	1,8394	2,3646	1,5440	1,5314	1,1913	0,7779
15	1914	10 873	7 026	1,6904	2,4439	1,4908	1,6394	1,1339	0,6917
16	1915	11 840	7 269	1,8891	2,6613	1,5423	1,7255	1,2248	0,7098
17	1916	13 242	8 601	2,2517	2,9764	1,8250	1,6309	1,2338	0,7565
18	1917	14 915	9 218	2,2699	3,3524	1,9559	1,7140	1,1605	0,6771
19	1918	16 265	9 446	2,2318	3,6559	2,0042	1,8241	1,1135	0,6105
20	1919	17 234	9 096	2,1805	3,8737	1,9300	2,0071	1,1298	0,5629
21	1920	18 118	9 110	2,3129	4,0724	1,9330	2,1068	1,1966	0,5680
22	1921	18 542	6 947	1,7897	4,1677	1,4740	2,8274	1,2142	0,4294
23	1922	19 192	7 602	2,3692	4,3138	1,6130	2,6744	1,4688	0,5492

Несмотря на то, что авторы работе [9] не утомляют читателей математическими выкладками, фактически они использовали безразмерные переменные при построении уравнения (1). Введем KL безразмерные величины и = — и v = — ; соответствующие расчетные значения приведены в t  Kо     t L столбцах (6) и (7) таблицы 1 соответственно. На основании динамических рядов безразмерных величин {ut}, {vt} и {Yt}, где t = 0,1, ...,23, в работе [9] с помощью стандартных эконометрических методов была решена задача определения параметров A и α функции двух переменных:

Y = Au ^a v ¹-^а .

Ч.Коббом и П.Дугласом были получены конкретно следующие значения параметров производственной функции (4): A = 1,01, а = 0,25 [9].

Введем следующие переменные: фондовооруженность труда x = K / L и производительность труда y = Y / L. Если для описания производственных процессов использовать производственную функцию (2), то для производительности труда получаем:

y = Ax“L“+в-1 eY.

Как видим, здесь производительность труда зависит в общем случае от трех переменных: x , L и t . Если же использовать производственную функцию вида (3), то для производительности труда получаем:

У = Axa,

т.к. в этом случае а + в = 1 , у = 0, и, следовательно, производительность труда зависит здесь только от одной переменной x .

В дальнейшем мы будем предполагать, что производительность труда зависит только от фондовооруженности труда. Соответствующую многопараметрическую зависимость y = f (x, h X                                      (7)

где h — вектор параметров, будем называть производственной зависимостью. Отметим, что функция (6) является одним из частных случаев производственной зависимости (7).

Используем статистические данные работы [9] для построения производственных зависимостей. Для этого вычислим значения фондовооруженности труда x = K / L и производительности труда y_t = Y / L при t = 0,1,.. .,23 ; эти значения приведены в столбцах (8) и (9) таблицы 1. На рис. 1 в плоскости «фондовооруженность труда – производительность труда» соответствующие точки ( x_t ; y_t ) отмечены ромбами.

Для аппроксимации производственной зависимости можно использовать различные многопараметрические функции y = f (x, h ) . При этом для определения значений параметров можно использовать различные критерии аппроксимации. В данной работе мы определяли значения параметров производственных зависимостей из решения задачи о минимизации среднего относительного отклонения:

F ( h ) =

N + 1

N t=0

f( xt, h ) - yt yt

X 100%.

Рассмотрим несколько вариантов построения производственной зависимости.

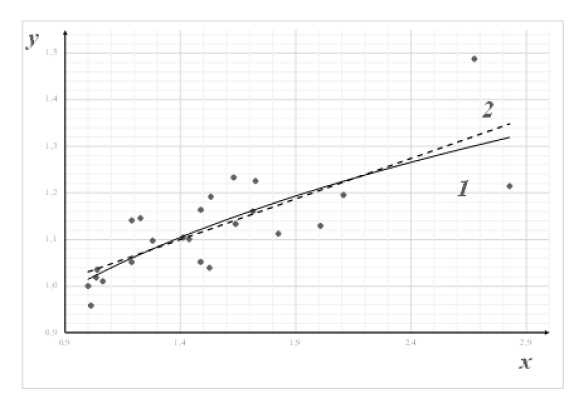
Рис. 1. Аппроксимация производственной зависимости степенной (1) и линейной (2) функциями

При аппроксимации производственной зависимости степенной функцией вида f (x, h) = Axa нами получено h* = {1,0103; 0,2335}. При этом значение минимального среднего относительного отклонения равно F (h* ) = 4,07%. Из полученной производственной зависимости y = 1,0103 x °’2335

формально следует уравнение производственной функции Y = 1,0103 K ^0,2335 L ⁰’⁷⁶⁶⁵. Как видим, полученный здесь результат соответствует результату работы [9] (незначительные различия параметров связаны с использованием разных критериев близости).

К каким результатам приводит использование других функций для аппроксимации теоретической зависимости (7)? В случае линейной аппроксимации функцией у = ax + b минимуму среднего относительного отклонения F ( h ), где h = { a ; b } , будет соответствовать зависимость

у = 0,1677x + 0,8593.

При этом значение среднего относительного отклонения будет равным F ( h ₂*) = 4,35%. Как видим, значения среднего относительного отклонения в обоих случаях различаются мало.

Рассмотрим случаи приближения производственной зависимости (7) полиномами второй, третьей и четвертой степеней. Минимизируя в этих случаях среднее относительное отклонение F ( h ), мы получим соответственно уравнения:

у = -0,0347x2 + 0,2966x + 0,7568, у = 0,0525x3 - 0,3246x2 + 0,7954x+0,4886, у = -0,7681x4 + 5,700x3 -15,2692x2 +17,6543x - 6,3459.

4,31%,

При этом соответствующие значения среднего относительного отклонения равны

4,20% и 3,98%. Таким образом, значения среднего относительного отклонения при аппроксимации

3,000

2^0°                                                        (1)/

0,500

одю

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Рис. 2. Динамика фондовооруженности (1) и производительности труда (2)

производственной зависимости полиномами первой, второй и третьей степени выше, чем значение среднего относительного отклонения при аппроксимации степенной функцией. И только при аппроксимации полиномом четвертой степени значение среднего относительного отклонения ниже, чем при аппроксимации степенной функцией вида (6). Как видим, во всех рассмотренных случаях значения среднего относительного отклонения отличаются мало (лежат на уровне четырех процентов) и поэтому вряд ли можно говорить о том, что степенная функция вида (6) наилучшим образом отражает статистические данные работы [9]. Тем не менее, степенная функция вида (6) имеет преимущество перед другими рассмотренными способами аппроксимации производственной зависимости (7): эта функция позволяет определить значение среднего на рассматриваемом промежутке времени коэффициента эластичности.

Наряду с коэффициентом эластичности производственной зависимости к дифференциальным характеристикам рассматриваемых процессов относятся темпы прироста фондовооруженности труда и производительности труда. Эти характеристики взаимосвязаны. Действительно, предположим, что фондовооруженность труда и производительность труда растут с постоянными темпами прироста у и 6 соответственно: x = x_oe ^Y , у = у_ов ⁶ . Тогда формально фондовооруженность труда и производительность труда связаны соотношением:

у = у 0

и, таким образом, коэффициент эластичности производственной зависимости равен отношению темпов прироста производительности труда и фондовооруженности труда.

Выполненная нами аппроксимация динамики фондовооруженности труда и производительности труда экспоненциальными функциями с использованием статистических данных работы [9] (соответствующие динамические ряды приведены в (8) и (9) столбцах таблицы 1) дала следующие результаты: темп прироста фондовооруженности у = 3,64%, а темп прироста производительности труда 0 = 0,88%. Поэтому среднее значение коэффициента эластичности производственной зависимости в период 1899 - 1922 гг. равно 0 / у = 0,242. Этот результат соответствует полученной выше формуле (8) и результату, приведенному в работе [9].

Статистические данные работы [9] отражают неравномерность развития производственного сектора американской экономики в период 1899 – 1922 гг. Для обоснования этого вывода зависимости от времени фондовооруженности труда x = X(t) и производительности труда y = Y(t) аппроксимировались непрерывными функциями с конечно постоянными темпами прироста. Согласно выполненным нами расчетам установлено, что можно выделить четыре периода с различными дифференциальными характеристиками развития производственного сектора СЩА: 1899 - 1910 гг., 1910 - 1916 гг., 1916 - 1920 гг. и 1920 - 1923 гг. В эти периоды времени фондовооруженность труда росла в среднем с темпами прироста 3,91%, 1,97%, 6,14% и 11,62%, а производительность труда изменялась в среднем с темпами прироста 0,93%, 1,57%, -3,82% и 8,9% соответственно. (Отметим, что отрицательное значение темпа прироста сглаженной производительности труда в третьем периоде отражает падение значений производительности труда в период 1917 - 1919 гг., приведенных в таблице 1). Поэтому коэффициент эластичности производственной зависимости y = f (x) , построенной на основании статистических данных работы [9], не является постоянным: с 1899 по 1910 гг. он был равен 0,24; с 1910 по 1916 гг. был равен 0,8; с 1916 по 1920 гг. был отрицательным (–0,62); с 1920 по 1922 гг. был равен 0,77.

Рис. 2 служит иллюстрацией выполненных расчетов. Здесь построены точки ( t ; x_t ) и ( t ; y_t ) , где t = 1, 2,..., 24, которые соответствуют значениям фондовооруженности труда и производительности труда таблицы 1, и графики функций с кусочно-постоянными темпами изменения x = X ( t ) и y = Y ( t ) , которые являются результатом аппроксимаций зависимостей от времени фондовооруженности труда и производительности труда (линии (1) и (2) соответственно).

Выводы

• 1.    Производственная функция Кобба–Дугласа, построенная в работе [9], относится к фундаментальным понятиям экономической науки. Она широко используется для теоретического анализа механизмов развития различных экономических процессов. Однако применение производственной функции Кобба–Дугласа и ее модификаций для выполнения реальных прогнозных оценок часто оказывается неэффективным. Это связано, прежде всего, с тем, что реальные статистические данные не позволяют построить производственные зависимости с постоянными значениями параметров и удовлетворительными статистическими характеристиками.

• 2.    Коэффициент эластичности построенной в работе [9] производственной функции отражает отношение значений среднего темпа прироста производительности труда и среднего темпа прироста фондовооруженности труда в период 1899-1923 гг. Выполненный анализ статистических данных работы [9] свидетельствует о том, что производственный сектор американской экономики в период с 1899 по 1922 гг. развивался неравномерно, вследствие чего коэффициент эластичности теоретической зависимости производительности труда от фондовооруженности труда был существенно непостоянным.

Для выполнения конкретных макроэкономических исследований на перспективу представляется целесообразным использовать подход, опирающийся на прогнозирование динамики коэффициента фондоотдачи с применением сплайн-анализа данных базового периода. При этом могут быть использованы как линейные сплайны (с кусочно-постоянной скоростью изменения), так и нелинейные сплайны (с кусочно-постоянным темпом изменения, с кусочно-постоянной эластичностью и др.) [6 – 8]. Преимущество такого подхода определяется, на наш взгляд, тем, что прогнозирование вариантов динамики коэффициента эластичности – технически более сложная задача, чем прогнозирование динамики коэффициента фондоотдачи. 1 Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 13-06-00389).