К вопросу о рациональном распределении инвестиций в проекты регионального развития

При принятии многокритериальных решений на всех уровнях неизбежна проблема конфликта интересов, которая объективно возникает в ситуации выбора. В задаче распределения инвестиций в региональные инвестиционные проекты сущность рассогласования интересов можно представить как противоречие между социальной и экономической эффективностью. Необходимо отметить, что социальный и экономический аспекты принятия инвестиционных решений дополняют друг друга и являются взаимозависимыми. Основной вопрос заключается в том, какой тип корреляции наблюдается между ними и какова теснота корреляционной связи. Лицо, принимающее решение, может выбирать в качестве приоритета либо экономическое факторы, игнорируя социальные интересы, либо делать акцент на социальном развитии, ограничивая возможности получения экономической отдачи. Целесообразным является нахождение баланса между двумя крайними позициями. Основная задача органов государственного управления заключается в достижении синергетического эффекта при одновременном наращивании экономического и социального потенциала. Следовательно, для принятия решений при распределении инвестиций в региональные проекты необходим инструментарий, позволяющий сбалансировать интересы сторон и минимизировать уровень рассогласования.

Цель данной работы – усовершенствовать методический инструментарий распределения инвестиций в региональные инвестиционные проекты с учетом интересов стейкхолдеров.

В процессе достижения поставленной цели предполагается последовательно решить следующие задачи:

– выявить факторы, которые необходимо учитывать при оценке региональных инвестиционных проектов;

– определить структуру и связи механизма оценки экономических и социальных факторов эффективности региональных инвестиционных проектов;

– сформировать интегральные критерии экономической и социальной эффективности проектов;

– определить уровень дисбаланса между критериями экономической и социальной эффективности;

– предложить механизм распределения инвестиций в региональные инвестиционные проекты на основе минимизации общего уровня дисбаланса интересов стейкхолдеров.

В отечественной литературе широко представлены подходы к отбору проектов [1–3]. При этом в одних работах акцент делается на развитие инструментария и применение математического аппарата [4–6], а в других – на организационных аспектах и конкретизации критериев оценки [7–9].

В зарубежной литературе вопросы, связанные с отбором проектов рассмотрены в работах К. Chatterjee, S.A. Hossain, S. Kar [10], Ch. Huang, P. Chu, Y. Chiang [11], S.A. Gabriel, S. Kumar, J. Ordonez, A. Nasserian [12] и других авторов. Данные подходы основаны на применении метода анализа иерархий (МАИ), предложенного Томасом Саати [13]. При этом в работах [11, 12] метод Саати ис- пользуется в комбинации с другими методами (теория нечетких множеств, метод Монте-Карло).

М.С. Кувшинов и Н.С. Комарова отмечают, что многообразие методических подходов к отбору проектов объясняется индивидуальными характеристиками самих проектов и вариативностью их результатов [14]. Следовательно, актуальной является проблема выбора методического инструментария, корректного для достаточно широкого множества проектов.

Методы

Для формирования интегральных социального и экономического критериев оценки региональных инвестиционных проектов предлагается использовать модифицированный метод анализа иерархий (ММАИ), описанный в работе T.J. Kim [15].

Традиционный метод анализа иерархий позволяет формализовать процедуру экспертной оценки и предполагает попарное сравнение альтернатив, при котором эксперт выносит n(n–1)/2 суждений. С этой целью строится квадратная матрица размерностью n×n, в которую заносятся результаты оценки. Матрица является симметричной относительно диагонали. В качестве требуемых условий для корректной оценки необходимо отметить соблюдение кардинальности и транзитивности экспертных суждений.

Попарные сравнения позволяют повысить точность оценки, однако недостаток метода заключается в том, что матрица может оказаться несогласованной. В этом случае может потребоваться несколько итераций, что делает процедуру достаточно трудоемкой. В то же время уровень согласованности матрицы позволяет критически оценить качество работы экспертов.

Модифицированный метод анализа иерархий по сравнению с методом Саати позволяет значительно упростить процедуру оценки и уменьшить объем работ при обработке опросных листов. Однако изначально согласованная матрица, не требующая применения итеративной процедуры, лишает руководителя возможности выявить ошибки в работе экспертов. Следовательно, применение ММАИ требует априори предъявлять повышенные требования к опыту и квалификации экспертов.

Суть метода ММАИ заключается в том, что эксперты выносят суждения только для критических ячеек, а не для всех ячеек матрицы. Критическими являются ячейки, расположенные следом за ячейками, находящимися на диагонали матрицы. В табл. 1 выделенные ячейки являются критическими.

Значения для прочих (некритических) ячеек определяются расчетным путем на основе значений критических ячеек. Порядок определения значений некритических ячеек выше диагонали выглядит следующим образом:

а 24 = а 23 × а 34

а 13 = а 12 × а 23

а 14 = а 12 × а 23 × а 34

Таблица 1

Критические ячейки матрицы

Критерий	A	B	C	D
A	1	a 12
B		1	a 23
C			1	a 34
D				1

В ячейки, расположенные ниже диагонали, заносятся обратные значения оценок, таким образом, что a j _i = 1/a_i j .

Применение ММАИ обеспечивает гарантированную согласованность матрицы, поскольку для любой ячейки a ik = a ij × a jk . Кроме того, каждому эксперту в данном случае требуется заполнить лишь (n–1) ячеек вместо n(n–1)/2 ячеек при использовании метода Саати.

Для распределения инвестиций между региональными инвестиционными проектами в данной работе предлагается использовать адаптированный вариант задачи линейного программирования Монжа-Канторовича.

Классическая транспортная задача заключается в нахождении оптимального плана перевозок грузов от поставщиков к потребителям при минимизации транспортных затрат.

Для целей распределения инвестиций адаптированный подход предполагает, что имеется m инвесторов и n инвестиционных проектов. Необходимо распределить имеющиеся средства инвесторов между инвестиционными проектами таким образом, чтобы уровень дисбаланса интересов инвестора и региона-реципиента инвестиций оказался минимальным. При этом уровень дисбаланса определяется как разность между интегральными показателями привлекательности проекта для инвестора и для реципиента.

Результаты

Процедуру распределения инвестиций можно разбить на два этапа, каждый из которых предполагает последовательную реализацию ряда шагов. Схематично методический подход к распределению инвестиций в региональные инвестиционные проекты приведен на рис. 1.

На первом этапе производится оценка региональных инвестиционных проектов. Традиционно для оценки проектов используют набор стандартных показателей (NPV, PI, IRR, PP, DPP и т. д.), которые дают возможность проанализировать генерируемые проектом дисконтированные потоки денежных средств. Такой подход позволяет оценить экономическую привлекательность инвестиционного проекта для инвестора, но при этом не

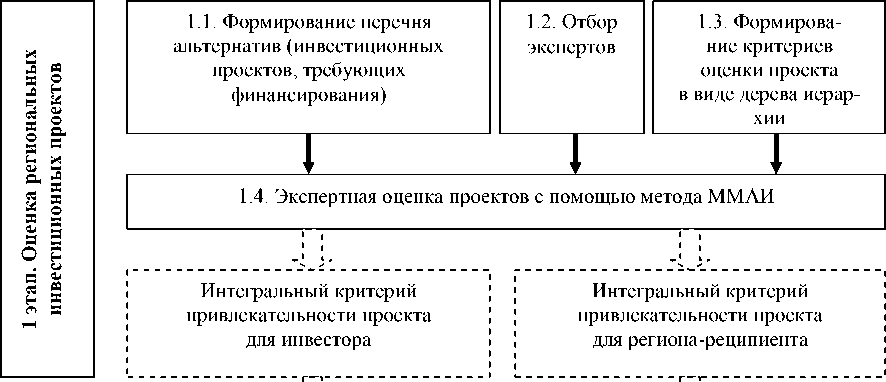
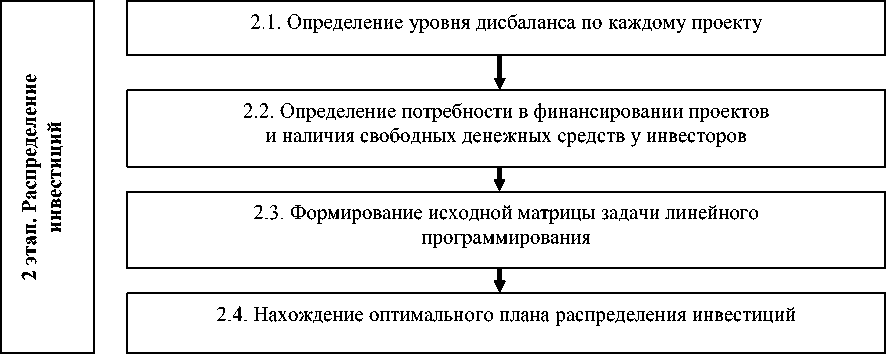
Рис. 1. Схема методики распределения инвестиций в региональные инвестиционные проекты

дает информации о социальных и экологических последствиях реализации проекта. Кроме того, помимо прямой экономической выгоды, проект может приносить инвестору дополнительные преимущества, возникающие как побочный результат реализации проекта.

В силу высокой специфичности крупных проектов возникает проблема с выбором показателей для их критериального оценивания и ранжирования. Особенно актуальной данная проблема становится для проектов с высокой долей инновационной составляющей [16].

Для комплексной оценки проекта предлагается разработать систему критериев, позволяющих наиболее полно оценить последствия инвестиционного проекта как для инвестора, так и для региона-реципиента.

Предлагаемая система оценки включает две группы критериев, первая из которых позволяет оценить последствия реализации проекта для инвестора, а вторая - последствия для региона-реципиента инвестиций. Последствия для инвестора имеют в основном экономический характер, для региона результат будет выражен в большей степени в виде влияния проекта на социальные характеристики региона и экологию.

Система критериев в виде дерева иерархии приведена на рис. 2.

Оценка экономического результата для инвестора осуществляется с точки зрения двух групп критериев: группы, отражающей прямой экономический результат и группы, характеризующей косвенный результат реализации проекта.

Прямой экономический результат оценивается через стандартные интегральные показатели эффективности инвестиционного проекта. Косвенный результат выражается в получении дополнительных нематериальных выгод, которые в даль-

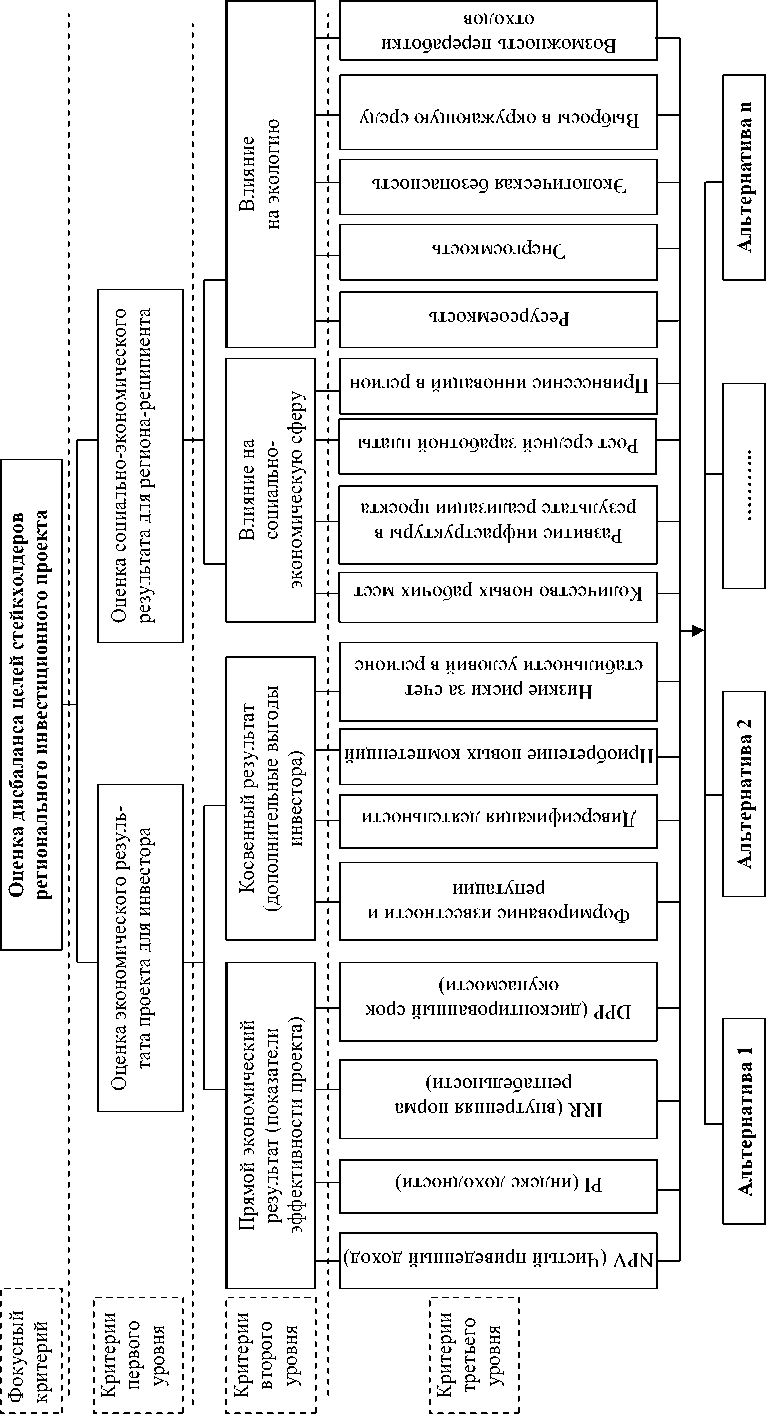
нейшем могут увеличить финансовый результат инвестора. В частности, участие в реализации масштабных, значимых для экономики проектов положительным образом сказывается на формировании репутации. Другими преимуществами для инвестора могут являться снижение рисков за счет отраслевой диверсификации деятельности либо за счет территориального фактора при благоприятных инвестиционных условиях в конкретном регионе, а также приобретение новых компетенций, что позволяет совершенствовать свою деятельность и дает новые возможности роста.

Оценка социально-экономического результата для региона-реципиента также включает две группы критериев: влияние проекта на социальную сферу и влияние на экологическую ситуацию в регионе. Первая группа предполагает оценку прироста рабочих мест и уровня заработной платы, а также влияние проекта на инфраструктуру региона и инновационное развитие. Улучшение данных характеристик в свою очередь стимулирует экономическое развитие региона и обеспечивает благоприятный социальный климат.

Вторая группа критериев включает оценку экологических последствий с точки зрения ресур-соемкости, энергоемкости, экологической безопасности, выбросов в окружающую среду и возможности переработки отходов.

По результатам реализации первого этапа методики каждый из альтернативных вариантов проектов характеризуется двумя индексами: индексом привлекательности проекта для инвестора ( E ) и индексом привлекательности проекта для региона-реципиента инвестиций ( E ).

Второй этап методики предполагает распределение инвестиций в региональные инвестиционные проекты с использованием модели линейного программирования. При определении параметров модели используются относительные показатели, выраженные количественными значениями, полученными путем парных сравнений. Таким образом, данная модель позволяет выполнить оптимизацию распределения инвестиций по качественным критериям.

Распределительная задача линейного программирования для нахождения оптимального плана инвестиций может быть сформулирована следующим образом: пусть имеется m инвесторов (А 1 , А 2 , …, А m ), имеющих в своем распоряжении ресурсы в виде денежных средств, предназначенные для вложения в региональные инвестиционные проекты, в объеме а₁, а₂, …, а_m.

Данные инвестиции следует распределить между n инвестиционными проектами (B1, B2, …, Bn), на реализацию каждого из которых требуется b1, b2, …, bn денежных средств. Также определен уровень дисбаланса интересов инвестора и региона-реципиента dij, который объективно существует как результат рассогласования социально направленных целей региона с экономическими целями инвестора. В данном случае уровень дисбаланса участников (dij) определяется как абсолютное значение разности индекса привлекательности для инвестора и для реципиента dij = E - Ej |.

Необходимо составить план распределения инвестиционных ресурсов, в котором все имеющиеся проекты будут профинансированы за счет всех ресурсов, находящихся в распоряжении инвесторов при минимуме суммарного уровня дисбаланса (предполагается, что в распределении участвуют проекты, предварительно отобранные согласно уровню их эффективности).

Допущением при постановке задачи является условие равенства инвестиционных ресурсов суммарной потребности в денежных средствах для всех имеющихся проектов:

mn

Z ^ai = Z b j . i = i        j = i

Целесообразно представить условие задачи в виде распределительной таблицы (табл. 2), где ресурсы, инвестируемые i-м инвестором в j-й региональный проект являются положительной величиной (x ij >  0), сумма, находящаяся в распоряжении инвестора, и потребность каждого проекта в инвестициях также характеризуются положительными значениями (а_i >  0; b j >  0).

Суммарный уровень дисбаланса можно определить как сумму произведений удельного уровня дисбаланса dij на долю ресурсов в общей сумме х11, направляемых i-м инвестором в j-й инвестиционный проект, что можно выразить в виде следующей целевой функции:

f = d11х11 + d12x12+ d13х13+…+ d1nх1n+…+ mn dm1хm1+ dm2хm2+…+ dmnхmn = Z Zdijaij.

i = i j = i

Нахождение плана распределения ресурсов, при котором целевая функция достигает минимума при заданных ограничениях, будет являться решением задачи. Для решения задачи распределения инвестиционных ресурсов между региональными инвестиционными проектами применяются стандартные методы решения транспортной задачи линейного программирования. В частности, для составления опорного плана может использоваться метод северо-западного угла, метод минимального элемента и т. д. Для проверки плана на оптимальность, как правило, используются метод потенциалов, метод оценки свободных клеток и др.

В данном примере рассмотрен сбалансированный тип распределительной задачи линейного программирования, при котором потребность в инвестициях равна величине ресурсов, находящихся в распоряжении инвесторов. Аналогично можно рассмотреть случай несбалансированной

Распределительная таблица задачи линейного программирования

Таблица 2

Реги ональные инвестиционные проекты Объем имеющихся инвестиций B1 B2 … Bn CL © H CL © я S А1 d11 d12 … d1n a1 x11 x12 … x1n А2 d21 d22 … d1n a2 x21 x22 … x2n … … … … … … … … … … Аm dm1 dm2 … dmn am xm1 xm2 xmn Потребность в инвестициях b1 b1 … bn mn 2 ai = 2 bj i=1         i=1 задачи распределения инвестиций, при которой потребность в инвестициях превышает средства, находящиеся в распоряжении инвесторов либо, наоборот, денежные средства инвесторов превышают необходимые инвестиции.

Обсуждение

В статье рассмотрен двухступенчатый механизм распределения инвестиций в региональные инвестиционные проекты, в основе которого лежат модифицированный метод анализа иерархий и задача линейного программирования распределительного типа. Значительное внимание при этом уделяется возможности учета качественных критериев, что дает возможность дать более полную и объективную оценку последствиям реализации регионального инвестиционного проекта как с точки зрения инвестора, так и с точки зрения самого региона, в котором планируется локализовать данный проект. С целью снижения экспертного субъективизма при оценке количественных и качественных критериев предложено использование метода анализа иерархий, который позволяет разделить процесс принятия решений на более мелкие и интуитивно понятные шаги. Модифицированный вариант метода Саати (предложенный Т. Кимом) кроме того позволяет снизить трудоемкость процедуры и упростить процесс обработки экспертной информации. Применение задачи линейного программирования распределительного типа на втором этапе методики позволяет учесть дисбаланс целей стейкхолдеров при распределении инвестиций.

Предложенный теоретический подход дает представление об особенностях реализации регионального инвестиционного процесса на этапе отбора проектов, а также принимает во внимание различие в восприятии проекта сторонами-участниками, что оказывает влияние на их стимулы в процессе взаимодействия.