К вопросу о технической эффективности инвестиционных проектов

На микроуровне альтернатива M4 (мост + дорога, 4 года) и организационный механизм ее реализации ОЭМ ГП (предполагающий государственно-частное партнерство на всех этапах проекта), выбранные (как наиболее предпочтительные) на предшествующих этапах, подвергаются дальнейшей детализации [1].

Предположим, что Инвестор , получив от проектировщиков технорабочий проект, провел среди строительных организаций транспортного профиля тендер на строительство железной дороги и мостового перехода через пролив Невельского, и по итогам тендера генеральным подрядчиком стала корпорация «Трансстрой» (далее – Генподрядчик ). Допустим также, что эта корпорация из входящих в нее разнопрофильных организаций сформировала единую строительную структуру (назовем ее Подрядчик ), которая должна к заданному сроку построить и сдать в эксплуатацию железнодорожную линию «материк – о. Сахалин» [1].

Постановка задачи оценки КИП «материк – о. Сахалин» на микроуровне в решающей степени определяется тем, что этот проект уникален не только по сложности, но и по объемному цензу (сметной стоимости годового объема строительных работ) Подрядчика. Для исполнения проекта за 4 года строители должны «осваивать» в среднем не менее 135 млрд руб. (в ценах 2018 г.) за год. Примерно столько (28,75 млрд руб. в ценах 2018 г.) ежегодно осваивал Главбамстрой при строительстве БАМ в 1974–1989 гг. [2]. При этом финансирование строительства БАМ шло через МПС, т. е. деньги были государственные, и оплата производилась не за БАМ в целом после при- емки его в эксплуатацию по пусковому комплексу в 1989 году, а по фактически выполненным работам ежеквартально [3]. Это означает, что, во-первых, происходило беспроцентное кредитование подрядчика (Главбамстроя), и во-вторых, у Главбамстроя не было жесткого финансового ограничения по уровню собственных оборотных средств, связываемых в незавершенном строительстве, хотя такое ограничение было у государственного бюджета, который через МПС финансировал строительство БАМ. А поскольку в бюджете страны в последние годы существования СССР денег систематически не хватало, это ограничение срабатывало и БАМ регулярно «недофинансировался» [4]. В результате стройка останавливалась, бригады строителей, машины и механизмы простаивали, технология работ нарушалась. Затем, когда деньги появлялись, следовала «штурмовщина» с неустранимыми при всяком штурме потерями в качестве [5], переплатами за сверхурочные работы, неэффективным использованием техники и прочими непроизводительными издержками [1].

В рыночной экономике роль государства существенно изменилась, отражением этого факта является выбор ОЭМ ГП при оценке проекта на мезоуровне. Для более детального описания ОЭМ ГП на микроуровне мы предполагаем, что [1]:

• •    корпорация «Трансстрой» [6] является генподрядчиком не только по рассматриваемому проекту, но и по другим одновременно выполняемым стройкам с общим годовым объемом работ, в 5 раз превышающим годовой объем по проекту «материк – о. Сахалин»¹;

• •    расчетный счет корпорации регулярно пополняется при оплате работ, выполненных на других объектах; кроме того, корпорация имеет возможность привлекать кредиты, в том числе – иностранные;

• •    ориентируясь на собственные возможности, Генподрядчик определяет для Подрядчика лимит среднегодового (за период строительства) уровня оборотных средств, связываемых в незавершенном строительстве;

• •    в случае недоиспользования указанного лимита Генподрядчик размещает свободные средства на рынке капиталов и убытков не несет;

• •    в случае превышения лимита оборотных средств Подрядчик покрывает строительные затраты за счет кредита по рыночной ставке, превышающей номинальную дисконтную ставку, что увеличивает издержки Подрядчика.

Перед Подрядчиком возникает проблема: разработать такой проект организации работ и координирования деятельности специализированных подразделений, чтобы не превысить лимит сметной стоимости и срок завершения строительства, оговоренные в договоре Генподрядчика (от лица которого действует Подрядчик ) с Инвестором , минимизировать строительные расходы. Это означает максимизацию прибыли Подрядчика от участия в проекте, поскольку его доход зафиксирован договором [1, 7].

Модель денежного потока в форме простейшей сети-цепочки, примененная на мезоуровне для оценки альтернатив Инвестором , недостаточно информативна для микроуровня; Подрядчика не интересуют доходы, которые получит Инвестор в процессе эксплуатации объекта, его проблема заключается в минимизации строительных затрат. Поэтому модель мезоуровня должна быть трансформирована в сетевую модель комплекса строительных работ (операций), в которой денежный поток (затрат) генерируется календарным планом строительства [8]. Понятно, что сетевая модель на этом этапе должна быть укрупненной, поскольку она предназначается не для оперативного управления ходом строительства, а для прогнозирования развития строительного процесса во времени с учетом влияния основных технологических ограничений на параметры денежного потока [1].

Постановка задачи Подрядчика . Предположим, что в рамках заключенного Подрядчиком с Генподрядчиком договора фиксированы [1]:

• •    срок окончания строительства железной дороги в целом Т _д ;

• •    конструктивные решения по объектам строительства;

• •    режим оплаты генеральным подрядчиком сметной стоимости работ в период строительства;

• •    сметная стоимость объекта в целом как фиксированная сумма сметных стоимостей работ.

Кроме того, с Генподрядчиком согласован сетевой график строительства дороги и моста. Это означает, что, рассмотрев сетевой график [9], разработанный Подрядчиком , Генподрядчик , во-первых, согласился с допустимостью отраженных в нем организационно-технологических решений, и во-вторых, выразил готовность оплатить затраты подрядчика после приемки готовых объектов в оговоренных контрактом объемах и сроках. Отсюда следует, что Инвестор оплачивает подготовленную к эксплуатации дорогу без промежуточных платежей, а Подрядчик ведет строительство за счет лимита оборотных средств, выделенных Генподрядчиком , прибегая при необходимости к банковским кредитам² [1].

При указанных условиях перед Подрядчиком возникает проблема выбора рационального календарного плана производства работ на объектах строительства. Будем в дальнейшем полагать, что критерием рациональности допустимых календарных планов [10] является минимум издержек Подрядчика на строительство объектов, входящих в состав только проекта «материк – о. Сахалин». Другими словами, мы предполагаем, что Подрядчик не строит никакие объекты вне рассматриваемого проекта. Допустим также, что Подрядчик ведет все работы только собственными силами. Тогда он должен из ограниченных собственных финансовых ресурсов покрывать затраты на незаконченное строительство так, чтобы, не нарушая технологические ограничения, гарантировать завершение строительства объекта в договорный срок. Предполагается, что договорные санкции за нарушение Подрядчиком срока завершения строительства запретительно высоки [1].

Формализуем проблему³. Предположим, что известна укрупненная сетевая модель строительного проекта, то есть ориентированный граф без контуров (сеть) G = ( X , Ω), где X – множество вершин (событий), Ω – множество дуг (работ) сети G . Заданы ранняя возможная дата начала строительства объекта Т ₀ и срок завершения строительства объекта Т _д . Для каждой работы ( i , j ) ∈ Ω определены сметная себестоимость c ij (сметная стоимость за вычетом нормативной прибыли) и продолжительность t ij (в принятых единицах времени), целое число [1].

Нужно найти календарный план строительства объекта: x = ( T ij | ( i , j ) ∈ Ω), где T ij – срок начала работы ( i , j ) [1].

Искомый календарный план должен удовлетворять следующим условиям:

Т0 ≤ Tij ≤ Тд, (i, j) ∈ Ω;(1)

Tij + tij ≤ Tjk , (i, j) ∈ Ω, ( j, k) ∈ Ω;(2)

Tij целые, (i, j) ∈ Ω.(3)

Пусть t ∈ { Т 0 + 1, … , Т д } и x = ( T ij | ( i , j ) ∈ Ω) – произвольный календарный план, удовлетворяющий условиям (1)–(3). Опишем множество работ, происходящих в единичный период [ t – 1; t ] при плане x [1]:

Ωt (x) = {(i, j) ∈ Ω | t ≤ Tij + tij, Tij < t} = {(i, j) ∈ Ω | t – tij ≤ Tij ≤ t – 1}.(4)

Предположим, что финансовые ресурсы Подрядчика на каждой работе ( i , j ) ∈ Ω расходуются равномерно в течение ее выполнения. Тогда интенсивность использования средств на работе ( i , j ) не зависит от календарного плана и равна c ij / t ij . Потребность в оборотных средствах на строительство рассматриваемого объекта в промежутке [ t – 1; t ] при календарном плане x описывается следующим образом [1]:

F t ( x ) = ∑ ^cij .                                                                             (5)

( i , j ) ∈ Ω _t ( x ) t ij

Пусть A ( t ) – величина оборотных средств, предназначенных Подрядчиком для покрытия осуществляемых в промежутке [ t – 1; t ] затрат на строительство объекта. Введем обозначения для моментов начала и конца строительства при плане x [1]:

T 0 ( x ) = min{ T ij | ( i , j ) ∈ Ω}, T 1 ( x ) = max{ T ij + t ij | ( i , j ) ∈ Ω}.                                         (6)

T 1 ( x )

Величина p ( x ) = Е F t ( x ) - A (^х)| характеризует «финансовую неравномерность» (далее t = T 0 ( x ) + 1

аритмия ) процесса строительства при плане x , возникающую из-за несовпадения потребности в оборотных средствах в периоде [ t – 1; t ] и их наличия у Подрядчика ; аритмию ρ( x ) желательно минимизировать [1].

Величину связывания оборотных средств Подрядчика (далее – связывание) при плане x хат д рактеризует величина c(x) = Е (Тд -t)Ft(x), которую тоже хотелось бы уменьшить4 [1].

t = T )( x ) + 1

Можно выбрать критерий оптимальности следующим образом [1]:

р ( x ) ^ min, ст ( x ) ^ min.

Имеем векторный критерий оптимальности (p( x ), ^ ( x )), компоненты которого, вообще говоря, несогласованны: календарные планы, оптимальные по одному из указанных критериев, в общем случае не оптимальны по другому критерию. Укажем два подхода к нахождению предпочтительного (компромиссного) плана [1].

Первый подход . Критерии p( x ) и o ( x ) имеют одинаковую размерность (руб.хгод) и по сути являются ресурсно-технологическими. В пространстве этих критериев существует область, образованная календарными планами, допустимыми по условиям (1)–(3). «Юго-западную» границу этой области образуют точки, соответствующие планам, оптимальным по Парето [13]. Компромиссный план находится посредством скаляризации критерия (7) через введение дополнительной (внемодельной) экономической информации в виде взвешивающих коэффициентов при слагаемых, входящих в функции p( x ) и o ( x ) [1].

А именно, ρ( x ) заменим на

T 1 ( x )

R(x) =   Е If(x) - A(t)l -vt(x), t=To( x)+1

где ψ _t ( x ) – «цена несовпадения» потребности в финансовых ресурсах и их наличия у Подрядчика в периоде t при плане x [1]:

V t ( x ) =

_ Vt, .V 2,

если если

F t ( x ) ^ A ( t ), F t ( x ) <  A ( t ).

Компоненту a ( x ) заменим на

т

д

S(x) = Е (1 + r)-F (x), t=To+1

где r – ставка приведения разновременных затрат к моменту начала строительства.

Будем считать предпочтительным тот допустимый календарный план x , который минимизирует скалярный критерий

[ R ( x ) + S ( x )],                                                                                         (11)

понятно, что этот календарный план лежит на кривой Парето [1].

* * *

Построим укрупненную сетевую модель процесса строительства железной дороги и моста за 4 года в соответствии с альтернативой M4 . Предварительно оговорим организационноэкономические предпосылки, которые определят структуру модели и значения ее параметров. Перейдем от календаря в годах, использованного на мезоуровне, к календарю в кварталах; период строительства равен 16 кварталам. Капитальные затраты будем измерять не в миллиардах, как на макроуровне, а в миллионах долларов [1].

Подрядчик планирует осуществлять строительство в четыре потока (луча).

Первый поток : строительство железной дороги от ст. Селихин до середины участка Сели-хин – Черный мыс, сметная стоимость 102 млрд руб. в ценах 2018 г.

Второй поток : строительство железной дороги от моста до середины участка Селихин – мыс Лазерва, сметная стоимость 102 млрд руб. в ценах 2018 г.

Третий поток : возведение моста через пролив Невельского, сметная стоимость 253 млрд руб. в ценах 2018 г.

Четвертый поток : строительство железной дороги от моста до станции Ныш на Сахалине, сметная стоимость 83 млрд руб. в ценах 2018 г.

Допустим, что за каждым потоком закреплены мощности подразделений Подрядчика , величина которых определяет общую длительность выполнения соответствующих работ. Предположим, что интенсивность освоения сметных средств на каждом потоке постоянна. Тогда, разделив сметную стоимость потока на его длительность, найдем интенсивность потока – сметную стоимость работ, выполняемых в каждом квартале. Информация о строительных потоках сведена в табл. 1 [1].

Таблица 1

Характеристики строительных потоков

Номер потока	Сметная стоимость (млн долл.) [14]	Длительность (квартал)	Резерв времени (квартал)	Интенсивность (млн долл./квартал)
1	102	7	9	15
2	102	7	9	15
3	253	16	0	16
4	83	2	14	42

На рис. 1 приведена сетевая модель проекта, в которой потокам 1, 2, 3, 4 сопоставлены дуги-работы (1, 2), (1, 3), (1, 5), (1, 4) соответственно; работа ( i , j ) имеет длительность t ij и сметную стоимость c ij . Ясно, что технологически строительные работы по всем 4 лучам могут быть начаты одновременно и производиться с заданной интенсивностью. Критический путь (1, 5) наибольшей длины определяет срок завершения всего строительства. Некритические работы, входящие в остальные три луча, имеют резервы времени. В границах этих резервов некритические работы (целиком, без разрывов) могут сдвигаться вправо по календарной шкале до тех пор, пока резервы времени не будут использованы полностью. Таковы степени свободы, в рамках которых работы могут независимо перемещаться, образуя совместно с критическим путем различные технологически допустимые календарные планы. На рис. 1 изображен «левый» календарный план строительства x ⁰, при котором все работы начинаются как можно раньше [1].

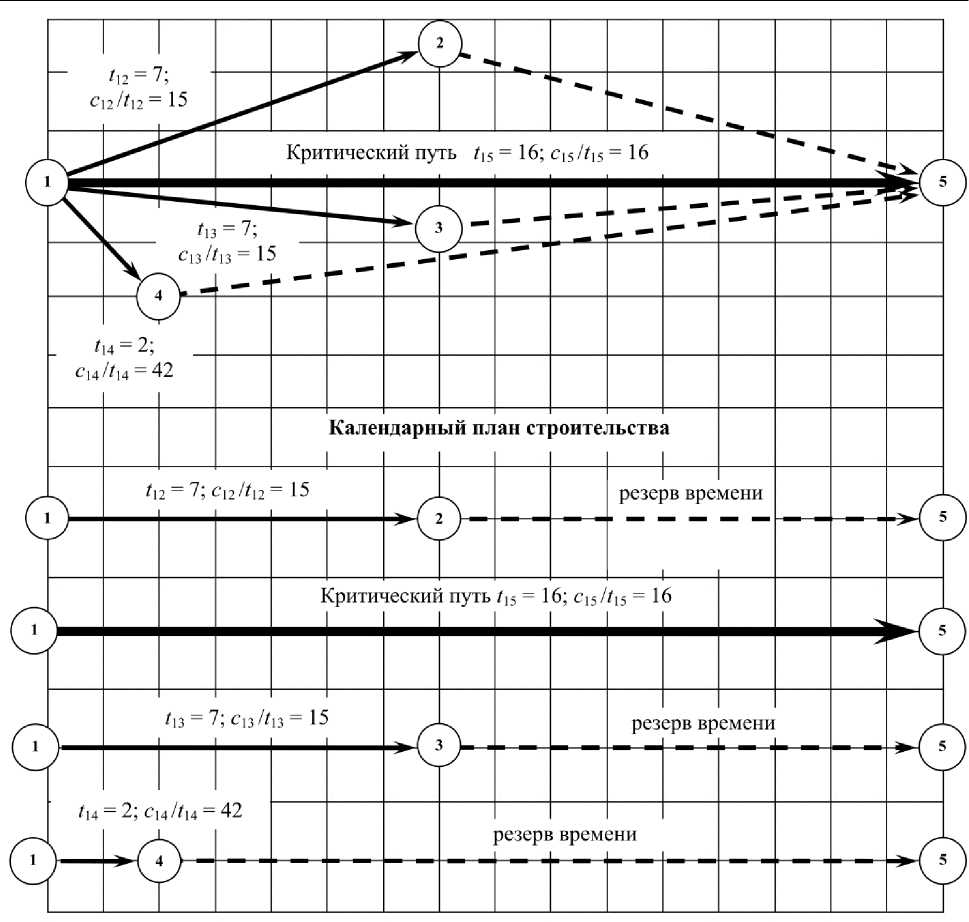
Кварталы расчетного периода на этапе строительства

Рис. 1. Сетевая модель и «левый» календарный план строительства

Задача состоит в том, чтобы из числа допустимых выбрать наиболее предпочтительный календарный план. Для выбора такого плана в рамках принятой выше постановки мы используем критерии R ( x ) и S ( x ). Чтобы минимизировать связывание средств S ( x ) с учетом фактора времени, все работы, имеющие резервы, должны начинаться как можно позже, что соответствует «правому» [15] плану x ¹, оптимальному по критерию S ( х ). Однако этот план порождает неравномерную (по интервалам расчетного периода) потребность в финансовых средствах, необходимых для обеспечения бесперебойного хода строительных работ. В результате возникает ущерб от аритмии R ( x ¹), связанный как с недостатком финансовых ресурсов в некоторых кварталах (когда Подрядчик прибегает к внешнему кредитованию), так и с излишком оборотных средств (когда происходят потери упущенной выгоды). Необходимо сформировать план, минимизирующий сумму указанных выше потерь. Решение проблемы проиллюстрируем с помощью рис. 2–4. На этих рисунках над дугами-работами указаны поквартальные сметные затраты [1].

На рис. 2 изображен безрезервный «правый» план x ¹. Время на микроуровне измеряется в кварталах, следовательно, при сроке строительства 4 года t ∈ {1, …, 16}. Пусть годовая ставка дисконта равна 10 %. Соответствующая квартальная ставка r вычисляется следующим образом: r = ⁴ 1,1 – 1 ≈ 0,024. Поквартальный график потребности в оборотных средствах при плане x ¹ построен в нижней части рис. 2. По формуле (10) при T 0 ( x ¹) = 0 и T д = 16 найдем приведенные затраты Подрядчика при плане x ¹: S ( x ¹) ≈ 418,70 млрд руб. в ценах 2018 г. [1].

Рис. 2. «Правый» календарный план строительства

									15	15	15	15	15	15	15
16	16	16	16	16	16	16	16	16	16	16	16	16	16	16	16
									15	15	15	15	15	15	15
														42	42
														88	88
									46	46	46	46	46
				Уровень оборотных средств Подрядчика A(t) = 31
16	16	16	16 Ква	16 рталь	16 расч	16 пнок	16 । пери	16 ада Hi	этап*	1 CTpOl	ггелы	:тва

Допустим, что при избытке собственных оборотных средств Подрядчик не несет издержек упущенной выгоды, так как размещает свободные средства на рынке по квартальной ставке не ниже 2,5 %, а при недостатке средств вынужден их заимствовать по спекулятивной квартальной ставке 9 %.

Положим, ψ ¹ _t = 0 для всех t и ψ _t ² = 1,09^{– t} в (9). Это значит, что при оценке ущерба от аритмии мы не учитываем избыток оборотных средств, а недостаток оборотных средств дисконтируем к началу расчетного периода с нормой приведения 9 %. Применив формулу (8) при T 0 ( x ¹) = 0 и T ₁ ( x ¹) = 16, найдем издержки ликвидации аритмии при «правом» плане: R ( x ¹) ≈ 56,87 млрд руб. в ценах 2018 г. [1].

		5	15	15	15	15	15	15
	1	6	16	16	16	16	16	16	16	16	16	16	16	16	16	16	1	6 5
									15	15	15	15	15	15	15
																42	4	2
						Уров	ень об	0РОТНЕ	.ix cpej	зств п	одряд	чика Л	(0 = 3	1		58	58

1     2    3    4    5    6    7    8    9   10 11    12 13   14   15 16

Рис. 3. «Равномерный» календарный план строительства

Подставим в (11) значения S ( x ¹) и R ( x ¹): R ( x ¹) + S ( x ¹) ≈ 475,56 млрд руб. в ценах 2018 г. [1].

План x ² лучше плана x ¹ по критерию (11), однако на рис. 4 указан еще лучший план.

15	15	15	15	15	15	15
	16	16	16	16	16	16	16	16	16	16	16	16	16	16	16
									15	15	15	15	15	15	15
														42	42
														73	73
				Урове	;нь обе	эротнь	IX сре;	1ств П	одряд	чика /,	(0=з	1

1     2    3    4    5     6     7    8     9    10 11   12   13   14   15 16

Рис. 4. «Компромиссный» календарный план строительства

Подставляя значения, полученные при «компромиссном» плане x ³, в формулу (10) при T 0 ( x ³) = 0, T д = 16 и r = 0,024, найдем R ( x ³) ≈ 437,08 млрд руб. в ценах 2018 г. При ψ ¹ _t = 0 для всех t , ψ _t ² = 1,09^{– t} , T 0 ( x ³) = 0 и T 1 ( x ³) = 16 дает S ( x ³) ≈ 22,11 млрд руб. в ценах 2018 г. Следовательно, R ( x ³) + S ( x ³) ≈ 459,19 млрд руб. в ценах 2018 г.

Ниже мы прокомментируем полученный результат.

* * *

Выше, сравнивая календарные планы, мы применяли критерий (7), используя, в соответствии с формулами (9) и (10), взвешивающие коэффициенты ψ ¹ _t , ψ _t ² и (1 + r )^{– t} [1].

Каждому календарному плану x можно сопоставить точку ( ρ ( x ), σ ( x )) в координатах ( ρ , σ ) (рис. 5). Календарному плану, полученному с помощью имитации и наиболее предпочтительному по критерию (7), соответствует одна из эффективных (Парето-оптимальных) точек на кривой Парето AB [1, 15].

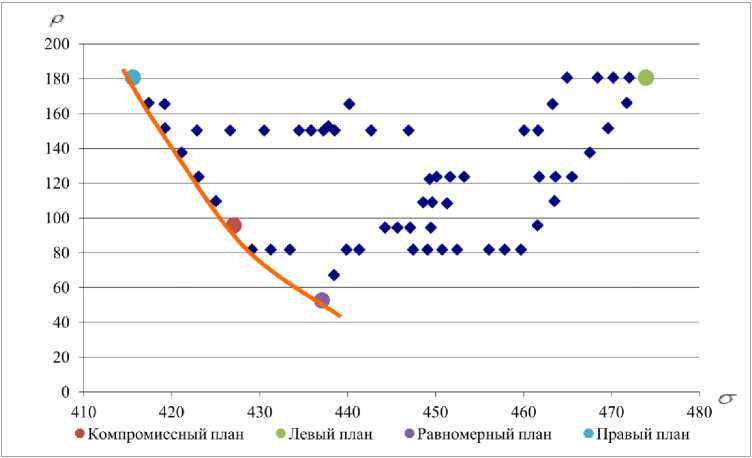
Рис. 5. Эффективные по Парето календарные планы, полученные с помощью имитации

Сведем для удобства все полученные результаты в табл. 2.

Сводная

Таблица 2

№	Календарный план	R ( x ) + S ( x ) млрд руб. в ценах 2018 г.
1	«Левый» x 0	632,17
2	«Правый» x 1	475,56
3	«Равномерный» x 2	459,48
4	«Компромиссный» x 3	459,19

Выражаю благодарность своему научному руководителю Евгению Борисовичу Кибалову за ценные советы при планировании исследования и рекомендации по оформлению статьи.