К вопросу о внедрении автоматизированных способов расчета показателей надежности электрических сетей в практику деятельности сетевых предприятий

Введение. Одной из первоочередных задач сетевых предприятий района электрических сетей (РЭС) является обеспечение надежного электроснабжения потребителей. Анализ исследований ряда авторов [1, 2, 3] показал, что для распределительных электрических сетей агропромышленного комплекса эта задача не решена в полной мере, и проблема повышения эксплуатационной надежности остается актуальной. В научной литературе содержится большое количество предложений технического и организационного характера, направленных на решение частных задач проблемы повышения надежности функционирования электрических сетей [4, 5, 6]. Для практической оценки эффекта от внедрения того или иного мероприятия в каждом конкретном случае необходимо располагать информацией о показателях надежности исследуемой системы. Кроме того, объективная и своевременная информация о показателях надежности электрической сети может быть использована энергоснабжающей организацией для заключения договоров с абонентами на отпуск электроэнергии, может позволить более четко организовать работу подразделений РЭС, рационализировать выполнение эксплуатационных мероприятий, что особенно актуально для АПК.

Традиционно информация об отказах элементов электрических сетей, вызывающих перерыв в электроснабжении потребителей, фиксируется оперативно-диспетчер-ским персоналом в журнале отключений. Среди прочей информации в таких журналах указывается вид отключения и длительность перерывов электроснабжения. В зависимости от вида отключения бывают плановые и неплановые, последние в свою очередь могут быть аварийными и неотложными.

Для проведения исследований в большей степени интерес представляют именно аварийные отключения, поскольку они имеют случайный характер и могут приводить к возникновению серьезного ущерба у сельскохозяйственных потребителей, особенно в зимние периоды. Поскольку количество и продолжительность аварийных отключений является случайной величиной, то для расчета показателей надежности вполне закономерно использовать методы математической статистики и теории вероятностей. Эти методы хорошо известны научной общественности [7, 8, 9, 10] и их эффективность для расчета показателей надежности электрических сетей не вызывает сомнений.

Однако в практике сетевых предприятий, осуществляющих эксплуатацию сельских электрических сетей, расчеты показателей эксплуатационной надежности электросетевого оборудования не получили широкого распространения, что может быть связано с достаточной трудоемкостью этих расчетов и необходимостью специальных знаний математического аппарата. Развитие информационных технологий в настоящее время позволяет значительно упростить решение этой задачи путем внедрения автоматизированных способов обработки статистических данных о показателях надежности электрических сетей в практику деятельности сетевых предприятий.

Материалы и методы исследований. Основными показателями надежности электрических сетей являются показатели, характеризующие свойства безотказности – параметр потока отказов (в нашем случае – потока аварийных отключений) и ремонтопригодности – среднее время восстановления электроснабжения. Располагая информацией о них, можно определить комплексные показатели надежности, такие как коэффициент готовности и коэффициент технического использования, а также вероятность безотказной работы.

Поскольку расчет показателей надежности производится методами математической статистики, то выборочная совокупность данных об аварийных отключениях должна иметь большой объем (желательно более сотни). Анализ журналов отключений показал, что соответствующий объем данных в среднем может быть накоплен за три года.

Параметр потока аварийных отключений для линий электропередач представляет собой среднее количество аварийных отключений линий в год, отнесенное к единице её длины. Соответственно за год для данного района электрических сетей этот показатель может быть рассчитан по формуле

N

E L r = i=1 Li j    N ’ где ri - число отключений i-й линии;

L i - протяженность i - й линии, км;

N – число фидеров.

С учётом периода накопления статистической информации параметр потока аварийных отключений следует определять как

n

£ r j

Р а = i=^

n где n – число лет сбора информации.

Поскольку в настоящее время журналы отключений в РЭС ведутся в электронном виде, то выбрать необходимый объем данных о количестве аварийных отключений по ним не составляет особого труда.

Для автоматизации обработки этих данных может быть использован, например, табличный редактор Excel. Предлагаемая форма таблицы представлена на рисунке 1.

Строки со значениями для r i и L i заполняются вручную, данные в остальных ячейках рассчитываются автоматически, по описанным выше формулам. На рисунке 1 приведены результаты расчета потока аварийных отключений для сетей 10 кВ одного из РЭС Северо-Кавказского региона.

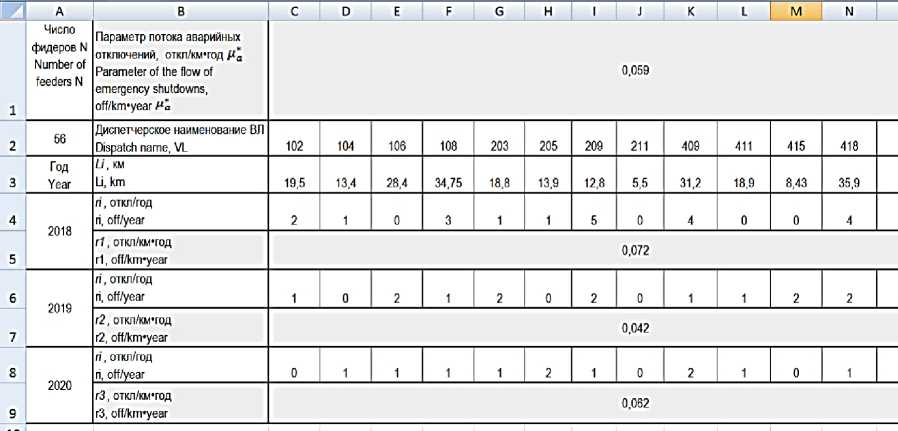
Рисунок 1 – Фрагмент таблицы для определения параметра потока аварийных отключений

Figure 1 – Fragment of the table for determining the parameter of the flow of emergency shutdowns

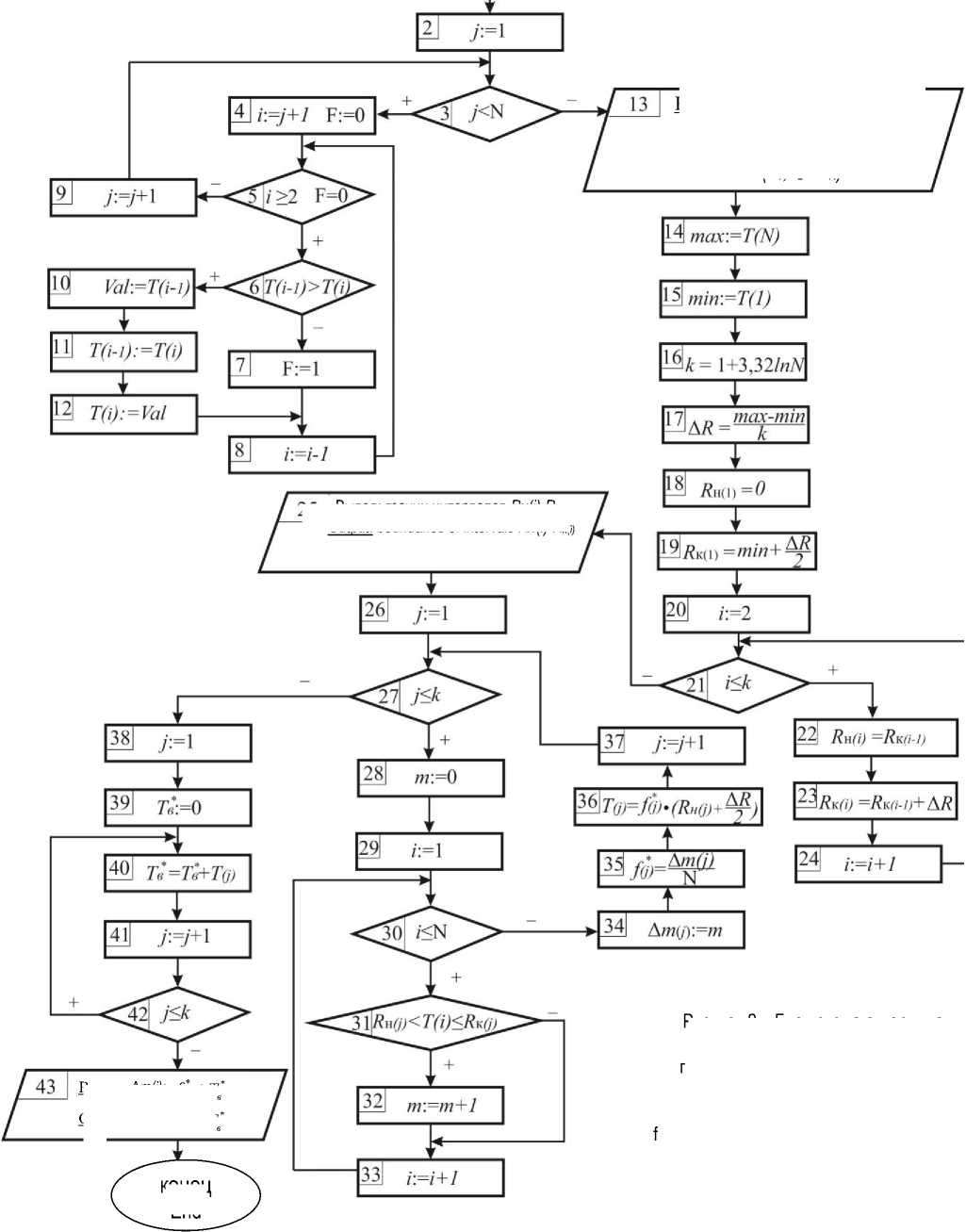
Для определения второго показателя надежности – среднего времени восстановления Т * необходимо найти статистическое распределение выборочной совокупности данных, которое может быть представлено в виде гистограммы частот. Для автоматизации этого процесса предлагается алгоритм, представленный на рисунке 2.

В соответствии с представленным алгоритмом в блок 1 необходимо ввести данные из журнала отключений о длительности перерывов электроснабжения T(n) , вызванных аварийными отключениями.

Блоки со 2 по 13 обеспечивают формирование и вывод вариационного ряда, представляющего собой расположенные в порядке возрастания периоды времени, соответствующие времени восстановления электроснабжения ( T 1 , T 2 , … T N ). Благодаря блокам с 14 по 25 вариационный ряд разбивается на k частных интервалов и происходит определение их границ ( R н(i) – R к(i) ). В частности, в блоке 16 определяется необходимое количество интервалов ( k ), в блоке 17 рассчитывается их ширина ( ΔR ), а в блоках с 18 по 25 определяются их границы ( R н(i) – R к(i) ).

В блоках с 26 по 37 происходит подсчет количества аварийных отключений Am®, продолжительность которых соответствует /-ому интервалу и рассчитывается относительная частота f ∗ появления случайной величины – времени восстановления электроснабжения в данном интервале.

Вывод: вариационного ряда

конец End

Figure 2 – Block diagram of the algorithm for processing statistical data on the duration of outages

j Вывод: границ интервалов RK(i)-R k(i) Output: boundaries of intervals RH(i)-R k(i)

Вывод: Д m(i); f ; T ( j )

Output: Д m(i); f * ; T ( j )        в

Рисунок 2 – Блок-схема алгоритма обработки статистических данных по продолжительности отключений

В блоках с 38 по 42 подсчитывается среднее статистическое значение времени восстановления

k

*=v *,

Tв =∑ fi ⋅ti , i=1

∗ где ti – среднее значение времени для каждого из интервалов, ч.

Результаты исследований и их обсуждение.    В соответствии с предложенным алгоритмом был обработан массив данных по аварийным отключениям за три года для одного из РЭС СевероКавказского региона, в результате получено статистическое распределение, представленное в виде таблицы и гистограммы частот (рисунок 2). Среднее время восстановления составило для рассматриваемого РЭС Тв =1,92ч.

Статистические частоты появления аварийных отключений различной длительности

Statistical frequencies of occurrence of emergency shutdowns of various durations

Rh@ - Rk@ , h.	<1]	(1–2]	(2–3]	(3–4]	(4–5]	(5–6]	(6–7]	(7–8]	>8)
^m( j)	70	45	30	15	7	5	4	3	1
∗ i , r.u.	0,389	0,250	0,167	0,083	0,039	0,028	0,022	0,017	0,006

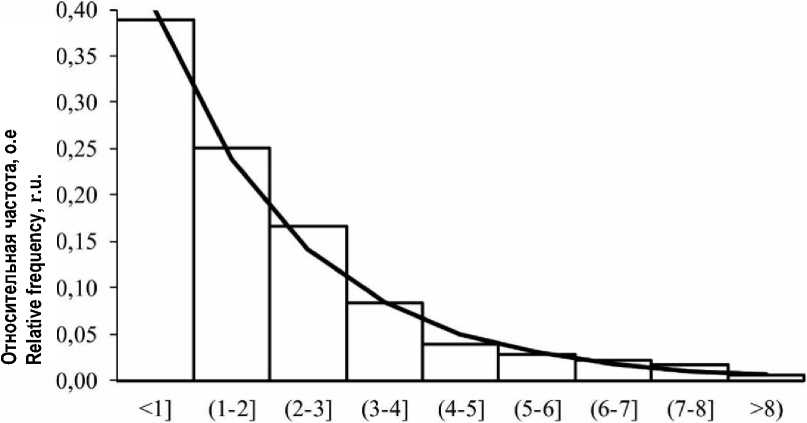
Продолжительность отключения, ч

Shutdown duration, h

Рисунок 3 – Гистограмма продолжительности отключения, совмещенная с теоретической кривой плотности вероятности времени восстановления

Figure 3 – Histogram of the duration of the outage, combined with the theoretical probability density curve of the restoration time

Для проведения аналитических исследований удобно использовать одну из математических моделей теории вероятностей. Анализируя полученное статистическое распределение времени восстановления электроснабжения, можно выдвинуть гипотезу о том, что оно подчинено экспоненциальному закону, для которого плотность вероятности времени между отказами описывается зависимостью:

f (t) = X- e- Xt, где Я - интенсивность отказов, X = -1

T в

.

Интегральная функция распределения для экспоненциального закона имеет следующий вид:

F ( t ) = 1 - e ^{- x t} = 1 - e^T .

Теоретическое значение частот для каждого из интервалов может быть определено как приращение функции F(t) при переходе к следующему интервалу.

На рисунке 3 построена теоретическая кривая плотности вероятности времени восстановления, совмещенная с гистограммой статического распределения.

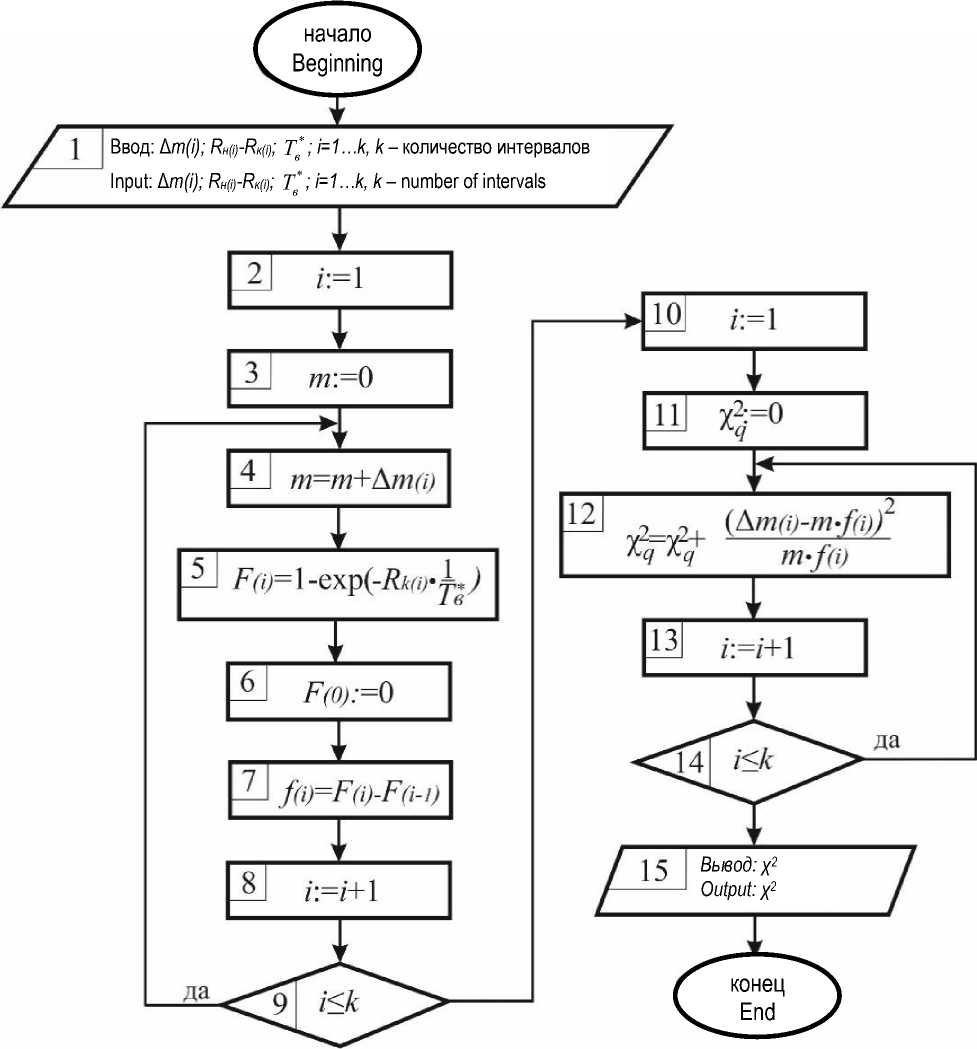
Рисунок 4 - Блок-схема для расчета критерия х 2 Figure 4 - Block diagram for calculating the criterion х 2

Чтобы доказать, что выборочные подчиняющихся экспоненциальной модели данные взяты из совокупности данных, распределения, используем критерий согласия    χ2-Пирсона.     Методология проведения согласования по данному критерию достаточно хорошо описана в учебных изданиях по статистике. Нами предлагается алгоритм, который позволяет автоматизировать этот процесс.

В соответствии с блок-схемой алгоритма, представленного на рисунке 4, может быть произведен расчет критерия x q .

Вероятность того, что случайная величина меры расхождения χ² примет значение не меньше, чем наблюдаемое значение ² :

^x q

P = ^PS ( X ² >  Z q ² ) является функцией x 2 и параметра s , называемого числом степеней свободы.

Число      степеней      свободы определяется по формуле s=k - g-1, где g – число параметров теоретического закона распределения, определяемое на основе статистических данных. Для экспоненциального закона g = 1, тогда s = 7.

Имея значения x2 и s, можно воспользоваться таблицами, приводимыми в литературе по математической статистике, и определить вероятность Рs. При этом, если Рs > 0,1, то гипотеза о том, что статистическое распределение может быть описано аппроксимирующей функцией, принимается. Если же величина Рs окажется меньше 0,1, то гипотезу следует отвергнуть, выбрать другой вид аппроксимирующей функции и вновь проверить эту гипотезу по указанному критерию согласия.

Расчеты, проведенные в соответствии с представленным на рисунке 4 алгоритмом, позволили определить значение x2 = 2,22. Далее была определена вероятность Рs при числе степеней свободы s = 7, которая составила 0,95, что свидетельствует о том, что принятая к рассмотрению гипотеза об экспоненциальном законе распределения времени восстановления электроснабжения при аварийных отключениях может быть принята.

Выводы. Для получения достоверных значений показателей эксплуатационной надежности сельских электрических сетей необходимо производить обработку достаточно большого массива данных. Предлагаемые в статье алгоритмы обработки данных могут значительно упростить данный процесс. Выполненные в соответствии с разработанными алгоритмами расчеты показателей надежности для одного из районов электрических сетей Северо-Кавказского региона позволили, в результате обработки данных о длительности и количестве аварийных отключений за три года, определить значение параметра потока аварийных отключений для сетей 10 кВ, равного 0,059, установить, что продолжительность восстановления электроснабжения при аварийных отключениях подчиняется экспоненциальному закону и среднее время восстановления составляет 1,92 часа.