К вопросу о зональности побега на примере побегов Acer negundo L.
Автор: Антонова Ирина Сергеевна, Барт Виктор Александрович
Журнал: Вестник Тверского государственного университета. Серия: Биология и экология @bio-tversu
Рубрика: Ботаника
Статья в выпуске: 4, 2015 года.
Бесплатный доступ
В течение многих лет на разных видах деревьев отмечалось совпадение верхних частей элементарных побеговых систем при наложении. В работе создан математический аппарат и подготовлен статистический массив данных, позволяющие вскрыть морфологические причины этого явления. Проведено описание междоузлий побегов массива данных, состоящего из 86 двулетних побеговых систем, собранных из трех популяций A. negundo Белгородской и Ленинградской областей. На основе анализа главных компонент ковариационной матрицы установлена система строгих соотношений длин междоузлий как верхнего, так и нижнего концов побега. Выявленные эффекты приводят к большой схожести распределений крайних междоузлий, наблюдаемой у побегов всего массива данных различных лет, а также места происхождения и местоположения самого побега в кроне.
Побег, междоузлие, крона, побеговая система, доверительный эллипсоид рассеяния, корреляционные плеяды, ковариационная матрица, главные компоненты
Короткий адрес: https://sciup.org/146116605
IDR: 146116605 | УДК: 581.441:
Текст научной статьи К вопросу о зональности побега на примере побегов Acer negundo L.
Крона дерева представляет собой систему побегов разной длительности жизни. Растение изменением формы отвечает почти на любое воздействие среды. Тем не менее, крона дерева конкретного вида узнаваема даже в безлистном состоянии, что возможно лишь при условии подчинения развития определенной программе, свойственной виду. При практической работе по выявлению структуры модели кроны большое значение имеет анализ различных свойств побега (Maillette, 1982, 1987; Wilson, 1989; Антонова, Азова, 1991; Антонова, Николаева, 2004; Barthelemy, Caraglio, 2007; Антонова, Фатьянова, 2012).
На фоне применения дифференциальных уравнений для описания процессов развития побегов мало внимания уделяется точному описанию начальных и последних междоузлий. В частности, в моделировании кривой Сакса роста побега формирование последних междоузлий как правило требует формально бесконечного промежутка времени для дорастания, в связи с чем их рост обычно в работах не рассматривается (Сабинин, 1963; Савинов и др., 1976). В современном моделировании развития побега делаются серьезные попытки подключить математический аппарат случайных процессов (Chaubert-Pereira et al., 2010, Prusinkiewicz, Lindenmayer, 2012). В математике случайный процесс может быть охарактеризован как последовательность случайных величин или как набор случайных реализаций во времени (Колмогоров, 1936; Ито, I960). В математических моделях при оценке параметров случайного процесса исследователь, в основном, стремится представить процесс в одном времени. В итоге, целостная картина развития междоузлий на побеге выпадает.
Морфологи растений получают данные о побеге как набор реализаций. В таком представлении Н.П. Кренке (Кренке, 1940, 2015) пришел к осознанию параллельного присутствия двух равноправных масштабов времени развития, причем междоузлия верхнего края побега представляют собой особую в морфологическом и физиологическом смысле зону. Именно в этих междоузлиях у многих акротонно развивающихся деревьев, например, у Acer negundo, располагаются боковые побеги наибольшей длины, несмотря на то, что боковые почки этой зоны не имеют максимальной ёмкости (Фатьянова, Антонова, 2010; Антонова, Гниловская, 2013).
Цель исследования: выявить зональную структуру групп междоузлий побега A. negundo, обусловленные этапами его развития.
Методика. Материалом исследования послужили побеги растений 3-х разных местообитаний. Два из них находятся в заповеднике «Белогорье» (Белгородская обл.): одно на опушке нагорной дубравы, второе - в долине пересыхающего ручья. Третье местообитание располагается на полосе отчуждения заброшенной железной дороги на берегу Финского залива в 2 км от Санкт-Петербурга. Все растения находились в виргинильном и молодом генеративных состояниях и произрастали при отсутствии затенения. Материал в количестве 38 особей был собран в вегетационные сезоны 2013-2015 гг.
В ходе исследования были подробно описаны все 4 порядка ветвления особей. Определён год появления каждого побега, его длина, количество листьев, размеры междоузлий, характер развития почек и углы ответвления боковых побегов от материнского. Составлены подробные схемы расположения побегов. Всего было исследовано 1329 побегов, в том числе 86 двулетних побеговых систем. Рассмотрены побеги осей первого порядка (стволов) и наиболее мощные кронообразующие оси второго порядка.
Обработка данных проводилась с помощью пакета программ STATISTICA 6.0 (StatSoft, Inc.) в блоках корреляционного, дисперсионного (ANOVA), многомерного дисперсионного и факторного анализов. Применен метод корреляционных плеяд
В.П. Терентьева, для которого была написана компьютерная программа на языке STATISTICA Visual Basic. Предложен метод описания свойств концевых междоузлий для больших массивов побегов, основанный на факторном анализе как корреляционной, так и ковариационной матриц.
Обозначение междоузлий побегов проведено двумя разными способами. В первом случае - арабскими цифрами, междоузлия пронумерованы от первого к последнему согласно их расположению на побеге в ходе образования и развития: 1 - первое междоузлие, подлежащее первой паре почечных чешуй, 2 - второе междоузлие, подлежащее второй паре почечных и т.д. Во втором случае междоузлия пронумерованы от верхнего конца побега и обозначены прописными буквами русского алфавита: «а» - верхнее короткое междоузлие под верхушечной почкой, последнее в ходе развития данного побега, «б» -нижележащее, ближайшее к верхнему междоузлию, «в» - следующее от конца побега и т.д. Такая система обозначений позволяет сразу выделять концевые междоузлия, различать и сравнивать верхний и нижний концы побега вне зависимости от количества листьев на нем. В силу акротонного развития боковые побеги наибольшей величины развиваются у Л. negundo в верхних междоузлиях материнского побега, что было описано ранее (Антонова, Гниловская, 2013). В данной работе также уделяется внимание признакам «длины боковых побегов». Они обозначены заглавными буквами, соответствующими подлежащему ему междоузлию, т.е. на междоузлии «а» материнского побега развивается боковой побег «А», на междоузлии «б» материнского побега - боковой побег «Б» и т.д.
Признак «год» означает время от начала роста дерева, признак «бок/ось» принимает значение «0», если побег боковой, и «1», если он осевой.
Приставка «Log» перед кодом признака означает, что при анализе связей его значения были логарифмированы. Типы распределений были проверены при помощи критерия Колмогорова-Смирнова. Для сравнения распределений длин междоузлий на побеге их сумм были рассчитаны корреляционные отношения Пирсона, статистика Хотеллинга и коэффициент асимметрии побега.
Результаты. Побеги A. negundo разнообразны как по числу листьев, так и по длине междоузлий. 1-3-е междоузлие на побеге формирует почечные чешуи и их размеры очень малы и маловариабельны: от 0,2 до 1(3) мм. Четвертое междоузлие образовано катафиллами, его размеры варьируют от 1 до 34 мм. Начиная с пятого междоузлия, на побеге развиваются листья срединной формации. Средние по длине побеги имеют шесть пар настоящих листьев, из которых только пять крупных размеров. Побеги большей длины имеют до двадцати листьев. От 11 до 15 междоузлий относится к первому периоду роста, причем на 11-14-е междоузлие приходится минимум кривой длин междоузлий и переход ко второму периоду роста (рис. 1. А). ~
Большинство побегов состоят из 8-10 междоузлий. Коэффициент асимметрии для одноцикличных побегов вычислялся как отношение сумм длин междоузлий перед максимальным, считая от начала побега, к его окончанию, без самого наибольшего значения. Он имеет выраженное логнормальное распределение (рис. 1. Б). Асимметрия имеет большой разброс, но в целом длина правой ветви кривой превосходит длину левой.
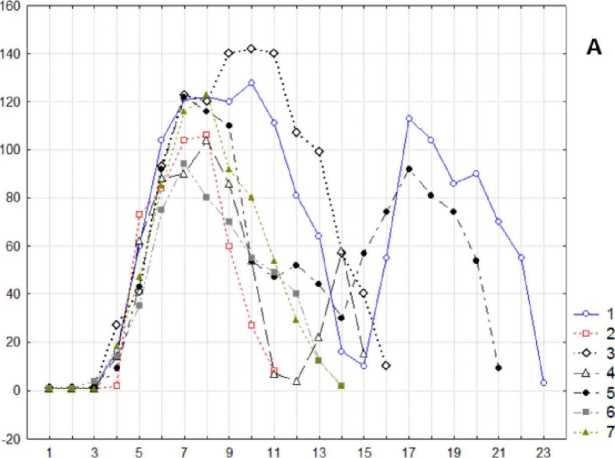
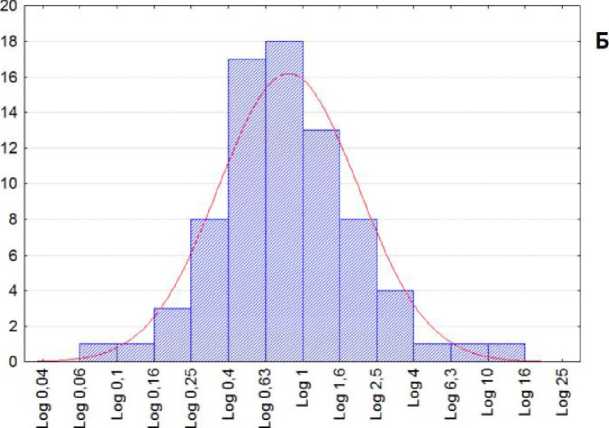
Рис. 1 . А. Изменения длин междоузлий на наиболее мощных побегах A. negundo; ось абсцисс - № листа, ось ординат - длина междоузлия, мм; Б. Гистограмма распределения логарифмов коэффициентов асимметрии на 86 побегах A. negundo общей группы. По оси абсцисс данные представлены в шкале логарифмов миллиметров. Применен модифицированный критерий Колмогорова - Смирнова для проверки на нормальность: Р = 0,9; размах выборки: 0,08 - 12,7; геометрическое среднее: 0,82; доверительный интервал для среднего: 0,68 - 1,00.
У побегов с меньшим количеством листьев на восходящую и нисходящую ветви кривой изменения длин междоузлий приходится примерно одинаковое количество узлов. Тогда как у побегов с большим количеством междоузлий на восходящую часть кривой приходится явно меньшее количество узлов.
Наиболее мощные оси первого и второго порядка, образующие скелетную часть кроны A. negundo, характеризуются в молодом генеративном состоянии некоторым разнообразием побегов, их составляющих: присутствуют как короткие (до 87 мм), менее облиственные, так и длинные побеги. У особей, победивших в конкурентной борьбе, процент коротких побегов в средней части стволов невелик, менее 10%.
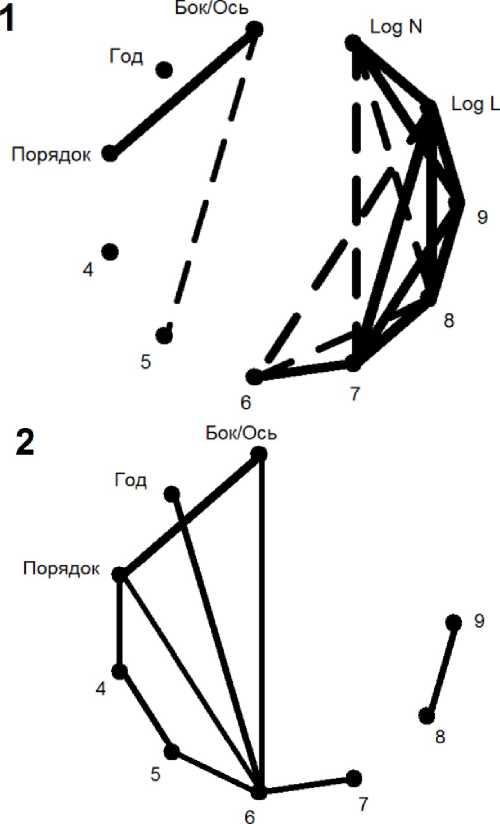
Рис. 2 . Диаграмма корреляционных плеяд (по В.П. Терентьеву) нижней части побега. Представлены выборочные (1) и частные (по признакам «Общая длина побега» и «Количество листьев на нем») выборочные (2) коэффициенты корреляции Пирсона для двух наборов признаков основного массива данных (86 побегов). На граф. 1 пунктир соответствует уровню корреляций выше 0,5, а сплошная линия - уровню выше 0,75. На граф. 2 сплошная линия соответствует уровню 0,5. Толщина линий, обозначающих связи между признаками, пропорциональна коэффициенту корреляции между ними.
Рис. 3 . Диаграмма корреляционных плеяд (по В.П. Терентьеву) верхней части побега. Обозначения аналогичны обозначениям на рис. 2.
Для выявления зависимости между длинами междоузлий, количества листьев на побеге и длин боковых побегов у осей разных порядков был проведён корреляционный анализ данных на основе метода корреляционных плеяд В.П. Терентьева. В анализ включены: длины междоузлий (1 - 9 и «а» - «е»), а также их последовательно накопленные суммы от соответствующего конца побега, длина побега, количество узлов, длины боковых побегов, год образования материнского побега, его порядок. В анализ не были включены длины междоузлий 1, 2, 3 начала побега из-за малого разброса: почти все значения были равны 1.
Диаграммы рис. 2.1 и 3.1 показывают сильную корреляцию длин междоузлий с признаком общая длина побега, а также с признаком количества листьев, нарастающую по мере удаления междоузлий от обоих концов побега. В эту систему связей также включены длины боковых побегов. После элиминации этих двух интегральных признаков при переходе к частным корреляциям (рис. 2.2 и 3.2) система связей распадается на корреляции средней силы (до 0,6; табл.1): между попарными длинами междоузлий, между связями «бок/ось - порядок» и между попарными последовательными связями длин боковых побегов.
Такое изменение характера связей между длинами последовательных междоузлий и выравнивание этих связей показывает, что изменение общей длины побега является функцией средних междоузлий. Крайние междоузлия «а», «б», «в» и «4», «5» не оказались связанными прямо пропорционально, то есть на уровне корреляций, с этой функцией, и последовательные корреляции между ними уменьшились мало, а местами даже увеличились.
Междоузлия «а» и «4» имеют особый статус. Их длины логарифмически нормально распределены (тест Колмогорова-Смирнова: р = 0,1; нормальность распределения для междоузлия «4» по тому же критерию так же не отвергается на уровне р = 0,09), они не проявляют корреляций с исследуемыми признаками, кроме как с длинами соседних междоузлий. У более удаленных от краев побега междоузлий «б-г» и «5-7» гипотезы как о нормальности, так и о равномерности распределений не отвергаются модифицированным критерием Колмогорова-Смирнова (р = 0,3 и р = 0,2, соответственно). Чем ближе к краям побега, тем своеобразнее каждое из междоузлий.
Междоузлие «6», «7», «8», «9» связаны с общей длиной побега, причем от «6» к «9» связь последовательно возрастает. Корреляция признака «число листьев» с длиной междоузлия «6» почти отсутствует. Например, связь междоузлий «6» и «8» транзитивно наследуется от связи с общей длиной побега.
Заметим, что между соседними междоузлиями присутствуют последовательная цепь частных корреляций как в начале, так и в конце побега. Междоузлие «а» сильно связано с междоузлием «б», которое отчётливо связано с междоузлием «в», при этом связь «а»-«в» очень слабая. Аналогичная структура связи выявляется и для последующих междоузлий. Похожее явление известно в исследованиях метамерной системы злаков. Так, в 2001 году С.А. Степанов обратил внимание на формирование корреляционных цепей в морфогенезе злаков, в том числе между метамерами побега (Степанов, 2001). В.В. Коробко (2007) наблюдала межметамерную синхронизацию роста стебля яровой пшеницы. «Скрытый» рост пятого междоузлия наблюдался под влагалищем четвертого листа. Пятый лист оказывал влияние на оба соседних с ним междоузлия. В связи с этим можно предположить, что выявленный эффект «цепи связей» у Л. negundo обусловлен влиянием донорно-акцепторных отношений листа с соседними междоузлиями.
В диаграмме частных корреляций выделяющиеся плеяды подтверждают связь между междоузлием «6» и признаками плеяды «порядок - бок/ось» и «год», а значит, являются отражением возраста побега (рис. 2). Это подтверждает необходимость учета возрастного состояния растения в выборке при анализе свойств побега. Отметим, что у верхнего конца побега связь междоузлий «б», «в» и других с плеядой «бок/ось - порядок» и «год» отсутствует, что, вероятно, отражает явление полярности, присущее побегу.
Длины боковых побегов не имеют сильной связи ни с междоузлиями на которых они развились, ни с другими междоузлиями (рис. 3). Полные корреляции колеблются от 0 до 0,51, а частные корреляции с элиминацией влияния признаков «длина побега» и «количество листьев» на нем не превосходят 0,3. Из этого следует, что длины боковых побегов слабо связаны с общей длинной их материнского побега.

Рис. 4 . Визуальное соответствие узлов на шести побегах A. negundo из основного массива данных.
В теории циклического старения и омоложения растений Н.П. Кренке особое внимание обращал на роль междоузлий концов побега. Эти междоузлия наиболее контрастно отражают процессы старения и омоложения побега, которые, протекая циклически в календарном времени, разбивают его на два внутренних времени.
На рис. 4 представлены шесть мощных побегов A. negundo, совмещенных по расположению на материнском побеге наиболее крупных боковых.
Хорошо видно совпадение размерных характеристик четырех верхних междоузлий: «а», «б», «в», «г». Поскольку междоузлие «а» заметно отличается от остальных по размеру, и, кроме того, выравнивать побеги для сравнения целесообразно по расположению наиболее крупных боковых. Заметим, что при таком сравнении сам эффект наложения основан на переходе от длин междоузлий к их накопленным суммам, которые имеют самостоятельный морфологический смысл. Рассмотрим суммы накопленных длин трех междоузлий: «б», «б+в», «б+в+г».
Дисперсии главных компонент для корреляционной матрицы, вычисленных по этим трем признакам для 86 побегов общего массива данных, относятся друг к другу примерно как 100:10:1, причем доля общей дисперсии первой главной компоненты превышает 90% (табл. 1). Такая масштабная разница в пропорции дисперсий главных компонент и лежит в основе эффекта совмещения междоузлий на рис. 4.
Таблица 1 Нагрузки главных компонент корреляционной матрицы
|
Признак |
ГК 1 |
ГК 2 |
ГКЗ |
|
б |
0,92 |
0,38 |
0,06 |
|
б+в |
0,99 |
-0,03 |
-0,13 |
|
б+в+г |
0,94 |
-0,34 |
0,08 |
|
Собственные числа КМ |
2,714 |
0,259 |
0,027 |
|
Доля в общей дисперсии |
90,5 |
8,6 |
0,9 |
Примечание. ГК - главные компоненты, КМ - корреляционная матрица.
Таблица 2
Корреляции первой главной компоненты с длинами междоузлий концов побега
|
Признак |
Корреляции |
Частные корреляции |
|
а |
-0,42 |
-0,41 |
|
б |
-0,92 |
-0,91 |
|
в |
-0,90 |
-0,87 |
|
г |
-0,65 |
-0,49 |
|
Д |
-0,44 |
-0,10 |
|
е |
-0,35 |
0,20 |
|
4 |
-0,03 |
0,02 |
|
5 |
-0,43 |
-0,28 |
|
6 |
-0,63 |
-0,42 |
|
Общая длина побега |
-0,52 |
- |
Первая главная компонента (ГК1) слабо коррелированна с общей длиной побега и с междоузлиями а, д, е и 4, 5, 6. Частные корреляции ГК1 и междоузлий д и е при элиминации влияния общей длины побега почти исчезли, что отражает их существенную связь с длиной побега. Междоузлия 4, 5, б менее зависимы от этой элиминации. Таким образом, вклады междоузлий в общую длину побега существенно различаются, а междоузлия верхнего конца побега обладают специфическими чертами.
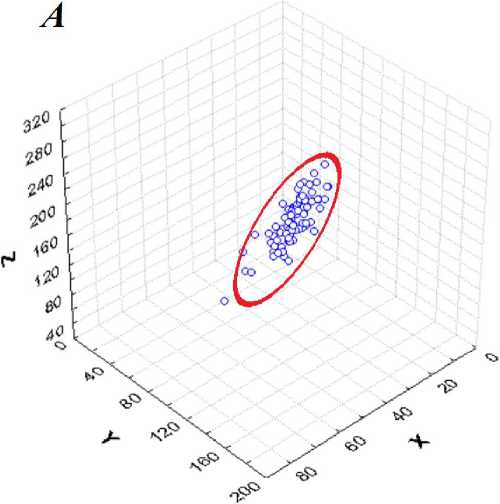
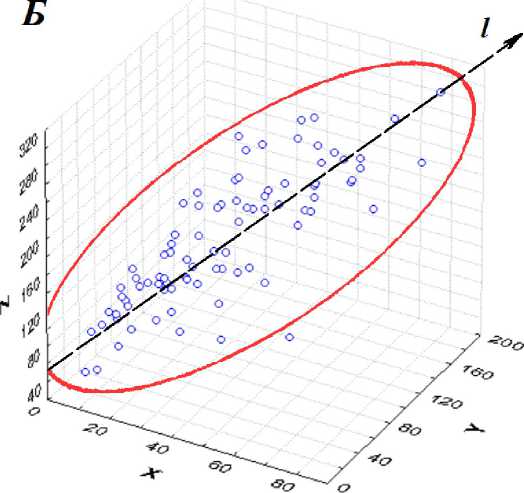
Рис. 5 . Трехмерные диаграммы рассеяния признаков: X - «б», ¥ - «б+в», Z-«б+в+г» - в плоскостях: А - 2-й и 3-й главной компоненты, Б - 1-й и 2-й главной компоненты. Штриховая линия / соответствует оси 1-й главной компоненты. Жирная линия соответствует 95%-ному нормальному эллипсоиду рассеяния.
Отметим, что здесь факторный анализ использован не для сокращения количества признаков, а выявления их структуры.
Факторный анализ ковариационной матрицы позволит установить роль главных компонент в реализации длин междоузлий на концах побега. Почти все точки трехмерной диаграммы рассеяния на рис. 5 накрываются трехмерным нормальным эллипсоидом, с доверительной вероятностью Р = 0,95. Нормальность распределений сумм междоузлий «б», «б+в», «б+в+г» не отвергалась тестом Колмогорова-Смирнова. Большая разница пропорций дисперсий главных компонент вызывает существенную вытянутость эллипсоида рассеяния вдоль его главной оси, параллельной первой главной компоненте. На рис. 5.А и 5.Б хорошо видна разница вкладов всех трех главных компонент ковариационной матрицы в общую дисперсию.
Рис. 6 . Диаграмма совместного прогноза рассеяния по трехмерному 95%-му нормальному эллипсоиду сумм длин междоузлий: А) «б», «б+в», «б+в+г»; / -линия выравнивания побегов по последнему узлу; «а» - «г» - междоузлия;
M[=34 , М2=93 , М3=160 - выборочные средние признаков «б», «б+в», «б+в+г»; пунктиром обозначен пример выявления совместного разброса междоузлий на гипотетическом побеге; 1, 2, 3 - проекции главного диаметра эллипсоида на оси признаков «б», «б+в», «б+в+г», соответственно; 4 -диапазон значений первой главной компоненты в третьей четверти эллипсоида рассеяния; Б) «4+5», «4+5+6», «4+5+6+7»; / - линия выравнивания побегов по третьему узлу; М^б? , М2=142, М3=215 - выборочные средние признаков «4+5», «4+5+6», «4+5+6+7»; 1, 2, 3 - проекции главного диаметра эллипсоида на оси признаков «4+5», «4+5+6», «4+5+6+7», соответственно.
Распределение вероятностей Р попадания в 3-хмерный нормальный эллипсоид рассеяния с уравнением описывается функцией
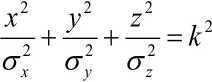
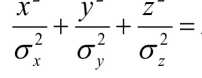
P(k) = ^"°’5р + ^e^dr^ = 2Ф(£) -1 - ^е"°’5р приведенной в учебнике Е.С. Венцель (1999), где (т^сг , На рис. 6 в одном масштабе представлены совместные диаграммы проекций трехмерного 95%-ного нормального эллипсоида рассеяния. Они представляют собой 95%-ные совместные доверительные области рассеяния трех узлов побегов массива данных для верхнего и нижнего концов побега. Диаграмма построена таким образом, что любой побег массива данных с 95%-ной вероятностью может быть представлен на ней так, как показано на рисунке. При этом каждый узел в начале (А) или в конце (Б) побега попадает в соответствующий эллипс. Ось / можно считать осью первой главной компоненты. Отрезки пересечения любой вертикальной прямой с эллипсами на диаграмме равны проекциям сечений эллипсоида рассеяния плоскостями, параллельными плоскости 2-ой и 3-ей главных компонент, на оси признаков «б», «б+в» и «б+в+г» (рис. б.А). То есть длины отрезков отражают вариации совместных частных распределений этих признаков при фиксированных уровнях 1 -й главной компоненты. Как видно из диаграммы, узлы на побеге, рассмотренные вместе, дают незначительные разбросы вокруг главных осей эллипсов, что свидетельствует о жесткой пропорциональности междоузлий у всех исследованных побегов. Важно, что распределения соответствующих узлов внутри эллипсов на диаграмме рис. 6 в данном случае наследуется от распределения точек внутри эллипсоида на рис. 5 и оказывается достаточно равномерным. Пропорция для средних на рис. б.А: Mi: М2 : М3=1 : 2,7 : 4,7. Все сказанное относится и к началу побега (рис. 6.Б) для междоузлий 4, 5, 6; пропорция для средних: ' М1:М2:Мз=1 : 2,1 : 3,2. Таким образом, диаграмма отрицает возможность произвольного соотношения длин междоузлий на побеге. Кроме того, выявленная устойчивость пропорций, несомненно, есть отражение программы развития побега. Сравнивая распределения диаграммы А и Б на рис. 6, отметим большую вариабельность накопленных сумм длин, а значит, и их отношений, в начале побега по сравнению с его концом. В литературе хорошо известны различия по времени и скорости роста начала и конца побега (Васильев и др., 1974). В нашем случае, это проявляется в разной толщине эллипсов и их отклонения от оси /. В частности, это означает асимметрию кривой Кренке. На рис. б.А был произвольно выбран небольшой диапазон значений первой главной компоненты, отмеченный фигурной скобкой на диаграмме. Группа побегов, попавших в этот диапазон, состояла из 26 побегов и обладала сходной длиной междоузлий (рис.7., табл. 3). В состав этой группы вошли растения трех различных популяций общего массива данных. А ■ 4. ■ 4+5, [ЩЩ| 4+5+6, s 4+5+6+7, И4+5+6+7+8 28 26 24 22 20 18 16 14 12 10 8 6 4 2 0 28 26 24 22 20 18 16 14 12 10 8 6 4 2 0 Рис. 7 . Совместные гистограммы накопленных сумм длин междоузлий в группе 26 побегов с начала (А) и с конца (Б) побега. Огибающие распределений признаков 4 и «а» имеют логнормальный тип. Анализ графика свидетельствует о разнице разбросов накопленных сумм длин междоузлий верхнего и нижнего конца побега: разброс сумм длин междоузлий в начале побега существенно (почти в два раза) больше, чем в конце. Эта «размазанность» сумм длин метамеров начала побега при достаточно узком диапазоне этого показателя в конце побега является выражением известного принципа неопределенности, например, между дисперсией и средним в статистике или координатой и временем положения частицы в квантовой механике. Это значит, что у большинства побегов абсолютные размеры метамеров начала и конца находятся в разных положениях всего диапазона изменения параметра I - первой главной компоненты. Речь идет о двойственности процессов омоложения и старения по Н.П. Кренке. Таблица 3 Некоторые описательные статистики крайних междоузлий 26 побегов ЬЧ Я я со О Я Й О S о о Я Я и 2 я 2 н я и ° н я 2 ® Б s Я Я Я Я ^ я ^ о « 5 2 Ри Ы) Ри о О —1 « О К! Я Я со О Я К О S о о Я Я Ри и Я ж Би 2 я 2 я Н Н и ° н я 2 s s s я я Я я ^ я ^ о « 5 ^ s я р о О 1—1 « О б 49,54 10,15 0,20 0,03 4 15,4 8,5 0,55 0,29 в 78,08 9,44 0,12 0,03 5 61,0 22,7 0,37 0,26 г 89,31 24,82 0,28 0,56* 6 96,1 27,9 0,29 0,52* Д 89,19 40,05 0,45 0,71* 7 97,5 30,3 0,31 0,78* е 72,42 47,88 0,66 0,85* 8 85,2 34,4 0,40 0,88* Примечание *- значимые корреляции на уровне Р = 0,05. В табл. 3 приведены сравнительные характеристики самих длин междоузлий (в отличие от их накопленных сумм), которыми чаще оперируют в ботанике. Увеличение коэффициента вариации от «в» к «е» и от «6» к «8» связано с изменением структуры распределения этих длин междоузлий и соответствует резкому увеличению коэффициенту корреляции с общей длиной побега. Подчеркнем, что выявленная схожесть соотношений междоузлий концов побега независимо от года, места происхождения (европейская часть средней полосы России) и местоположения самого побега в кроне, является, по-видимому, свойством побегов данного вида. Вопрос, является ли это свойство характеристическим, остается открытым. Заключение. В отличие от других жизненных форм деревья обладают сравнительно небольшим разнообразием вариантов побегов в пределах вида. Так, травянистые растения обладают значительно большим сочетанием длин междоузлий и развитием листовых - 156- пластинок и почек. На побег дерева ложится большая программная нагрузка, состоящая в передаче и хранении информации разного содержания от материнского побега к «детям», внукам и так далее. В частности, эта информация касается пространственного расположения и реакции на окружающую среду на всех уровнях от особи до конкретных соседних побеговых систем. Проблема хранения, передачи и использования этой информации определяет жесткую структуру побега на дереве, которая проявляется морфологически: во времени - более жестким и структурированным годовым циклом, в пространстве - в последовательной зональности, связанной с программой развития побега. На максимально развитых побегах виргинильного и молодого генеративного состояния A. negundo морфофизиологически выделяются пять групп междоузлий, отражающих динамические стадии развития побега. Из них крайние верхнее и нижнее междоузлия соответствуют рождению и завершению роста побега. Междоузлия, следующие за первыми от начала пробега, соответствуют стадии наиболее интенсивного ускорения роста побега и морфологически связаны с материнским. За ними следует зона междоузлий средней части побега, наиболее тесно связанных с общей его длиной и количеством листьев. Наконец, нисходящая часть кривой на диаграмме длин междоузлий соответствует зоне заложения основных боковых побегов и не коррелирует с общей длиной и количеством листьев на побеге. Анализ структуры главных компонент последовательности концевых междоузлий и их накопленных сумм длин от концов побега выявляет жесткие ограничения на соотношения длин этих междоузлий на побеге. Эти ограничения приводят к большой схожести разных побегов по распределению крайних междоузлий. Эта схожесть наблюдается у побегов различного года, места происхождения и местоположения самого побега в кроне, имея, по-видимому, программный характер. Антонова И.С. К вопросу о зональности на примере побегов Acer negundo L. / И.С. Антонова, В.А. Барт // Вести. ТвГУ. Сер.: Биология и экология. 2015. № 4. С. 143-159.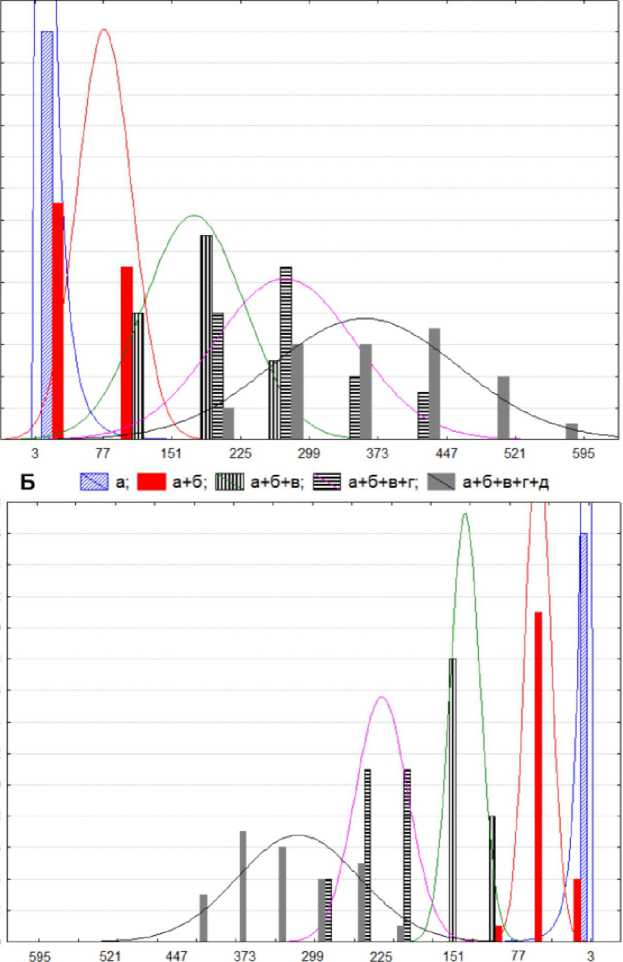
Список литературы К вопросу о зональности побега на примере побегов Acer negundo L.
- Антонова И.С., Азова О.В. 1999. Архитектурные модели кроны древесных растений//Бот. журн. Т. 84. № 3. С. 10-28.
- Антонова И.С., Гниловская А.А. 2013. Побеговые системы кроны Acer negundo L. (Aceraceae) в разных возрастных состояниях//Бот. журн. Т. 98. № 1. С.53-68.
- Антонова И.С., Николаева Н.В. 2004. Элементарная побеговая система как единица структуры кроны древесных растений умеренной зоны//Материалы X Школы по теоретической морфологии растений. Конструкционные единицы в морфологии растений (Киров, 2-8 мая 2004 года). Киров: Издательство Вятского государственного гуманитарного университета. С. 10-12.
- Антонова И.С., Фатьянова Е.В., Зайцева Ю.В., Гниловская А.А. 2012. Мультимасштабность побеговых систем некоторых деревьев умеренной зоны (разнообразие, классификация, терминология)//Актуальные проблемы современной биоморфологии/Под ред. Н.П. Савиных. Киров: Изд-во ООО «Радуга-ПРЕСС». С. 390-402.
- Аренс Х., Лейтер Ю. 1985. Многомерный дисперсионный анализ. М.: Финансы и статистика. 230 с.
- Барт А.Г. 2003. Анализ медико-биологических систем. Метод частично обратных функций. СПб.: Изд-во СПбГУ. 280 с.
- Васильев Б.Р., Звонцова Н.А., Шмидт В.М. 1974. Математический анализ роста листьев Nicotiana rustica L. и Zea mays L.//Бот.журн. Т. 59. № 5. С.655-659.
- Вентцель Е.С. 1999. Теория вероятностей: Учеб. для вузов./6-е изд. стер. М.: Высш. шк. 576 c.
- Ито К. 1960. Вероятностные процессы. Вып.1. М.: ИЛ. 134 с.
- Колмогоров А.Н. 1936. Основные понятия теории вероятностей. М.-Л.: ОНТИ. 80 с.
- Коробко В.В. 2007. Метамерные особенности роста и развития междоузлий стебля яровой пшеницы/Автореферат. Саратов. 28 с.
- Кренке Н.П. 2015. Теория циклического старения и омоложения растений и ее практическое применение. М.: Книга по требованию. 138 с.
- Сабинин Д.А. 1963. Физиология развития растений. М.: Наука. 196 с.
- Савинов И.П., Васильев Б.Р., Шмидт В.М. 1976. Сравнение логистической функции с функцией Гомпертца и вопросы прогнозирования ростовых процессов//Вестн. Ленингр.ун-та. № 9. С. 63-70.
- Степанов С.А. 2001. Структурные и функциональные аспекты межметамерных отношений в онтогенезе побега яровой пшеницы. М. 38 с.
- Фатьянова Е.В., Антонова И.С. 2010. О разнообразии почек систем побегов заполнения кроны хурмы кавказской (Diospyros lotus L.)//Бюл. МОИП. Отд. Биол. Т. 115. Вып. 2. С. 49-58.
- Barthelemy D, Caraglio Y. 2007. Plant architecture: a dynamic, multilevel and comprehensive approach to plant form, structure and ontogeny//Ann. Bot. № 99. Р. 375-407.
- Chaubert-Pereira F., Guédon Y., Lavergne C., Trottier C. 2010. Markov and semi-Markov switching linear mixed models used to identify forest tree growth components//Biometrics. № 66 (3). Р. 753-762.
- Maillette L. 1987. Effects of bud demography and elongation patterns on Betula cordifolia near the tree line//Ecology. № 68. Р. 1251-1261.
- Maillette L. 1982. Structural Dynamics of Silver Birch II. A Matrix Model of the Bud Population//Journal of Applied Ecology. V. 82. Р. 219-238.
- Prusinkiewicz P., Lindenmayer A. 2012. The Algorithmic Beauty of Plants. Springer Science & Business Media. 240 p.
- Wilson B.F. 1989. Tree branches as population of twigs//Can. J. Bot. № 67. Р. 434-442.


