К вопросу об отличиях в поведении решений линейного и нелинейного уравнений теплопроводности

Известно (см., например, серию работ [1–5]), что нелинейные уравнения теплопроводности и некоторые другие нелинейные уравнения в частных производных описывают режимы, значительно отличающиеся от тех режимов, которые наблюдаются, если используется линейная модель процесса. ^асто в случае нелинейных моделей наблюдаются так называемые катастрофы, при которых решение неограниченно возрастает за конечный промежуток времени [1].

В данной работе приведены некоторые точные решения для линейного и нелинейного уравнений теплопроводности [1], которые являются хорошей иллюстрацией описанной выше проблемы. Полученные одним и тем же геометрическим методом [6, 7] решения имеют одинаковые поверхности уровня, но их поведение значительно отличается, так как сами решения удовлетворяют разным обыкновенным дифференциальным уравнениям (ОДУ), к которым сведены первоначальные уравнения теплопроводности. Аналогично при рассмотрении характеристик уравнений отличие в представлении их решений связано с отличием ОДУ, которые задают условия совместности для получения решения вдоль характеристик. Вид выписанных явно точных решений делает наглядными их отличия и позволяет легко увидеть, почему в нелинейном случае наблюдается обострение, а в линейном случае обострение отсутствует. Приводятся картины течений нелинейного уравнения теплопроводности в зависимости от параметров задачи, которые показывают, как можно отодвинуть по времени момент обострения в решении или, переключаясь на другое решение при подходе к обострению, избежать катастрофы.

Сведение линейного и нелинейного уравнения теплопроводности к обыкновенным дифференциальным уравнениям

Будем рассматривать два (линейное и нелинейное) уравнения теплопроводности [1]

ut = kuxx + qu, k = const, q = const.(1)

ut = kuxx + qu -au3, a = const.(2)

Здесь и далее нижние индексы указывают на независимую переменную, по которой вычисляется производная.

В уравнениях (1) и (2) сделаем замену [6] u = Q_x , тогда получим уравнения

Qxt = kQxxx + qQx,(3)

Qxt = kQxxx + qQx - aQx3.(4)

Считаем, что существует такая система координат [6, 7], в которой функция Q зависит от одной независимой переменной: Q = Q(у(x, t)), тогда у(x, t) = const - поверхность уровня решения Q(x, t). В этой системе координат уравнения (3) и (4) соответственно имеют вид kQ Wx+ Q ( у^у,+ 3kVxVxx)+Q (у+ k^xxx+ qVx)=о,               (5)

⁽ kQ - a ^Q у + ^{Q (} — W x W t ^{+ 3} k W x W xx ) ^{+ Q ( -} W xt ⁺ k W xxx ⁺ q W x ) = 0.            ⁽⁶⁾

Здесь и далее штрих ( ' ) указывает на производную по переменной у . Сравнивая (5) и (6), замечаем, что для определения функции у ( x , t ) имеем одни и те же уравнения, если положим, что

¥ x * 0 [6, 7]

^{- у} , ^{+ 3 k y} xx = f ( у ) ^-¥ xt ⁺ ^ xx ⁺ W x = f ( у )

¥х         1     ,           ^x            ¹    "

Здесь f1 (у), f 2 (у) — произвольные функции. Будем устанавливать, когда система уравнений (7) совместна. Из первого уравнения системы ¥xx = (у, + /1¥x')/(3к). Продифференцируем это соот ношение по переменной x и полученную производную ¥xxx подставим во второе уравнение сис темы. Разрешив полученное соотношение относительно производной ¥xt, имеем у + f ух        3              1              1     1 „2 3

¥xx = t * x , ¥xt = тq¥x + fз¥x + туf1¥x¥t, fз = уf. + тгf. -уfг-

3 к            X              3 к              X     3 кX

Соотношения (8) будут задавать производные второго порядка одной и той же функции, если смешанные производные равны (¥xxt = ¥xtx). Это условие выполняется, когда у« = 3q¥t + f^¥t + 3fз¥t¥xX + fу4, f4 = хflf3+ 3f(9)

X 3 к

Чтобы все полученные вторые производные были производными одной функции уxt, их смешанные производные должны быть равны. Требуем, чтобы ¥xtt = ¥ttx. Условие будет выпол- няться, если

6 f уу Х + 6 f з ¥ t ² + 3 к ( f 4 + f i f 4 / к ) у 4 = 0.                      (10)

Замечаем, что если f ₃ = 0 , соотношение (10) обращается в тождество. Полученные результаты приводят к следующему утверждению:

Утверждение 1. Система (7) совместна, если вторые производные функции у(x, t) определяются. из соотношений (8), (9) и fх = f1 /3 + Xf1X/(9к), f(у) - произвольная функция. В этом случае уравнения (5), (6) имеют вид соответственно kQ + Qf1 + Q[f1/3 + XfX/(9к)] = 0; (kQ -aQ3) + Q f. + Q[f /3 + XfX/(9к)] = 0.

Если f 3 * 0, то, выписав дифференциальные следствия соотношения (10) и подставив в полученные выражения вторые производные из (8), (9), получим, что ¥ _x = д 1 ( у ), у , = g^ у ). Потребовав равенства смешанных производных, будем иметь g^ у ) = Cg 1 ( у ), C = const. Тогда справедливо

Утверждение 2. Если f ₃ * 0 , то у = у ( ax + bt ), a = const , b = const . Тогда, так как u = Q_x = Q ( у ))у_х ( у ) , то u = u ( ax + bt ) и уравнения (1) и (2) имеют вид соответственно - bu z + ка ^X u zz + qu = 0, - bu z + ка ^X u zz + qu - a u ³ = 0, z = ax + bt .

Отыскание поверхностей уровня для уравнений теплопроводности

Положим, что произвольное f 1 = const и f _X = X f 1^X /(9 к ) = const. Тогда условие (10) выполняется. Из соотношения (9) находим у ₁ , считая, что x - параметр. Предварительно полагая, что у , * 0, запишем (9) в виде (1/ у _г ) _t + 1,5 q(1/ у₄ ) = f 1 /(3 к ). Решаем это линейное уравнение и получаем, что у , = 1,5 qC ( x )exp(3 qt /X)/[1 - f 1 C ( x )exp(3 qt )/(3 к )]. Затем из второго соотношения (8) определяем ¥ _x . Получаем, что

Математика

V x = C x exp(3 qt / 2) /[1 - fC ( x ) exp(3 qt / 2)/(3 k )].

Требуя тождественного выполнения первого соотношения (8), приходим к уравнению для определения C ( x ): C_xx = qC /(2 k ). Отсюда C ( x ) = A 1 exp[ ± x4q /(2 k )] + A ₂exp[ + x^q /(2 k )]. Здесь

A1 = const, A2 = const. Далее положим, что A1 = 1, A2 = 0 и выпишем для этого случая оконча тельный вид Vt и Vx

3 q exp [(3 qt /2) ± x-^q /(2 k ) ] / 2          ± ^/ q /(2 k ) exp [(3 qt /2) ± x4q /(2 k ) ]

t   1 - f 1 exp[(3 qt /2) ± x^/q /(2 k )]/(3 k )’ ^ x 1 - f 1 exp[(3 qt /2) ± x^q /(2 k )]/(3 k )

В выражении для V _x знак перед числителем выражения совпадает со знаком в показателе степени экспоненты. Далее, находим, что поверхность уровня в этом случае имеет вид

V = - 3 k ln{1 - f , exp [(3 qt / 2) ± x^q /(2 k ) ]/(3 k )}/ f 1 .                     (11)

Положим f ₂ = 0. Тогда f , ( v ) = 3 k /(2 v + v o ), V o = const (см. утверждение 1). Требуем далее, чтобы вторые производные функции v ( x , t ) удовлетворяли условиям (8), (9). Решая уравнение

(9) и второе уравнение из (8) и считая при этом, что x - параметр, получаем, что

V t = 42V + V o [ M ( x ) + 3 q 4W /2], V x = N ( x )^2 V + V o exp(3 qt /2).

Требуя тождественного выполнения первого условия (8), окончательно получаем

2 k ²

V = —

q

qq"    ( 3       [q" ) M

±. —exp -qt ± x.—--

V 2 k ( 2     П k J 3 k

V o

2 ,

M = const,

V o = const.

Заметим, что знаки перед экспонентой и в показателе степени экспоненты совпадают.

Из условия f ₂ = 0 следует, что V _t - k V xx - q V = A = const. Нетрудно проверить, что если V o = 4 M ² /(9 q ² ), то подстановка функции v ( x , t ) из (2) в уравнение (1) дает A = 0. Итак, имеем

Следствие 1. Решение u ( x , t ) = (2 k ² / q ²){ ± 4q /(2 k )exp[3 qt /2 ± x4q /(2 k )] - M /(3 k )} ² - V o /2

линейного дифференциального уравнения u_t = ku xx + qu + C, где M = const , V o = const , C = C ( q , M , v _o ) , является поверхностью уровня уравнения (2).

Следствие 2. Решение u ( x , t ) = (2 k ² / q ²){ ± 4q /(2 k ) exp[3 qt /2 ± x4q /(2 k ) ] - M /(3 k )} ² - V o /2 линейного дифференциального уравнения (1) является поверхностью уровня уравнения (2), если V o = 4 M 2 /(9q ² ) .

Положим, что f2 = aQ 2 (v) , тогда согласно утверждению 1 система уравнений (7) совмест- на, если f'/3 + 2 f12/(9 k) = f2 = aQ'2.

С другой стороны, уравнение (6) в этом случае будет иметь вид kQ + Q f 1 = 0. Выражая отсюда f. и подставляя полученное значение в (13), приходим к зависимости

Q Q - 5 Q ²/3 + 3 a Q ² Q ² / k = 0.

Решая это уравнение, получаем частное решение Q = + V 2 k/ a (3 v + V ₀), где V ₀ = const. Далее из (13) определяем, что f. = 6 k /(3 v - V ₀) • Требуем, чтобы выполнялись соотношения (8), (9). В результате окончательно получаем, что

V = -

- — exp 3 3 q

1 qt ±x

-i 3

- c

-

V

- , c = const. 3

Точные решения уравнений теплопроводности

Определяем Q ( v ) из уравнений (случай f. = const)

kQ + Qf1 + Q [ f 1 /3 + 2 f ² /(9 k )] = 0 ; ( kQ - a Q ³) + Q f , + Q [ f/3 + 2 f 12 /(9 k )] = 0.

Решая линейное уравнение для Q ( v ) , находим, что

Q = C ₁exp[ - f y /(3 k )] + C ₂exp[ - 2 f y /(3 k )], C ₁ = const, C ₂ = const.

Учитывая, что решение уравнения (1) u = Q x = Q y _x , получаем

± V q /(2 k )exp[3 qt /2 ± xdq /(2 k )]

u = 1-^(3:x^)]/(3k) !C'exp["f У/(3k)] + C2exp[-2У/(3k)]!-

Подставив сюда выражение для у из (11), имеем

q u = ± exp

V 2 k ^P

1 ⁺ C 2

1 —¹ exp 3 k

.

Решаем нелинейное уравнение для Q( у ). Полагаем, что Q = p( у ), а затем полагаем, что p = r ( p ). В результате приходим к уравнению krr_p + f . r = a p ³ - 2 f ² p /(9 k ). Находим частное решение данного уравнения вида r = ap ² + bp , где a = const, b = const. Получаем, что a = ± ^j a /(2 k ), b = f _ /(3 k ). Возвращаясь к первоначальному уравнению, имеем

Q = -

f /(3 k )

± -7 a /(2 k ) - C exp[ f y /(3 k )]

, C = const.

Учитывая, что решение уравнения (2) u = Q_x = Q y _x , выпишем окончательно решение уравнения (2)

u =

± [ f 1 /(3 k )] ^qT a exp[3 qt / 2 ± x^q /(2 k ) ] C = ± C

1 - C ₀ - [ f ₍/(3 k )]exp[3 qt /2 ± x^q /(2 k )]           ⁰

Здесь знак числителя не зависит от знака в показателе экспоненты, то есть фактически ется четыре решения

име-

[ f /(3 k )] J q / a exp[3 qt /2 + xdq /(2 k ) ] u =    -                                     , u =

1 - C ₀ - [ f ₍/(3 k )]exp[3 qt /2 ± x^/q /(2 k ) ]

u=

[ f ! /(3 k )] ^q / a exp[3 qt /2 - x^q /(2 k ) ]

- C о - [ f , /(3 k )]exp[3 qt /2 ± x,/q /(2 k )], u =

- [ f₁ /(3 k )] ^q / a exp[3 qt /2 + x^q /(2 k ) ] 1 - C ₀ - [ f _ /(3 k )] exp[3 qt /2 ± x^q /(2 k ) ],

- [ f , /(3 k )] JqT a exp[3 qt /2 - x^q /(2 k ) ]

1 - C ₀ - [ f , /(3 k )] exp[3 qt /2 ± x^q /(2 k ) ]

''

Для случая, когда f 2 = 0 уравнение (5) имеет вид Q + 3 Q /(2 у + y _o ) = 0. Решая это уравнение, определяем, что Q = C ₁ - C ₂ /^2 y + y o , C ₁ = const, C ₂ = const. Тогда окончательно получаем, учитывая (12), что

2 k 3    , u = — C1 exp —qt ± x.

q

exp

M

- 3 k

^^^^^^^s

(3      fq")

^C 2 ^ex p - qt ± ^x^ — •

Если f 2 = 0, то уравнение (6) имеет вид (Q - aQ / k) + 3Q /(2y + yo) = 0. Выпишем част ное решение этого уравнения: Q =±V2k/ a[1/(2у + yo)]. Соответствующее решение уравнения

• (6)    будет иметь вид

  q 21к    ( 3       qq" )    qq"    ( 3       qq" ) M

  ^u = Ml a ^exp [ i qt ± ^x V 5 k J[ ±/2 k ^exp [ 5 qt ± d 2f_k J - 5 k

  
  
  
  
  
  
  
  

Если поверхность уровня определяется выражением (14), решение уравнения (2) имеет вид u =± ^q/ a exp[3 qt /2 ± x-^q /(2 k )]{exp[3 qt /2 ± x^q /(2 k )] - c } ' , c = const. (18)

Здесь знак перед выражением для u может не совпадать со знаком в показателе экспоненты (имеем, фактически, четыре решения).

Другой подход к изучению поведения решений нелинейного уравнения теплопроводности

Покажем, что характеристиками уравнений (1) и (2) являются линии t = const .

Чтобы доказать это утверждение, в уравнении (2) перейдем от функции u ( x , t ) к функции t ( u , x ) [8]. Получим

Математика

t 2 + k ( t u t xx - 2 t_xt_ut_xu + t x t_uu ) - ( qu - a u ³ ) t 3 = 0.                       (19)

В уравнении (19) сделаем замену независимых переменных u - v ( x ) = j , x = п : j ^{+ k [} t j ⁽ t nn - ² t ^n ^ x ⁺ Ч Ф х - t ^ ^ xx ) - ² t j ⁽ t n - t j ^V x ⁾⁽ Чп - Ч Ф ) ⁺ t j ⁽ t n - 4^V x ^{) 2 ]} - [ q( j + v ) - a ( j + v ) ³ ] t j = 0.

Полагая, что j = const - характеристика уравнения (19), выпишем выражение перед производной tj и приравняем его нулю. Получим, что tn = 0. Отсюда следует, что на характеристике j = const имеем t = const. Тогда, чтобы уравнение (19) имело решение, вдоль характеристики должно выполняться условие совместности tj - ktjvxx - [q(j + V) - a(j + v)3]tj = 0. Решая это ОДУ, в случае, когда a = 0 (уравнение (1)), и заменяя j + v = u, получаем, что вдоль характери- стики t = const должно выполняться соотношение u (t, x) = {w0( t) + c 0( t )sin[±( x + c1 (t)) ^qI k ]}/q, c0 (t) = const, w0 (t) = const, c1 (t) = const.(20)

Подробнее остановимся на решении уравнения (2). Выпишем вид уравнения, считая, что x(u, t) - независимая переменная xtx2 - kxuu + (qu - au3)x3 = 0.(21)

Когда a Ф 0, требуя выполнения вдоль характеристики t = const условия совместности, приходим к выражению x = c1 ± j /4       du          =.

4au /(4 k ) - qu /(4 k ) + w ₀ u + c ₀

Здесь, вообще говоря, можно положить c 1 = c 1 ( t ), c ₂ = c ₂ ( t ), w ₀ = w ₀ ( t ) и, подставляя полученное выражение в уравнение (21), получить соотношения для определения неизвестных функций c 1 = c 1 ( t ), c ₂ = c ₂ ( t ), w ₀ = w ₀ ( t ). Чтобы представить в этом случае характер изменения интересующей нас функции u ( x , t ), преобразуем выражение под знаком корня в интеграле (22):

a u⁴ /(4 k ) - qu ² /(4 k ) + w ₀ u + c ₀ = [ a /(4 k )][ u ² + 2 a ( t ) u - ( q I a - 2 a ² ( t ) - b ( t ))][ u ² - 2 a ( t ) u

- ( q / a - 2 a ² ( t ) + b ( t ))]

и таким образом вычисление интеграла (22) приведем к выражению его через эллиптический интеграл первого рода, обратной функцией которого является функция Вейерштрасса [9]. Следовательно вдоль любой характеристики t = const имеем u ( x , t ) = p ( x ) ( p ( x ) - функция Вейерштрасса). Известно также [10], что функция Вейерштрасса имеет полюсы, приближение к которым, очевидно, будет приводить к обострению в решении, что не наблюдается в решении (20) линейного уравнения (1).

Заключение

Из полученных решений уравнения (2) следует, что катастрофа в процессах, которые описываются данным уравнением, возникает тогда, когда знаменатель решения (а он присутствует в решениях нелинейного уравнения (15)-(18) и у функции Вейерштрасса) стремится к нулю.

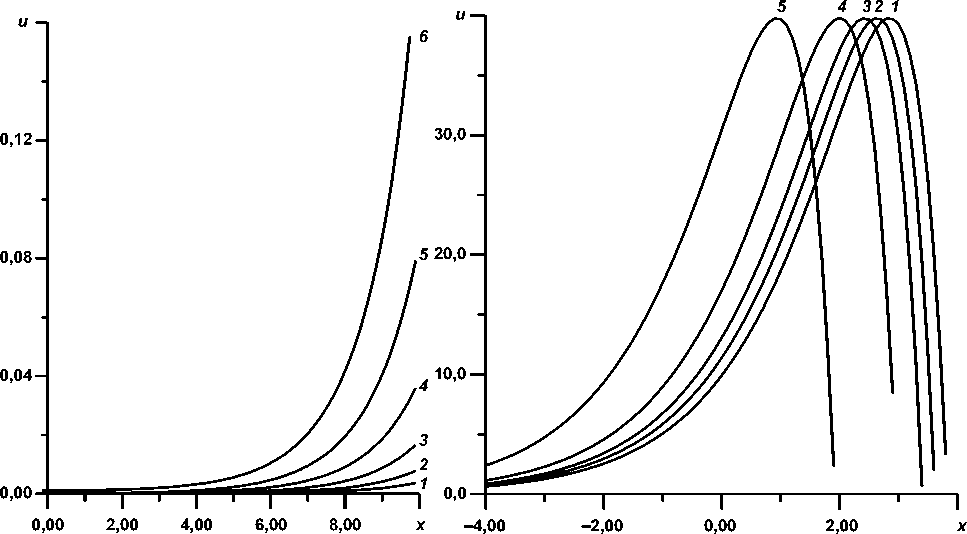
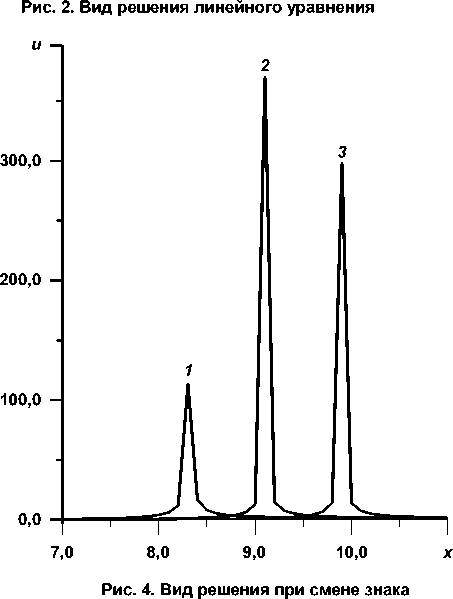
На рис. 1 показано поведение решения нелинейного уравнения в зависимости от времени ( 1 : t = 0; 2 : t = 0,5; 3 : t = 1; 4 : t = 1,5; 5 : t = 2; 6 : t = 2,5). На рис. 2 имеем вид решения в зависимости от времени для линейного уравнения ( 1 : t = 0; 2 : t = 0,1; 3 : t = 0,5; 4 : t = 1; 5 : t = 1,5).

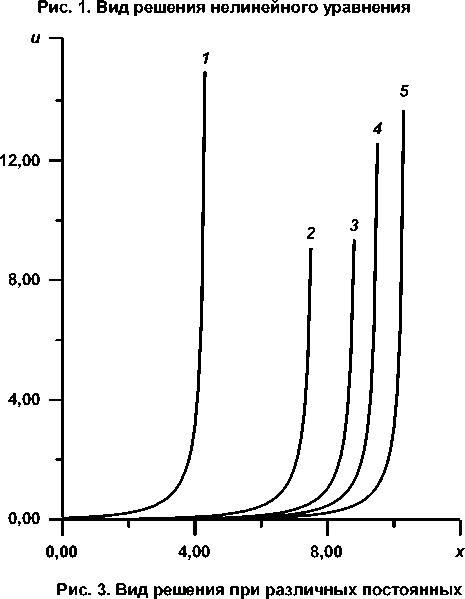
В выражениях (15), (17), (18) сразу виден управляющий параметр, выбор которого позволяет, по крайней мере, отодвинуть катастрофу в случае нелинейного уравнения - это произвольная постоянная в знаменателе решения нелинейного уравнения (см. рис. 3, вид u ( x , t ) для разных произвольных постоянных c в знаменателе решения при t = 1 ( 1 : c = 100; 2 : c = 1000; 3 : c = 2500; 4 : c = 4000; 5 : c = 7000).

Величина произвольной постоянной в знаменателе связана со значением решения в точке { x = 0, t = 0}. Так, в решении (18) c = [ ± 4q / a - u (0,0)]/ u (0,0). Если u (0,0) = + ^q / a , то c = 0 и

Рубина Л.И., К вопросу об отличиях в поведении решений Ульянов О.Н. линейного и нелинейного уравнений теплопроводности и ( x , t ) = const = + д/ q I a . Катастрофы удастся избежать также, если при стремлении знаменателя выражения к нулю сменить знак в числителе на противоположный (рис. 4, вид решения u ( x , t ) в случае задания разных произвольных постоянных c в знаменателе решения, 1 : c = 1600; 2 : c = 2800; 3 : c = 4900). Здесь возрастающие ветви решений получены, когда перед выражением (15) знак плюс, а убывающие участки решений получены, когда перед выражением (15) задавался знак минус (см. (16)). При каждом заданном значении и (0,0) увеличение времени процесса ведет к приближению катастрофы (рис. 1, сравните с поведением решения в зависимости от времени в случае линейного уравнения рис. 2).

Математика

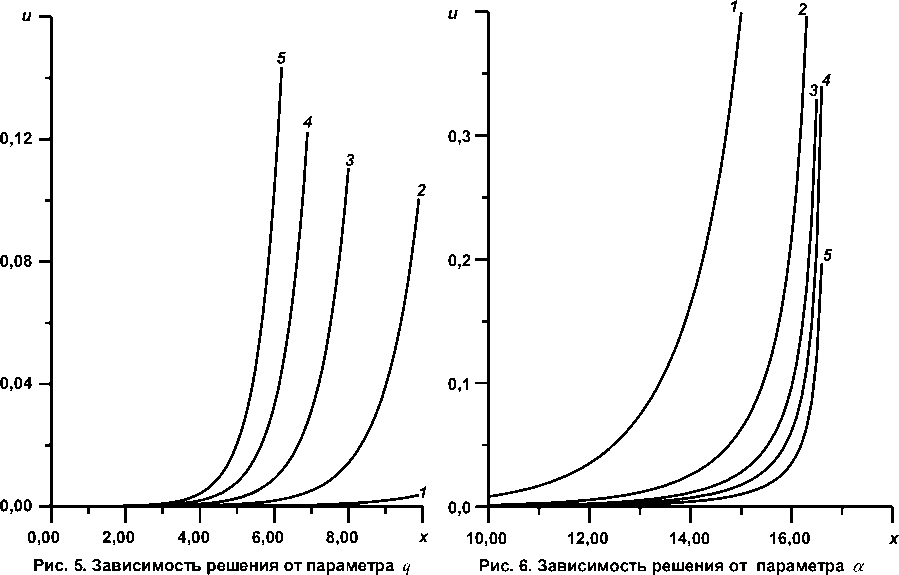
На рис. 5 показана зависимость решения от параметра q . Увеличение этого параметра приближает катастрофу ( 1 : q = 1; 2 : q = 2; 3 : q = 3; 4 : q = 4; 5 : q = 5). Изменение параметра α слабо влияет на решение, но большие его значения заметно отодвигают катастрофу (см. рис. 6; 1 : α = 1; 2 : α = 40; 3 : α = 200; 4 : α = 500; 5 : α = 1500).