К вопросу оценки напряжений в контактной зоне при резании

Введение. Тепловое состояние твердосплавного режущего инструмента на форсированных режимах резания в конечном итоге определяет работоспособность инструмента, а также качество изделий и производительность процесса обработки. (В данном случае речь идёт об обработке материалов, относящихся к группе труднообрабатываемых: жаропрочные стали и сплавы, титановые сплавы, композиционные материалы и др.)

Известные схемы расчёта температур в зоне резания [1—9] базируются на учёте тепловых потоков и температур, возникающих в зоне деформации и на контактных площадках инструмента. Для соответствующих вычислений необходимо знать касательные напряжения на передней (τ _пп ) задней (τ _зп ) поверхностях инструмента и напряжение (τ_φ ) плоскости сдвига.

Анализ известных зависимостей для определения напряжений в зоне резания.

В табл. 1 представлены формулы для расчёта касательных напряжений сдвига (τ_φ) на передней (τ _пп ) задней (τ _зп ) поверхностях инструмента. Данные по оценке напряжений и деформаций собраны из исследований по обработке материалов резанием [1—16], с использованием подходов, принятых в обработке металлов давлением [17—23].

Данные блока А табл. 1 по оценке касательных напряжений τφ плоскости сдвига можно разделить на четыре группы. Учитываются:

• —    механические свойства обрабатываемых материалов (№ п/п 1—10);

— уравнение энергетического (теплового) баланса зоны резания (№ п/п 11—15);

• —    влияние степени деформации (относительного сдвига) ε на напряжения τ_φ (№ п/п 16—18);

• —    совместное влияние деформаций е , скорости деформаций е температуры Т на напряжения τ_φ (№ п/п 19–23).

Касательные напряжения τ _пп на передней поверхности (блок Б табл. 1) и τ _зп на задней поверхности (блок В табл. 1) можно:

• —    рассчитывать, зная механические свойства обрабатываемых материалов а в ( S_b = а _в ( 1 + 5 ) , табл. 1, № п/п 24, 26—28, 31, 34);

• —    принять зависящими от напряжения сдвига τ_φ табл. 1, № п/п 29, 30, 32, 33).

1

2

3

4

12

.     cos ( ф - у + p )

т „ = R ■ sin ф-- —7---- L

^ф             ab ■ cos ( ф - y )

R — сила стружкообразования; φ и μ углы сдвига и трения на передней поверхности; α — толщина среза

[12]

13

.     cos ( ф - Y + p )

т „ = P ■ sin ф--; ^ф z         ab ■ cos ( p - y )

tgp = tg ( ш + у ) ; tgw = P_y/P_z

P_z и P_y тангенциальная и радиальная составляющие силы резания; ω угол действия

[13]

14

P_z ■ sinф - ^т ф =

"f      P     Pf 1 )"

1 - sin у + - y ■ cosy — [ V        P z       ^J V k ^J]

ab

cos ( ф - у ) cosγ

k_a — коэффициент утолщения стружки

[5]

15

P ■ sinф - V P 2 + P ² ■ s ⁱⁿ Ф ■ ^тф =              ab y       ■ ^s n ^ф ■

tgф = /^ФУ .

k - sin у a

P_х — осевая составляющая силы резания

[8]

16

^т ф = ^AE m .

ε — относительный сдвиг; A — предел текучести на сдвиг при e — 1, m — константа

[12]

17

⁰ s = a_E . i ■ ^E n ; ^т ф = ^0,577 - а_Е . 1 ■ ^E n

ε — относительный сдвиг (степень деформации) течения; a_E = ₁ — напряжение течения при e — 1,

n — 0,196 — для углеродистых сталей; n — 0,37 —

для нержавеющих сталей; n — 0,128 — для титано

вых сплавов

[19]

18

a s = ( 1,83 ■ a в + 4 ) . e n ; т_ф — 0,577 ■ a s

σ _в и σ _s — кгс/мм²

[19]

19

a s = a o ■ e m ■ E n ■ exp ( - pT ) ; т ф = 0,577 ■ a s

E — скорость деформации; Т —температура; a₀, m , n и p постоянные для данного материала величины.

Сталь 45 ( Т = 900—1300 °С): a₀ — 138, n — 0,25, m — 0,14 , p — 0,2510 ^{- 2} .

12Х18Н9Т ( Т = 900—1200 °С): a₀ — 340 ; n — 0,28 ;

m — 0,09; p — 0,2810 ^{- 2} .

Титан ( Т = 200—750 °С): a₀ — 190; n — 0,35;

m — 0,10; p — 0,310 ^{- 2} .

[22]

20

a и — 133 ■ E ⁰,²⁵² ■ E ^0/14 ■ e - ⁰-^{002 T} ;

ст     ^ЭГ Г- 0,28 Д.0,087 ^-0,0028 T

О — 325 ■ E ■ E ■ e        .

и

Сталь 45 ( Т = 800—1200 °С). 12×18Н9Т ( Т = 900—1200 °С)

[23]

21

т ф — т 0 TJ      J ■ exp ( - B ■ LT ' )

V ^E0 ) V ^E0 )

E₀ — предел текучести, деформация и скорость деформации для базовых условий; m , k и B — показатели деформационного и скоростного упрочнения и температурного разупрочнения материала;

LT' — T - T 0 — приращение гомологической темпера

туры

[8]

22

^т ф = S B ' A^k E ■ ^E P ' exP 1 ^B ■ ^LT ' )

A — { V3 [ ^/3 - ln ( 1 + E _z ) ] m }

А , k _ε и В — эмпирические константы, учитывающие влияние Т, E, E на предел текучести; LT' — приращение температуры

[8]

23

т — s, ■ A ■ k ■ e m Vi + A ■ A ¹ ■ k ^E ■ E ^{1 - p} )

^ф B      ^{E p} V      1 + m ^P J

Б. Касательные напряжения τ _пп на передней поверхности

24

т пп — 0,252 ■ a _B

[1]

25

^т пп ^{— 0} в V^{1 + б} ) ■ ^cos2 ( ф ^- У )

[2]

Предложенная в [2] формула (табл. 1, № п/п 25) даёт возможность установить не только истинный предел прочности на разрыв S _B = а _в ( 1 + 5 ) , но и влияние на т пп угла сдвига ф (косвенная характеристика процесса деформации при резании).

Как следует из табл. 1, касательные напряжения сдвига τ_φ определялись в основном экспериментальными данными и зависят от механических характеристик материала: твёрдости ( НВ ), предела прочности (σ _в ), относительного удлинения (δ), поперечного сужения (ψ) (табл. 1, № п/п 1—10,). Известны попытки связать величину τ_φ с твёрдостью стружки HV измеряемой за зоной вторичных деформаций (№ п/п 8) и учесть влияние температуры на напряжение сдвига (№ п/п 5).

Таблица 1

Зависимости для оценки напряжений в зоне резания

№ п/п	Расчётная формула	Обозначения	Источник
1	2	3	4
А. Касательные напряжения в плоскости сдвига
1	Т ф = 73 ■ S b = 73 ■ а в -(1 + 5)	временное сопротивление разрыву; δ — относительное удлинение; Sb = а в ( 1 + 5 ) — истинное временное сопротивление разрыву	[2]
2	тф = а s /73 = а s /1,73 = 0,577 ■ а s , условие пластичности Губера — Мизеса	σ s — напряжение течения	[17, 18]
3	тф = 0,7 ■ S B = 0,7 ■ а в ( 1 + 5 ) ; тф = ( 0,8 - 0,97а в
4	т ф = а в '( 1 + К т ■ 5 ) К т = 0,9 ( 5 >  0,06; ф = ( 1,2 - 1,5 ) - 5 ) К т = 1 S b = а в ( 1 + 5 )	Ψ — поперечное сужение	[2, 12]
5	т ф = S b .( 1 - 0,5.10 - 3 ■ T ) ( 200 <  Т деф <  600; 650 <  Тпп <  1200 )	Τ — температура, °C	[3]
6	т ф = 0,6 ■ а в -(1 - 1,7 ■ ф )
7	т ф = k ■ а в	к = 0,925 — углеродистые стали; к = 1,3 — нержавеющие стали; к = 0,6 — титановые сплавы	[4]
8	т ф = 0,185 Н/	твёрдость стружки по Виккерсу, измеряемая за зоной вторичных деформаций	[1, 4, 5, 10]
9	тф = 0,165 ■ C 2 ■ HB	коэффициент предельного упрочнения; HB твёрдость обрабатываемого материала	[2]
10	тф = Sb = а в 71 + 5 )
11	т ф = ( P NO ■ cosY + P ZO ■ sinY )/( b ■ l n )	γ — передний угол; PNO и PZO — нормальная и тангенциальная силы резания (без учёта сил на задней поверхности); b — ширина среза; lп — длина контакта по передней поверхности	[1]

Продолжение табл. 1

Окончание табл. 1

1	2	3	4
26	т пп = 0,28 • а в -( 1 + 5 )		[11, 12]
27	т пп = ( 0,5 - 0,6 ) . S b = ( 0,5 - 0,6 ) . а в -( 1 + 5 )		[3]
28	т пп = 0,6 • S B = 0,6 • а в '( 1 + 5 )	Для сталей ферритного класса	[8]
29	т пп = тф	Для углеродистых сталей	[8]
30	т пп = 0,5 • тф		[17]
В. Касательные напряжения τ зп на задней поверхности
31	т зп = 0,252 • а в		[1]
32	т зп = 0,5 • тф	τφ — напряжение сдвига	[11]
33	т зп = в • М • а s = 0,577 • а s = т ф	Для плоского деформационного состояния; β — коэффициент Лоде; μ — коэффициент трения, определяемый по напряжению текучести	[17]
34	т зп = ( 0,7 - 0,8 ) . SB = ( 0,7 - 0,8 ) . а в ( 1 + 5 )		[8]

Ряд авторов [1, 5, 8, 12, 13] определяют τ_φ , исходя из энергетического (теплового) баланса в зоне резания. Принимается следующая схема. Вся работа резания Q = P z -V полностью переходит в тепло, которое распределяется по трём каналам — зона деформации ( Q _д ), передняя ( Q_пп ) и задняя ( Q_зп ) поверхности инструмента:

Q = Q g + Q nn + Q зп . (1)

Теплота деформации — Q_g = т_ф • V_g • a • b[ sinф, где V_g — скорость сдвига. Следовательно, подставляя в формулу (1) это выражение и известные соотношения для Q_пп и Q_зп [1], находят напряжения τ_φ .

Для ориентировочных оценок усилий резания и температур на контактных площадках инструмента оправдано и не даёт существенных погрешностей определение напряжений по комплексу механических характеристик обрабатываемых материалов — а в , а₀ 2 , S _в = а _в ( 1 + 5 ) и HB .

Однако известно, что в условиях резания при наличии значительных деформаций, определяемых коэффициентом утолщения стружки k_a и относительным сдвигом ε, механические характеристики материала, превращаемого в сливную стружку, отличаются от стандартных [2, 3, 6, 8, 12, 13, 14].

Зависимости максимальных касательных напряжений τ и деформации сдвига ε при резании и при механических испытаниях сталей исследованы Т. Н. Лоладзе [6]. Установлено, что с увеличением £ растут и т. Так, для углеродистой стали 40 напряжение т_{£ - 1} = 780МПа, а для £ = 3 напряжён т уже равно 880 МПа (увеличивается на 13 %).

Н. Н. Зорев [12, с. 159] полагает, что зависимость между твёрдостью и напряжением при сжатии, растяжении и кручении в пластической области «едина для всех металлов» и выражается простой формулой т = 0,185 HV [12, с. 109]. Связь касательного напряжения сдвига т_ф относительным сдвигом при пластической деформации с достаточной точностью может быть выражена показательной функцией, предложенной Н. Н. Зоревым [12] (табл. 1, № п/п 16):

т_ф = A • £ m . (2)

Здесь А — константа, равная пределу текучести материала на сдвиг при относительном сдвиге, равном единице; m — константа, характеризующая способность материала к упрочнению при пластической деформации.

Специалисты в области обработки металлов давлением считают [17, 18], что τ_φ с напряжением течения σ _s (термин из [18]) связано условием пластичности Губера — Мизеса

Тф = о s/ V3 = 0,577 • о s(3)

а напряжение течения σ _s можно рассчитать на основе экспериментальных данных по формуле [19]:

о = т • еn = о • Еn(4)

SЕ

Здесь m = о_Е = 1 напряжение течения при е = 1 ; е — степень деформации (относительный сдвиг); n — показатель деформационного упрочнения, равный n = 0,173 для стали 45, n = 0,37 для 12х18Н9Т и n = 0,128 для сплава ОТ4.

В. А. Кроха [19] получил экспериментальные кривые упругости при сжатии и растяжении вида о _s = f ( е ) для широкой гаммы сталей и сплавов. Используя их и № п/п 15 табл. 1, зная о_Е = 1 , можно рассчитать значения σ _s . На рис. 1, заимствованном из [19], показана последовательность нахождения о _s . В случае отсутствия экспериментальных данных для зависимости о _s = f( е ) , можно использовать эмпирическую формулу (№ п/п 18 табл. 1).

0$, кгс/мм²

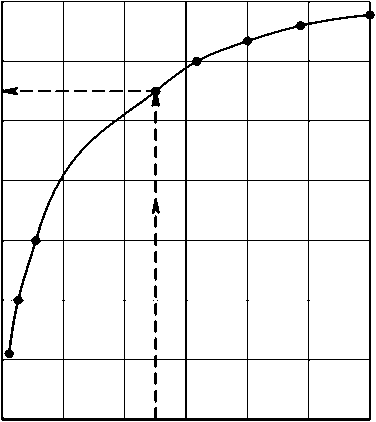
140 as= 130

Е = 1.00.4     0,8      1,2       1,6      1,8 Е

Рис. 1. Связь между напряжением текучести и степенью деформации при сжатии стали 12×18Н9Т (температура 20 °С) [19]

Резание металлов — термомеханический процесс, протекающий при высоких температурах и больших степенях и скоростях деформаций. Известно, что при увеличении скорости деформации напряжение текучести возрастает, а пластичность падает, что особенно проявляется для высоколегированных сталей. Менее чувствительны к изменению скорости деформации углеродистые конструкционные стали [18, с. 69].

При горячей пластической деформации надо учитывать влияние двух противоположных процессов — упрочняющего (возврат) и разупрочняющего (рекристаллизация), а также тепловой эффект пластической деформации. Тепловой эффект уменьшается с увеличением температуры деформации, так как с повышением температуры падает напряжение текучести и снижается энергия, необходимая для деформации. Поэтому при одной степени деформации образца в холодном и горячем состоянии в последнем случае теплоты выделяется меньше.

Напряжение текучести зависит от скорости деформации при заданной температуре и степени деформации. Известно, что в зависимости от отношения температуры деформации к температуре плавления (TT ™ ) увеличение скорости деформации е на два порядка вызывает рост напряжения текучести σ _s 1,16—3,4 раза [18]. Для углеродистой стали 45, жаропрочной стали 12×18Н9Т и титанового сплава ВТ3-1 найдено, что с увеличением скорости деформации на три порядка напряжения текучести возрастают в среднем в 1,4—1,7 раза [19].

Представляют практический интерес экспериментальные формулы для расчёта напряжения текучести при обработке давлением (учитывается совместное влияние деформации, скоростей деформации и температуры [22, 23] (№ п/п 19, 20 табл. 1). Их общий вид — это сочетание показательных и экспоненциальных функций:

a s = а₀ • е m • е n • exp ( -pT ) .                                       (5)

Параметры σ₀, m , n и p зависимости (5) выбираются на основе экспериментальных данных.

В [8, с. 175] приводится «обобщённое определяющее уравнение» (№ п/п 21 табл. 1) для расчёта τφ :

mk

I I I I

Т ф = T o I I • exp ( - B • A T ‘ ) .                                     (6)

l ^Eo ) I ^Eo )

Здесь A T = T - T 0 приращение гомологической температуры; T = 0 Т л ; T 0 = 273 T л ; 0 — температура деформации, (°С); е — деформация; е — скорость деформации; т₀ — предел текучести (МПа) для базовых условий; m , k , B показатели деформационного и скоростного упрочнения и температурного разупрочнения материала.

Зависимость (6), как отмечается в [8], используется при исследовании процесса горячей прокатки. Без учёта скорости деформации (при резании скорость деформации на 8—9 порядков выше, чем при статических испытаниях) зависимость (6), по мнению автора [8], примет вид (№ п/п 22 табл. 1):

Т ф = S_B • A • k , • е p • exp ( -B • A T ‘ ) ,                                     (7)

где A = { V3 ^V3 • In ( 1 + е _z ) ] } ; А , k, , B — эмпирические константы, учитывающие влияние скорости деформации и температуры на предел текучести.

В [8] отмечено, что уравнение (7) не может быть использовано для расчёта предела текучести при резании, так как в условиях резания приращение температуры A T' есть функция деформации ε _p предела текучести τ _р . Для адиабатических условий деформации в [8] предлагается зависимость (формула 23, таблица 1):

т =5 ■ А ■ к ■ е m -11 + A l A l l k c. е^1-р |

1 ф S B A ^k E ^е p l^{1 +} 1 + m ^ь p I .                                    ⁽⁸⁾

К сожалению, в [8, 15] не приводятся значения параметров A , A ₁, k _ε и S_B , поэтому воспользоваться зависимостями табл. 1 (№ п/п 22, 23) для оценки τ_φ при обработке резанием не представляется возможным.

Для расчёта температур на передней и задней поверхностях инструмента необходимо знать и касательные напряжения τ _пп и τ _зп [9].

В табл. 1 представлены известные из литературы данные для определения τ _пп (№ п/п 24) и τ _зп (№ п/п 31—34). Причём рекомендуется эти напряжения выбирать:

• —    по традиционной схеме, когда т пп = т з = 0,252 • о в [1];

• —    от доли истинного напряжения на разрыв S_B обрабатываемого материала (№ п/п 25—27, 33 табл. 1);

• —    в зависимости от напряжения в плоскости сдвига (№ п/п 28, 29, 32 табл. 1).

Из представленных данных по оценке напряжений в зоне резания следует предварительный вывод о том, что касательные напряжения τ _пп и τ _зп могут быть функционально связаны с напряжениями в плоскости сдвига τ_φ . Оценим влияние на τ_φ величин относительного сдвига (степени деформации) е , скорости деформации Е и температуры T .

Определение напряжений в плоскости сдвига τ_φ при резании. Отметим особенности деформации в условиях резания.

• — В основу большинства зависимостей для расчёта τ_φ (см. табл. 1) положены стандартные характеристики механических свойств материала, получаемые при растяжении стандартным методом, когда скорость деформации равна 1·10^-3с^-1. Если речь идёт об обработке давлением и резании даже на малых скоростях (около одного сантиметра в минуту), скорость деформации составляет 1—10 с^-1, что на 3—4 порядка больше скорости стандартных испытаний [6]. В результате не учитывается влияние скорости деформации при резании на характеристики механических свойств материалов (σ _в , S_B , σ_0,2 , δ и ψ ).

— В реальных скоростных условиях механической обработки и пластического деформирования степень и скорость деформации влияют на напряжения — и при обработке стали с ростом скорости деформации напряжение текучести увеличивается [6, 14, 18, 19, 24].

— Предварительное упрочнение пластичного материала различными способами повышает напряжение текучести, что необходимо учитывать при оценке τ_φ . В соответствии с № п/п 8 табл. 1 можно рассчитать т_ф = 0,185 Н^ первичной твёрдости стружки [12, 13, 14, 16], которую следует измерять за зоной вторичных деформаций [6].

С учётом этих замечаний из рассмотренных в табл. 1 зависимостей найдём подходящие для расчёта сдвиговых напряжений τφ . Учтём опыт специалистов в области обработки давлением по экспериментально-расчётной оценке напряжения течения (во внимание принимается температура, степень и скорость деформации).

Критерием применимости выбранных формул для τ_φ , а также для τ _пп и τ _зп будет, очевидно, сравнение расчётных и экспериментальных значений температур резания при точении.

Для оценок величин е и Е принимаем плоскую схему деформации с единственной плоскостью сдвига, используя зависимости, полученные основоположниками отечественной науки о резании материалов К. А. Зворыкиным, И. А. Тиме, и уточнённые Н. Н. Зоревым, Т. Н. Лоладзе, А. М. Розенбергом и А. Н. Ерёминым, М. И. Клушиным [16] и др.

— Относительный сдвиг (степень деформации):

Е = tg ( ф - Y ) + ctgф.                                      (9)

— Угол сдвига:

tgф =

cosγ k - sinY, a

где k_a коэффициент утолщения стружки, γ передний угол.

— Скорость стружки:

v = V c k a

— Скорость сдвига:

V = V . cos^Y сдв      cos ( ф - y )

— Скорость сдвига при резании [2, 5, 12, 13, 16]:

E = E = E .V lB” MV " Д X • k a

В зависимости (13) Δ х толщина сдвигаемого элемента, обычно определяемая по корням стружек.

По данным Т. Н. Лоладзе, Δ x находится в пределах 0,02 ÷ 0,005 см [6, с. 68]. При этом k_a = 2 ^ 4 и e = 2 ^ 5 А. М. Вульф [14, с. 84] просто принимает величину Д х , равную 0,02 мм. Ориентировочные расчёты величины Δ x для резания отсутствуют.

• У. Джонсон, П. Меллар [20] и А. Л. Воронцов [17, 24] для плоской схемы резания вводят понятие скорости разрыва V_p = V • sinф . При этом накопленная деформация e определяется за-

• висимостью [20]:

cosγ

E =-------------- 7 --------г.

sinф • cos ( ф - y )

Примечание. В графу 10 табл. 3 внесены данные расчётов τ_φ по формуле (14) Джонсона.

Определение толщины зоны деформации и скорости сдвига при образовании сливной стружки. Рассмотрим схему образования сливной стружки (рис. 2). Из предложенной схемы видно, что толщина Δ х связана с толщиной среза a .

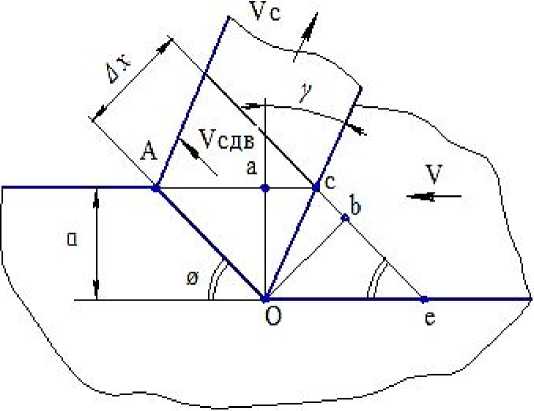
Рис. 2. Определение толщины деформированного слоя при резании

Д x = OB = OC • cos Z COB = AO- • cos Z COB = s lsln£

cosγ

cosγ

• cos [Z COE -Z BOE ] =

s c ^^Пф • cos [ ( 90 ° - v ) - ( 90 ° - Ф ) ] = s • sinф •

cos ( ф - Y )

;

cosγ

.     cos ( Ф - v )

Д x = s • sinф---------

.

cosγ

Определим Δ x для точения стали 12×18Н9Т резцом ВК8 при

V = 1,07 м/с; t = 0,5·10^-3 м;

s = 0,14·10

-

'³ м; k a = 1,53; Z v = 0 ° ; Z ф = 45 ° ; Z ф = 31,63 ° :

cos^Ф - v)            ,

0,851 1

= 0,08 • 10 ^{- 3} м

Дх = s • sinф--(     ) = 0,14 • 10-3 • 0,707 • cosγ

Подставив Δ x в (13), найдём скорость сдвига:

_E = j V, = V /g^(ф - _v ) + ^ctg^ф =

2,19

0,08 • 10 ^{- 3} • 1,53

= 0,19 • 10 5 c ^{- 1}.

Дx -к       Дxk aa

Ниже представлены обобщённые данные вычислений касательных напряжений в плоскости сдвига τφ , рассчитанных нами по формулам, приведённым в табл. 1. Для удобства анализа результа- ты оценок τφ по механическим характеристикам обрабатываемых материалов сведены в табл. 2. Здесь же в графе 7 представлены значения τφ . Они получены в результате замеров твёрдостей стружек. Для этого стали 45, 12×18Н9Т и сплав ВТ3-1 точили при V = 1,07 м/с с сечением среза t xs =(0,5x0,14) "10-6 м2. В графах 9, 10 и 11 табл. 2 даны значения тф, рассчитанные с использованием формул сил резания по данным [8, 25, 26].

Таблица 2

Напряжения сдвига τφ , МПа

№ п/п	Пара	Значения, рассчитанные по механическим характеристикам обрабатываемых материалов						Значения, рассчитанные по уравнению энергетического баланса ( t = 0,5 • 10 - 3 м, s = 0,14 . 10 - 3 м/об)			Средние значения τφ рассчитанные по формулам
		Источник (№ п/п табл. 1)
		1	4	10	7	8	3	13	14	15	19	20
1	2	3	4	5	6	7	8	9	10	11	12	13
1	СТ45/Т15К6 а в = 598 МПа ; б = 0,16; ф = 0,4; V = 0,99 м/с; P z = 186 Н ; P y = 0,84; Px = 65 Н	1202	684	694	553	592	478— 598	701	736	723	606	935
2	12×18Н9Т/ВК8 а в = 630 МПа; б = 0,35; Ф = 0,4 ; V = 1,07 м/с; P = 233 Н; P = 96 Н; P = 62 Н z               yх	1471	838	851	819	932	504— 630	890	1026	877	2722	2421
3	ВТ3-1/ВК8 а в = 930 МПа; б = 0,14; Ф = 0,45 ; V = 1,06 м/с; P = 176 Н; P = 79 Н; P = 62 Н z               yх	1845	1302	1060	558	895	744— 930	725	801	651	377	—

В табл. 3 в качестве примера приведены необходимые исходные данные для расчёта степени и скорости деформации при резании обрабатываемых материалов, отличающихся деформационными и прочностными показателями.

Таблица 3

Исходные данные и результаты расчёта τφ учётом влияния степени деформации

Пара	Данные авторов тф = 0,577 ■ о s							Результаты расчётов по формулам из [19]							Результаты расчётов по формуле из [20]
			9-\|		ш	Z о 2	о -W	о s = ОЕ = 1 ■ Е П				0 s = (1,83 ■ 0 в		+ 4)" Е n	ш	0 s = f ( Е )
									£ о	£ Z о	£ Z о LH О II 91-	+ о гз ^ со и" С!/ 9 1-	Z о	£ Z о LH О II 91-		£ Z о	£ Z о LH О II 91-
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
	0,63	1,61	30,14	0,39	2,42	0,06	0,15			1286	742		1283	740	2,37	1450	819
СТ45/Т15К6	0,99	2,29	22,72	0,43	2,91	0,07	0,18			1320	761,6		1318	760	2,92	1480	808
Z ф = 35 ° ,	1,57	3,13	17,24	0,50	3,64	0,074	0,25	0,173	1100	1370	740,5	1098	1367	789	3,52	1500	866
Z y = - 5 °	2,5	3,71	14,1	0,67	4,21	0,075	0,38			1223	705,7		1221	705	4,21	1600	923
	3,14	2,18	23,7	1,44	2,82	0,07	0,58			1262	728		1259	726	2,82	1400	808
	0,34	1,78	28,12	0,19	2,54	0,083	0,058			1692	976		1631	941	2,44	1480	810
12×18Н9Т/ ВК8	0,68	1,85	27,25	0,37	2,55	0,084	0,112			1693	976		1631	941	2,58	1450	837
Z ф = 45 ° ,	1,07	1,53	31,63	0,70	3,36	0,079	0,30	0,37	1300	1872	1080	1157	1805	1041	1,94	1300	750
Z y = - 5 °	1,36	1,05	41,34	1,30	2,15	0,068	0,41			1656	956		1597	921	2,20	1350	819
	2,14	1,55	31,41	1,38	2,35	0,079	0,41			1656	956		1597	921	2,38	1400	819

Экспериментально определяли лишь коэффициент утолщения стружки k_a . Параметры φ, скорости сдвига, движения стружки находили по классическим зависимостям (10)—(14). Толщина зоны деформации Δ x определилась по полученной нами упрощённой зависимости (15). Напряжение течения σ _s находили по методике В. А. Кроха по зависимостям (№ п/п 17, 18 табл. 1). Причём напряжения о_Е = 1 при относительном сдвиге е = 1 принимались из графиков для стали 45, 12×18Н9Т и ВТ3-1 работы [19]. Использование графиков вносит погрешности в оценку величины о_Е = ₁. Поэтому для определения т_ф целесообразно использовать № п/п 18 табл. 1:

т_ф = 0,577 - ( 1,83 ■ о в + 4 ) ■ е n .

Здесь о в в кгс/мм².о s = f ( Е )

Применяя классическую зависимость (9) и формулу (14) Джонсона и Меллара [20], мы не обнаружили практической разницы в оценках относительных сдвигов (данные граф 6 и 16 табл. 3 практически совпадают). Расчётные данные удовлетворительно согласуются и для τφ , особенно для титанового сплава ВТ3-1.

Мы попытались использовать для расчёта напряжений τ_φ экспериментальные зависимости с учётом влияния на σ _s степени и скорости деформации и температуры [22, 23] (№ п/п 19, 20 табл. 1). Оказалось, что формула М. Я. Бровмана [22], представленная в табл. 1 (№ п/п 19), даёт следующие средние значения τ_φ : — 511—671 МПа (сталь 45);

— 2197—2486 МПа (сталь 12×18Н9Т);

— 330—404 МПа (сплав ВТ3-1).

Расчёт по формулам А. В. Третьякова [23] (№ п/п 20 табл. 1) показал следующее. При резании величина τ_φ в зависимости от скорости резания колеблется в пределах 664—1029 (т_ф = 35 МПа) (для стали 45) и 1889—2468 МПа (для стали 12х18Н9Т). В графах 13 и 14 табл. 3 для сравнения приводятся рассчитанные по этим формулам значения τ_φ в выбранном диапазоне скоростей для каждого обрабатываемого материала. Их значения представляются нам сильно завышенными, кроме данных для стали 45.

Какие выводы можно сделать из сравнения данных таблиц 2 и 3? Какие соотношения следует рекомендовать для расчёта напряжений τφ в плоскости сдвига? Прежде всего, должно быть учтено влияние различных параметров процесса резания — например, таких, как:

— деформации (в частности, их скорость);

— температуры в зоне деформаций;

— механические характеристики обрабатываемых материалов;

— геометрия инструмента;

— элементы режима резания;

— характеристики инструментальных материалов.

Таким требованиям в наибольшей степени удовлетворяют:

• — формулы для расчёта τ_φ , полученные из уравнения энергетического баланса процесса резания (№ п/п 13—15 табл. 1);

— формула, учитывающая твёрдость стружки, измеренную за зоной вторичных деформаций.

Только в этих случаях косвенно учитываются все условия проявления температурнодеформационного фактора при резании.

При этом особенно предпочтительна зависимость, полученная нами из условия баланса зо- cosγ ны резания по уравнению (5), представленного в [5], с учётом Rnp= тт • a • b • V---—-—- • sinф деф ф          cos (ф - у )

(№ п/п 14 табл. 1).

Нахождение τφ измерением твёрдости стружки даёт стабильные результаты для резания с толстыми стружками (средними и большими подачами), поэтому данный метод может быть рекомендован как контрольный.

Расчёт τφ по формулам В. А. Крохи [19] (№ п/п 17, 18 табл. 1), учитывающим влияние и степень деформации, даёт результаты, совпадающие до 3—7 % с данными № п/п 14 табл. 1.

Из предложенных зависимостей для оценки τ_φ по механическим характеристикам обрабатываемых материалов в качестве первого приближения следует принять т_ф = S_B = о в -( 1 + 5 ) (№ п/п 10 табл. 1).

В итоговой табл. 4 приведём в качестве примеров рекомендуемые зависимости для расчёта τφ и напряжений τпп и τзп . Сталь 45 обрабатывается резцами Т15К6 на режимах t х s =(0,5 х 0,14)-10 6 м2 при различных скоростях.

Для температурных расчётов в дальнейшем принимаем следующие зависимости. Вариант 1 (предварительный расчёт температуры):

т ф = 0,577 • о s = 0,577 - ( 1,83 • о в + 4 ) • £ ⁿ ; т _лл = о в ■ ( 1 + 5 ) • cos2 ( ф - у ) ;

т зп = 0,5 ■ Т ф = 0,5 ■ 0,577 . ( 1,83 ■ о _в + 4 ) ■ е n .

Вариант 2 (предполагаемые максимальные уровни температур в зоне резания):

Pz • sinф - тф =----------

I P if 1

1 - sin y + — ■ cosY ■ v-

I       Pz       J I ka a ■ b

cos ( ф - Y )

: т = т = т

; пп     зп     φ cosγ пп    зп    φ

Возможны и промежуточные варианты выбора формул для расчёта τ_φ , τ _пп и τ _зп — когда τ _пп и τ _зп изменяются от минимальных до максимальных значений, например для пары СТ45/Т15К6 Т пп = Т зп = 151—780 МПа (табл. 4).

Таблица 4

Рекомендуемые зависимости для оценки напряжений τ_φ , τ _пп и τ _зп

Касательные напряжения в плоскости сдвига τφ , МПа	Рассчитаны по механическим характеристикам
	Т ф = 0 в '( 1 + 5 )	694
	Т ф = 0 в '(1 + К Т ■ 5	684
	Рассчитаны с учётом деформаций, скоростей деформаций и температур при различных скоростях, м/с
	Т ф = 0,577 ■ 0 е = 1 ■ е n	V = 0,63	V = 0,99	V = 1,57	V = 2,5	V = 3,14	τ φ ср
		705	726	740	760	780	746
	Т ф = 0,577 - ( 1,83о в + 4 ) е n	740	760	789	705	726	744
	Т ф = 0,577 ■ о0 ■ е m ■ е n ■ exp ( - pT ) , ( T = 800 °C)	511	555	620	670	671	606
	Рассчитаны по уравнениям энергетического баланса
	№ п/п 14 табл. 1	Т фср = 736
	№ п/п 15 табл. 1	Т фср = 770
τ пп , МПа	т пп = 0,252 ■ о в	151
	Т пп = 0,5 ■ 0 в -( 1 + 5 )	347
	Т пп = S в ■ cos2 ( ф - Y )	229	396	493	545	—	421
	Т пп = Тф	705	726	740	760	780	746
	Т пп = 0,5 ■ Тф	352	363	370	380	390
τ зп , МПа	Т зп = 0,252 ■ о в	151
	Т зп = 0,5 ■ Тф	352	363	370	380	390	372
	Т зп = Тф	705	726	740	760	780	746

Выводы.

• 1.    Анализ известных литературных данных по расчёту напряжений в плоскости сдвига показал, что используемые в настоящее время механические соотношения не учитывают термодеформационного состояния зоны резания, поэтому их следует принять в качестве грубого приближения.

• 2.    Косвенно учитывают комплекс термодинамических процессов при резании и поэтому могут применяться для расчёта тепловых процессов:

• —    аналитические зависимости для расчёта τ_φ , полученные на базе уравнения баланса энергии при резании;

• —    экспериментальные данные оценки τ_φ по твёрдости стружек.

• 3.    Предложенные специалистами по обработке металлов давлением зависимости, содержащие степень деформации (относительный сдвиг) ε, применимы для расчёта τ_φ лишь как первое приближение. Значения ε получаются расчётами на основе классических зависимостей теории резания.

• 4.    Формулы для расчёта т_ф типа т_ф = А • £ m • £ k • exp ( -B • ДТ ‘ ) предполагают наличие экспериментальных результатов оценки постоянных А и В и показателей степеней m и n , хотя сам расчёт степеней и скоростей деформаций при резании трудностей не вызывает.