К вопросу определения коэффициента трения в быстропротекающих процессах силового взаимодействия

Трение и износ скользящих элементов в быстропротекающих процессах силового взаимодействия представляет собой предельный случай внешнего трения твердых тел, происходящего, как правило, в условиях больших скоростей взаимодействия (нескольких сотен метров в секунду) и больших контактных давлений (при которых материал хотя бы одной из пары находится в состоянии близком к пределу текучести), сопровождающийся также интенсивным тепловыделением, способным разогревать поверхность контакта T п до высоких температур, достигающих в предельных условиях температуры плавления T пл одной из трущихся пар.

Нагревание поверхностного слоя материала вблизи поверхности контакта приводит к изменению его механических свойств (рис.1) , которые определяют касательные напряжения сдвига тк и силу трения где S - площадь поверхности контакта.

При плавлении материала одной из трущихся пар фрикционное поведение пар трения определяется характером процесса плавления, свойствами и толщиной расплавленной пленки. Основными факторами, определяющими характеристики процесса высокоскоростного трения, являются его скоротечность и нестационарность теплофизических и механических процессов, определяемых режимами скольжения (с большим ускорением (разгон); с постоянной скоростью; с небольшими ускорениями замедления; с фрикционным торможением), оказывающими существенное влияние на характеристики процесса трения. Соблюдение перечисленных условий приводит к необходимости моделирования процесса на динамических установках с конструктивными параметрами, близкими к натурным образцам.

-^

F тр

J Т к dS, S

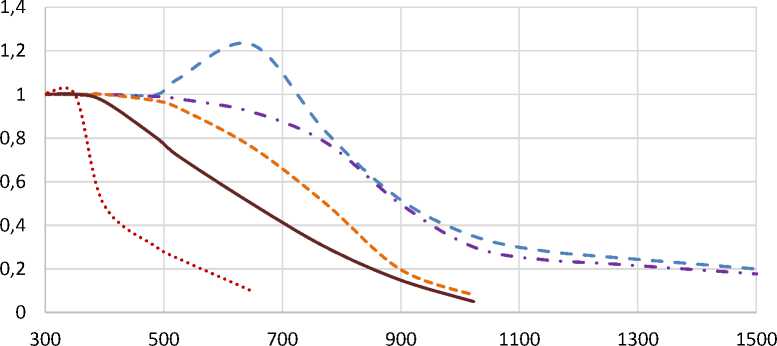
сталь3

Аллюминий

Сталь легированная, медь Польамид

Полипропилен

Рисунок 1 – Зависимость коэффициента разупрочнения материалов от температуры¹

Теоретические исследования процесса нагревания поверхности скользящего элемента тепловым потоком q 1 , выделяющимся при трении основываются на решении дифференциального уравнения теплопроводности для одномерного теплового потока в изнашиваемый скользящий элемент.

Наиболее подробные исследования теплового состояния контртел в условиях высокоскоростного скольжения приведены в работах Балакина В.А, в частности в [1]. Основываясь на изложенных в [1] подходах автором разработана и исследована, в том числе для практического применения в работах [2 – 5] интегральная математическая модель трения. В основу интегрального метода положено уравнение теплового баланса теплоты Q1, подводимой от сил трения, и аккумулированной в стенке QТ скользящего элемента

Qi = QT(3)

где

Q i = Jo q i ■ ^dt;    Q t = c_vp_v

Jo T dr,(4)

а также аппроксимации профиля температуры по толщине скользящего элемента r полиномом второго порядка (рис. 2)

T^A+B-г + Ог2.(5)

^“i^/^(2)

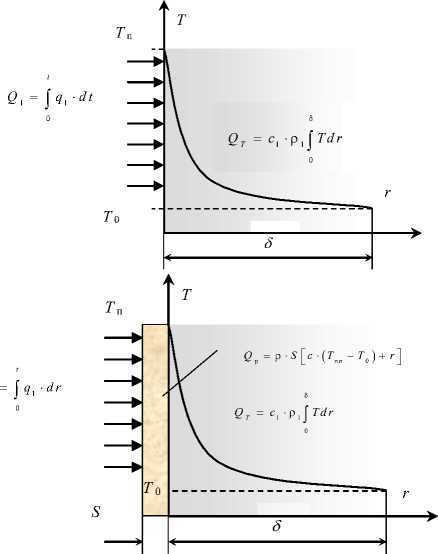
Рисунок 2 – Схема нагревания поверхности: а) – до плавления; б) – с плавлением

Поскольку глубина прогретого слоя 8 контактных элементов за время выстрела составит незначительную величину, то с учетом известного теплового потока q 1 на поверхности контакта, определяемого условиями силового взаимодействия скользящих поверхностей, краевые условия решения уравнения (2) записываются, как в случае полуограниченного тела:

-при г = да ^^dT(”, ^t)/^^ =

0,  Т( « ,t) = T o ;

-при г = 0 ^ Т(0,0) = То,  Т(0, t) =

Т п ;   (6)

1 ЭТп/ Q1 = --1   / дг, где T – температура в скользящем элемента;

• r, t – координата и время соответственно;

• a 1 , -₁ — коэффициенты температуропроводности и теплопроводности материала скользящего элемента;

• c 1 и ρ – теплоемкость и плотность ма-

5 = V6 • а • t.                 (8)

териала скользящего элемента.

Неизвестные коэффициенты А, В, С определяются из уравнения теплового баланса (3) и граничных условий (6):

сталь            медь алюминий      хром полиамид

Л = Т п ;

Q 1 ^^

^B=-^qt ^^-^-^

Т-

Т о = (Т п

Q i • 5

2 •-

— ТО-О-^ ■ (1-5)2

^Qt = ¹ • C i • P i • ⁵ • ^(Т п

-

Т о );

5 =

3 JpQ i dt

^C 1 • P 1 • ^(Т п

— Т о )"

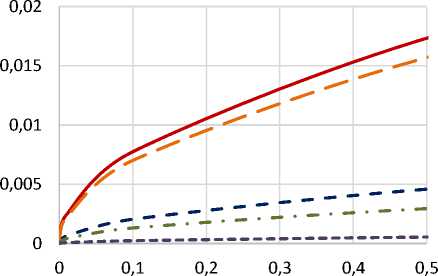
Для постоянного по времени теплового потока ( q 1 =const) получим формулу для глубины прогретого слоя δ времени t (рис.3)

Рисунок 3 – Зависимость глубины прогрева (м) от времени (с)

С учетом (8) температуру в скользящем элементе определим следующим выражением:

Т^о+О-^^-Г)2,(9)

2 • -1о тогда для температуры поверхности трения ( r =0) получим

Qi • 5

Тп   то-   ;   .(10)

^- 1

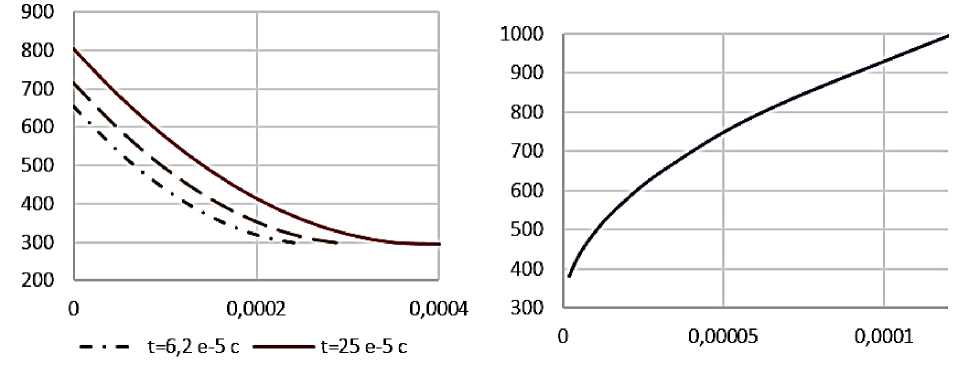
--t=12,5e-5c                                         ----LK а)                                         б)

Рисунок 3 – Изменение температуры при нагреве поверхности медного элемента при тепловом потоке q =2000 МВт : а) распределение температуры (К) по глубине; б) – изменение температуры поверхности от времени, с

Распределение температуры по глубине скользящего медного элемента приведено на рис.3. В таблице 1 приведены расчетные значения глубин прогрева различных материалов от времени подвода теплоты. Из табл. 1. следует,

что поверхностные слои металлических пар прогреваются на глубину 5, на порядок большую, чем пластиковые. За одно и то же время нагрева самый теплопроводный, в соответствии с табл. 2, металл – медь прогревается на глу-

бину, в 4 раза большую, по сравнению с глуби- чем полипропилен и в 55 раз большую, чем поной прогрева одного из наименее теплопровод- лиамид.

ных металлов висмута и в 24,4 раза большую,

Таблица 2.2 – Глубина прогрева

Материал образцов	а 104, м2/с	Глубина слоя 6, мм при t, c
		10-5	10-4	10-3	10-2	10-1	1	10
Армко-железо	0,08	0,018	0,057	0,18	0,57	1,8	5,7	18
Сталь 45	0,07	0,017	0,053	0,17	0,53	1,7	5,3	17
Медь	1,0	0,061	0,19	0,61	1,9	6,1	19,	62
Алюминий	0,82	0,056	0,175	0,56	1,75	5,6	17,	56
Висмут	0,06	0,015	0,048	0,15	0,48	1,5	4,8	15
Цинк	0,3	0,034	0,106	0,34	1,06	3,4	11,	34
Молибден	0,46	0,04	0,130	0,41	1,30	4,1	13,	41
Вольфрам	0,47	0,042	0,134	0,42	1,34	4,2	13,	42
Полипропилен	0,002	0,002	0,004	0,02	0,04	0,2	0,4	2,
Полиамид	0,001	0,001	0,003	0,01	0,03	0,1	0,3	1,

В случае оплавления поверхности скользящего элемента (рис.2 б) необходимо решение задачи Стефана. При этом в уравнении баланса (4) с учетом (5) тепловом потоке q 1 при возможном оплавлении контактной поверхности скользящего элемента, определится следующим:

q ₁

-

ат /        ■

λ ^{∂ T} + r ρ s , 1         _{∂ r}         1 1

где r 1 - удельная теплота плавления материала.

Граничными условиями решения уравнения (2) с учетом (10) и при допущении о по-лубесконечном теле будут:

-при t < tпл ^ s(t) = 0, s'(t) = 0, где: TПЛ - температура плавления материала скользящего элемента; s и s' -толщина расплавленного слоя и скорость плавления соответственно.

Время достижения температурой поверхности элемента температуры плавления материала получим из выражения (10):

2⋅λ ² ⋅ T - T

1         пл       0

t =                                  .

3 ⋅ q 1²

-при г = го ^

-при г = 0  ^

0, t >

9Т( го ,t)_/   _

/ 5г

Т( го ,t) = Т о ;

: tп_Л ^Т(O,t) = Т _Пл ;

По аналогии с (7), для момента времени t=t пл получим при r= 0 ^ T=T пл ; при r = 8 пл ^ T = T 0 , где δ - толщина прогретого слоя в момент времени t=t ПЛ

Т —

Т о = (Т пл

— То)^

—

-  ■' '     ^{41  8}   2..V--    ^ о ⁾²1

^Qt = з • С 1 • P i • ⁸ • ^(Т пл

—

Т о );

Для осредненного ( q 1 =const)

по времени

3 8 пл =  *

t потока

/o4 i ^8t/

' ^ 1 • Р 1 • (Т пл

—

Т о )

6 ⋅ a ⋅ t

1    пл

.

Окончательно для температуры в скользящем элементе запишем

Умножая правую и левую части уравнения (2) на dr и проинтегрировав его в пределах от r=s до r= δ , получим уравнение, называемое интегралом теплового баланса:

гр _ гр , 41 "  ⁸ пл

Т = То+^“яГ

•(1—^). (16)

О пл

Г 5 9Т

Л at

dr = «O — V 9г )₅

9Т

^U/ (18)

пл

В моменты времени t>t

положение

некоторой точки на температурной кривой относительно фронта плавления определяется координатой r - s , а толщина прогретого слоя соответствует значению δ - s . Получим

q1" (8 — s)/

Т = То+   7  .•(1

2 • Zi\

—

г \2 (8—^) • (17)

Заметим, что для всех значений r ≥δ , T=T 0 , следовательно и (^ЭТ/_Эг)₅ =0. В соответствии с (11) и с учетом а₁ = ^Vc_1P1 имеем

5Т\

^Л 1 ^ W) = — i + r i • P i • s = 0.     (19)

С учетом (19) перепишем

Г 5ЭТ

4 1 - ^C 1 • Р 1 J -7^+r + r₁-p,_L = = 0.    (20)

Проведя преобразования последнего выражения путем подстановки (17), вычисления производной ^Т/у^ и взятия инте-грала^ ^Т/^dr , получим формулу для вы- числения скорости плавления поверхности тре- ния в окончательном виде:

f_tnn 4 1 ⁽t)^dt ^— Vg • ^C 1 • Р 1 • ^(Т пл ^{— Т} о ) • V6 • a • (Vt ^— V^t ПЛ )

s(0 =

Проблемой решения тепловой задачи, основанной на уравнении теплового баланса (3)

является определение теплового потока qx (t), выделяемого при трении и направленного в скользящий элемент. Тепловой поток, направленный в сторону скользящего элемента и определяемый работой сил трения, при условии кулоновского трения можно вычислить при известном коэффициенте трения f и коэффици енте распределения тепловых потоков α q = α тп ⋅ fтр ⋅ v ⋅ p ,            (23)

где p - контактное давление;

v - скорость скольжения.

Значение коэффициента кулоновского трения для высокоскоростных условий как функцию скорости определяли многие исследователи. Многие из результатов приведены в работах [6 – 8]. Наиболее результативным методом экспериментальных исследований является метод с использованием газодинамических установок [8]. Основным результатом исследований явилось установление зависимости для коэффициента трения f вида

1 — а • v

= ^1+^'     (24)

учитывающей интенсивное падение его от начального значения f 0 в зависимости от скорости скольжения v , где коэффициенты а₁ и а₂ могут учитывать определенные условия процесса (разгон, торможение, материал и др.). Обычно большинством этих условий пренебрегают, не придавая большой значимости точности учета процесса трения. Так в работах [1, 4, 9] приводятся значения коэффициентов α 1 и α 2 0,003 и 0,072 для стальной пары и 0,0009; 0,0098 для пары медь-сталь соответственно.

В исследованиях [1 – 9], где поводится учет и анализ распределения тепловых потоков, при определении а _тп условия протекания процесса высокоскоростного трения характеризуют с помощью специальных обобщенных

4 1 ^—1 • ^С 1 • Р 1 • ^(Т пл ^{— Т} оУ ⁵

^ = Т^----------i---■  (21)

^[r 1 + - • С 1 • ^(Т пл ^{— Т} о ^)] • Р 1

где δ - скорость прогрева материала скользящего элемента, с учетом (7)

..J '      -

Интегрируя выражение (21) по времени получим глубину проплавления

^[r 1 + ² • C 1 • ^(Т пл ^{— Т} о ^)] • Р 1

критериев. К ним относят: число Пекле Pe, число Фурье Fo и коэффициент взаимного пе- рекрытия Kвз:

Pe = ^v^4a; Po = ^a^^t/_g 2 ;

К вз = ⁵¹/^₂.                (25)

Здесь v – скорость скольжения;

a – коэффициент температуропроводности;

l i – длина единичного пятна касания (в случае насыщения фрикционного контакта, связанного с увеличением нагрузки или разогревом трущихся поверхностей l i равно по величине длине площадки касания H ); t – время взаимодействия;

а2 - толщина рассматриваемого элемента пары трения;

S 1 , S 2 —номинальные площади касания первого и второго трущихся тел.

Так при малых скоростях интенсивность тепло q 1 и q 2 определяют пропорциональными коэффициентам теплопроводности материалов λ и λ контртел (предложено Х. Блоком [6]).

_ Я1   .     _        .

^а тп         ।      ; 4 1    ^а тп • ⁴ ;

4 2 = ^{(1 —} « тп ) • 4.           ⁽²⁶⁾

Для больших скоростей скольжения известны зависимости, учитывающие скоростной режим взаимодействия [1]:

-формула Д. Егера, полученная для стационарного источника теплоты и постоянной скорости скольжения ( v =const)

1,75 • Л1

“ ^тп     A _QC 1    , з _D 0,5    ^;

1,25 • Л 1 + Л 2 • Pe₂

-формула И.В. Крагельского, рекомендованная для расчета при больших скоростях скольжения (при числах Пекле Pe>20)

4^Л1

атп                        /----------■

4 • Л 1 +Л 2 • v^^pe ^

Подставляя значение а тп в формулу (23) получим замкнутую систему уравнений, решение которой позволяет в итерационном цикле определить коэффициент трения и температуру поверхности скользящего элемента в зависимости от скорости скольжения.

Введем в рассмотрение коэффициент, учитывающий динамичность процесса трения за счет изменения характеристики пластичности материала скользящего элемента к _т = °s(T)

/ _(т x (рис.1), тогда изменение коэффи-/ ° s v^j 0 )

циента трения от его начального значения определится формулой

/ Тр =/ о •к т .

В случае, если температура поверхности скользящего элемента достигнет температуры плавления T ПЛ , трение будет иметь гидродинамическую природу и коэффициент трения будет определяться в соответствии с законом Ньютона

/тр   Ир • V/p • 5р, где   бр- толщина расплавленной пленки;

р.р - коэффициент динамической вязкости расплавленного материала при температуре, близкой к температуре плавления.

При допущении, что расплавленная часть сразу же переносится на контртело (плавление с абляцией), а фронт плавления движется вглубь скользящего элемента со скоростью 5, текущее значение толщины расплавленной пленки 5 р определим следующим:

5 p =S^h/ _Vc ,

где h - ширина площадки касания в направлении скольжения.

Текущее значение интенсивности изна шивания /и:

/и = ⁵/v c ,

Если принять во внимание тот факт, что интенсивность абразивного изнашивания связана с разрушением материала, т.е. пропорциональна характеристикам, определяющим его прочность, то можно допустить, что и интенсивность изнашивания также будет возрастать от начального значения I_to обратно пропорционально коэффициенту разупрочнения:

I- = W

*1      /кт

Определение изменения коэффициента трения и интенсивности изнашивания при моделировании процесса является ключевым, поскольку его значение будет определять силовое и тепловое воздействие на ворс щеток и определять его изнашивание.

Для прогнозирования изнашивания абразивных пар при контактном взаимодействии принято [7] рассчитывать характерные удельные величины износа. К которым относят: Ih = dl/ds — интенсивность линейного изнашивания; /v = dV/^s — интенсивность объемного изнашивания; IG = dG/^s — интенсивность массо- вого изнашивания; Iw = dV/^

–

интенсив-

ность энергетического изнашивания.

Здесь: l,V,G - линейный, объемный, массовый износ, соответственно; 5 - путь трения; А - работа сил трения, которая может быть выражена зависимостью:

л г т-1 Г £          т

А = /тр • F J0 vcP dt,

где F - площадь контакта.

Для примера – у современных машин интенсивность линейного изнашивания трущихся пар I ^ , обеспечивающая их требуемый ресурс, составляет величину 10^-6 ÷ 10^-12 м/с.

Очевидно, что или другая характеристика абразивного изнашивания должна применяться в зависимости от условий, определяемых адекватностью эксперимента натурным условиям работы контактной пары.

При анализе процессов контактного взаимодействия твердых тел при высокоскоростном трении в большинстве случаев контртело можно принимать абсолютно жестким (так как 5 1 «5 2 ), а нагретые поверхностные слои скользящего элемента деформируемыми.

При этом будут учтены физические условия взаимодействия, определяемые теплофизическими характеристиками материалов пары трения и временем взаимодействия.

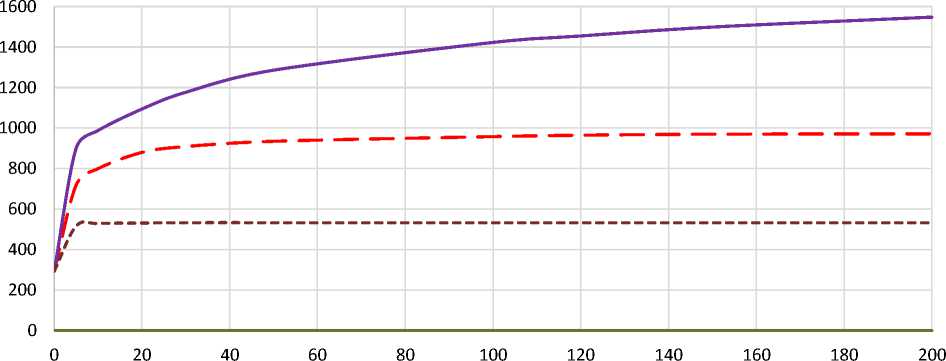
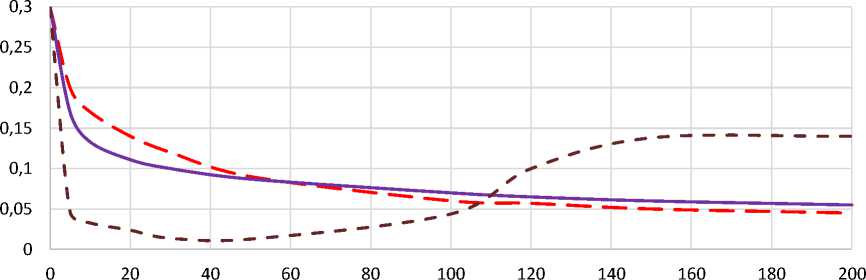
На рис. 4,5 приведены графики изменения температуры скользящих по стальной поверхности элементов, имеющих различные теплофизические свойства, и графики изменения их коэффициентов трения при различных скоростях скольжения, соответственно. Расчетные зависимости построены для элементов, шириной 50 мм при скольжении на пути 0,3 м.

Различный характер полученных кривых определяется существенным различием их теплофизических свойств. Так коэффициент трения стального элемента снижается более интенсивно, по сравнению с медным, от скорости на участке 0 – 50 м/с, затем его значение падает менее интенсивно. Полиамидный элемент расплавляется при скорости примерно 30 м/с, а затем его значение растет с ростом сил вязкого трения.

медь        сталь        Полиамид

Рисунок 4 – Изменение температуры от скорости скольжения

медь        сталь        полиамид

Рисунок 5 – Изменение коэффициента трения от скорости скольжения

Многие фундаментальные аспекты фрикционного взаимодействия остаются все еще не выясненными. Здесь в первую очередь следует сказать о формировании поверхностных контактных слоев. Известно, что тонкие поверхностные слои имеют иные физические свойства, чем материал объема. Это относится и к механическим свойствам. Не менее сложные задачи возникают и при изучении разрушения поверхностных слоев. Разрушение при фрикционном взаимодействии начинается сразу в большом количестве микрообъемов. Кроме того, область контакта практически недоступна для исследований в процессе фрикционного взаимодействия. Поэтому вопросы образования приповерхностных трещин, их объединения и эволюции во времени очень сложны для изучения. Большое влияние на фрикционное взаимодействие оказывает трансформация энергии трения, которая имеет место в контактном зазоре. Часть энергии идет на деструктивные процессы, а часть на прямой нагрев материала, что вызывает изменение механических свойств материалов поверхностных слоев элементов фрикционной пары и что, в дальнейшем, также сказывается на динамике процесса трения.

Построенная в данном исследовании математическая модель процесса трения получена на основании допущений, что теплообразование происходит на границе контакта рассматриваемых тел, источники теплоты которых являются плоскими. В действительности в нестационарных процессах в первые мгновения контакт может быть упругим. Затем с повышением температуры в зоне контакта и уменьшением механических свойств поверхностных слоев скользящего элемента контакт перейдет в пластическое состояние, характерное для насыщенного контакта. Если контакт ненасыщенный, то передача тепла происходит по некоторым площадкам, площадью Sj величина которых зависит от шероховатости поверхностей. Если контактная жесткость скользящего элемента ниже, чем у контртела, то происходит внедрение микронеровностей контртела в скользящий элемент. При этом максимум температуры наблюдается в слое, расположенном на некоторой глубине от поверхности трения. Здесь силы адгезии на границе контакта могут превысить прочность основного материала в этом слое и нагретые частицы будут переноситься на контртело. В процессе ненасыщенного контакта из-за уменьшения фактической площади контакта S = £ s. относительно общей 50, теплопередача к контртелу уменьшается, что приводит к росту аТП , а процессе мас-сопереноса нагретых частиц снижает его значение. Для учета этих процессов введем поправочные функции вд и в2, так что с учетом перечисленных факторов уточненное значение «ТП- а *  = а * -р , -р 2 ,                  (35)

тп       тп     α1    α2

где      р а1 = s/s 0 ; в „2 = ( I - q / ) ; q * - интен-

V              q 1 )

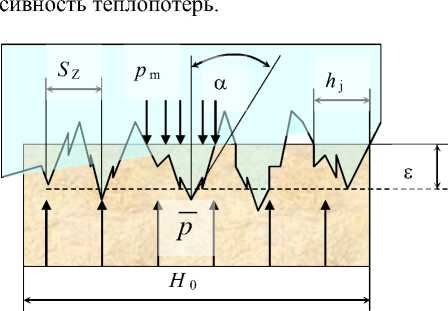
Рисунок 6 – Схема учета шероховатости контакта

Рассмотрим плоскую схему силового взаимодействия жесткой шероховатой поверхности контртела со скользящим элементом, представленную на рис. 6. При нормальном взаимодействии рассматриваемых поверхностей со средними контактными напряжениями p происходит внедрение вершин микронеровностей в скользящий элемент на глубину е . В направлении движения этих условиях теплопередача происходит по отдельным площадкам контакта h j , в сумме составляющих н = ^ н. . Тогда значение коэффициента определим формулой р_а| = £ hj/н_а . Задача силового взаимодействия по контактным площадкам может быть отнесена к контактным задачам о внедрении жесткого клина в деформируемое жесткопластическое полупространство для которой известно решение для удельной нормальной нагрузки по отношению к поверхности контакта

Р т = ° s ( ¹ + v ) ,          ⁽³⁶⁾

где v - угол пересечения линий скольжения у поверхности клина, связанный с углом полураствора клина формулой cos V cos (2 а - v ) = ---------.           (37)

1 + sin v

Поскольку известно, что в широких пределах изменения угла а величина v близка к п/2, при- мем его равным этому значению, тогда p = 2,5 -° ; Н°/ = Р/ = 0,4 - Рт/ .   (38)

m         s    /Н     p            ° ms

Обычно известны путем непосредственных измерений следующие параметры шероховатости поверхности RZ и SZ – высота и шаг микронеровностей, через значения которых можно определить размеры площадок касания и глубина внедрения по формулам:

h j = е- tg а ; Н ₀ = ^н/  -е- tg а;

z

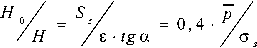
е = 0,8 - R

z

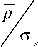
Пусть изнашивание поверхности скользящего элемента подчиняется абразивному за- кону, тогда интенсивность износа поверхности Jи вычислим по формуле

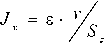
Подставив значения из (39), получим

J = 0,8 - v - и

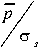
R

z

S

z

= k - v - п

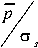
где k – коэффициент учета шероховатости , величина которого определяет форму поверхности. Для неизношенных поверхностей величину k можно принять в соответствии с таблицей 3.5, построенной по данным измерения соотношений высотных значений и базовой длины шероховатостей.

Таблица 2 – Значение коэффициента учета состояния поверхности

R Z , мкм	до 1,0	Св.1,0 до 12,0	Св.12,5 до 50	Св. 50 до 400
k п	0,004	0,012	0,020	0,050

Для изношенных поверхностей, подвер-женых трещиноватости вследствие температурно-фазовых превращений значения коэффициента k следует ориентировочно принимать наибольшим, приведенным в таблице 2, k =0,05. п ,

Величину теплопотерь вследствие абразивного износа q * определим через интенсивность изнашивания q. = c ■p ■ J = 0,8 ■ k ■ c ■p ■ p/  ■ T ,    (42)

1      11    и      ’      п    1    1    / <5     ср

s

где T – средняя температура уносимого в ре-

зультате износа материала

E

T

ср

= -■ f T ■ dr = T _o +

^E 0

q. ■ S (       1

1        1 +■

2 ■X Д   3

1   E )

■

2  S J

С учетом изнашивания поверхности трения формула (23) для расчета интенсивности теплового потока, направленного в скользящий

элемент примет вид

c. ■ p . ■ T ■ k q 1 = a тп-Р ■ v|/тр - 0,8 ■  1 P1 ср п I .   (44)

I                    ⁵ .       J

Анализ формулы (44) показывает, что для условий трения, приведенных в рассмотренном примере и при значении коэффициента учета шероховатости поверхности k =0,02 ин-

тенсивность теплопотерь q ^* достигает 20%.

Заключение

Изучение вопросов контактного взаимодействия твердых тел при высоких скоростях скольжения показывает, что повышение износостойкости трущихся пар тесно связано с необходимостью анализа процессов тепловыделения, распределения теплоты в области контактных температур и температурных полей, механических и адгезионных свойств нагретых поверхностных слоев, процессов, связанных с оплавлением поверхностей трения.

Таким образом, можно констатировать следующие особенности, которые необходимо учитывать при построении общей имитационной модели высокоскоростного трения:

• 1.    Высокоскоростное трение происходит в условиях тепловыделения в зоне фрикционного контакта и приводит к нагреванию контртел, изменению механических свойств их материалов.

• 2.    Изменение характеристик силового взаимодействия и интенсивности изнашивания в процессе трения в основном определяются напряжениями сдвига материала одной из пар вблизи контакта, которые в свою очередь зависят от его механических свойств. Исключением может быть некоторый инкубационный период, связанный с разрушением поверхностного слоя, имеющего особенности

• 3.    Механические свойства твердых тел являются зависимыми от многих факторов, основным из которых, при трении в указанных условиях, является температура.

• 4.    Трение при большом тепловыделении может происходить при плавлении материала одной из трущихся пар вблизи ее поверхности. В этих условиях фрикционное поведение пар трения определяется характером процесса плавления, свойствами и толщиной расплавленной пленки.

• 5.    Начальные значения коэффициента трения и интенсивности изнашивания (в заранее известных условиях, например, при установленной скорости скольжения и температуре контакта) являются зависимыми от многих факторов, определяющих взаимодействие контактной пары. Они могут быть определены экспериментально.

строения, вызывающие значительные отличия физических характеристик от основного материала.