К вопросу определения величины буксования при развороте гусеничной машины вокруг центра тяжести

Введение. Буксование в прямолинейном движении оценивается как разность теоретической скорости движения центра масс гусеничной машины и реальной скорости центра масс. При этом, естественно, оба борта ведут себя одинаково, буксование обеих гусениц совпадает. При развороте на месте центр масс не имеет линейной скорости, он только вращается вокруг одной точки, он и есть эта точка. Все остальные точки на корпусе и в теле гусеничной машины имеют линейную скорость, равную произведению угловой скорости корпуса относительно ЦТ на расстояние этой точки до ЦТ. Гусеницы вращаются в разные стороны с равной скоростью. Силы тяги на гусеницах направлены противоположно друг другу. Буксование каждой гусеницы – это разность между теоретической линейной скоростью точки корпуса, лежащей над геометрическим центром гусеничного обвода (серединой гусеницы по длине опорной поверхности, и серединой по ширине гусеницы).

Основная часть. При повороте гусеничной машины трак, лежащий на грунте, перемещается относительно земли (опоры) не только в продольном, но также и в поперечном направлении. Преодолевает сопротивление деформации грунта в продольном, поперечном направлениях и от вращения (подворота относительно центра трака). Это соответствует представлению Н.Е. Жуковского и его последователей в области теории движения гусеничных машин о силах и моменте трения плоского тела о грунт [1, 2].

Важно, что активной силой, преодолевающей этот конгломерат противостоящих сопротивлений, является все та же сила тяги на гусенице. Сила тяги, в свою очередь, обеспечивается только продольной (вдоль средней линии гусениц) составляющей деформации грунта – то, что принято называть буксованием. Назвать буксованием поперечную составляющую деформации грунта, или деформацию от вращения трака на грунте, нельзя – скорее это юз.

Так или иначе, в процессе поворота, а особенно ярко это видно при развороте на месте, только продольное буксование обеспечивает преодоление всех сил и моментов сопротивления повороту. Надо отметить, что далеко не все механизмы поворота позволяют разворачиваться на месте. Только появление бесступенчатых бортовых трансмиссий и дифференциальных механизмов поворота позволили получить это важное потребительское свойство в арсенал преимуществ гу-

сеничных промышленных тракторов.

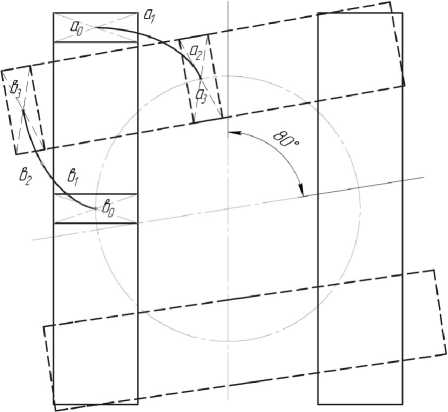
На рис. 1 приведена схема расположения траков, лежащих на грунте при развороте ГМ вокруг ЦТ, относительно траектории движения середины гусеничной тележки. Схема призвана показать величину преодолеваемых каждым траком расстояний и подворотов. Например, для трактора с дифференциальным механизмом поворота, изготовленного ОАО «Ходовые системы» совместно с ЮУрГУ в рамках комплексного проекта по созданию высокотехнологичного производства «Разработка бесступенчатого дифференциального механизма поворота со следящей системой управления для внедорожных дорожно-строительных машин нового поколения», радиус траектории R = B/2 = 0,94 м, а продольная база L = 2,86 м. Каждый трак сначала боком с подво-ротом перемещается примерно на 1 м (дуга a 0 - a 1 - a 2 - a 3 ), прежде чем попасть на траекторию центра гусеничной тележки, а потом совершает такой же путь в обратную сторону (дуга b 0 - b 1 - b 2 - b 3 ). Всё это графически показывает, насколько большие сопротивления нужно преодолевать дополни-

Рис. 1. Схема расположения траков,        тельным буксованием траков по касательной к лежащих на грунте при развороте ГМ вокруг ЦТ траектории центра гусеничной тележки.

С другой стороны, из теории движения гусеничных машин [3, 4] известно, что сила тяги зависит от радиуса поворота. Причем максимум сил достигается при радиусе, равном нулю, то есть при вращении вокруг центра тяжести. В свою очередь допустимый радиус криволинейного движения связан со скоростью балансом мощности. На рис. 2 приведены графики относительных сил тяг по бортам в зависимости от линейной скорости движения центра тяжести быстроходной гусеничной машины.

Из теории движения гусеничных машин также известно, что сила тяги пропорциональна буксованию по графику на рис. 3 [5, 6], причем прямо пропорциональна, в пределах упругой деформации грунта.

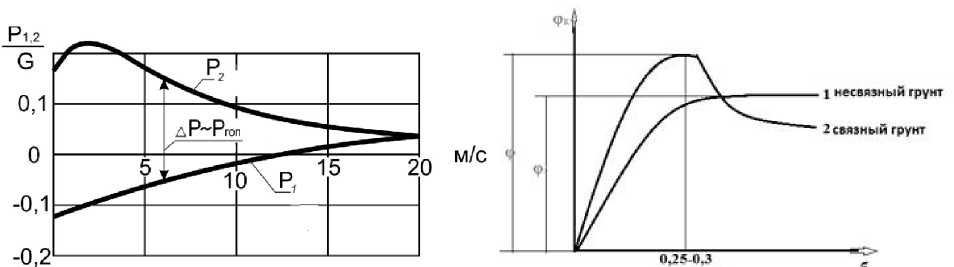
Рис. 2 Силы тяги по бортам в зависимости Рис. 3. Зависимость удельной (отнесенной к весу от скорости движения в повороте               машины) силы тяги от буксования

То есть в повороте, и особенно на месте, буксование траков должно быть значительно больше, чем при прямолинейном движении машины.

Величина буксования гусениц при развороте машины на месте определена с использованием формул из учебников по теории движения гусеничных машин [2–9]:

• 1.    При равномерном прямолинейном движении сила сопротивления равна силе тяги по формуле

• 2.    При неравномерном прямолинейном движенииР _ТЯГИ > Р соПР , а точнее

^Р ТЯГИ = ^ СОПР или ^—f СЦ = ^—f СОПР ,                                                (1)

где Р_ТЯГИ – сила тяги; P _СОПР – сила сопротивления; G – вес гусеничной машины; f _СЦ – коэффициент сцепления; f _СОПР – коэффициент сопротивления.

Ст "•

• —f^ = Gf сопр + -V ,                                                       (2)

• 3.    При равномерном повороте вокруг ЦТ сила тяги на каждой из гусениц одинакова, но направлена в противоположные стороны:

g

•• где g – ускорение силы тяжести; V – ускорение машины. То есть коэффициент сцепления боль-

•• ше коэффициента сопротивления на величину, пропорциональную ускорению трактора V .

HGL^ff

GJС^Ц   Gf СОПР + 4 B ’ где µ – коэффициент сопротивления повороту; L – продольная база машины; B – поперечная база машины. Как и в предыдущем случае, сцепление должно быть больше сопротивления. Хотя движение установившееся, но постоянный поворот вносит сюда квазидинамику, связанную с постоянной сменой направления движения. Постоянно действуют центробежные силы от тяг гусениц и центростремительные силы от грунта.

Сократим все слагаемые на — и примем соотношение -^ = 2, что справедливо для большин- ства ГМ. Получим:

• ^fc _U = f сопр ⁺ Ц .                                                                (4)

Преобразуем (4) и введем коэффициенты буксования в повороте δ _ПОВ и при прямолинейном движении δ _ПР

^ ПОВ _ ^f СЦ = 1 + ^Ц δ ПР     f СОПР        f СОПР

.

В результате получаем, что буксование при повороте больше буксования в прямолинейном

Ц

движении в 1 +

раз.

V ^J сопр у

Анализ литературных источников [10–19] (табл. 1, 2) свидетельствует о том, что это соотношение может иметь величину до 10 раз для разных грунтов.

Таблица 1

Коэффициенты сопротивления прямолинейному движению

Грунт	f
Асфальт	0–0,2
Сухая грунтовая дорога	0,03–0,04
Грязная грунтовая дорога (влажность 20 %)	0,09–0,12
Луг	0,05–0,07
Песок	0,12–0,17
Снег	0,07–0,22

Таблица 2

Коэффициенты сопротивления повороту

Грунт	Р тах
Сухой дернистый суглинок	0,8–1,0
Сухая грунтовая дорога на суглинке	0,7–0,9
Пахота на суглинке	0,6–0,8
Влажный суглинистый грунт	0,3–0,4
Снег	0,25–0,7

Таким образом, нет ничего удивительного в том, что кинематические показатели поворота гусеничной машины вокруг вертикальной оси, проходящей через центр тяжести, посчитанные по кинематике трансмиссии и механизма поворота, при полевых испытаниях гусеничной машины существенно искажаются буксованием – в гораздо больших размерах, нежели при прямолинейном движении. Естественно, что 2 % можно пренебречь, а 20 % – уже нельзя!

Выводы:

• 1.    Развита теория движения гусеничных машин в повороте в части определения коэффициента буксования при повороте.

• 2.    Определена аналитическая зависимость между буксованием гусениц в прямолинейном движении и в повороте. Показано, что буксование при развороте трактора вокруг центра тяжести может быть в 10 раз больше аналогичного показателя прямолинейного движения.

• 3.    Результаты справедливы для любых радиусов поворота и зависят от свойств грунта, в частности, от величины коэффициента сопротивления повороту по А.О. Никитину.

Работа выполнялась при финансовой поддержке Министерства науки и высшего образования Российской Федерации в рамках комплексного проекта по созданию высокотехнологичного производства «Разработка бесступенчатого дифференциального механизма поворота со следящей системой управления для внедорожных и дорожно-строительных машин нового поколения» по соглашению № 074-11-2018-006 от 31.05.2018 г. между Министерством науки и высшего образования Российской Федерации и обществом с ограниченной ответственностью «Производственная компания «Ходовые системы» в кооперации с головным исполнителем НИОКТР – Федеральным государственным автономным образовательным учреждением высшего образования «Южно-Уральский государственный университет (национальный исследовательский университет)».