К вопросу выбора минимального состава специализированного программно-аппаратного комплекса и временных интервалов его работы

ВЕСТНИК 2017

Согласно литературным данным, при разработке РЭС различного назначения при учете влияния среды распространения используют, как правило, среднестатистические данные о ее пространственно-временны́ х характеристиках, которые по своему значению относятся к спокойным или, в крайнем случае, слабо возмущенным условиям. Согласно [1], различают спокойное, слабо возмущенное, возмущенное и сильно возмущенное состояние среды распространения. Индикатором возмущенности служат значения индексов геомагнитной активности (Кр, Dst, АЕ и др.), солнечной активности (W, F10.7 и др.), ионосферной возмущенности (Δf0F2). На наш взгляд, для непосредственного использования наиболее подходящими для описания возмущенного состояния ионосферы подходят индексы геомагнитной возмущенности, т.к. изменения W и F10.7 характеризуют изменения солнечной активности, которая, в ряде случаев, может не иметь проявления в приземной атмосфере (так называемые негеоэффективные солнечные возмущения) и, соответственно, не найти своего проявления в изменениях параметров среды распространения. Ионосферные индексы, по сравнению с геомагнитными, для своего получения требуют более сложной процедуры сбора исходных данных и расчета и – соответствующей аппаратуры (в виде станций вертикального, возвратно-наклонного или наклонного зондирования, использования GPS/ГЛОНАСС-приемников). Кроме того, ча- сто возникают ситуации, когда невозможно использование автоматического распознавания высотно-частотного хода слоев ионосферы для определения их параметров и требуется присутствие квалифицированного оператора для разрешения возникшей ситуации. Процедура расчета К-индекса менее сложна, и, кроме того, часто при оценке возмущенности среды требуется оценить динамику изменения геомагнитного поля, а не его абсолютное значение, и аппаратура регистрации позволяет полностью автоматизировать этот процесс [2]. Кроме того, геомагнитное поле более чувствительно к изменению солнечной активности и проявлению ее геоэффективности, а в силу его более раннего взаимодействия (магнитная оболочка магнитосферы) с параметрами солнечного ветра первым реагирует на воздействие солнечного ветра.

Для принятой классификации условий функционирования в табл. 1 приведены диапазоны изменения индексов и ионосферных параметров, характерные для выбранных уровней воз-мущенности.

В табл. 2 приведено значение частоты появления разных уровней возмущенности среды распространения при оценке его по параметру Кр-индекса.

В табл. 3 приведено распределение уровней возмущенности (%) для условного 11-летнего цикла солнечной активности, определенное по значениям ∑Кр за предшествующие годы.

Обобщенные характеристики возмущенности среды распространения

Уровень возмущенности	Тип индекса
	W	S	F А 10,7	Кр	∑ Kp	АЕ	Dst	∆ f o F 2
Спокойные условия (1)	0 – 10	0 – 167	<85	0 – 2	0 – 18	< 190	< 160	± 10 ± 15
Слабо возмущенные условия (2)	11 – 50	168 – 835	< 120	3 – 4	19 – 31	< 370	< 230	± 11–15 < ±20
Умеренно возмущенные условия (3)	51 – 100	836 – 1670	< 160	5 – 6	32 – 44	< 736	< 320	± 16- 20 < ± 30
Сильно возмущенные условия (4)	101 – 150 и более	1671 – 2505	> 160	7 – 9	45 и более	> 737	> 321	> ± 20 > ± 30

Примечание:

W – относительные числа солнечных пятен, или числа Вольфа;

S – сумма площадей солнеч ных пятен, наблюдаемых на всем диске Солнца или их исправленные значения (исправленные значения площади пятен выражают в миллионных долях полусферы Солнца);

F _10,7 – поток радиоизлучения на длине волны 10,7 см, меняется с циклом солнечной активности почти вдвое, величину потока радиоизлучения измеряют в «солнечных единицах потока» – 10^-22 Втм ² Гц ^-1;

К p – трех часовой индекс геомагнитной активности, выражается в баллах – от 0 до 9;

ВЕСТНИК 2017

∑ Kp – суммарный (суточный) индекс геомагнитной активности;

АЕ – мера геомагнитной активности в высоких широтах;

Dst – индекс геомагнитной активности в экваториальной зоне во время магнитосферной бури ( АЕ и Dst измеряются в гаммах);

∆ f 0 F ₂ – вели чиной отклонения критической частоты слоя F ₂( f 0 F ₂) от нор мальных значений, характеризующих спокойное состояние (измеряется в % от скользящей медианы F ₂, в числителе приведены полусуточные значения ∆ f 0 F ₂, в знаменателе – ежечасные).

Частота появления уровней возмущенности по значению Кр-индекса

Распределение уровней возмущенности

Таблица 2

Частота (р) появления уровней возмущенности среды распространения по значению Кр-индекса	Уровень возмущенности
0,534	1
0,361	2
0,0892	3
0,0158	4

Таблица 3

Уровень возмущен-ности	Условный 11-летний цикл солнечной активности
	Мин. СА   Подъем СА        Макс. СА       Спад СА       Мин. СА
	1	2	3	4	5	6	7	8	9	10	11
1	66	67,3	44,1	43	43,3	36,4	35,6	60,8	58,5	62,2	70,1
2	31,2	29	42,7	41,9	41,3	45,7	45,7	30,9	32,8	29,4	26,8
3	2,8	3,7	10,9	11,7	13,1	14,5	15	6,5	8,7	7,9	3,1
4	–	–	2,3	3,4	2,3	3,4	3,7	1,8	–	0,5	–

ВЕСТНИК 2017

Как следует из приведенной таблицы, спокойное и слабо возмущенное состояние среды распространения (уровень возмущенности 1 и 2) составляет, в зависимости от фазы солнечной активности, от 81,3 до 97,2%. В соответствии с этим, большинство получаемых при проведении различного рода измерений и научных наблюдений (кроме специально организованных измерений, например в период Международного геофизического года или в год спокойного Солнца) среднестатистических характеристик среды распространения будут соответствовать спокойному (или, в крайнем случае, слабо возмущенному) состоянию ионосферы. Исходя из того что в этих условиях параметры ионосферы достаточно хорошо описываются детерминированной моделью ионосферы, может сложиться мнение, что на достаточно большом интервале времени нет необходимости оперативной корректировки параметров используемой модели.

Для проверки достоверности данного высказывания кратко рассмотрим временные характеристики изменения состояния среды распространения (в нашем случае – ионосферы) в спокойных условиях. При этом в качестве уровня ее возмущенности будем использовать параметр Δ f ₀ F ₂, а в качестве критерия ее влияния – величину ошибки по дальности Δ R , которая связана с полным электронным содержанием (ПЭС)

на трассе распространения «радиоэлектронное средство – среда распространения (ионосфера) – цель» следующим соотношением

∆ R =

40,3 f ²

h 2

TEC, где ТЕС = J N e ( l ) dl.

h i

Определенный интерес представляет знание вариаций ПЭС для принятых уровней возмущен-ности. Ввиду отсутствия в доступной литературе достаточной статистики по вариациям ПЭС при различных уровнях возмущенности среды распространения, воспользуемся следующим экспериментально полученным эмпирическим выражением

ПЭС [ TECU ]

f о F 2 =

2.088 + 0.0447* ПЭС’

[МГц].

Данное выражение было получено на основании анализа вклада той или иной части ионосферы, высотный ход которого приведен на рис. 1. На этом рисунке приведен дифференциальный вклад составляющей высотного хода распределения электронов в ПЭС (дифференциальное значение ПЭС, выраженное в ТЕСU, где TECU = 1*1016 эл/м2). Из данного рисунка следу- ет, что основной вклад в ПЭС дает электронная концентрация (Ne) области F2 ионосферы, приходящаяся на максимум Ne этой области (hmF2 на рисунке соответствует положению высоты максимума Ne, с которым связано значение f0F2).

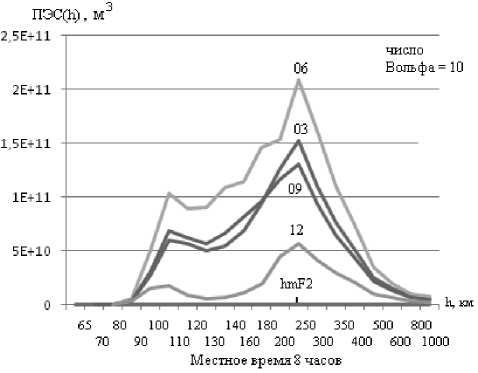
а)

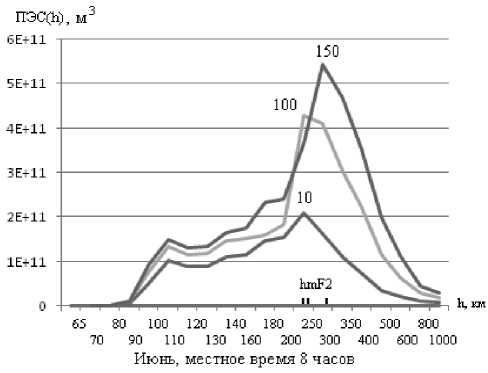
б)

Рис. 1. Дифференциальный вклад F-области ионосферы в значение ПЭС.

На рисунке а) цифрами обозначены порядковые номера месяца года, а на рисунке б) – уровни солнечной активности в числах Вольфа

Значение электронной концентрации связано со значением критической частоты ( f ) следую-щимвыражением: N_e [ см ^{- 3}] = 12400 • f ²[МГц] . Таким образом, зная значение N _e (в частности, в максимуме области F ₂ ионосферы), можно определить значение критической частоты для этой области ( f ₀ F ₂) и через приведенное выше эмпирическое выражение – значение ПЭС:

_{ПЭС =} 2,088 ⋅ f 0 F 2                (1)

1 - 0.0447 ⋅ f ₀ F ₂

Используя выражение (1), получим размах вариаций ПЭС для разных пределов изменения Δf0F2 и тем самым оценим в первом приближении изменение ПЭС для принятой градации уровней возмущенности. Оценку будем прово- дить для типовых ночных и дневных значений критической частоты f0F2: 3,5 МГц для ночных и 15 МГц для дневных условий. Результаты оценки приведены в таблице 4.

Таблица 4

Вариации ПЭС для разных уровней возмущенности и соответствующих им вариациям Δ f ₀ F ₂

Известно, что за основной критерий ионосферной возмущенности принимается величина отклонения (в %) критической частоты слоя F ₂ за данный час от скользящей медианы за тот же

час, что исключает влияние суточного и сезонного ходов [3] на величину Δ f ₀ F ₂

A f о F 2 =

f0 F2   f0 F2 ск.мед f0F2 ск.мед

■ 100 %.

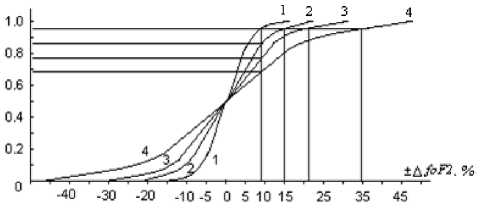
Рис . 2. Интегральное распределение Δ f₀F₂ для разных уровней возмущенности ( цифры 1…4 соответствуют уровням возмущенности в соответствии с таблицей 1)

Статистический анализ распределений Δ f ₀ F ₂, по данным ряда ионосферных станций, показал,

что спокойному состоянию ионосферы соответствует распределение Δ f ₀F₂, в первом приближении подчиняющееся закону Гаусса [3]:

ВЕСТНИК 2017

( x - m ) ²

P ( x ) = — e 2 " ² , ^v   "in

где Р(х)– частота появления Δ f₀F₂ в выбран ном интервале ; m – математическое ожидание ; σ – среднеквадратичное отклонение нормально распределенной случайной величины . В нашем случае заданные граничные изменения Δ f₀F₂ для того или иного уровня возмущенности могут быть использованы как максимальные значения размаха в ±3σ для данного вида распределения . С учетом сказанного были построены инте гральные нормированные распределения Δ f₀F₂ ( рис . 2) для каждого из 4- х уровней возмущенно - сти с учетом данных таблицы 1. Далее была про ведена оценка изменения вероятности выполне ния требования обеспечения заданного уровня условной ошибки ( в нашем случае по дальности ∆ R) при разных уровнях возмущенности . Не на рушая общности подхода , было принято , что в спокойных условиях ( уровень возмущенности 1) заданная условная ошибка ( ее непревышение ) выполняется в 95% случаев .

Анализ рис . 2 показывает , что если для спо койных условий ( в соответствии с принятой гра дацией ) процент невыполнения соответствует значению 5%, то для уровней 2, 3 и 4 этот про цент невыполнения будет составлять 14, 23 и 32% соответственно . Для корректного учета « веса » влияния того или иного уровня возмущенности было оценено комплексное влияние вероятности невыполнения требования заданной условной ошибки по дальности с учетом состояния среды распространения радиоволн ( частоты появления того или иного уровня возмущенности ). В табл . 5 приведены относительная частота появления уровня возмущенности , относительное значение невыполнения требования по заданной условной ошибке определения дальности и произведение относительной частоты состояния среды распро странения на величину невыполнения условной ошибки по дальности : q_i = p_i*a_i.

Анализ данных таблицы 5 показывает , что наибольший ранг (« вес » невыполнения ) при ходится на слабо возмущенные условия , сле дующими идут спокойные условия . Данное обстоятельство говорит о том , что и в спокой -

Уровни возмущенности	Интервалы вариации Δ f0F2, %	Интервалы вариации ПЭС , %
		ночь	день
Спокойные условия (1)	± 15	± 5,1	± 3
Слабо возмущенные условия (2)	<± 20	± 6,8	± 4,04
Умеренно возмущенные условия (3)	<± 30	± 10,1	± 6,08
Сильно возмущенные условия (4)	± 40	± 13,5	± 8,11

Значения относительных частот состояния среды распространения и относительных частот невыполнения заданных требований

Средняя частота ( p ) появления уровней возму-щенности среды распространения радиоволн ( i = 1…4) в 11-летнем цикле солнечной активности		Относительное ( а ) значение невыполнения требования заданной ошибки	Значение q = p * a
p (Кр)	i	а	q	Ранг
0,534	1	0,05	0,0267	2
0,361	2	0,14	0,05054	1
0,0892	3	0,23	0,020516	3
0,0158	4	0,32	0,000249	4

ВЕСТНИК 2017

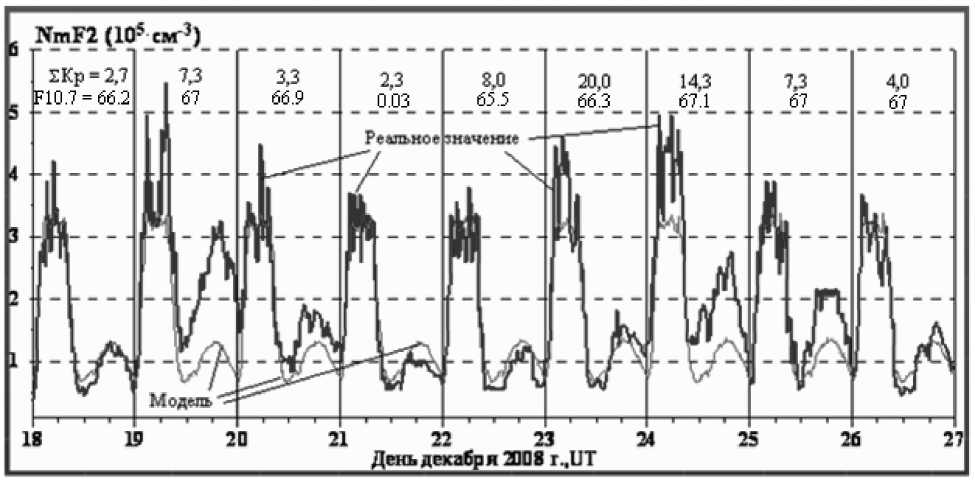
Рис. 3. Вариации электронной концентрации в максимуме области F ₂ ионосферы ( N_еmF ₂ = 12400* f ₀ ² F ₂)

ных условиях (в силу их наибольшей частоты появления – 53,4% от общего времени работы средства) необходим оперативный учет текущего состояния среды распространения, особенно это касается средств и систем, работающих в масштабе времени, близком к реальному. Для подтверждения сказанного, рассмотрим динамику изменения f ₀ F ₂ (рис. 3, данные Института солнечно-земной физики СО РАН).

Представленный на рисунке временной отрезок с 18 декабря по 26 декабря 2008 г. характеризуется отсутствием солнечных вспышек, геомагнитных возмущений (максимальное значение индекса магнитной активности за данный период составило Крmax = 3.7, ∑Кр = 20.0, минимальное значение интенсивности излучения на длине волны 10.7см составило F10.7min = 0.03, максимальное – 67.10). Указанные данные свидетельствуют о спокойных условиях, в которых были получены данные, приведенные на этом рисунке. Однако анализ отклонений Δf0F2 от модельного значения в ряде случаев был значительным и достаточно продолжительным. На рис. 4 представлено интегральное распределение Δf0F2 для рассматриваемого периода (кривая 2).

Видно, что по своему значению отклонения Δf0F2 выходят за рамки границ отклонений, соответствующих градации спокойного состояния ионосферы (кривая 1, рис. 4 и рис. 2), и выполнение заданного значения условной ошибки выполняется лишь для 68% (кривая 2, рис. 4) данного как бы спокойного по всем параметрам геофизических геомагнитных и солнечных индексов состояния среды распространения.

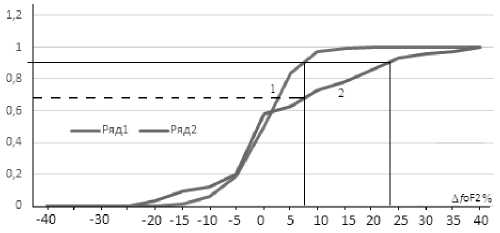
Рис. 4. Интегральное распределение Δ f ₀ F ₂ для обобщенно статистических спокойных условий (1) и для рассматриваемого интервала в декабре 2008 года (2)

Приведенные данные свидетельствуют о том, что и в спокойных условиях используемая математическая модель среды нуждается в корректировке. При этом надо понимать, что значение условной ошибки может лежать и в другом интервале отклонений (например, ближе к нулевому значению интегрального распределения). В этом случае корректировка используемой математической модели среды будет нуждаться в корректировке в еще бóльшем интервале времени (если не постоянно).

Как видно из представленного рисунка, для рассматриваемого спокойного интервала требуемая условная ошибка по дальности будет выполняться в 68% времени, а в оставшихся 27% (в сумме – требуемые 95%) она будет превышать заданную условную ошибку по дальности. Используя полученное на рис. 4 превышение по Δ f ₀ F ₂, зависимость ПЭС от f ₀ F ₂ (выражение 1) и

∆ R = f (ПЭС), получим, что ожидаемая ошибка по дальности превысит заданную условную ошибку по дальности в 1,16 раза.

Следующим немаловажным значением является темп корректировки используемой модели среды распространения (темп измерения параметров среды, используемых для последующей корректировки модели среды).

Критерием выбора темпа обновления входных данных по среде может служить требование – непревышение заданной ошибки траекторных измерений (т.е. постоянство заданной ошибки измерений). Выполнение данного критерия в первом приближении требует практически постоянной по времени корректировки используемой модели среды распространения. Однако, используя пространственный и временной радиусы корреляции параметров среды распространения, по которым осуществляется корректиров- ка (это значение ПЭС для ионосферы и значения температуры, давления и влажности, определяющие коэффициент преломления в тропосфере), можно оценить минимальный темп обновления указанных параметров. В первом приближении в качестве ухудшения качества работы схемы адаптации можно взять следующее. В работе [4] показана степень компенсации влияния среды распространения для следующих случаев: отсутствие учета влияния среды, использование детерминированной модели среды и использование корректируемой по измеренным параметрам среды распространения указанной детерминированной модели. На рис. 5 приведены экспериментально полученные интегральные нормированные функции распределения невязки по дальности для указанных случаев.

Для расчетов использовались данные траекторных измерений РЛС дальнего обнаружения дециметрового диапазона по спутникам юстировочного класса. Всего было получено около 2000 единичных измерений в течение 27–29 марта 2014 года.

Эмпирическая функция распределения нормированной невязки по да/ъности

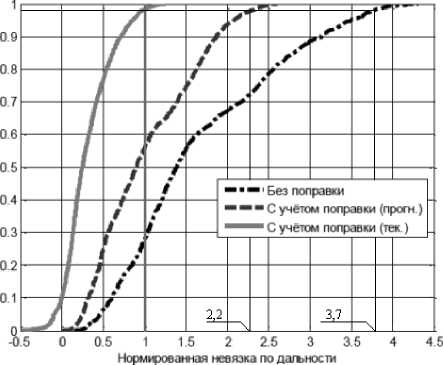
Рис. 5. Интегральные нормированные функции распределения невязки по дальности

ВЕСТНИК 2017

Геомагнитная обстановка в указанный период была спокойной, минимальное значение индекса Dst составило –22 нТ. В первом случае строилась интегральная функция распределения невязок без компенсации атмосферных ошибок, на рисунке она обозначена «Без поправки». Фактически этот случай соответствует реальному распределению текущих ошибок измерения рассматриваемых параметров без какого-либо учета условий распространения.

Во втором случае вводились поправки, рассчитанные по модели ионосферы с учетом прогнозного значения солнечных пятен W, но без коррекции модели по данным текущих измере-

ВЕСТНИК 2017

ний наклонного ТЕС – обозначение «С учетом поправки (прогн.)».

В третьем случае вводились поправки, рассчитанные по модели ионосферы с учетом ее коррекции по данным текущих измерений наклонного ТЕС – обозначение «С учетом поправки (тек.)».

Анализ результатов, представленных на рис. 5, позволяет сделать следующие выводы.

• 1.    Без использования каких-либо поправок большая часть невязок значительно превышает требуемое пороговое значение по дальности – в 72% случаев (в нашем случае нормированное пороговое значение невязки равно 1).

• 2.    Внесение поправок, рассчитанных на основе модели ионосферы без коррекции, позволяет повысить точность единичных измерений. При этом общий процент измерений, превышающих требуемое пороговое значение невязки, уменьшается и составляет по дальности 45% случаев.

• 3.    Использование поправок, рассчитанных на основе скорректированной модели ионосферы, позволяет значительно повысить точность единичных измерений РЛС по дальности: число измерений, превышающих пороговое значение невязки, сократилось в рассматриваемом случае до 2%.

Используя указанные цифры, определим темп измерения и последующей корректировки используемой детерминированной модели среды по этим измеренным параметрам при снижении (увеличении нормированной невязки по дальности) в 2,2 и 3,7 раза для случая использования некорректируемой модели среды и отсутствия учета влияния среды вообще, соответственно.

В качестве изменения параметров ионосферы будем использовать данные по вариациям ПЭС и изменения критической частоты области F ₂ ионосферы в периоды ионосферных возмущений [5–8], изменения электронной концентрации в спокойной ионосфере (рис. 3) и изменения параметров тропосферы при резком изменении метеопараметров [9].

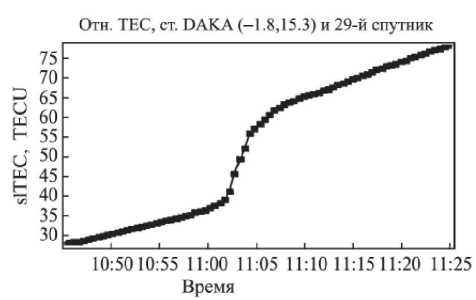
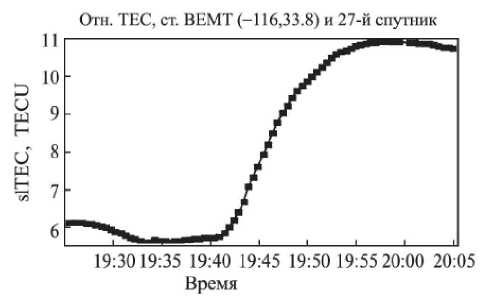
Изменения ПЭС в периоды ионосферных возмущений [8]. Согласно этим данным, динамика изменения ПЭС для рассматриваемых случаев имела вид, представленный на рис. 6.

Согласно данным рис. 6, относительное максимальное увеличение ПЭС составило порядка 40 TECU на интервале примерно 40 минут во время вспышки 28.10.2003 г. и около 5 TECU на интервале 15 минут – 04.11.2003 г. Видно, что имеет место достаточно резкое увеличение ПЭС (эффект внезапного увеличения электронного содержания (SITEC)).

а) 28 октября 2003 г.

б) 4 ноября 2003 г.

Рис. 6. Изменение ТЕС для пар спутник GPS – приемник GPS в периоды интенсивных солнечных вспышек 28 октября и 4 ноября 2003 г. [8]

Исходя из максимального изменения ПЭС на указанных временных интервалах и принимая линейный закон изменения ПЭС, оценим изменение (прирост) ошибки по дальности в связи с изменением ПЭС. На рис. 7 для рассматри- ваемых временных интервалов максимального изменения ПЭС представлены относительные изменения ∆R. Оценку требуемого временного интервала оценки текущего ПЭС для корректировки траекторных измерений проводили исходя из следующих допущений. Согласно данным рис. 5, максимально допустимая нормированная ошибка для случая корректировки модели ионосферы (невязка) составляет 1,2 от ее допустимого нормированного значения по уровню 0,98 (в нашем случае 1).

Считая, что на момент начала возмущения скорректированная нормированная ошибка соответствовала значению ПЭС (ПЭС = TEC = 32, рис. 6а) на начало возмущения, то, используя со- отношение

40 3

Δ R = ^{40, 3} ПЭС, f ²

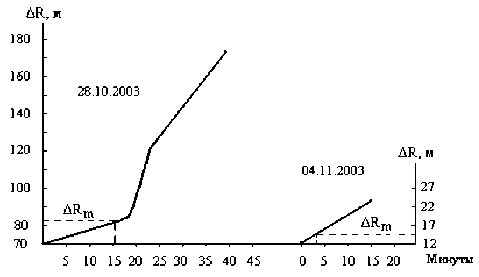
Рис. 7. Изменение ошибки по дальности ∆R получаем, что нормированная ошибка (невязка) будет равна ~70 метров в дециметровом диапазоне длин волн, а максимально допустимая ошибка в этом случае будет равна ∆Rm = ∆R70*1,2 = 84 метра. Максимальная ошибка за время изменения ПЭС на 40-минутном интервале в период возмущения 28.10.2003 года будет составлять 176 метров.

Аналогичные расчеты были проведены и для резкого изменения ПЭС 04.11.2003 года. При этом считалось, что при достижении ошибки, равной ∆ R_m = 1,2*∆ R , должны происходить обновления исходных данных по среде распространения и соответствующая очередная корректировка модели ионосферы. Указанные моменты изменения приведены на рис. 7 пунктирной линией. Из данного рисунка следует, что темп обновления исходных данных по среде должен составлять в периоды возмущений от 3 до 15 минут. Однако, учитывая отсутствие оперативной информации о состоянии среды (о наличии возмущения и резкого изменения ПЭС), с одной стороны, и более частого появления возмущений с малыми вариациями ПЭС на временных интервалах 15–20 минут, с другой стороны, представляется целесообразным (при наличии информации о резком изменении ПЭС) темп обновления делать равным 3 минутам.

Анализ изменений электронной концентрации в спокойных условиях, приведенный на рис. 3, при рассмотренном выше подходе показал, что темп обновления текущих измерений параметров среды распространения (в нашем случае ПЭС) в спокойных условиях колеблется от 45 до 210 минут.

В работах [4; 10] показано, что в периоды восходно-заходных явлений (при прохождении терминатора на высотах тропосферы в зоне ответственности РЛС ДО [4; 11]), а также резкого изменения метеоусловий (например, дождь – рис. 8 [9]) происходит существенное уменьше- ние радиуса временной корреляции до единиц минут, что соизмеримо с временным радиусом корреляции в ионосфере.

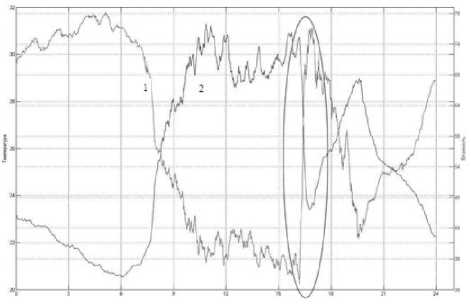
Рис. 8. Аномальный суточный ход температуры (1) и относительной влажности (2) воздуха

Данное обстоятельство позволяет сделать вывод, что в периоды существенного изменения параметров среды распространения необходимо уменьшение (по предварительным оценкам до 3-х минут) временного интервала текущего обновления (измерения) соответствующих параметров среды распространения, используемых для оперативной коррекции модели среды, используемой при траекторных измерениях в РЛС ДО.

Проведенный анализ учета тропосферы и ионосферы на распространение радиоволн УКВ-диапазона позволил сформулировать требования к первичному составу аппаратных средств и программного обеспечения специализированного программно-аппаратного комплекса. В его состав должны входить автоматическая метеостанция для измерения в текущем масштабе времени температуры, давления и влажности приземного воздуха и GPS/ГЛОНАСС-приемник для измерения ПЭС. При выборе приемника можно воспользоваться рекомендациями работы [12], где проведен сравнительный анализ устойчивости работы ряда GPS-приемников в различных геофизических условиях. Что касается специального программного обеспечения, то наряду с программным обеспечением по обработке текущих измерений указанных выше параметров среды распространения, в указанном комплексе должны присутствовать локальные математические модели тропосферы и ионосферы в зоне ответственности РЛС ДО, математическая модель распространения радиоволн, программное обеспечение увязки параметров среды (модели среды) с ПО канала обработки целевой информации (см. например, [13; 14]). Указанное программное обеспечение должно быть реализовано на языке, предусмотренном Заказчиком средств, на

ВЕСТНИК 2017

ВЕСТНИК 2017

которых предполагается размещение рассматриваемого специализированного программноаппаратного комплекса геофизического обеспечения (в нашем случае – на языке С/С++).

Выводы

• 1.    Проведенный анализ показал, что используемые математические модели среды распространения в основном описывают спокойное или слабо возмущенное состояние среды распространения.

• 2.    В интересах уменьшения влияния среды распространения необходима корректировка используемой модели среды распространения по ее текущим измеряемым параметрам. Оценки показали, что первоочередная корректировка необходима при функционировании средства (в нашем случае радиолокационной станции дальнего обнаружения (РЛС ДО)) в условиях слабо возмущенной среды распространения. Однако для РЛС ДО, работающей в реальном или ква-зиреальном времени, указанная корректировка параметров используемой модели среды распространения требуется постоянно, вне зависимости от текущего состояния среды распространения.

• 3.    Условия необходимости корректировки и темп обновления информации о текущем состоянии среды распространения определяется критерием постоянства заданной ошибки измерения параметра, определяющего качество функционирования измерительного средства.

• 4.    Специализированный программно-аппаратный комплекс текущих измерений параметров среды распространения минимального состава должен включать автоматическую метеостанцию для измерения в текущем масштабе времени температуры, давления и влажности приземного воздуха и GPS/ГЛОНАСС-приемник для измерения ПЭС. Специальное программное обеспечение должно быть написано на языке С/С++ и состоять из математических локальных моделей тропосферы, ионосферы, модели распространения радиоволн, алгоритмов сопряжения выхода специализированного программно-аппаратного комплекса с каналом целевой обработки РЛС ДО.