К возможности перехода от практики приближенного к точному определению деформаций тканей, одежды

Для обоснования требований, предъявляемых к различным изделиям, одежде, отвечающих по удобству, комфорту, дизайну и иным характеристикам, в частности, конструктивно-технологическим припускам, необходимы сведения о деформациях, происходящих в материалах, одежде. Из изучения и анализа известных источников такие сведения по деформациям, их определению, учету крайне ограничены.

Как известно, одежда создается с учетом формы и размеров фигуры человека, но не является точной ее копией. Степень прилегания одежды на разных участках фигуры неодинакова. На участках опорных поверхностей, между одеждой и телом человека, существуют воздушные зазоры, которые необходимы для обеспечения свободы дыхания и движений, нормальной жизнедеятельности человека. На практике при конструировании одежды размерные признаки, полученные путем измерения конкретной фигуры человека или взятые из таблиц антропометрических измерений типовых фигур, составляют лишь часть измерения соответствующего участка одежды.

Объект и методы исследования

Рассмотрим теорию и практику использования одной из известных математических моделей определения деформаций тканей и одежды - «чебышевскую сеть», возможность уточнения, поскольку предварительное изучение показало ее приближенный характер.

В работе «О кройке одежды» [1] русский математик П.Л. Чебышев доказал возможность построения разверток плотно облегающих оболочек из ткани для различных поверхностей. При этом он исходил из того, что нити основы и утка ткани в ее первоначальной плоской форме пересекаются между собой ортогонально и при одевании поверхности ткани изменяются только углы между нитями, а длина нитей остается прежней. Чебышев также допускал, что при изменении прямоугольных ячеек ткани в параллелограммы ткань оказывает сопротивление при растяжении ее только вдоль нитей основы и утка. Соответственно, в оболочке из ткани, плотно облегающей поверхность, нити основы и утка натянуты силами, действующими вдоль их длины и для того, чтобы натянутые нити на поверхности находились в равновесии, они должны располагаться по геодезическим линиям. Это известное условие равновесия нитей на поверхности в общем случае может быть строго выполнено только одной нитью основы и одной нитью утка, так как направление всех нитей ткани не совпадает с геодезическими линиями. Поэтому, чтобы обеспечить равновесие нитей ткани на поверхности, Чебышев пришел к необходимости расположения двух пересекающихся нитей ткани по ортогональным геодезическим линиям. Он принял их за исходные оси координат на поверхности (х, у), считая координатами длину нитей основы и утка ткани (рис.1).

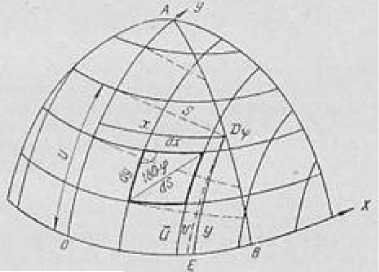
Рисунок 1 - Оболочка из ткани на поверхности

При этом, нити ткани Чебышевым рассматриваются как координатные линии, образующие на поверхности криволинейную чебышевскую сеть, элементами которой являются бесконечно малые параллелограммы. Длина диагонали элементарного параллелограмма, как известно, равна

ds = JV(dy2 + dx2 + 2cosфdydx  (1)

и определяет расстояние между двумя соседними точками поверхности (рис. 1). Исходя из этого уравнения, Чебышев решил поставленную задачу об одевании поверхности тканью в виде следующих формул:

x = S + 1/6(k o ²u² + k o k 2 u³ + 1W)S3 + 1/8(k o k i u2 + 1/2k i k 2 U³)S⁴ + .. .

у = u - (1/2k 0 u + 1/4k 2 u²)S² + 1/6k 1 uS³ + . . .,                            (2)

где: х и у - прямоугольные координаты, определяющие форму развертки оболочек из ткани на плоскости; S - кратчайшее расстояние от оси Оy до точек линии шва (границы) оболочки на поверхности (рис. 1); u – ордината точки пересечения линией кратчайшего расстояния - (S) оси Оy; k0, k2, k3 – коэффициенты разложения в степенной ряд гауссовой кривизны поверхности в данной точке (х, у).

Чтобы проверить указанные формулы, Чебышев определил по ним форму развертки оболочки для шара, состоящей из двух частей, и нашел простой способ ее построения дугами окружностей радиусов r и R (рис. 2).

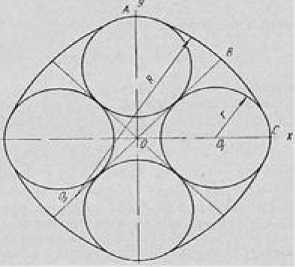
Рисунок 2 - Развертка оболочки для шара из двух частей

Эти радиусы определяются по формулам: r = 0,65Rш; R = 2,46Rш,       (3)

где Rш - радиус шара при АВ = ВС; ОА = ОС = 0,5πRш; ОВ = 1,42Rш.

Раскрой оболочки производят, располагая нити основы и утка ткани по осям координат Ох, Оу.

Результаты и их обсуждение

Экспериментальная проверка оболочек из разных тканей (канвы, бортовой парусины, шерстяных костюмных тканей) свидетельствует о возможности изготовления по разверткам Чебышева плотно облегающей оболочки из ткани для поверхности шара, состоящей из двух частей. Но, как известно, размеры человеческого тела не являются строго определенными и в динамике с течением времени, как относительно больших интервалов (месяцев, недель, дней), так и коротких, например, при дыхании (минуты, секунды) – изменяются. Причем, эти изменения следуют не только во времени, но и в пространстве, т.е.

являются объемными и/или линейными, нелинейными и, кроме того, в разных частях тела изменяются по-разному. Таким образом, начальный размер тела L 1 на момент времени t 1 отличается от размера на другой момент времени, например, в t 2 - до L 2 , на величину ∆L

∆L= L 2 -L 1 (4)

Выражение (4) является алгебраическим, поскольку в нем ∆L может быть, как положительное (при растяжении), так отрицательным (при сжатии, усадке). То есть, в любой момент времени

L= L 0 ± ∆L, (5)

где L 0- - первоначальный до изменения размер.

В свою очередь, любому текстильному материалу присуща деформация, т.е. изменение размеров. Напомним, что деформация происходит в основном под воздействием внешних сил; точки материала меняют положение в пространстве. Величина изменения характеризуется линейными и угловыми пе- ремещениями в материале, что приводит к искажению его формы и изменению размеров. Деформация может быть как однородной, так и неоднородной, но в любом случае, зависящей от многих факторов, например, температуры, влажности тела и окружающей среды и др., и, конечно, зависит от вида, типа материала, его качества, свойств, особенностей. Для эластичных материалов, в которых присутствует синтетика, она больше, для натуральных материалов - меньше. Также деформации зависят не только от физических свойств материалов, но и от их геометрических размеров, структуры, исходного сырья (ниток) и т.д.

В разное время были предложены различные определения деформаций. Математическим моделям аналитического определения главных деформаций (на растяжение) посвящено множество работ, в том числе выдающихся математиков: Лагранжа, Эйлера, Коши и др. [4,5]. Основное различие в них, как будет показано ниже, состоит в принятых переменных и их кратности.

Пусть отрезок материала имеет длину 1 о. В результате однородной деформации растяжение его длины становится равным 1 1. Тогда, определение относительной деформации Е в переменных Лагранжа (1 о., 1 1 ) , будет:

Е = (1 1 -1 о ) / 1 о =А1/ 1 о (6)

Пока деформация мала, определение ее не зависит от того, относить ли к начальной длине или конечной. Деформация, отнесенная к конечной длине отрезка, равна

£ = А1 / 1 1 = £ / ( 1 + Е _) = £ - £ 2 +—, (7)

где £ - лагранжева деформация, вычисленная по формуле (6).

Разница между £ и является величиной второго порядка и ею, в случае Е <<1, можно пренебречь. Для больших деформаций становится не безразлично, к какой именно длине относить удлинение отрезка. Вычисленная зависимость величины деформации от способов ее аналитического определения, иллюстри -руется на рис. 3.

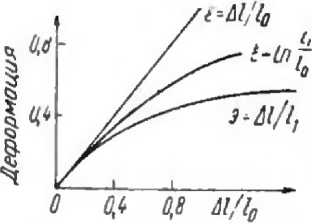
Рисунок 3 - Зависимость величины деформации от способов ее определения

Перечисленные выше способы вычисления деформации не являются единственными и наиболее удобными. В разное время были предложены различные определения деформаций. Основные из них представлены в таблице 1 (колонка 2). Что касается выражений в колонке 4, то они найдены авторами с использованием тензорного анализа. Причем, в данной работе основному понятию тензорного анализа - пространству, как дифферен циально-геометрическому многообразию, уделено существенное внимание и принято, что тензор деформации — такой тензор, который характеризует сжатие (растяжение) и изменение формы в каждой точке тела при деформации. То есть, тензор — это математический объект, который не зависит от смены системы координат, но его компоненты при их смене преобразуются по определенному математическому закону.

Таблица 1 - Формулы для различных определений деформаций

Название главной деформации	Формула	Название главной деформации	Формула
Лагранжева	(1 1 -1 о ) / 1 о	Лагранжева тензорная	(1 12 -1 о2 ) /21 о2
Эйлерова	(1 1 - 1 ) / 1 1	Эйлерова тензорная	(1 12 -1 о2 ) /21 12
Кратность	1 1 / 1 о	Грина-Сен-Венана тензорная	1 12 / 1 о2
Обратная кратность	1 о /1 1	Алманси-Коши тензорная	1 о2 / 1 12
Логарифмическая	ln(£ c /1 1 )	Комбинированная	(1 12 -1 о2 ) /2£ 1 £ о

Из таблицы 1 можно проследить, что пять из представленных определений деформаций могут быть выражены в виде единой формулы (8).

£ = (1/n) .[1 - (l o / l i )ⁿ ] (8)

Нетрудно заключить из (8), что при значениях n=2, 1, 0, -1,-2 представленные формулы в таблице 1 получены соответственно для эйлеровых и эйлеровых тензорных, лагранжевых и лагранжевых тензорных, логарифмических деформаций.

Решением задачи об одевании поверхностей тканью после Чебышева занимались и другие математики. Однако результаты их исследований не могут быть непосредственно использованы при конструировании одежды вследствие того, что они решали вопросы дифференциальной геометрии, в задачу которой не входит изучение методов определения оболочек из ткани. Вместе с тем, их исследования показывают, что строгое решение задачи об одевании поверхностей приводит к значительным математическим осложнениям. Поэтому решать эту задачу для расчета разверток оболочек из тканей необходимо приближенными методами. Применение этих методов значительно упрощает решение задачи об одевании поверхности и обеспечивает достаточную точность расчета разверток деталей одежды, но, как выяснилось, при условии, что их формование происходит при небольшом угле перекоса нитей ткани (15 - 18°). Координаты, входящие в формулы Чебышева, являются ортогональными геодезическими линиями; их можно определить непосредственным измерением поверхности с помощью геодезического угольника. Но, несмотря на это, формулы Чебышева не использовались при конструировании одежды, так как не были разработаны методы их применения для расчета разверток различных поверхностей. Эти формулы представляют собой степенные ряды, определяющие координаты разверток (х, у). Поэтому для приближенных расчетов формулы (1,2) можно упростить.

Авторами исследовалась возможность определения и учета деформаций различными методами. Основное внимание обращено на два основных метода экспериментального анализа деформаций: муар и делительных (координатных) сеток. Другие изученные нами методы, как правило, имеют ограничен- ное применение, достаточно сложные и /или обладают сравнительно невысокой точностью. В части последнего обстоятельства, то в пользу метода муар и, переходящего его при определенных условиях к делительным сеткам, явилась возможность использования инновационных инструментальных средств определения деформаций на базе передовых сенсорных, цифровых технологий [2,3].

Что касается использования более точных математических моделей определения деформаций в текстильных материалах, тканях, одежде, в том числе, показанных в табл. 1, то результаты их экспериментальной проверки показали близкую сходимость с представленными аналитическими зависимостями на рис.1

Заключение

• 1.    Рассмотрены вопросы существующей теории и практики расчета и назначения припусков тканей, швейных изделий, опирающиеся на известные методы и модели выдающихся математиков: Чебышева, Лагранжа, Эйлера, Коши.

• 2.    Представлены уточненные математические модели определения деформаций в тканях и одежде, результаты их аналитических, экспериментальных исследований. Практические исследования выполнены с использованием инновационных сенсорных, цифровых технологий