К задаче о стабилизации решений уравнения газовой динамики
Автор: Миклюков В.М., Полупанов С.С., Тарапата P.A.
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Математика
Статья в выпуске: 9, 2005 года.
Бесплатный доступ
Указываются границы допустимой скорости стабилизации решений уравнения газовой динамики, при превышении которой решения могут быть лишь тождественно постоянными. Доказательства базируются на технике квазиконформных отображений.
Короткий адрес: https://sciup.org/14968570
IDR: 14968570 | УДК: 517.54
Текст научной статьи К задаче о стабилизации решений уравнения газовой динамики
Указываются границы допустимой скорости стабилизации решений уравнения газовой динамики, при превышении которой решения могут быть лишь тождественно постоянными. Доказательства базируются на технике квазиконформных отображений.
1. Основные результаты
В работе рассматриваются обобщенные решения уравнения вида
где o^q) - непрерывная функция, сг(О) = 1.
При
y(g) = 1 -
7 - 1
1/(7-1)
мы имеем классическое уравнение газовой динамики. Данное уравнение описывает потенциал скоростей плоского установившегося течения идеального газа в адиабатическом режиме; — сю < 7 < +оо — постоянная, характеризующая газ (см., напр., [1, § 15 гл. IV]). Для 7 = 1 ± 0 полагаем
Данное урав нение име ет эллиптический тип пр и 7 < 1. Д ля 7 > 1 оно эллиптично при q < >/2/(7 ~ 1), параболично при q = 1/27(7^1) и гиперболично при q > ^2/(7 —1). Ниже мы предполагаем, что или 7 < 1, или 7 > 1 и
esssupq(x,y) <
7-1
для всякой подобласти D' СС D,
т. е. уравнение (1) является эллиптическим на решении ср.
Последнее означает, что при фиксированном решении ср мы рассматриваем ст как (наперед заданную) измеримую функцию переменной (ж, у), после чего линейное уравнение (1) становится эллиптичным. Решения уравнения (1), в котором весовая
функция а есть функция переменной (ж, у), называются а-гармоническими функциями. Изучению таких функций посвящено значительное количество работ (см., напр., [2], [3] и цитированную там литературу).
Пусть D — область в R2. Для произвольной локально липшицевой функции f : D —> R мы обозначаем через Вь(Г) множество всех точек а Е D, в которых / не имеет полного дифференциала. Согласно известной теореме Радемахера [4, теорема 3.1.6] множество D6(/) имеет нулевую двумерную меру Лебега.
Удобно пользоваться следующим определением обобщенного решения уравнения (1) [5]. Локально липшицева в D функция у? называется обобщенным решением уравнения (1), если для произвольной подобласти △ СС D со спрямляемой границей ЭД, mesi (5Д П D^p^ = 0 1 и для произвольной функции у Е Lip Д выполнено
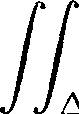
о^ к^хПх + Р^) dxdy = j усг^ ^-p^dx + pxdy). (3) ад
Подчеркнем, что в случае достаточной гладкости решения р соотношение (3) влечет выполнение (1) в традиционном смысле.
В настоящей работе получены теоремы типа Фрагмена — Линделефа, описывающие допустимую скорость стабилизации градиента решения в окрестности граничной точки, при превышении которой решения могут быть лишь тождественно постоянными. В частности, приводится доказательство следующей теоремы, анонсированной в [6].
Теорема 1. Пусть ф —- обобщенное решение уравнения (1) в полуполосе П = {(ж, у) : 0 < х < сю, 0 < у < /г}. Предположим, что при всяком 0 < ж < +оо выполнено
1шнр^ = lim ^(ж,у) = 0, (4)
у—*+0 у—>й—О иу и для некоторого s > ^/h для всех, достаточно больших ж > 0, справедлива оценка ess sup |Х7у?(ж, у)| < exp {—exp {аж}} . (5)
0 Тогда р = 0 в П. Рассмотрим теперь круговой сектор раствора а, 0 < а < 2 тг, D — {(ж, у) Е R2 : 0 < \/ж2 + у2< 1, 0 < arctg — < а}. Положим 7о = {(ж, у) Е dD \ {0} : у = 0}, 7« = {(ж, у) Е 9D \ {0} : arctg ^ = а}. Для угловых областей справедлива следующая теорема. Теорема 2. Пусть ф — обобщенное решение уравнения (1) в круговом секторе D раствора 0 < а <2%, удовлетворяющее граничным условиям lira ^(ж,у)= Ига ^\х,у)=0. (6) (1,у)—7а (х-УНЮ оу Предположим, что для некоторого s > ^ и всех, достаточно малых г > О, выполнено ess sup |V99(k, у) | < exp < —^ Тогда р = О в D.
2. Комплексный потенциал Пусть D — односвязная область. Наряду с потенциальной функцией р(х,у) рассмотрим функцию тока ф(х, у), связанную с р соотношениями: f Фх — ~ору ,g. t Фу = °Тх Из соотношения (3) следует, что для любого замкнутого спрямляемого контура С, обладающего свойством mesi (С А Въ^рУ= О- выполнено У a(g) (-pydx + pxdy^ = 0. с Ясно, что для любой пары точек а, b € В почти все ломаные С С В, соединяющие а и Ь, обладают указанным свойством. Таким образом, для произвольным образом фиксированной точки a G В мы можем положить (х,у) Фкх' У) = У а^ (- а и локально липшицева в В функция ф, удовлетворяющая (8), действительно существует. Комплекснозначная функция Q = р+гф называется комплексным потенциалом. Рассмотрим квадратичную форму ds^ = dtp2 + dф2 = (pxdx + Pydy)2 + <^$dx + фydy)2 = = Vx + °гЧ^ dx2 + 2(1 - a2) pxpy dxdy + (^ + ^^ ^2 = = gi 1 dx2 + 2y12dxdy + g^ dy2. Данная форма положительно определена в каждой точке, где |Vy)| > 0. Обозначим через gy(i,j = 1,2) коэффициенты матрицы (дР), обратной к матрице (Уу). Положим д = det (д^). Мы имеем 9 = 911922 - 912 = О2 |Vy|4 и, далее, в силу соотношений ^11 __ 922 12 = 912 22 _ 911 9’9’ уравнение Лапласа — Бельтрами для гармонических в метрике ds^ функций и^х, у) переписываем в виде д ( „ди _ u ди\ д /^ди\ + + Здесь обозначено И _ ^У + 67 ^Z 12 _ 21 _ (1 — ^фх фу 22 _ Фх + °2 Фу.... У ^[V^4 ’ 9 9 a2|V< ’ 9 ~ ^IV^I4 ' W Система Коши — Римана в метрике ds^ тогда принимает вид ди _ (1 - сг2)^ фу ди _ Ф2 + о-2 у?2 ди дх ди _ Ру + о2 Ф2 ди _ (1 - а^фх Фу 9и ^ ду о jVy>|2дх о IV^j2ду (см., напр., [7, Гл. 1, § 1]). Несложно проверить следующе утверждение. Лемма 1. Функция Q(x, у) голоморфна в метрике ds^ Для доказательства достаточно заметить, что при и = ф и и — ф система (12) обращается в систему (8). Естественным образом определяется понятие простой жордановой дуги в D (открытой или замкнутой) и простой жордановой кривой. В частности, простыми жордановыми дугами в D являются нециклические сечения области D [11, § 3], а множество простых концов D \ D есть простая жорданова кривая в D. Пусть Еу, Е^ — произвольные множества и 7 С D — простая жорданова дуга. Будем говорить, что 7 разделяет множества Еу и Е^ в D, если для любого связного, замкнутого в D множества К такого, что КС\Ег ^ 0 (г = 1,2), выполнено КГ\^ ^ 0. Пусть D' — подобласть области D и е' Е D\D — простой конец. Говорим, что подобласть D' примыкает к простому концу Е, если для любой последовательности {ап} точек области D, сходящейся к е', существует номер N такой, что при всех n > N точки ап принадлежат подобласти D*. Пусть а = (а;0) Уо) € D \ DbQp) — произвольная точка. Всякий бесконечно малый круг в метрике ds^ с центром в точке а G D является бесконечно малым эллипсом с характеристиками (р,6\ При этом, как легко видеть, мы имеем р(жо,т/о) = lM|V^(z0,y0)|) • Предположение (2) означает, что характеристика р локально ограничена в области D. Пользуясь известными результатами (см., напр., [12, теорема 9]), заключаем о существовании квазиконформного отображения f : D —^ R2, характеристики которого почти всюду в D совпадают с (р,0\ Данное отображение вводит изотермические координаты на абстрактной поверхности (D, ds^ и является конформным в метрике этой поверхности. Фиксируем произвольно три простых конца е',е0,е” Е D\D, расположенных в порядке положительного обхода границы D \ D. Пусть I С D — жорданова дуга, отделяющая в D конец е' от е0 и е". Выберем локально липшицеву функцию h : D —» (0,1) со свойствами: lim h(x,y) — 0, h\. = 1, (13) (т,у)—>е' и такую, что для любого компакта А С {(т,д) Е D : 0 < Цх,у) < 1} выполнено essinf |Х7^(х,у)| > 0. (14) А Компоненту связности множества {(х, у) Е D : h(x, у) = i}, отделяющую простой конец в* от е0 и е", обозначим через Е^ . Положим М^ = У (9П^ + 2g12hxhy + g22/72) -^ V^Tdy5, где g^ (i,j = 1,2) — элементы матрицы (gv), определяемые соотношениями (11). Имеет место следующая лемма. Лемма 2. Пусть f : D —> R2 — однолистное, конформное в метрике ds^ отображение. Тогда если f dt <15) о то образом простого конца В является некоторый простой конец области f(D). Доказательство непосредственно вытекает из «принципа длины и площади» в метрике ds^ [13]. Действительно, пользуясь (14), на основании неравенства (10) главы XIV [13] мы можем записать / osc2(/, (у11 l/x|2 + 2д12^ f^ + у22|/у|2) don, (16) о где символом (■, •) обозначено скалярное произведение и Аоп = \jgwg^ - g^dxdy = o\Vp\2dxdy - элемент площади в метрике ds^. Если f(D) = R2, то граница f(D) имеет единственный простой конец, и наше утверждение тривиально. Пусть f(D) ^ R2. Так как простые концы инвариантны при конформных отображениях, то, не умаляя общности, можем считать, что область f(D) есть единичный круг В = В(0,1). При этом предположении находим jjD(gn\fx\2 ^Зу12^,^ + д^^ ^jj ^dxd;g = = 2 area/(D) = 2тг. Здесь с целью упростить вычисления достаточно было заметить, что первый из двойных интегралов является интегралом Дирихле для отображения /, конформного в метрике ds^. В силу (16) имеем / osc2^,E^t))^-r< оо. О Из условия (15) теперь следует, что вдоль некоторой последовательности дуг ^Eh(tk)Y (к оо), выполнено lim osc(/, Е^кУ) = 0. к—>оо Каждая из дуг E^ik) отделяет простой конец е' от дуги еое'. Однако lira diam/(Dh(ifc)) = О, к—>оо и для произвольной последовательности точек ат Е D, ат —» е' мы вправе утверждать, что V(am^ сходится к некоторой точке на границе ЭВ.
4. Отображение на полосу Пусть В — односвязная область, отличная от R2, и пусть ^ — обобщенное решение уравнения (1). Рассмотрим произвольное семейство замкнутых, локально спрямляемых дуг 7 6 Г, лежащих в области В, и таких, что mesi (7 П Вь^рУ) = 0. Измеримая по Лебегу, локально ограниченная, неотрицательная функция р(х,уУ определенная в области В, называется допустимой для семейства Г в метрике ds^, если для любой дуги 7 € Г выполнено j p(x,y)dsn>l. (17) Величина modnr = inf j p2(x,y)dan, (18) D где точная нижняя грань берется по всем допустимым для Г в метрике ds^ функциям Р^с^уУ называется модулем семейства Г в метрике ds^. Некоторые примеры вычислений и оценок модуля семейства кривых в римановой метрике можно найти в [10]. Фиксируем три простых конца е', е0 и е" на границе области В, расположенных в порядке положительного обхода В\ В. Предположим, что в окрестности простого конца е* метрика ds^ обладает описанным выше свойством (15). Предположим дополнительно, что 0 < ess inf tr(|VWz, у) I) < esssupo"(|V^(a:, y)l) < сю (19) А А для всякого компакта А С В \ {е'}. Ясно, что условие (19) влечет выполнение (15) в каждом простом конце eeD\{e'}. Пусть / : В —> R2 — однолистное, конформное (в метрике ds^ отображение со свойствами: ЛЧ = П, n={(»,»)etf:^<»<|}, и lira ц(ж,у) = +оо, /(е0) = (0,1), lira и(х, у) = -оо. (20) (т,у)-»е" Фиксируем локально липшицеву функцию h : В —> [0,1], для которой lim h(x, у) = 0, lim_Ых^ = 1. (21) (^^-^е* (z^—teoc" Предположим, что h обладает также свойством (14). Для произвольной дуги Eh(f), 0 < t< 1, символом 8(f) обозначим семейство всевозможных локально спрямляемых дуг 7, mesi (7 Г) В^УрУ) = 0, таких, что [7)5 —"— ——— 60 В.М. Миклюков, С.С. Полупанов, Р.А. Тарапата. К задаче о стабилизации разделяет в D конец е! и дугу еое" так, что [7)5 П [^(i)]^ / 0. Пусть, A (t) — семейство дуг, разделяющих Eh(t) и еое" в D. Следующее утверждение представляет собой одну из возможных (модульных) версий хорошо известных теорем Альфорса — Варшавского о конформных отображениях полос [И], [15]. Лемма 3. В описанных предположениях для всякого однолистного и конформного в метрике ds^ отображения / с нормировкой (20) выполнено и(ж, у) < к (modfi A(t) + modg f (t)) для всех (ж, у) е Eh(t) (22) и osc (и(х, у), E^t)) < 27rmodn£(£). Доказательство ограничивается ссылкой на теорему 3.1 из [16]. Эта теорема доказана в [16] для отображений области на полосу, конформных в евклидовой метрике. Заметим, однако, что при отображениях, конформных в римановой метрике, модуль семейства кривых в этой метрике преобразуется в модуль семейства их образов в соответствующей метрике. Поэтому все рассуждения из [16] проходят без каких-либо существенных изменений также и в нашем случае для отображений поверхности (D, ds^ на полосу П, конформных в римановой метрике.
5. Подготовительная теорема Нам потребуется некоторая версия известной теоремы Фрагмена — Линделефа: Лемма 4. Пусть F : П —» R2 — голоморфна в П и удовлетворяет неравенству где v^) — положительная непрерывная неубывающая функция. Если +оо v(u) e-4du = +ос, (25) то F(u, у) = 0. Доказательство в предположении непрерывности F вплоть до границы можно найти, например, в [8, теорема 6.3 главы VIII]. В общем случае доказательство практически не меняется — достаточно рассмотреть F в более узкой полосе {(u, и) 6 R2 : |и| < с < ^}, с = const, и перейти к пределу. Следующая теорема типа Фрагмена — Линделефа для голоморфных в метрике ds^ функций носит подготовительный характер. Вестник ВолГУ. Серия L Вып. 9. 2005 61 ..........— Теорема 3. Пусть D С R2 — односвязная область, отличная от R2. Пусть е', е0и в" — простые концы на dD и h : D —► R — локально липшицева функция, подчиненная условиям (21) и (14). Предположим, что решение р уравнения (1) удовлетворяет условиям (19), (15). Пусть Ф : D —> R2 — функция, голоморфная в метрике ds^ и такая, что In |Ф(ж,у)| <—i/(t) для всех (х,у) е Eh(t) (0 < t < 1)(26) для некоторой положительной непрерывной неубывающей функции и. Пусть т = 0(t) — строго монотонно убывающая, непрерывная на (0,1) функция, ^(+0) = +оо и -к (modn A(t) + modp 8(t)) < 0(1) (0 < t < 1).(27) Тогда если +оо j и ((^(т)) е~Т dr = -Too,(28) то Ф(ж, у) = 0. Доказательство. Обозначим через / однолистное, конформное в метрике ds^ отображение, приводящее квадратичную форму ds^ к виду А(и, и) (du2 + dv2). В силу предположений (15), (19), мы можем считать, что f(D) = П и удовлетворяет условиям нормировки (20). Положим Р(и,и) = Ф о /-1 (u, v). Данная функция голоморфна в полосе П в евклидовой метрике. Из условия (26) следует, что sup |Ф(ж,у)| < Dt где Dt = {(ж, у) € D : h(x, у) < t). Таким образом, sup |Ф о У-1 (u, v)| < е-1^. Однако, в силу (22) и (27), выполнено и < 0(1) для всех (и, и) € D \ f(Dt). Функция v(t) не убывает, а потому при всех (т, и) 6 П имеем ^oy-1^), ^е^М и, далее, ln|F(r,u)| < -щ(т), где ^(т) = v (0-1(т)). Условие (28) влечет +оо j щ(т)е-т = оо. По лемме 4 заключаем, что F(u, v) = 0. Тем самым, Ф(т,у) = 0 и теорема доказана. В.М. Миклюков, С.С. Полупанов, Р.А. Тарапапга. К задаче о стабилизации
6. Две леммы Фиксируем t, 0 < t < 1, и подобласть Dt, определенную в предыдущем разделе. Оценим modpA(i). Рассмотрим семейство Л*(<) всевозможных локально спрямляемых дуг 7, лежащих в D \ Dt, удовлетворяющих условию mes (7 Г\ Вь(^ = О и соединяющих в D\Dt граничную дугу еое" с Eh(tY В соответствии со следствием 2.1 из [9], мы имеем modpA(f) = —--1 (29) modpA (f) В монографии [9] данное свойство доказано для модуля семейства кривых в евклидовой метрике. Однако, если в теореме 2.3 [9] вместо отображений, конформных в евклидовой метрике, использовать конформные отображения в метрике ds^, то доказательство (29) остается неизменным. Далее мы воспользуемся известной связью между модулем и емкостью конденсатора [10, лемма 1.1]. Мы имеем modpA*(t) = сарр (^Ек(Д eQe"; D\Dt^ , (30) где сарр(£\(£), еое"; D\Dt) = inf // (g11^ + 2g12^^ + do^ J J D\Dt и точная нижняя грань берется по всем локально липшицевым функциям £ : D \ Dt —> R, для которых еое" — 1’ ^ lEh(0 — $ • Легко видеть, что /[ (у11^ + 2д12£Л + У22^) М = J J D\Dt Py 4- C2^2 1 — CT2r (^2 + C72 2 »|Vy|2 & 2<7|V¥>|2*’'^i&+<7|VV|2^)dldv- D\Dt Py^x ^РхРу^х^у + Vx^y Px^X 4" ^PlPy^X^y 4" Py^>y cr|V |v dxdy = i L/v^y+i/v^y > dxdy, D\Dt I \ IWI/ О \ |V МАТЕМАТИКА Замечая теперь, что а( V£ / 1 min cr, — \ cr \ ^IV^I/ + V’ |v 2^ = min ( or, — ) |V£|2, мы получаем D\Dt I min [ст,—j \V^\2dxdy. D\Dt \ a) Учитывая (29) и (30), приходим к следующему утверждению. Лемма 5. Имеет место оценка Укажем другую полезную оценку для модуля семейства дуг в метрике ds^. Для произвольного семейства Г локально спрямляемых дуг 7 мы имеем modnr = infp>o j^ р\х, у) inf = infp>0 -^IZ inf-, ■7, где р = p|V«p| и _ "" IVvl2 dl 2) ^^ dxdy + ^ t ^2^^2 IV92I2 У |V 2 y‘ Легко видеть, что > min(l, u2)(dx2 + dy2Y Поэтому, полагая Ркх^ = Р^у^ min(l,ст) и замечая, что приходим к соотношению Таким образом, доказана следующая лемма. Лемма 6. В описанных предположениях справедлива оценка modoF < inf /9>0
7. Угол Рассмотрим круговой сектор раствора а, 0 < а < 2тг. Фиксируем простые концы е'= (0,0), во = (1,0), е" = (cos а, sin а) и функцию Цх^ у) = дД2+ у2. Легко проверяется, что h удовлетворяет (14) и (21). Далее для произвольного 0 < г < 1 полагаем SD(0, г') = ПГ! {(ж, у) : х2 + у2 = г2}, BiD(0, r) = DQ{(x, у) : х2 + у2< г2}. Воспользуемся леммой 6. В силу (32) имеем Полагая здесь By(t) = BD(0,2t) \ BD^, t/2) и получаем 1 ^(ж,у) О при (х,у)ЕВОД, вне Вр(^, modn£i(i) < Поскольку для произвольной дуги 7 Е £i(£) выполнено j h \х, у) Vdx2 + dy2 > а, TG^l(t) приходим к оценке modnfi(i) < Л max (а, 1/а) h2(x,y) Чтобы оценить modnf2(t), заметим сначала, что всякая дуга 7 Е £2(t) пересекает одновременно 8О(ОД и хотя бы одну из дуг SD(0,t/2\ SD(0,2t). Отсюда заключаем, что modnf2(£) < modn£3(t) + modn£i(£), (35) где £3^ = {7 G ОД : 7 П SD(0, t/2) ^ 0}, 84^ = {7 € 8(i) : 7 П Sp(0,2^ ^ 0}. На каждой дуге 7 G £3(t) выберем поддугу 7*, лежащую в области D П {f/2 < /г(ж,у) < £} и соединяющую Sd(0, V2) с Вд(0,£). Пусть 83(f) — семейство всевозможных таких дуг 7*. Легко видеть, что modn£3(£) < mod^*^). Выбирая теперь в (32) плотность р(х,у) = 1/Цх,у) при (ж, у) е BB(t), где Вд (t) = Вд(ОВ) \ Bp(0,t/2), и доопределяя ее нулем во всех остальных точках, мы находим // шах (и, 1/сг) h~2(x, у) dxdy ™аа£;т < Взй>^ < inf / /г-1 (ж, у) 7 v 7*e^(t), < Ь-2 2 И max (а, 1/сг). h2(x,y) Тем самым, modnB3(i) < In"2 2 max (er, 1/cr) v(36) JJb^w h2(x,y) Аналогично, modn£4(f) < In"2 2 max(tr, l/cr) .(37) Ws“(2<) h?(x,y) Объединяя теперь (33)-(37), приходим к утверждению. Лемма 7. Если 0 < 2i < 1, то modn^(t) < (-^- + max fa, 2^2'< \1п22 JJBbW V °"У х2 + у2 Оценим modnA(t). Здесь мы будем пользоваться леммой 5. Введем обозначение = inf min (а, 1/<т). D\BD(0,t) Мы имеем inf И min (g, — ) |V^|2da;d?/ >//*(t)inf |V^|2da;dy = JJd\bd(o^ \ a / ^ J JO\BD(0,t) = p*(t) cap(SD(0, i), eoe"; D \ BD(0,<)), где символом сар(А, В;С) обозначена обычная конформная емкость конденсатора (А, В; С) (см., напр., [17, § 3, гл. II]). Так как область D есть угол раствора а > 0, то cap(BD(O,t),eoe";B\BD(O,t)) = 7-777. In 1/t Тем самым приходим к оценке inf// min \V^\2dxdy > (39) JJd\Bd^A \ ° / In 1/t Имеет место следующая теорема. Теорема 4. Пусть D — круговой сектор раствора 0 < а<2% с вершиной в начале координат. Пусть у) — обобщенное решение (1), удовлетворяющее условию (19), и такое, что Г dt / / (ст + ст-1) л/da? + dy2 = +00.(40) о ' So(0,c) Пусть Ф : В -^ R2 — функция, голоморфная в метрике ds^, причем In |Ф(ж,g)| < —z/(t) для всех (х,у) G ^(О, t) (0 < t < 1)(41) для некоторой положительной непрерывной неубывающей функции и. Пусть т = 0(t) — строго монотонно убывающая, непрерывная на (0,1) функция, 0(+О) = +оо и ^^TS + i<«№ (0 где (2 1 \/ 1 \ —5—I—- и p*(t) = sup max (ст, — . In 2 a2) B..^ \ a J Тогда если v удовлетворяет (28), то Ф(х,у) = 0. Для доказательства воспользуемся теоремой 3. Так как |Vh| = 1, то мы можем положить Vh(x,y) = (cos Р, sin PY В силу (И) имеем A^(t) = j (g11 cos2Р + 2g12 cos Р sin Р + g22 sin2P^ y/g Vdx2 + dy2< < j (cr + cr x^dx2 + dy2 Sd^A и условие (15) выполнено, если выполнено (40). Заметим теперь, что при 0 < 2£ < 1 из (38) следует ( 2 1 \ modn5(t) < 2а In 2 —2—Н — ) //*(£). \ In 2 а2 7 Кроме того, объединяя оценки (31) и (39), находим . . . . In 1 /1 modnA(£) <---—. Q/l*^) Таким образом, modnA(t) + modQ^(t) < + a In 2 f 4) м'и ацДч \ln 2 и условие (42) влечет (27).
8. Доказательство теоремы 2 Выберем постоянную к > 1 так, чтобы л к— < з. а По лемме 1 комплексный потенциал Q является голоморфной в области D функцией. На основании (6) легко убеждаемся, что решение 99 = 0 на 70, а сопряженная функция ^, определяемая равенством (9), является тождественной постоянной на 7q. Обозначим через С эту постоянную и рассмотрим голоморфную функцию Г2г = О — г С. При всяком 0 < г < 1, пользуясь (7), имеем supsD(0,r) |Qi| < osc(^,SD(0,r)) + osc(^-C,5D(0,r)) < < j |Vi/)| V^2 + dy2 + j ^^Vdx^^dy2< SD(O,r) SD(O,r) < ar exp + ar exp sup cr(|V<^|). r J SD(0,r) Условие (7) влечет, что Vip(i,y) —> 0 при (ж, у) —> 0. Так как коэффициент a(q) в (1) является непрерывной функцией и a(0) — 1, то мы можем считать, что при достаточно малых t > 0 величины sup cr(|V SD(0,i) и Р-Ч^ не превосходят к. Поэтому при достаточно малых t > 0 выполнено sup |Qi| < 2aiA:exp 8В(РА где si — некоторая постоянная, к-а < Si < s. Воспользуемся теоремой 4. Предположение (40) следует из ограниченности а + ст-1 в окрестности точки 0. Условие (41) вытекает из (7) с функцией z/(t) = —■ к ’ ts' Далее находим lnl/t , In 1/t _ , тг----у-г А-Сур, (<) < тг к--h Ci к = 0(t\ ap,^t) а Замечая теперь, что для обратной функции ., . f а т — Ci к t — 6 (T)=expJ ---- I тг к справедливо убеждаемся в (28). Наше утверждение следует теперь из теоремы 4.
9. Полуполоса Здесь рассуждения близки к предыдущим, поэтому ограничимся лишь узловыми моментами. Рассмотрим полуполосу П = {(ж,?/) : 0 < х< оо, 0 < у< /г}. Зафиксируем простые концы е" = (0,0), во = (0,1), е' = оо и функцию 1 + х Легко видеть, что данная функция удовлетворяет условиям (14) и (21). Для произвольного 0 < t< +оо обозначаем Sn(t) = П А {(ж, у) : h,^ = t}, Bn(t) = П А {(ж, т/) : /г(ж) < t}. Оценим modn£(Z). Фиксируем постоянные Д > 0 и t > 0 так, чтобы 0 < Д < t. Обозначим через £i(£) множество всевозможных дуг 7 Е £(£), расположенных в Bn(t + Д) \ Bn(t - Д), через 82(t) — множество дуг у Е 8(8) \ 8i(t\ Мы имеем modnf (i) < modn^i^) + modn^fi). Полагая здесь QnW = Bn(t + Д) \ Bn(t - Д) и Р^,У) = 0 при ($,y)eQ^(t), вне Qn(8), как и выше, в разделе 7, получаем modn£i(t) < Поскольку для произвольной дуги 7 Е 8i(t) выполнено j Vdx2 + dy2 > h, Te^dt) приходим к оценке modo^i(t) < max ((7,1/(7) dxdy. Чтобы оценить modg^2(^), заметим теперь, что всякая дуга 7 € 82(8) пересекает одновременно Sn(t) и хотя бы одну из дуг Sn(t — Д), бп^ + Д)- Отсюда заключаем, что modn^2(^) < modQ^3(^) + modnf4(t), где 8з^ = {7 € ^(t) : 7 П Sn(i - Д) ^ 0}, ^4(t) = {? e E^ : 7 П Sn(t + Д) ^ 0}. На всякой дуге 7 £ ^з(^) можно выбрать поддугу 7*, лежащую в области П П {^ — Д < Цх^у') < ^ и соединяющую Sxv(t — Д) с 8^(8). Пусть 8^8) — семейство всевозможных таких дуг 7*. Легко видеть, что modfif3(t) < modfiS^t). Выберем в (32) плотность р(ж, у) = 1 при (ж, у) Е Qn(tYгДеQn^ = = Bn^XBn^t — А), и доопределим ее нулем во всех остальных точках. Мы находим // max (сг, 1/сг) dxdy modfi£3-(t) <У«2»1_< inf j >/dx2 + dy2 \ 7*6f3*(t); < A~2 /1 max (cr, 1/cr) dxdy. Тем самым, modQ JjQKW Аналогично, mod^f^f) < A-2 // max (cr, 1/cr) dxdy.(47) Объединяя теперь (43)-(47), приходим к утверждению. Лемма 8. Если 0 < 2t< 1, то /2 1 \ Г Г/ 1\ modn5(0 < — + / max ( cr, - dxdy.(48) VA П ) а^шV ^7 Оценим modnA(Z). Здесь, как и ранее, мы пользуемся леммой 5. Введем обозначение 5,(0 = inf min (a, 1/cr). п\вп(г) Имеем inf Ц min (сг, — ) |V£|2dxdy >5,(0 inf |V£|2dxdy— J7n\Bn(t) \ °) ^ JJn\BnW = 5,(t) cap(Sn(t), вое"; П \ Bn(t)y Поскольку область П есть полуполоса ширины h > 0 и область П \ Вп(0 является прямоугольником длины (1 — t^/t, то cap(6'n(t), еое"; П \ Bn(t)) = Отсюда приходим к оценке inf / / mm I <7, — I V^ \ dxdy > —-----. (49) ^ J Jn\BnW \ a/ 1 - Теорема 5. Пусть П — полуполоса ширины 0 < /г < +оо. Пусть <р — обобщенное решение (1), удовлетворяющее условию (19) и такое, что Jt4dt / J о ' Sn(t) Пусть Ф : П —>R2 — функция, голоморфная в метрике ds^, причем 1п|Ф(ж,?/)| < -u(t) для всех (х,у) Е Sn(t) (0 < t < 1)(51) для некоторой положительной непрерывной неубывающей функции и. Пусть т = 9(f) — строго монотонно убывающая, непрерывная на (0,1) функция, 0(+О) = +ос и (О < t < 1),(52) где / 21 \ С2 = ivhA — + — ) и 8*(f) = sup max I <7, — I . \Д2 Q^t) V о J Тогда если v удовлетворяет (28), то Ф(т,у) = О. Доказательство. Мы пользуемся теоремой 3. Имеем Vh — (1/(1 + т)2,0). В силу (Н) XhW = (i^ j 9й Vd Vd^^V < SnU) - 0+*)4J а |Vy|2 1^1 Snd) и (15) выполняется, если выполняется (50). Из (48) вытекает, что modn£(t) < 2/г.Д 5*^)- Объединяя оценки (31) и (49), получаем modnA(t) - isib Тем самым, 1 — t / 2 1 \ modnA(t) + modn^(t) < "^щ^ + 2^А д^ + ^2 у и на основании (52) заключаем о справедливости (27).
10. Доказательство теоремы 1 Выберем постоянную к > 1 так, чтобы , 7Г к— < S. п Согласно лемме 1 комплексный потенциал Q голоморфен в П. В силу (4) убеждаемся, что у? = О при у = h, а ^ = С, С = const, при у = 0. Положим Qx = Q — г С. При всяком 0 < t < 1 на основании (5) имеем suPsn(t) lQil ^ М*)) + osc(^ - С, Sn(t)) < |V<^||dy|+ j |V^||t/y|< Sn(t) SnW < /г exp {— exp{st}} + /гехр{— exp{si}} sup Sn(t) Из (5) вытекает, что Vip(x,y) —> 0 при х —► +оо. Поскольку коэффициент a(q) в (1) непрерывен и ст(О) = 1, то при достаточно малых t > О величины sup Sn(t) МС не превосходят к. Тем самым, при малых t > О получаем sup |Qi| < 2hk ехр{—exp{st}} . Sn(t) Воспользуемся теоремой 5. Выполнение (50) при х = +оо очевидно. Требование (51) следует из (5) с функцией v(t^ = exp — exp s(l - t) 1t J Далее находим + ^ 8*W - + C2k = 9(t\ Заметим теперь, что для обратной функции t = e-\T^ 1 + ^ (т - ОД Tvk выполнено (28). Необходимое утверждение вытекает из теоремы 5.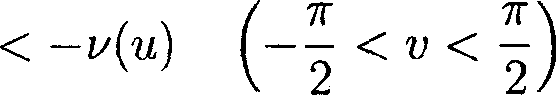
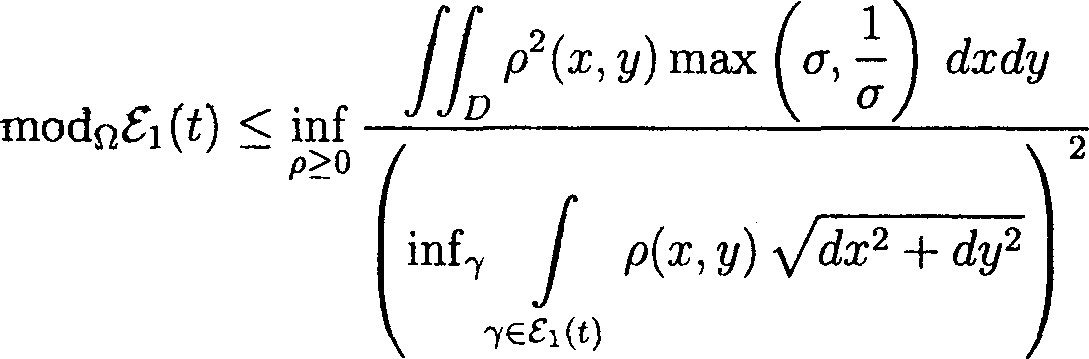
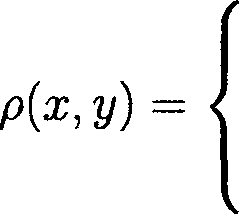
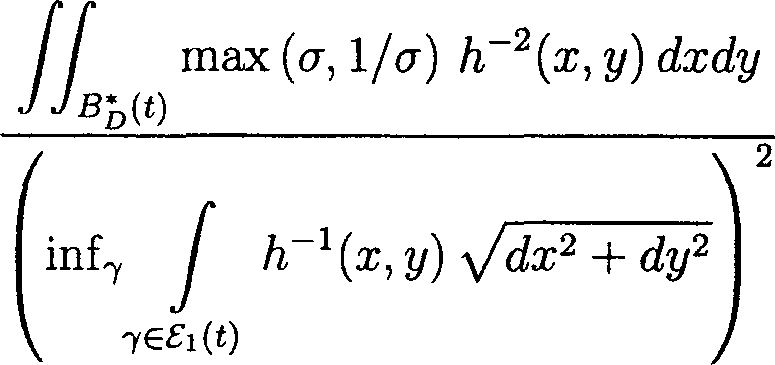
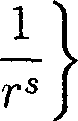
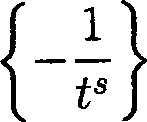
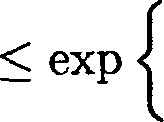
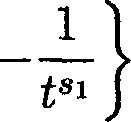
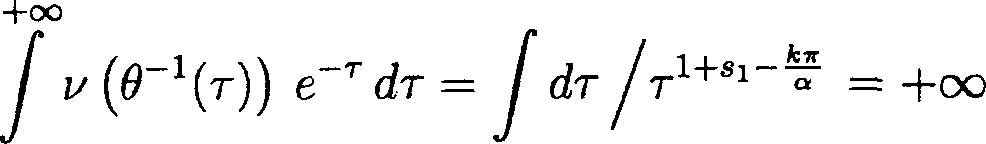
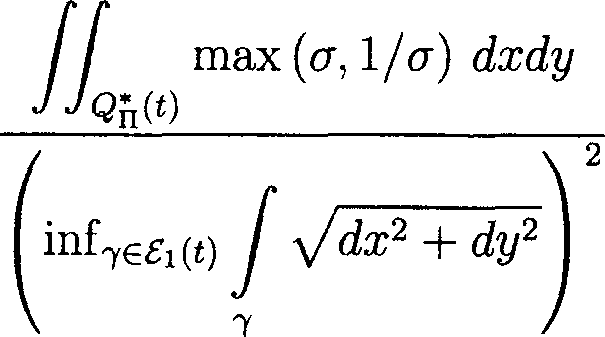
Список литературы К задаче о стабилизации решений уравнения газовой динамики
- Лаврентьев М.А., Шабат Б.В. Проблемы гидродинамики и их математические модели. М.: Наука, 1973.
- Alessandrini G. and Nesi V. Univalent σ-harmonic mappings//Arch. Ration. Mech. and Anal. 2001. V. 158. P. 155-171.
- Faraco D. Beltrami operators and microstructure. Academic dissertation. Depart, of Math. Faculty of Sci. University of Helsinki. Helsinki, 2002.
- Федерер Г. Геометрическая теория меры. М: Наука. 1987.
- Миклюков В.М. Зоны стагнации решений уравнения Лапласа -Бельтрами в длинных полосах//Математические труды. 2002. Т. 5. № 1. С. 84-101.
- Миклюков В.М., Полупанов С.С., Тарапата Р.А. О стабилизации решений уравнения газовой динамики//Докл. РАН (в печати).
- Шиффер М., Спенсер Д.К. Функционалы на конечных римановых поверхностях. М.: ИЛ, 1957.
- Евграфов М.А. Аналитические функции. М.: Наука, 1968.
- Дженкинс Дж. Однолистные функции и конформные отображения. М.: ИЛ, 1962.
- Миклюков В.М. Некоторые признаки параболичности и гиперболичности граничных множеств поверхностей//Изв. РАН. Сер. матем. 1996. Т. 60. № 4. С. 111-158.
- Суворов Г.Д. Семейства плоских топологических отображений. Новосибирск: Изд-во СО АН СССР, 1965.
- Белинский П.П. Общие свойства квазиконформных отображений. Новосибирск: Наука. Сиб. отд-ние, 1974.
- Суворов Г.Д. Обобщенный «принцип длины и площади» в теории отображений. Киев: Наукова Думка, 1985.
- Ahlfors L.V. Untersuchungen zur Theorie der konformen Abbildung und der ganzen Funktionen.//Acta Soc. Sci. Fenn. 1930. V. 1. № 9. P. 1-40.
- Warschawski S.E. On conformal mapping of infinite strips//Trans. Amer. Math. Soc. 1942. V. 51. P. 280-335.
- Миклюков В.М. О некоторых граничных задачах теории конформных отображений//Сиб. мат. журн. 1977. Т. XVIII. № 5. С. 1111-1124.
- Решетняк Ю.Г. Пространственные отображения с ограниченным искажением. Новосибирск: Наука, 1982.


