К задаче оптимизации расположения сферических треугольников

ВЕСТНИК Мордовского университета | Том 25 | № 1 | 2015

area of a spherical triangle.

При конструировании сборных сферических оболочек возникает задача оптимального расположения треугольной сети на сфере с целью минимальности числа типоразмеров. В работах [3–4] были предложены некоторые варианты решения этой задачи.

В данной работе приводятся математическая постановка задачи оптимизации и способы ее решения.

Пусть имеется произвольный сферический треугольник АВС , внутренние углы которого равны соответственно А, В и С . Как известно [1–2], всякий такой треугольник определяется по каким-либо трем заданным параметрам.

Постановка задачи. В треугольник АВС требуется вписать равносторонний сферический треугольник наименьшей площади.

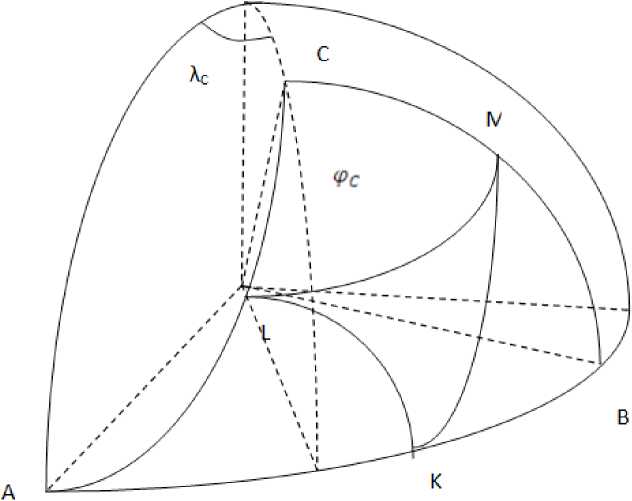
Для решения поставленной задачи воспользуемся результатами аналитической геометрии на сфере [1]. Подобно прямоугольным координатам на плоскости, введем координаты на сфере. Возьмем точку А данного треугольника и назовем ее началом системы координат. Две взаимно перпендикулярные окружности больших кругов, проходящих через точку А , будут являться координатными осями. Таким образом, произвольная точка на сфере будет однозначно определена

двумя координатами – широтой φ и дол- динат можно назвать полярной системой готой λ (рисунок). Данную систему коор- сферических координат.

Серия « Естественные и технические науки »

и с у н о к

Составив уравнения сторон треугольника АВС по формуле (1), получим следующее:

AB - tg ϕ = 0 ⇒ ϕ = 0, 0 ≤ λ ≤ λ _B ,

Р

Прямой на сфере будем называть любую окружность большого радиуса. Тогда уравнение прямой, проходящей через точки M 1{ ф 1 , Я ₂) и M ₂ ( ф ₂ , Я ₂) , имеет вид:

tgϕ=

tg ϕ ₁ sin( λ - λ ₂) - tg ϕ ₂ sin( λ - λ ₁)

sin( λ ₁ - λ ₂)

, (1)

AC - tg ϕ = ^{tg ϕ C} sin λ , 0 ≤ λ ≤ λ , sin λ _C               ^C

а расстояние s между этими точками, которое называется сферическим, определяется из соотношения:

cos 5 = sin ф 1 sin ф+ +

+ cos ф _г cos ф ₂ cos( Х 1 - Х ₂ ).    (2)

Таким образом, данный сферический треугольник в выбранной системе координат определяется точками.

A (0,0), B (0, Я в ), C ( ф с , Я с ),

о<фс <2,0<Яс <Яв <2.

BC — tg Ф =    tgФс . х sin (^ — ^Е ) , sin ( ^с ^Е )

1. < я < ^.

CB

Предположим, что MNK – искомый вписанный равносторонний треугольник. Обозначим внутренний угол этого треугольника D , длину стороны – s. С учетом системы координат, получаем: K ( 0, Л к ) , L (фк , Л к ) , M ( ф м , Л к, ) . Тогда из (2) определим сферическое расстояние между этими точками:

LK - cos s = cos ф _L cos ( X _K - X L ) ,

MK - cos s = cos ф _м cos ( X, - X ),

MMK

LM - cos s = sin ф _L sin ф _м +

+ cos ф _L cos ф _м cos ( X _M - X L ) .

Для того чтобы всякий треугольник, вписанный в треугольник АВС , был равносторонним, необходимо выполнение ряда условий:

cos ф _L cos ( X K - X L ) =

Пусть S _KLM – площадь треугольника KLM, тогда

SKI MD ³ D ^П (для сферы радиуса R=1).

Из этого очевидно, что площадь будет наименьшей при наименьшем угле D .

Таким образом, поставленная задача свелась к задаче минимизации угла сфе- рического равностороннего треугольника, как функции введенных координат D = D (фм,XK, XM ), удовлетворяющие условиям (3).

Задача условной минимизации: Найти наименьшее значение функ-

= cos ф м cos ( ^X m — X ) , cos ф _L cos ( X K - X L ) = sin ф _L sin ф _м +

ции:

D = arccos

cos Фм cos ( Xm - Xk )

+ cos ф _L cos ф _M cos ( X M - X L ) .

1 + cos фм cos ( Xm - Xk )

удовлетворяющей системе условий:

При этом

L ∈ AC ⇒ tg ϕ = ^{g ϕ C} sin λ , ^L   sin λ _C      ^L

0 ≤ λ L ≤ λ B ,

K ^ AB ^ ф _к = 0, X =

= X ,0 ² X ² X ,

KKB

' 0 <  T l ^ Ф е ,0 ^ Ф м ^ Ф е ,

0 <  X ^ X ,0 ^ X ^ \- ,

KB LC

^X C <  ^X M <  ^X b ^,cos T l ^cos ( ^X K - ^X ) =

= cos Ф м cos ( ^X M - ^X K ) ,cos T l ^cos ( ^X K ^{- X} L ) = ^sin T l ^sin Ф м +

+ cos T_l cos Ф _м cos ( X M - X L ) .

ВЕСТНИК Мордовского университета | Том 25 | № 1 | 2015

M e BC ^ tg ^ M =

=     Y''     sin ( X M - X , ) .

sin ⁽ X ^A b )

Определяя взаимосвязь внутреннего угла со сферическим расстоянием равностороннего треугольника, получаем соотношение:

2 s

1 - tg у cos D =------2, из которого определяется связь с введенными координатами:

cos D = ^cos Ф м ^cos ( ^ M - ^ K )

• ^{1    + cos} Ф м ^cos ( ^ M ^- ^ K )

По условию задачи, треугольник KLM – сферический равносторонний треугольник, поэтому угол D удовлетворяет условию:

n < 3D < Зп .(4)

Отсюда приходим к условию:

n

• -3-    < D < n .

Тогда, если ввести обозначение z = cos фм cos (Xm - Xk ),(6)

то функция

D = arccos

z

1 + z

удовлетворяет (4), если

• - 2 <  z <  1 .            (7)

Следует отметить, что в области (5) выполняется условие

D = — ,--- ¹ ----< 0,

• V1 + 2 z (1 + z)

следовательно, наименьшее значение функции D = D ( ф _м , X K , X M ) в области (5) может принимать при наибольшем значении величины z.

Таким образом, исходная задача оптимизации принимает следующий вид:

max z , U

- < z < 1

Введя обозначения tg^c 71 + tg2 ^C tgXc

q =

tg ^ c У1 ⁺ tg² X c tg X - ta X,

, k = tg ^X B ,

и проведя замену переменных x = tg^L , y = tg^M получим соотношения:

px tg Vl = I----г ,tg Фм

• V1 + x x

  q ( k ^- y )

  У¹+ yy

  
  

При этом функцию z можно представить в следующем виде:

1 + tg X K x

У 1 + (1 + p ²⁾ x ² У¹ + tg² x _K

Тогда условия равенства сторон KL, LM и KM треугольника KLM примут вид:

<

tg^ K =

У 1 + ( 1 + p ² ) x ² - J 1 + y ² + q ²( k - y )² x J 1 + y ² + q ²( k - y )² - y 1 + ( 1 + p 2 ) x²

1 + tg X K x     pxy +        1 + xy

¹ + tg² XK   у/ ¹ + y ^{2     1} + y ² + q ²⁽ k ^- y ⁾²

Таким образом, исходная задача свелась к поиску максимума функции (9), удовлетворяющей условию (10) в области

0 ≤ x ≤ tg λ _C ,tg λ _C ≤ y ≤ tg λ _B .

Следует отметить, что система (9) определяет неявную функцию y = y ( x ) или x = x ( y ) . Тогда tg A ^ также будет функцией одной переменной x или y В результате полученная задача условной оптимизации может быть сведена к нахождению максимального значения функции z=z ( y ) в области (11).

Случай произвольного остроугольного равнобедренного сферического треугольника

Предположим, что треугольник ABC – равнобедренный остроугольный треугольник. Тогда соотношения (8) принимают вид:

Серия « Естественные и технические науки »

tg^c У1 + tg Xc p =----ГХ------, tgXc q = , p,     , k = tg2 Xc.

У1 + tg 2 2 X c

Возможны два случая:

– точка К расположена на биссектрисе угла С ;

– точка К расположена не на биссек трисе угла С.

Вначале pассмотрим 1-й случай.

Тогда tg X B = tg2 X _C ,tg X _K = tg X C и система (10) принимает вид:

" 1 + tg X c x    =       ¹ + tg X c y

J 1 + ( 1 + p ² ) x ² У¹ + y 2 + q ²⁽ k ^- y ) 2

'                                           .    (12)

1 + tg X c X   ( 1 ^- pq ) xy ^- kpqx + 1

_ У ^{1 + tg} 2 X c     1 + y ² + q ²⁽ k - y ⁾²

Функция Z при этом может быть представлена в виде z =

1 + tg A C x

^{1 +} ( 1 ⁺ p ² ) x²

Таким образом, следует найти максимум функции (13) при выполнении условий (12).

Следует отметить, что без учета условий (12) функция (13) принимает максимальное значение при x = pg-CT e(0,tg2c).

1 + p

Второй случай.

Если ввести обозначение

^Q 1 = "^ ^{1 +} ( 1 ⁺ p ² ) x ² , ^Q 2 = V ^{1 +} y ^{2 +} q ^{2( k} — y ^{) 2} , то тогда оптимизируемую функцию z можно представить в виде

( 1 - pq ) xy + pqkx + 1 ^z —                        ,

^Q 1 ^Q 2

а условия (12) можно записать как z f, • df dz = df dz

5x dy   dy dx ’ где f =____________y-x____________

( x ² + 1 ) Q^ - 2 ( xy + 1 ) Q i Q 2 + ( y ² + 1) Q 1

Применяя приведенные выше результаты к равнобедренному треугольнику с параметрами

7       15

p= 2,q= ,k = (ребра треуголь ника -30, угол С=60), имеем следующие результаты:

– для первого случая – равносторонний сферический треугольник со стороной 15,2036;

– для второго случая – треугольник со стороной 15,2033.

Таким образом, условию поставленной задачи удовлетворяет второй случай.

В результате проведенных исследований поставленная задача условной оптимизации функции нескольких переменных была сведена к исследованию функции одной переменной. Полученное решение позволит проводить более точные расчеты в задачах оптимизации при конструировании сборных сферических оболочек.

ВЕСТНИК Мордовского университета | Том 25 | № 1 | 2015