К задаче устойчивости сдвиговых течений относительно длинноволновых возмущений
Автор: Ревина Светлана Васильевна
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 4 т.18, 2016 года.
Бесплатный доступ
Для отыскания вторичных течений, ответвляющихся от основного стационарного течения при уменьшении вязкости, необходимо рассмотреть линейную спектральную и линейную сопряженную задачи. В работе построена длинноволновая асимптотика линейной сопряженной задачи в двумерном случае при условии периодичности по пространственным переменным, когда один из пространственных периодов стремится к бесконечности. Выведены реккурентные формулы для нахождения k-го члена длинноволновой асимптотики скорости и давления. Показано, что если отклонение скорости от ее среднего по периоду значения является нечетной функцией, то коэффициенты разложения скорости являются четными при четных степенях и нечетными при нечетных степенях волнового числа. Получены соотношения между коэффициентами асимптотических разложений линейной спектральной и линейной сопряженной задач.
Устойчивость течений вязкой жидкости, длинноволновая асимптотика, линейная сопряженная задача
Короткий адрес: https://sciup.org/14318555
IDR: 14318555 | УДК: 532.516
Текст научной статьи К задаче устойчивости сдвиговых течений относительно длинноволновых возмущений
Рассматривается двумерное x = (x1,x2) Е R2 движение вязкой несжимаемой жидкости под действием поля внешних сил F ( x ,t), периодического по пространственным переменным x1, x2 с пери одами '1 = 2п и '2 = 2п/а соответственно, в предположении. что волновое число а ^ 0. Неизвестные поле скорости v ( x ,t) и дав .теине p( x ,t) удовлетворяют системе уравнений Навье — Стокса:
dv ,
— + (v, V)v — vAv = —Vp + F(x,t), div v = 0, где v — безразмерная вязкость. Через hfi будем обозпачать среднее по xi. а нерез hf ii — среднее по прямоугольнику периодов П = [0,'1] х [0,'2]:
'1
hf i = 'Г / f ( x ,t) d xi , hhf ii(t) = |П| / f ( x ,t) d xi d X2 •
Ω
Предполагается, что поле скорости периодично по пространственным переменным с теми же периодами, что и поле внешних сил, и среднее поля скорости задано:
hh v ii = q .
Будем интересоваться потерей устойчивости основного (невозмущенного) стационарного течения общего вида
V = (0, V (xi)), hV i = 0, (1)
которое называется сдвиговым (или параллельным) течением.
Известно, что при достаточно больших значениях вязкости v (малых числах Рейнольдса) основное решение устойчиво. Критическим называется значение параметра v = vc, при котором одно или несколько собственных значений линейной спектральной задачи выходят на мнимую ось. Пусть S2 — замыкание в L2 (П) множества гладких соленоидальных вектор-функций, периодических по пространственным переменным xi, х2 с периодами '1 11 '2 соответс/твеиио. П — ортогоиальиый проектор в L2(n) па подпространство S2 (гидродинамический проектор). Линеаризуя уравнения Навье — Стокса на основном течении (1), получим линейную спектральную задачу в S2;
Ay + iw0y = 0,
A y = -vcnA y + П
∂ϕ yiV (xi)e2 + V(xi) д—
∂x2
e 1 e 2
ния применим схему метода Ляпунова — Шмидта, предложенную В. И. Юдовичем [1]. Сначала рассматривается линейная спектральная задача (2), на втором шаге находятся собственные векторы линейной сопряженной задачи
А*Ф - iШoФ = 0,
V(xi) X f^j +
∂x2 ∂xj j=1 j где A* — гильбертово-сопряженный к оператору A в S2. При исследовании устойчивости относительно длинноволновых возмущений на каждом шаге метода Ляпунова — Шмидта применяются разложения в ряды по малому параметру а.
Впервые длинноволновая асимптотика ( а ^ 0) задачи устойчивости двумерных параллельных пространственно-периодических течений общего вида построена в [2]. При этом поле скорости выражалось через функцию тока, для которой получалась задача Орра — Зоммерфельда. В [3] для построения первых членов асимптотики вторичных автоколебаний рассматривались непосредственно уравнения Навье — Стокса. В [4] с помощью некоторой формализации (применения интегральных операторов типа Вольтерра и вронскианов) получены рекуррентные формулы k-ro члена длинноволновой асимптотики задачи устойчивости (2) стационарных сдвиговых течений с ненулевым средним (1). Настоящая работа посвящена выводу рекуррентных формул k-ro члена длинноволновой асимптотики линейной сопряженной задачи (3). Подробный вывод изложен в [5]. Обоснование асимптотики в данной работе не проводится, но его можно провести, воспользовавшись теоремой о неявной функции для аналитических оператор-функций подобно тому, как это проделано в [2].
-
2. Первые члены асимптотики
Через H обозначим подпространство функций из L2(0,'i), ортогональных единице:
H = f € L2(0,'i): hf i = 0}.
Определим интегральный оператор I : H ^ H по правилу
x
If = j f (s) ds -
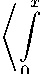
Оператор I — обратный к оператору дифференцирования и вполне непрерывный. Через W(f, g) обозначим вройекнан функций f 11 g:
w (f,g) = fd- - gdf. dx dx
Фигурными скобками будем обозначать отклонение периодической функции от ее среднего значения по периоду {F } = F (x) -hF i. Функция 6 характеризует отклонение скорости от ее среднего значения:
6 " = V - hVi, h6i = 0.
Запишем уравнение (3) в виде системы скалярных уравнений (здесь и в дальнейшем применяются обозначения ст = iw; x = x1, z = ax2)
СТФ1 + Vc
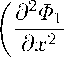
+ a2
д2Ф1 \ ∂z 2
+ aV^ + V (x)
∂z
∂Φ 2
∂x
∂P ∂x ,
СТФ2 + Vc
∂ 2 Φ 2 ∂x 2
2 d2ф2 \ дф 2
+ a O 9 ) + 2aV “S— =
∂z 2 ∂z
-
∂P ∂z
дФ1 + дФ2
hФ2i = 0,
2π j Ф1 dz = 0.
Неизвестные поле скорости Ф и давление P (x,z) будем разыскивать в виде рядов по степеням параметра а;
∞∞
Ф = X Фkak, P = X Pkak.(7)
k=0
Собственные значения ст и критическое значение вязкости vc также представим в виде рядов
∞∞ ст(а) = У^ ст к ак, Vc = v* + ^ Vkak.(8)
k=0
В случае линеаризованного оператора Навье — Стокса линейная сопряженная задача (3) является более вырожденной по сравнению с линейной спектральной (2) — несколько первых членов асимптотики обращаются в нуль. Подставив разложения (7)-(8) в систему (4)-(6) и рассмотрев уравнения при к = 0 и к = 1, несложно убедиться, что выполняются равенства
Po = Ф2 = Ф2 = 0, Ф0 = e-im z,
ф1 = Ф1(z), сто = 0, СТ1 =im hV i.
Для давления P 1 получаем выражение
P 1=q*(x) d?+ < P 1 8
dA q* = -ao(6), ao(6) = —.
dx
Всюду в дальнейшем через ak и q* обозначаются функции, через которые выражаются коэффициенты скорости Фк и давления Pк линейной сопряженной задачи, а ak и qk^ это соответствующие коэффициенты скорости yk и давления Qk линейной спектральной задачи, найденные в [4].
В [4] показано, что коэффициенты разложений по степеням а собственных функций линейной спектральной задачи имеют следующую структуру:
^k =
-
1 dk У1 т/ Vk-1 1
Ц "ДТ I k-1<e)) - — *1’
-
Qk =
1 dk У0 а (РА
Vk - 1 qkW —
νk-2
ν ∗
Q 2 ,
yk =
1 dk y0
ν∗k+1 dzk
ak (#) - у д ^2,
где ak- qk выражаютея норе:;: aj. qj щ hi j 6 k — 1. Слагаемое, содержащее Vk-2 в выражении коэффициентов давления Qk, появляется при четных k > 4.
Коэффициенты разложения собственных значений линейной спектральной задачи и критического значения вязкости при четных k имеют вид [4]
а при нечетных k
"k = о,
k -2
vk-2 = Чт ^0ak-2(^)>,
2 V*
(Ю)
"k =
-
(—im)k
ν∗k-1
Vk-2 = 0.
(И)
Здесь m = 0 — волновое число.
После подстановки разложений (7)—(8) в уравнения (4)-(б) и приравнивания коэффи-
αk k-ro члена асимптотики линейной
сопряженной задачи при k > 2:
-
ν∗
∂2Φ1k ν∗ ∂x2
∂2Φ1k-2
∂z2
-
-
∂Pk ∂x
-
d2Φ01 νk-2 dz2
∂2Φ2k ν∗ ∂x2
-
Φ k-1
-
∂Pk-1
-
- V (x)
k-3
X vj j=2
∂z kX d2фк-j j=2 νj ∂x2
-
-
∂Φ1 k -1 ∂z
∂2Φ1k-j
∂x2
Φ k-1
-
- "k$i(z) - V(x) ^x2
k -3
- X " ^k-j j=3
k-1
2V(x) дф— ∂z
k-2
X "j *k-j j=3
-
k-4
X vj j=2
-
-
∂Φk
1 + ∂x
∂Φ2k-1 ∂z
k-5
X vj j=2
∂2Φ1k-j-2
∂2Φ2 k -2 ν∗ ∂z2
∂2Φ2k-2-j
∂z2
= 0, ( Ф2 ) =0, / фк dz = 0.
∂z2
,
j граница суммы не меньше нижней.
Будем разыскивать решения системы (12)—(14), периодические по x и по z с периодом 2п. Условием разрешимости уравнений (12) и (13) является равенство нулю среднего правой части по переменной х. Осредненное уравнение (12) имеет вид
k
X "j K-j) + hvi j=1
d( фk-1>
dz
Lh( 9$k-1 9 Фk
00 1 2
∂z ∂x
k-2
dL (^k - 2 - j dz2 1
Среднее давления находим из условия разрешимости уравнения (13):
# (P k --) = ^(V(x) ^ dz ∂z
.
Приведем схему нахождения к-го члена асимптотики. Пусть ф(( 1 известно. Тогда из уравнения неразрывности (14) находим Фк:
∂Φk-1
Фк = -I 2 + Фк).
Затем из условия разрешимости уравнения (13) находим среднее давления hPk 1), а из
уравнения (13) — Фк- Далее из условия разрешизкости уравнения (12) находим ак+2. Vk и hФk-1i. Наконец, из уравнения (12) находим Pк. Далее процесс повторяется.
Продолжим нахождение первых членов асимптотики. Пусть к = 2. Так как Ф2 = 0,
то из уравнения неразрывности (14) следует, что Ф^ = Ф-Д). Из (16) получаем, что
dZhP 1i = 0. Тогда, подставив в (13) известное возражение P 1 из (9). приходим к уравне
нию для нахождения Ф^:
∂2Φ22 ν∗ ∂x2
d2Φ01 dz2
9' (x).
Отсюда
Ф2 = - а2(9), a2 (9) = 1 2(ao) = I9.
ν∗ dz
Из условия разрешимости уравнения (12) находим а2 = 0, V2 = h(9')2i, Ф-Д) = 0. Подставив найденные выражения Ф-, Ф— Ф2 в (12) при к = 2, пол учим P 2:
20∗
P2 = - q2(x) + (P2), (2 -I 9'0-hVia2 = 5*-hVД2,(19)
ν dz∂x a2(9) определено в (18). Далее б удем пользоваться обозшхчеппем (П = qn + hVian
Рассмотрим систему (12)—(14) при к = 3. Зная Ф2, из уравнения неразрывности по формуле (17) находим Ф- С учетом условия разрешимости уравнение (13) принимает вид
∂2Φ32 ν ∂x2
-а-Ф2 - 2^ V(x) -
2 ∂z
∂{P2 } - ∂2Φ22
∂z ν1 ∂x2 .
После подстановки P 2 из (19) и Ф2 из (18) в (20) и применения интегрального оператора I дважды, выделим старшие члены относительно производных по z функции Ф-
Ф2 = A Ш b3(9) - Or12ф2 - V1 Ф2, Ь3 = -12 [2V(x)i2Ы + (2(9)].(21)
ν dz νν
Нам понадобится также форма представления Ф2, в которой учтено выражение а—
-
3 __ 1 d Ф1 „*(а\ V1 ,/,2 л*(й\ __ г2 г.»0' * г/д'0
Ф2 = V2TZ3"“3<9) - -Ф2' аз(9) = -I I29 a2- Д "dxj
Выпишем условие разрешимости уравнения (12). Подставив в (15) при к = 3 выражение Φ32 приходим к равенству hVi (Ф?(г) + 5) = -азф0<2) + Ц2 ^ <9'<“3)"> - 2V--2Ф2--I»)
z νzz
Из условия разрешимости уравнения (23) находим аз = im <9(0%)''), vi = 0.
ν∗
Убедимся, что аз из (11) и (24) совпадают, т. е. выполняется равенство
- (ao(a*)"> = (ai(a2 )'' ), (25)
где ai = —I {W(9,9')}. Нам понадобится следующее утверждение.
Лемма (о вронскиане). Для любых непрерывно дифференцируемых '1-периоди-чсскпх по x функций f (x). g(x) h(x) справедлива формула
—2fgh) +
fH
gd-|^=
Лемму легко доказать, дважды применив интегрирование по частям.
Для проверки соотношения (25) воспользуемся выражением "3 (22) и применим лемму о вронскиане:
∗
— (W (9,9'^02\
— ("0 ^y = 2(9'9''a2> — (9'1 9"-2
По свойству вронскиана W(9,9м ' ) = dXW(9,9'). Тогда
2 ∗ 2 ∗
—(dx W (9’в)аУ = -(1 Найдем P3 из уравнения (12) при k = 3. Воспользовавшись условием разрешимости (15), приведем данное уравнение к виду — ∂2Φ31 + V* ч 9 " ∂x2 Подставив в (26) известные Ф3 и ф1, находим третий член асимптотики давления Р3 — — d Ф1 а* (Р3 P = V*2 dz3 q3 (x) + V — ∗ 00∂a3 2 ∗ ∗ I 9dx+ V*"2 — hVia3‘ Рассмотрим систему (12)—(14) при k = 4. Зная Ф3, из уравнения неразрывности по формуле (17) находим Ф4. Воспользовавшись условием разрешимости (16) при k = 4, уравнение (13) перепишем в виде ∂2Φ42 ν∗ ∂x2 —а1Ф2 — 2 V(x) ∂z — 8{P3} ∂z — ∂2Φ22 ν∗ ∂z2 — ∂2Φ22 ν2 ∂x2 . Учитывая найденные ранее выражения Φ22 Φ32 P3 получаем Φ , 4 - 1 d4Φ01 2 V3dz4 ∗ a∗4 ф2, a4(9) = —I2 [2{9'0a3} + q*+ v2a2]. ν∗ Подставив в (15) при к = 4 выражение Ф2 (29), приходим к равенству (V) (ф3(=) + dS) = -^(z) + 4ф (60(04)" - v2a2)) - 2V2dg1.(30) dz ν∗ dzdz Из условия разрешимости уравнения (30) находим а4 = 0, V2 = -m (60((a4)00 - v^T).(31) Убедимся, что v2 из (10) и (31) совпадают, т. е. выполняется равенство (aO(a4)00) - v2(a0a2) = (a2(a2У0),(32) где a2 = -I2{W(1а1,0"У1- 3^ie№. Для проверки равенства (32) применим лемму о вронскиане дважды. Подставим в левую часть (32) выражение a4 из (29) и воспользуемся леммой: (aa((a4)" - v2a2)) = -2^№}) + (601 {600(a*)0}) - 3v2(60a2) = (W(6, 0>3) - 3v2(60a*) = -(ai(a*)00) - 3v2<6°a2>. 33 На втором шаге воспользуемся выражением a* из (22) и вновь применим лемму: -(а1(аз)00) - 3v*(60a2) = 2(ai6"a2) -(aiI{600(а2)0})- 3v2(60а2) = -(W(Iai,6")a2) - 3v2(60a2) = (Ы00а2), что и требовалось доказать. Заметим, что из (33) вытекает еще одно соотношение между коэффициентами линейной и линейной сопряженной задачи: (aa(a4 )00) + (ai(a3)00) + 2v3(aaa2) = 0(34) Учитывая (31), из (30) получаем, что Ф^Д) = 0. Для четных и нечетных к соотношения, аналогичные (34), различны [5]. Применив лемму о вронскиане, при к = 3, 5, 7 приходим к равенствам X (a, (ak—j)"} + 2v2 X (a,ak—2—,) + v4 X (I2a,ak—4—,) j=0 j=0j=0 + (^v2" X (a,+1(ak-3-j)00) = 0, 3 ,=0 а при к = 4, 6 имеем X (a, (ak-,)"} + 2v2 X4 (a,ak—2—,) + v4 X (12a,ak—4-,) j=0 j=0j=0 ( 60a2i XX / z * yo) _ (60a2i2 XX / z зyo + 2v2 2^ \aj (ak-2-j) / = 4v4 / , \aj (ak-4-j) /• ∗ j=0 3. Общий член асимптотики К началу k + 1 итерации при k 6 7 известно [5], что коэффициенты разложений собственных функций линейной сопряженной задачи имеют следующую структуру: Φ1k - ν∗k-2 k0 V1 « '' - νk-3Φ31, ν∗ фк = dkΦ01 ∗ ν∗ k-1 dzk ak - νk-2Φ22 , ν∗ 1 dk Ф0 * P k = ~~ тт qk k-1 dzk k - νk-2 ν∗ { P 2} + (Pk У где ak, qk выражаются через a*, q* при j 6 k — 1- Слагаемое, содержащее Vk-2 в выражении коэффициентов давления Pк, появляется при четных k, удовлетворяющих условию k > 4. Более подробные выражения собственных функций имеют вид где ∗ qk = - фк = - k-3 - X Zj 12 j=3 ν∗ Φ1k-j 1 dk Ф0 ν∗k-2 dzk k-3 - фк = - k-2 j=2 bk = i (ьк-1) X Vj ф; ν∗ 1 j=2 ν∗k-1 - ddzΦk1 b∗k - νk-4 Φ41 ν∗ 1 k-6 νj I2 j=2 ν∗ - νk-3Φ32 ∂2Φ1k-2-j ∂z2 , ν∗j Φ2k-j k-2 ν∗ k-5 - j=3 σν∗jI2Φ2k-j - νν∗jI2 ∂2Φ2k-2-j j=2 ∂z2 , -I2 [2{000 ak-1}+qk-i+ v2ak-2], + v4I 2(ак-з)+ v2bk qk∗ -1 = 9k - hViak, "ak 4 (I{9°Ia2} + ak). (43) Последнее слагаемое в (43) присутствует только при четных k. Так как при k 6 7 известно, что hФ1i = вид ... = hФk 2) = 0, то уравнение (15) принимает k k-1 hvi (<фк-1> + ^к О = -укф0(г) - (900(x)( дФ2 + дФ^В dz x z - d2Φ01 νk-2 dz2 . Условием разрешимости уравнения (44) является ортогональность правой части решению однородного сопряженного уравнения. Пусть k четное. Тогда из условия разрешимости, отделяя вещественную и мнимую части, находим (im)k 2 Г. . , . . 1 . .. , . Zk = 0 vk-2 = fc_1 (^ (ak) к — v* (^ ak-2^ + Д (^ ak-4k(^ a2^ •(45) V* L 2J Сравнивая (45) с (10) и учитывая, что собственные значения и критическое значение вязкости в линейной спектральной и линейной сопряженной задаче совпадают, получим связь между коэффициентами линейной и линейной сопряженной задачи при четных к. <Ж)") — v2 При нечетных к вместо (45) приходим к равенствам Vk-2 = 0, ^k = (-mk [<^0(akП — ^-2)],H") ν∗ а из (И) и (47) вместо (46) получим соотношения <^0(ak )00 > — v2<00ak-2> = —<^ak-2).(48) Так как правая часть (44) равна нулю, то hФk-1i = 0. Заметим, что левые части равенств (46) и (48) можно преобразовать в правые, если применить лемму о вронскиане к — 2 раза. При этом в качестве промежуточных результатов при к 6 7 приходим к соотношениям между коэффициентами линейной и линейной сопряженной задачи (35) и (36). Предположим, что формулы (37)—(43), (45), (47) справедливы при n = к. Докажем, что они выполняются для n = к + 1. Для нахождения Ф^1 воспользуемся (17). Очевидно, Ф^1 находится по формулам (40). (42)-(43). если в них к заменить на к + 1. Для нахождения ф2,+"1 сгруппируем слагаемые в правой части (13). заменив к на к + 1, и преобразуем их по отдельности. С учетом выражения среднего давления (16) и уравнения (20) для нахождения Ф2 получим σ1 Φ k-1 + 2V (x) ∂Φ k-1 ∂z + ∂Pk-1 ∂z = 2 е" ∂Φ k-1 ∂z ∂Φ k-1 ∂z + ∂{Pk-1} ∂z dkΦ01 ∂2Φ2k+1 ∂x2 k-1 - j=2 ν∗k-2 dzk Φ [2{000ak-i} + qkL1] + vk-2 д2ф2 ∂x2. k-1 из (13) и (49) выводим 1 dk+1^1 ν∗kdzk+1 [ — 2{900ak} - qk∗ - ν∗2a∗k-1 - νk-2 д2ф2 ν∗ ∂x2 νj ∂2Φ2k+1-j ν∗ ∂x2 - X Zj фk+1-j j=3 ν∗ k-1 k-4 - νj ∂2Φ2k-1-j j=2 ν∗ ∂z2 , отсюда, находим Ф2+1 по формулам (41)—(43) (заменой к на к + 1). Осредненное уравнение (13) при ak+1 имеет вид (44). если к заменить на к + 1. Из условия разрешимости этого уравнения находим Vk-1 и ak+1- Получим формулы (45), (47) с учетом указанной замены. Тогда hФki = 0. С учетом найденных Vk-1 11 Ok+н а тешже Ф^1 11 Ф^1. замени в в (12) к на к + 1. приходим к уравнению для нахождения давления: дрk+1 дФk+1 дФk д Фk+1 —з— = е —2—+ -^ + hv i —2— ∂x ∂x ∂z ∂x 1 dk+1Ф0 1 dk+1 Ф0 dbk д2Ф1 V—4 "1+^ I(ak-2) — VP izk+rzx— Vk-31x2 * Воспользовавшись известными выражениями Фк, Ф2+1, а также уравнением для нахождения P2. преобразуем (51) к виду ∂Pk+1 ∂x 1 dk+^0 ν∗k dzk+1 - v#2I(a^i)} } + hVi da∗k+1 dx — V4I (ak-2) — v2dhk] + Vk—i dP2 - Vk—3 ν∗ ∂x ν∗ ∂2Φ41 ν∗ ∂x2 + 9M ∂z , причем слагаемые в (52), содержащие Vk-i и Vk—з, отличны от нуля только для нечетных к. Подставив в (52) известные выражения ф1 и Ф^ а также Vk—з, находим Pk+1 по формулам (39), (43), в которых к нужно заменить на к + 1, что и требовалось доказать. Заключение. В настоящей работе выведены рекуррентные формулы для нахождения k-го члена длинноволновой асимптотики линейной сопряженной к задаче устойчивости стационарных двумерных сдвиговых течений вязкой жидкости с ненулевым средним hVi — 0. Получены соотношения между коэффициентами асимптотических разложений линейной спектральной и линейной сопряженной задачи. Пусть отклонение скорости от ее среднего значения {V} является нечетной функцией, тогда 0(x) — нечетная функция. В этом случае из рекуррентных формул следует, что коэффициенты разложения собственных функций сопряженной задачи ak (0), bk (0), Фк (0) четные при к четном и нечетные при к нечетном. Аналогичное свойство коэффициентов асимптотики собственных функций выполнялось и в линейной спектральной задаче. Что касается коэффициентов разложения давления, то в линейной сопряженной задаче при нечетной 0(x) коэффициенты qk — qk+ hViak нечетные при к четном и четные при к нечетном. В то же время, для линейной спектральной задачи аналогичное свойство выполнялось непосредственно для коэффициентов разложения давления qk.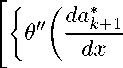
Список литературы К задаче устойчивости сдвиговых течений относительно длинноволновых возмущений
- Юдович В. И. Возникновение автоколебаний в жидкости//Прикл. мат. и мех. 1971. Т. 35, № 4. С. 638-655.
- Юдович В. И. О неустойчивости параллельных течений вязкой несжимаемой жидкости относительно пространственно-периодических возмущений//Численные методы решения задач математической физики. М.: Наука, 1966. С. 242-249.
- Мелехов А. П., Ревина С. В. Возникновение автоколебаний при потере устойчивости пространственно-периодических двумерных течений вязкой жидкости относительно длинноволновых возмущений//Изв. РАН. МЖГ. 2008. № 2. С. 41-56.
- Ревина С. В. Рекуррентные формулы длинноволновой асимптотики задачи устойчивости сдвиговых течений//Журн. вычисл. мат. и мат. физ. 2013. Т. 53, № 8. С. 1387-1401.
- Ревина С. В. Линейная сопряженная к задаче устойчивости двумерных сдвиговых течений вязкой жидкости с ненулевым средним. М., 2014. 47 с. Деп. в ВИНИТИ 11.08.14, № 228-В2014.


