Качественный анализ космологических моделей со скалярным полем

Качественный анализ динамики космологических моделей [1] позволяет проанализировать эволюцию Вселенной в целом и охарактеризовать параметры ее динамики в пределах t ^ ±то . Эта информация очень важна с точки зрения отбора моделей по критериям их асимптотического поведения, которые можно установить без непосредственного построения точных или численных решений уравнения космологической динамики. Такой анализ для моделей с материей в виде скалярного поля и смеси релятивистских жидкостей в предположении их теплового равновесия был проделан в работе [2]. Анализ проводился на энергетической плоскости для различных вариантов выбора зависимости полной энергии скалярного поля (суперпотенциала) от самого поля. В работе были проклассифицированы возможные типы космологических моделей на энергетической плоскости и указаны их основные свойства. Несколько иной качественный анализ космологических моделей с массивным скалярным полем на фазовой плоскости самого скалярного поля был проделан в работах [3–5]. С помощью этого анализа был выявлены некоторые важные особенности поведения таких космологических моделей при ненулевой космологической постоянной как вблизи космологической сингулярности, так и при t ^ то . Успешность такого подхода указывает на то, что с его помощью можно проанализировать гораздо более общий тип моделей. Эта задача частично решается в данной работе. В статье приводится качественный анализ космологических моделей со скалярным полем с произвольным потенциалом самодействия, что расширяет область применения результатов, полученных в работах [3–5], на общий случай моделей со скалярным полем. Затем рассматривается расширенная модель с включением жидкости с заданным баротропным уравнением состояния. Это позволяет получить дополнительные результаты о характере эволюции Вселенной с двумя формами материи, что устанавливает определенную взаимосвязь с моделями, рассмотренными в работе [2].

1.    Космологические модели со скалярным полем и жидкостью

Пространственно-плоские космологические модели со скалярным полем и материей описываются системой уравнения следующего вида [1]:

H ² = ц ( |( ф )² + V ( ф ) + Л + е ) ,

(1.1)

(1.2)

(1.3)

ф + 3 H ф = - V '( ф ),

2 Hi + 3 H ² = 3 ц Рр + 1( ф )² - V ( ф ) - л) .

Здесь a ( t ) - масштабный фактор, H = ail a - параметр Хаббла, ф - скалярное поле, V ( ф ) - потенциал самодействия скалярного поля, ц = 8 п 1(3 M p ) , M P - планковская масса, Л - космологическая постоянная, ε и p - энергия и плотность жидкости, которые предположительно связаны баротропным уравнением состояния:

p = ye • (1-4)

Данная система уравнений в общем случае не интегрируется. Поэтому наиболее полезным способом анализа асимптотического поведения динамики космологических моделей является вычисление их особых (неподвижных точек) и анализа фазовых траекторий вблизи этих точек [6]. Эффективность такого анализа зависит от возможности представить уравнения модели в форме динамической системы, то есть в форме системы уравнений первого порядка по времени и получения исчерпывающей информации относительно ее особых точек. Эта возможность определяется сложностью модели, то есть числом включенных в нее материальных компонент и метрики. Один из вариантов такой модели и был исследован в [4,5]. Мы начнем анализ с общего случая скалярного поля с произвольным потенциалом самодействия V ( ф ) , а затем будем включать в другие элементы общей модели, соответствующей (1.1)-(1.3).

2.    Космологические модели со скалярным полем

Пространственно-плоские космологические модели со скалярным полем описываются системой уравнений следующего вида:

H ² = ц ( 1( ф )² + V ( ф ) + д ] , ф + 3 H ф = - V '( ф )•

(2.1)

(2.2)

Уравнение (1.3) в этом случае является следствием первых двух. Из этой системы можно исключить параметр Хаббла H . Из первого уравнения находим:

H = ± ц ( 2( ф )² + V ( ф ) + д ] •

(2.3)

В этом соотношении мы оставим для анализа только знак + перед квадратным корнем, поскольку нас будет интересовать только расширяющиеся космологические модели с H >  0 . Подставляя это соотношение во второе уравнение, получаем:

ф + 3 фц ( 2( ф )² + V ( ф ) + д ] = - V '( ф ).

(2.4)

Это уравнение теперь можно представить в виде двумерной динамической системы первого порядка:

ф = P ( ф , ё ) = ё ,

(2.5)

(2.6)

ё = Q ( ф , ^ ) = - 3 ^[ц ( ^ ²12 + V ( ф ) + д ] - V '( ф )•

Особыми или неподвижными точками системы являются такие точки ( ф_i , ^ i ) на фазовой плоскости ( ф , ё = ф ) , в которых выполнены условия:

P ( ф i , ^ i ) = Q ( ф i , ^ i ) = 0.

Для системы (2.5) соответствующие точки определяются решениями уравнений:

^ i = 0, V '( ф i ) = 0, , i = 1..... N

(2.7)

Следовательно, неподвижными точками всех таких моделей являются экстремумы потенциала самодействия V ( ф ) , число которых обозначено через N . Для анализа характера поведения Вселенной при асимптотическом приближении к неподвижным точкам следует вычислить значение масштабного фактора, исходя из формулы (2.3). В результате имеем:

H i = V ц (Л + V ( ф i )), i = 1..... N •

(2.8)

Согласно общей идеологии качественного анализа, неподвижные точки могут быть притягивающими или отталкивающими в зависимости от того, приближаются или удаляются от этих точек траектории (интегральные кривые) системы при t ^ то . Для выяснения этого обстоятельства необходимо провести анализ поведения бесконечно малых возмущений вблизи неподвижных точек.

Представим параметры модели в следующем виде: ф = ф . + x и £ = Ч + у , где x и у - возмущения первого порядка малости, зависящие от t , а φ_i и ξ_i - значения функций системы в неподвижных точках. Согласно общей теории возмущений, уравнения для x и y будут иметь вид:

.   д Р ( ф . , Ч )     д Р ( ф . , Ч )

(2.9)

(2.10)

x =----------x + дф.

. д Q ( ф . , Ч )     д Q ( ф . , 4 )

У = —57--x + —55

∂φi

Решение системы ищется в виде: x = Ae ^{X t} , у = Be ^{X t} , где характеристические числа X находятся из решения алгебраического уравнения:

det(

дР (ф1 , 41) _ дф. X дQ ( Ф1 , 4.)

∂φ i

дР ( ф 1 , ^i )

∂ξi dQ (ф. , 4.)

∂ξ i

X .| = °"

Для рассматриваемого случая:

д Р ( ф . , Ч ) ∂φ i д Q ( ф . , Ч )

∂φ i

_   д Р ( ф . , Ч )

0   д^.     1

= - V4ф ), д 0 (^>

∂ξ i

- з V ц ( V ( ф ) + Л ) •

(2.11)

(2.12)

(2.13)

Отсюда уравнение для характеристических чисел будет иметь такой вид:

X ² + 3 X V ц ( V ( ф . ) + Л ) + V Ч ф . ) = 0.

Таким образом:

X ± = - 2 [V Ц ( V ( ф 1 ) + Л ) ± V Ц ( V ( ф 1 ) + Л ) - 4 Vч ф 1 )/9 ] =- 3 H i ± V 9 H i /4 - V "( ф , )•     (2.14)

Устойчивость неподвижной точки определяется знаками вещественной части всех характеристических чисел системы в этой точке. Устойчивыми или притягивающими точками будут те, для которых вещественные части X ₊ и X _- будут отрицательными. Для этого достаточно, чтобы выполнялось одно из условий:

• (I)    ц(V(ф.) + Л) > (4/9) VЧф) > 0,

• (II)    0 < ц(V(ф.) + Л) < (4/9) VЧф)•                       (2.15)

3.    Потенциал Хиггса

Отметим то обстоятельство, что при Л = 0 и V ( ф . ) = 0 , особая точка представляет собой центр. Учитывая то, что величину V ( ф . ) + Л можно рассматривать как эффективную космологическую постоянную, можно утверждать, что признаком равенства нулю эффективной космологической постоянной является асимптотическая осцилляция поля вблизи φ i с ненулевой амплитудой, по крайней мере в нулевом порядке теории возмущений. Частота этих осцилляций определяется величиной ^ ₀ = ^ | 9 H i /4 - V " фф . ) | . Эти осцилляции должны прослеживаться не только в значениях самого поля, но и в величине параметра Хаббла. Таким образом, обнаружение осцилляций величины параметра Хаббла на фоне фридмановской или де-Ситтеровской стадий эволюции может быть признаком выполнения неравенства (II), то есть 0 <  ц ( V ( ф . ) + Л ) <  (4/9) V " фф ) . Период осцилляций и их амплитуда в параметре Хаббла могут быть достаточно большими. В силу этого, есть вероятность того, что локальное увеличение параметра Хаббла может в эксперименте восприниматься как ускоренное расширение Вселенной при выполнении условия (II).

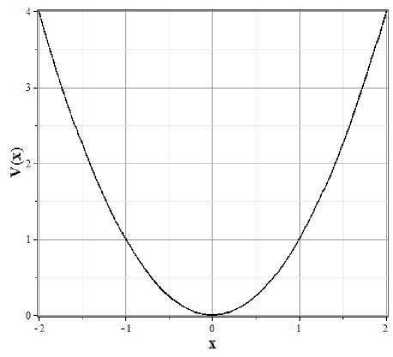
Потенциал Хиггса определяется соотношением:

V ( ф ) — аф ⁴ - вФ ² + c ,

(3.1)

где а , в , c - положительные постоянные. Этот потенциал имеет три экстремума:

ф 1 — 0, ф 2 — ^ в /(2 а ), ф з — -^ в /(2 а ).

Число c обычно определяется из условия, что в минимумах ф ₂ , ₃ значение потенциала равно нулю:

c — в ²/(4 а ),

Условие V ( ф ) >  0 необходимо для выполнения принципа энергодоминантности при всех ф в процессе эволюции. В экстремумах находим значения самого потенциала и второй производной:

V ( ф i ) — в ²/(4 а ), V "( ф i ) — - 2 в , H 1 — ^ Р ( 4 | + л ) , V ( ф 2,3 ) — 0, V "( ф 2,3 ) — 4 в , H 2,3 — V pA .

(3.2)

В результате:

( i — 1)      Л ± —

( i — 2,3)     Л ± —

| \]p (4 а ^+Л ) ± \ЖЧ^{+ в 9} I' 2 [ \^{/р Л} ± ^ ^p A^- 8 ^ /3] .

Из последних соотношений следует, что точка ф ₁ — 0 является неустойчивой при t — то , поскольку одно из характеристических чисел положительно при всех допустимых параметрах системы и потенциала, то есть при Л >  0 и а >  0, в >  0 . Однако эта точка является устойчивой в обратном времени, то есть при t — -то . Следовательно, для данного типа потенциала выход из точки t — -то устойчиво происходит в виде инфляционного роста масштабного фактора, поскольку в этом случае H i >  0 вблизи этой точки.

Две другие точки устойчивы, поскольку при всех параметрах системы и потенциала вещественные их части отрицательны. В этом случае значения масштабного фактора определяются исключительно значением космологической постоянной. В результате, если космологическая постоянная ненулевая, то реализуется сценарий ускоренного расширения в форме вторичной инфляции:

a ~ e Vm t , q — aa — i, t — то . a ²

В случае нулевой космологической постоянной реализуется сценарий Фридмана:

a ~ t ^v , Q — aa — 1, H ( t ) ~ t a ²

—* H i — 0, t —* <ТО .

Тип устойчивых точек зависит от соотношения значений космологической постоянной и параметра потенциала b . Именно, в случае Л = 0 обе точки представляют собой центр:

Л ± — Л ± — + i |^8 в 3.

(3.3)

В случае 0 <  Л <  8 в /3 - фокус:

Л ± —

- 2 [ V p л ± i ^ | p Л - 8 в /3 | ] ,

(3.4)

и в случае Л >  8 в /3 - узел (оба корня - вещественные и отрицательные). Таким образом, возможность наблюдать осцилляции существует в случаях (3.3) и (3.4). Как уже отмечалось, наличие осцилляций в параметре Хаббла может восприниматься как ускоренный режим эволюции.

4.    Модель со скалярным полем и жидкостью

В качестве следующего примера рассмотрим модель с жидкостью. Вычислим из первого уравнения (1.1) плотность энергии жидкости:

E = ЦH2 - (2(ф)2 + V(ф) + л),(4.1)

и подставим в третье уравнение, полагая при этом p = ye .В результате, система уравнений после введения переменной ё = ф , принимает такой вид:

Ф = P (ф, ё, Z) = ё,

, „     3( y + 1) -> Ц ( Y — 1)       -( y + 1) ( А

H = R (ф, ё, Z) = - —H2 +       ё2 + Ц       V (ф) + Л),

ё = Q(ф, ё,Z) = -3ен- V'(Ф).

Неподвижные точки этой модели при у = — 1 вычисляются из условий:

ё1 = о, Hi = VЦ(Л - V(фi)), V'(фi) = 0.

Как и в модели с одним скалярным полем, неподвижные точки соответствуют экстремумам потенциала φ i , а значения масштабного фактора в неподвижных точках вычисляются по тем же формулам (2.8). Из соотношения для H i следует, что вещественные значения H i в стационарных точках будут существовать при условии неотрицательности подкоренного выражения для H i , то есть:

0 <  Л - V ( ф i ).

В силу требований принципа энергодоминантности [1] это условие выполняется всегда. Отметим также, что неподвижные точки (4.6) при H i >  0 соответствуют экспоненциальному расширению Вселенной, то есть асимптотическому ускоренному расширению:

a = a ₀ e^Hit , Q = aa = 1, t — то .

a ²

В случае H i = 0 , что возможно при одновременном выполнении условий Л = 0 и V ( ф_i ) = 0 , система будет переходить асимптотически к фридмановскому сценарию:

a ( t ) ~ t ^v —* H ( t ) ~ t —* 0, t —* <то .

Отсюда следует, что для того, чтобы реализовался сценарий с ускоренным расширением Вселенной в асимптотике при t — то достаточно, чтобы выполнялись условия Л - V ( ф_i ) >  0 и y > - 1 .

Особыми случаями являются модели, соответствующие условию y = - 1 . В этом случае особая точка определяется двумя соотношениями:

^ i = 0, V '( ф i ) = 0,                                           (4.6)

а значение H i не определено. В силу этого в асимптотике эти модели допускают все возможные типы расширения Вселенной.

Используя (4.6), можем вычислить в неподвижных точках значения параметров жидкости:

E i = -H _z ² µ ⁱ

- V ( ф i ) - Л = 0.

(4.7)

Отсюда следует, что при условии выполнения принципа энергодоминантности и расширения Вселенной в асимптотике E i = 0 , то есть эволюция Вселенной стремится к состоянию с нулевой плотностью жидкости.

Вычисляем производные в неподвижных точках:

∂P     ∂P     ∂P dii " 0 дёй "dH-

∂ Q ∂φ i

- v "( Ф - ),

∂ Q ∂ξ i

-

∂ Q

3Hi, dHi " 0

∂R     ∂ Q     ∂Q дф-" 0 дё?" 0 dH-

- -( y - 1) H i .

Уравнение для характеристических чисел в результате будет иметь такой вид:

(X + 2( у + 1) H i^ (л ² + 3 X H + V "( фi )) = 0.                         (4.8)

Эта система имеет три корня:

X о = - 3( у + 1) H i ,

X ± =

3 H

—- ±

- V "( Ф i ).

(4.9)

Сравнивая эти соотношения с (2.14) можно видеть, что последние два характеристических числа в точности совпадают с характеристическими числами линеаризованной модели, только со скалярным полем. Отличием является только наличие в системе дополнительного третьего не положительного характеристического числа X ₀ при у > - 1 . Следовательно, все основные выводы относительно асимптотического поведения космологической модели с жидкостью и скалярным полем в случае у > - 1 остаются теми же, что и в случае наличия только скалярного поля. В случае же у < - 1 все особые точки оказываются неустойчивыми.

5.    Численный анализ моделей

5.1.Массивноескалярноеполе

Для численного анализа сначала выберем потенциал в форме массивного скалярного поля:

V = m2 ф2, где m - параметр размерности массы кванта поля. Вводя безразмерные переменные:

x = ф/фо, у = $/$о, z = H/Hо, т = t/ Tо, где масштабы выбраны следующим образом:

50 = mц1 2, ф0 = ц1 2, T0 = m-1, Hо = m, система уравнений (4.2) приводится к безразмерному виду:

x = у,

. _ 3( у + 1) 2 ( Y - 1) 2 3( у + 1)/ 2

z =    2— z +   2— y +   2— v + Л), у = Q(ф, $, Z) = -3yz - 2x.

Здесь:

Л = Л ц / m ².

Как видно, единственным существенным параметром обезразмеренной системы с массивным скалярным полем является величина космологической постоянной.

На рисунке 1 представлены типичные графики эволюции нормированного поля x ( t ) = ф ( t)^ ц и нормированного параметра Хаббла z ( t ) = H ( t )/ m для массивного скалярного поля на интервале времени t е [0,100 m ^{- 1}] . Для численного анализа выбрано значение параметра баротропы, равное его значению для изотропного электромагнитного излучения, то есть у = 1/3 . Как показывает анализ, изменение у в пределах 0 <  у <  1 меняет динамику модели незначительно.

Начальные условия выбраны такими x (0) = 1, у (0) = - 0.1, z (0) = 1 , а значение нормированной космологической постоянной принято равным Л = 0.0001 . В соответствии с этим, значение H ₀ в стационарной точке должно быть равно z ₀ = Va, поскольку значение потенциала самодей-ствия в особой точке равно нулю.

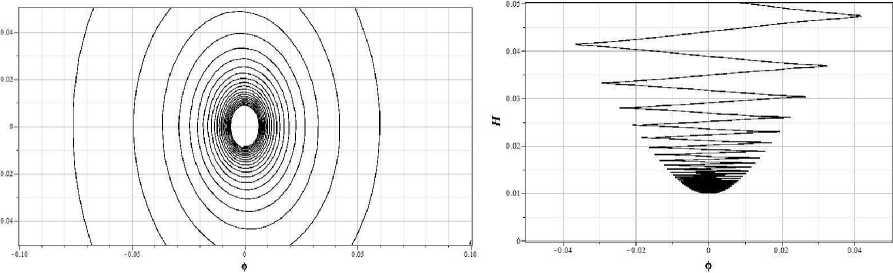
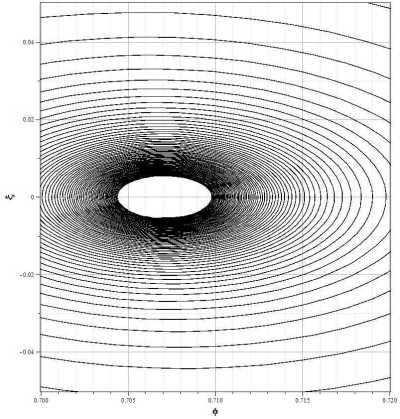
На рисунке 2 представлены фазовые портреты системы на двух плоскостях x - у и x - z , то есть нормированные фазовые портреты ф - ф и ф - H . Для иллюстрации того, что значения параметров модели стремятся к значениям в особой точке, на рисунке 3 приведены отдельно области графиков вблизи особых точек. Из рисунка 3b видно, что масштабный фактор стремится

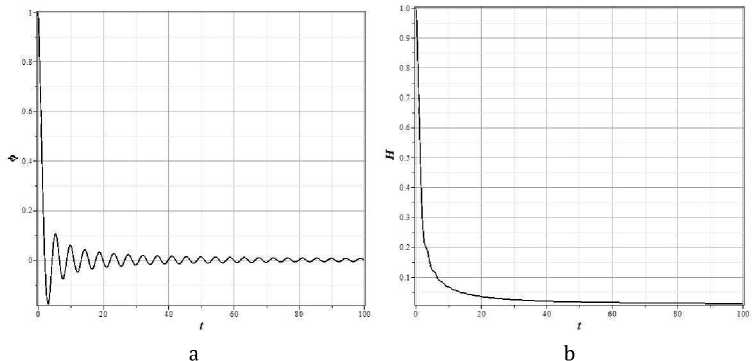
Рис. 1. Графики эволюции переменной x ( t ) (a) и z ( t ) (b) со временем для потенциала массивного скалярного поля и Y = 1/3 .

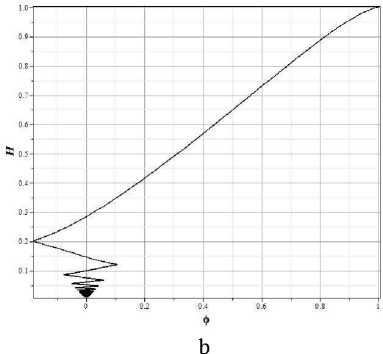
Рис. 2. Фазовые портреты x - y (a) и x - z (b) для потенциала массивного скалярного поля и y = 1/3 .

ab

Рис. 3. Области фазовых портретов x - y (a) и x - z (b) вблизи особых точек для потенциала массивного скалярного поля и y = 1/3

к значению z 0 = V Л = 0.01 . Рисунок 3a демонстрирует асимптотическое стремление не к фокусу в точке (0,0) , как это следует из анализа в первом порядке теории возмущений, а скорее к

a

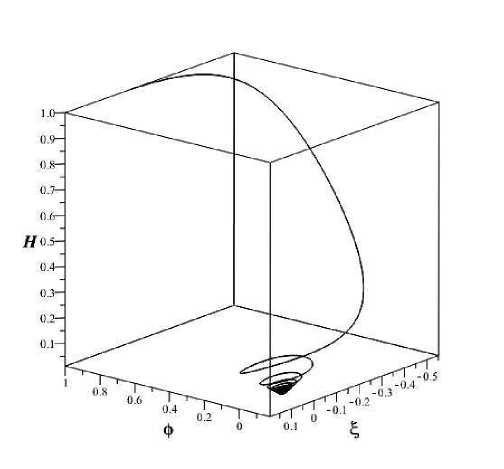
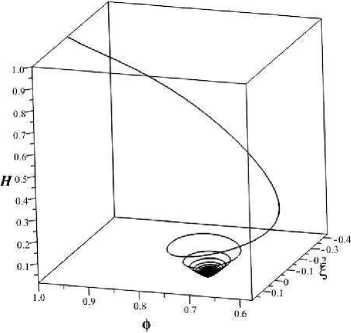
Рис. 4. Фазовый портрет x - у - z и потенциал самойдействия массивного скалярного поля ( у = 1/3 )

b

предельному циклу. Последнее можно проверить, лишь переходя к анализу во втором порядке теории возмущений.

Для иллюстрации общего поведения рассматриваемой системы на рисунке 4 приведен фазовый портрет в 3D при тех же начальных условиях.

5.2.ПотенциалХиггса

В безразмерном виде потенциал Хиггса (3.1) будет иметь вид:

V ( x ) = v x ⁴ - x ² + 1/(4 v ).

Здесь параметр массы m , фигурирующий в модели со скалярным полем, выбирается следующим образом:

m = V ^е ■

В этом случае: v — а и система уравнений примет следующий вид:

x — у,

. _ 3(Y + 1) 2 (Y -1) 2 3(Y + Ш 42 z —--z +--у +--I vx — x +---+ ЛI, у — Q(ф, £,Z) —-3yz - 4vx3 + 2x■

• 5.2.1.    Параметр баротропы у — 1/3

На рисунках 5 – 8 представлены графики, аналогичные графикам для случая массивного скалярного поля. Представленные численные решения соответствуют тем же начальным условиям x (0) — 1, у (0) — - 0.1, z (0) — 1 и тому же выбору параметров системы с одним дополнением. Параметр v выбран равным 1 . Соответствующий график потенциала самодействия представлен на рисунке 11. Можно видеть, что общее поведение моделей вблизи особых точек отличаются не значительно друг от друга.

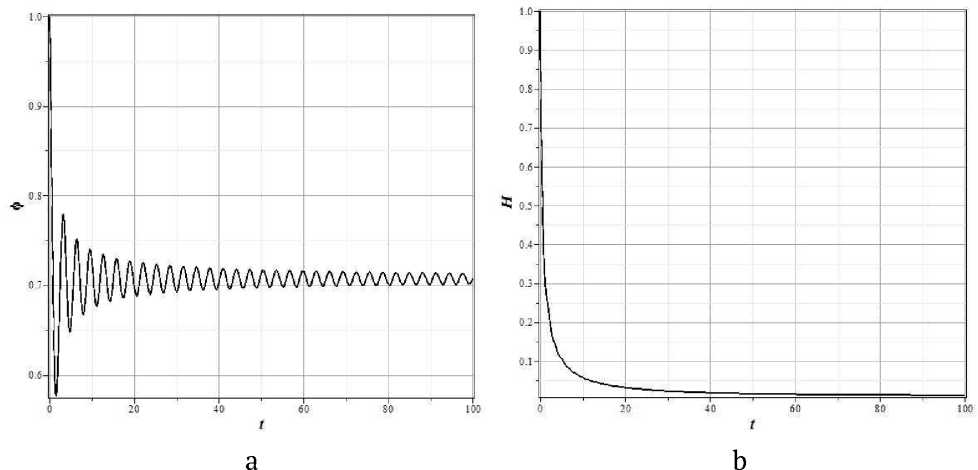
Рис. 5. Графики эволюции переменных x ( t ) (a) и z ( t ) (b) для потенциала Хиггса и у = 1/3 .

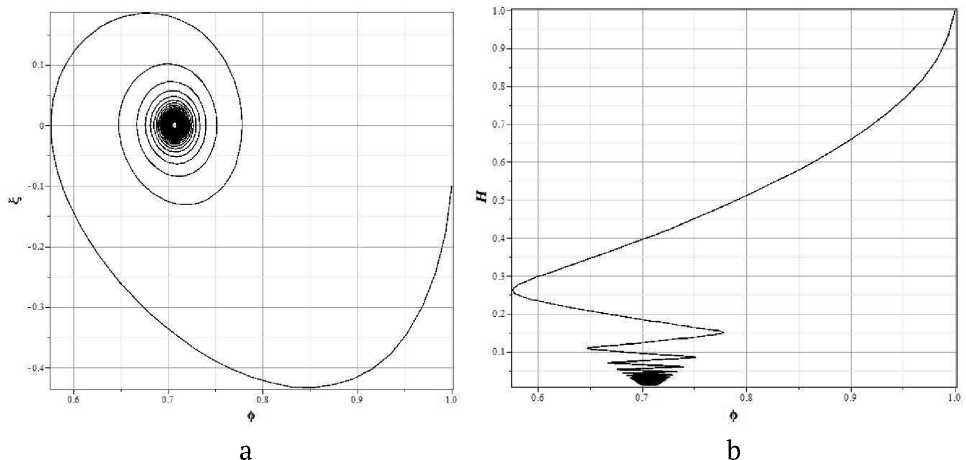
Рис. 6. Фазовые портреты x - y (a) и x - z (b) для потенциала Хиггса и y = 1/3 .

a

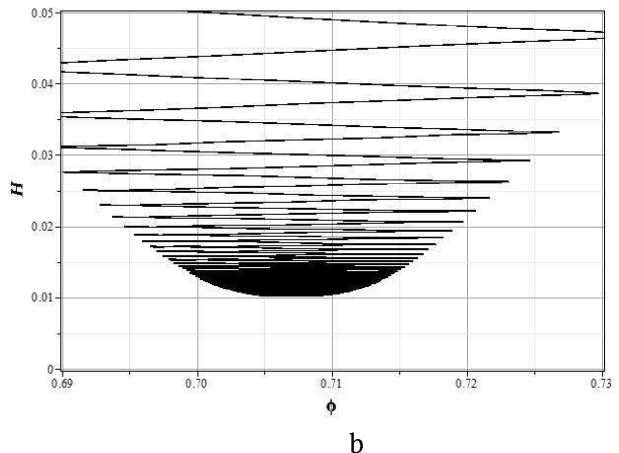
Рис. 7. Области фазовых портретов x - y (a) и x - z (b) вблизи особых точек для потенциала Хиггса и у = 1/3

a

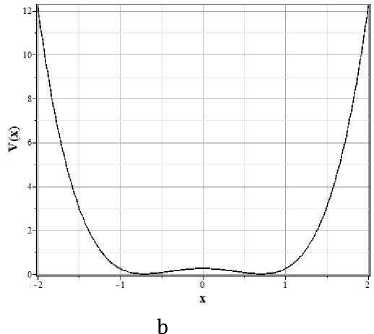
Рис. 8. Фазовый портрет x - у - z (a) и потенциал самодействия Хиггса (b)( у = 1/3 )

• 5.2.2.    Параметр баротропы у = — 1

На рисунках 9 – 11 представлены графики для случая потенциала Хиггса, но для особого значения параметра баротропы, равного у = — 1 . Представленные численные решения соответствуют тем же начальным условиям x (0) = 1, у (0) = - 0.1, z (0) = 1 и тому же выбору параметров системы, что и в предыдущем случае. Общее поведение модели вблизи особых точек теперь отличается существенно. Значение масштабного фактора в асимптотике теперь отличается существенно от значения, которое бы он имел при у = - 1 - Особая точка представляет теперь не фокус или, возможно, предельный цикл, как это можно видеть в предыдущих моделях, а узел.

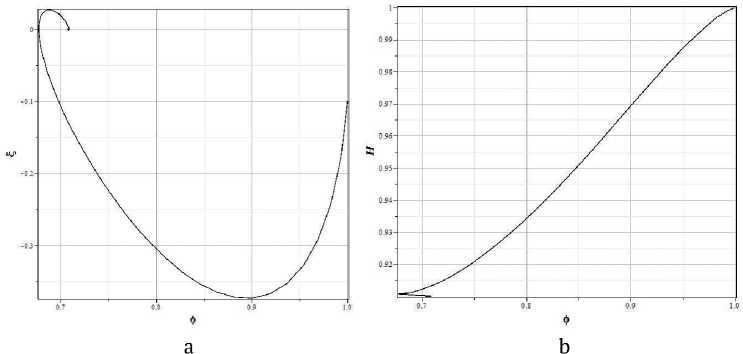
Рис. 9. Фазовые портреты x - у (а) и x - z (b) для потенциала Хиггса и у = - 1 -

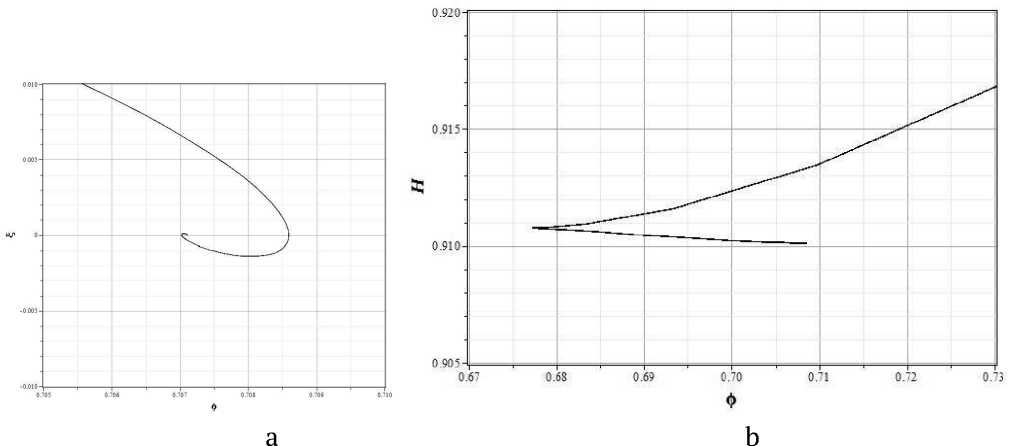
Рис. 10. Области фазовых портретов x - y (а) и x - z (b) вблизи особых точек для потенциала Хиггса и у = - 1

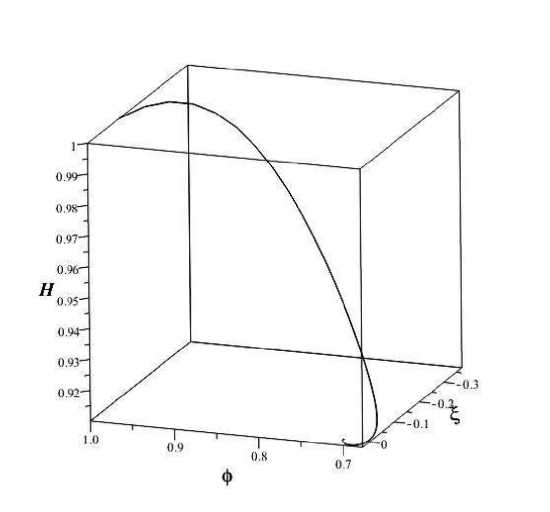
Рис. 11. Области фазовых портретов x - y - z для потенциала Хиггса и у = - 1

Заключение

Проведенный качественный анализ динамики космологических моделей с потенциалом са-модействия скалярного поля общего вида и жидкостью с баротропным уравнением состояния показывает, что общее поведение всех таких моделей вблизи устойчивых особых точек незначительно отличается от поведения системы с одним скалярным массивным полем [3–5]. Численный анализ подтверждает этот общий вывод. Существенным образом динамика системы отличается лишь в случае параметра баротропы у = - 1 . В процессе анализа численного решения привлекает внимание тот факт, что, по крайней мере, для случаев у >  0 , на фазовой плоскости ф - ф система не стремится к стационарной точке, что должно быть следствием выводов, полученных в первом порядке теории возмущений. При Л = 0 точки должны быть фокусами. Однако, как показывает численный анализ, траектории системы выходят, по всей видимости, на предельный цикл. Этот важный вывод должен быть проверен с привлечением анализа во втором порядке теории возмущений или другими способами. Как было отмечено, наличие предельных осцилляций масштабного фактора в рассматриваемых моделях, особенно в случае выхода системы на предельный цикл, может восприниматься в эксперименте как ускоренное расширение на определенных участках эволюции. Это может привести к новой интерпретации наблюдаемого современного ускоренного расширения Вселенной, как участка осцилляции масштабного фактора с ростом параметра Хаббла H ( t ) .

Автор искренне благодарит Игнатьева Ю.Г. за полезное обсуждение темы данной работы.

Работа выполнена при поддержке Министерства Образования и Науки РФ (в рамках Государственного задания и проекта № 14.Z50.31.0015) и за счет средств субсидии, выделенной в рамках государственной поддержки Казанского (Приволжского) федерального университета в целях повышения его конкурентоспособности среди ведущих мировых научно-образовательных центров.