Качественный анализ моделей происшествий с помощью диаграмм влияния

Одним из основных достоинств моделирования происшествии с помощью диаграмм влияния различного типа является возможность их качественного анализа (уточнения существующих представлений об условиях возникновения и предупреждения исследуемых событий), а также удобство последующей формализации и перехода от качественного анализа к количественному (от семантических моделей к семиотическим системам).

Подобно потоковым графам, качественный анализ которых состоит в рассмотрении условий достижения конкретного состояния – терминального узла, соответствующий анализ дерева происшествий связан со вскрытием возможности появления или не появления головного события – происшествия конкретного типа. Легче всего устанавливать данные условия путем выделения из всего массива исходных предпосылок двух подмножеств, реализация которых либо приводит, либо не приводит к возникновению головного события. Такие подмножества часто делятся на аварийные сочетания предпосылок, образующие в совокупности с условиями их появления каналы прохождения сигнала до этого события, и отсечные сочетания , исключающие условия формирования таких путей к головному событию.

Однако самым удобным способом выявления условий возникновения и предупреждения происшествий является выделение из подмножеств так называемых «минимальных сочетаний событий», т.е. тех из них, появление которых минимально необходимо и достаточно для достижения желаемого результата. Минимальное пропускное (аварийное) сочетание обычно рассматривается как набор исходных предпосылок, осуществление обязательно всех элементов которого достаточно для появления головного события (прохождения сигнала до него).

В одном дереве происшествий может быть несколько минимальных сочетаний предпосылок, дающих наиболее существенный вклад в реализацию исследуемого исхода.

Для отражения существенности вклада отдельных предпосылок и их сочетаний иногда вводятся показатели их значимости и критичности. Эти категории могут указывать на вероятности наступления таких состояний моделируемого процесса, при которых появление отдельных событий или их наборов оказывается наиболее существенным, значимым, а иногда и критичным – минимально необходимым и достаточным по отношению к условиям возникновения или предупреждения головного события. Используемые в настоящее время критерии значимости и критичности, а также способы их расчета и практического применения, можно обнаружить, например, в работах [1, 2].

Результаты качественного анализа полученных моделей позволяют уточнить условия, а иногда и закономерности исследуемых процессов, однако оценки их числовых характеристик могут быть получены лишь на следующем этапе – при проведении количественного анализа. Исходными данными для него служат не только структура дерева происшествий, но и числовые характеристики или законы распределения (плотности вероятности или функции принадлежности) переменных, задаваемых узлами или вершинами этой модели. Подготовительным этапом к количественному анализу является дальнейшая формализации – получение с помощью алгебры событий и булевых преобразований таких аналитических выражений, которые учитывают все рассматриваемые в модели переменные и связи между ними.

Известным средством аналитического представления заданного деревом процесса служат так называемые структурные функции. Они позволяют выразить достоверность появления головного события в зависимости от соответствующих характеристик исходных предпосылок. При этом в качестве объективной или субъективной ее меры используются соответственно вероятности – Prob и возможности – Poss. Заметим, что содержание символа P е {Prob, Poss} обычно определяется характером исходных данных.

Предположим, что в дереве происшествий выявлено «а» минимальных пропускных сочетаний, в каждом i -ом из которых содержится « m » постулируемых исходных событий - предпосылок. Следовательно, можно построить дерево (рис. 1а), включающее в себя « а » исходных предпосылок, объединенным логическим условием « ИЛИ ».

В случае, когда дерево происшествий содержит в себе ровно « b » минимальных отсеченных сочетаний событий с n k постулируемыми исходными предпосылками в каждом из них, его можно упростить подобным образом до модели, показанной на рис. 1б. Так как для возникновения происшествия необходимо отсутствие одновременно всех минимальных отсечных сочетаний, то исходные события нового дерева объединены уже логическим условием « И ». В свою очередь, каждое событие этой упрощенной модели образовано логическим сложением составляющих его постулируемых исходных событий дерева-оригинала.

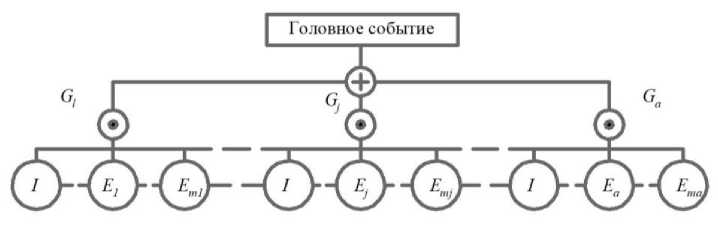
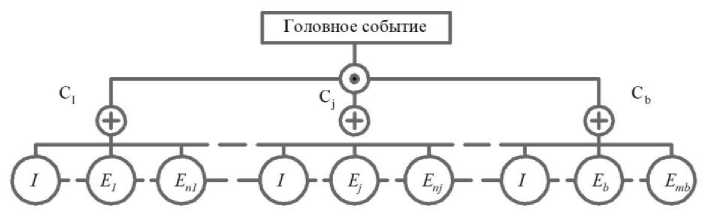
б)

Рис. 1. Модификация дерева происшествий: а) Первое, j-ое и а -ое минимальные пропускные сочетания; б) Первое, j-ое и b -ое минимальные отсеченные сочетания

Легко показать, что, при использовании минимальных сочетаний событий, для расчета вероятности возникновения происшествий необходимо соблюдать следующие условия. Если качественный анализ обеспечивается минимальными пропускными сочетаниями предпосылок, то в новом, упрощенном дереве они должны логически складываться. Если же в ходе него получены минимальные отсечные сочетания, то в новой модели эти сочетания событий должны перемножаться, т.е. объединяться логическим условием « И».

На этом основании можно утверждать о справедливости таких выражений для структурных функций обеих деревьев: ami

Q = 1 -П (1-П P)(1)

i=1

bnk

Q = П[1 -П (1 - Pki)].(2)

k=1

где  a,  b – количество соответственно минимальных пропускных минимальных отсечных сочетаний;

m i , n k – число исходных предпосылок в каждом i -ом из пропускных и каждом k -ом из отсечных минимальных сочетаний исходных предпосылок к происшествию.

Числовые значения вероятностей или возможностей возникновения постулируемых исходных событий и законы распределения (функции принадлежности) связанных с ними параметров определяются, исходя из проектных или статистических данных по интенсивности отказов производственного оборудования или соответствующим показателям ошибок работающих.

В случае отсутствия точечных количественных оценок вероятности или возможности появления исходных событий-предпосылок (ошибок, отказов и нерасчетных внешних воздействий), необходимо воспользоваться методом статистического или имитационного моделирования. Сведения о виде закона распределения – плотности вероятности случайных величин или функции принадлежности лингвистических переменных, а также их числовых характеристиках могут быть получены экспертным путем.

Проиллюстрируем работоспособность изложенных методов на конкретном примере исследования аварийности и травматизма. Предположим, что разработана автоматизированная технология залива горючего в транспортное средство. Данный процесс контролируется одновременно системой дозирования и человеком-оператором; при этом насос может быть отключен либо автоматически – по сигналу расходомера или датчика уровня, либо вручную – по команде оператора.

Нам требуется оценить, а в последующем и обеспечить требуемый уровень пожаро- взрывобезопасности заливки. Количественным показателем её уровня выбрана вероятность возникновения пожара по причине несвоевременного отключения насоса. Будем считать, что пожаро- взрывоопасность данного процесса обусловлена возможностью возникновения интенсивной экзотермической реакции окисления горючего в результате разгерметизации баков и его соприкосновения с окислителем или открытым огнем. Учитывая возможность обеспечения и контроля гарантированной герметичности коммуникаций (принципиальное допущение). основное внимание уделим проливам из баков транспортного средства – вследствие их переполнения. При этом будем иметь ввиду, что проливы способны изменить электрическое сопротивление изоляции токоведущих частей и вызвать короткое замыкание в электросиловых цепях, а это, в свою очередь, приведет к созданию условий, необходимых и достаточных для возникновения пожара и взрыва. Возможная модель аварии приведена на рис. 2.

Пожар вследствие пролива горючего, переполнившего бак по причине излишне продолжительной работы насосов из-за их неотключения вовремя

К

Команда на отключение не поступила

Команда на отключение не осуществлена

Н

САВД нс выдала команды

Оператор нс выдал команды

А

Оператор не пытался отключить насосы

Отказ средств выдачи сигнала

Оператор не среагировал на отказ САВД

Отказ средств передачи сигнала

Оператор не смог отключить насосы вовремя

Рис. 2. Модель возникновения пожара:

САВД – система автоматической выдачи дозы

Модель имеет промежуточные события, помеченные латинскими 6yквами, тогда как в нижней части дерева кругами с цифрами показан постулируемые исходные события-предпосылки, наименования и нумерация которых приведены в таблице.

Таблица

Постулируемые исходные данные модели

№ п/п	Наименование событий или состояний модели
1.	Система автоматической выдачи дозы (САВД) оказалась отключенной (ошибка контроля исходного положения)
2.	Обрыв цепей передачи сигнала от датчиков объема дозы
3.	Ослабление сигнала выдачи дозы помехами (нерасчетное внешнее воздействие)
4.	Отказ усилителя-преобразователя сигнала выдачи дозы
5.	Отказ расходомера (измерителя потока горючего)

6.	Отказ датчика уровня в баке горючего
7.	Оператор не заметил световой индикации о неисправности САВД (ошибка человека)
8.	Оператор не услышал звуковой сигнализации о неисправности (неисходном состоянии) САВД
9.	Оператор не знал о необходимости отключения насоса по истечению заданного времени
10.	Оператор не заметил индикации хронометра об истечении установленного времени заправки
11.	Отказ датчика времени заправки (хронометра)
12.	Отказ автоматического выключателя электропривода насоса
13.	Обрыв цепей управления приводом насоса подачи горючего

Качественный анализ дерева происшествий, приведенного на рис. 2, позволяет выделить три ветви прохождения сигнала к головному событию: АВСK EFGKH L , а также указать связанные с ними минимальные проходные и отсечные сочетания исходных предпосылок. Очевидно, что возникновение пожара (достижение головного события) равносильно появлению любой из двух предпосылок верхнего уровня K или L , что, в свою очередь, эквивалентно произведению событий предпосылок второго уровня C и H или сумме исходных предпосылок 12 и 13 нижнего, т.е. постулируемого уровня.

Подобным образом исследуются условия достижения сигнала до событий С и H , рассматривая их как головные для ниже расположенных событий и наборов. В результате можно выделить 27 минимальных пропускных сочетаний постулируемых исходный событий: из них 20 штук – по два события; 1·7, 1·8, 1·9, 1·10, 111, 2·7, 2·8, 2·9, 2·10, 2·11, 3·7, 3·8, 3·9, 3·10, 3·11, 4·7. 4·8, 4·9, 4·10, 4·11; пять – по три: 5·6·7, 5·6·8, 5·6·9, 5·6·10, 5·6·11 и два – по одному событию: 12 и 13.

Предупреждение возникновения рассматриваемого происшествия может быть достигнуто нарушениями вышеуказанных условий, т.е. пресечением возможности прохождения сигнала до головного события. Это достигается исключением одновременно обеих предпосылок первого (верхнего) уровня K и L, что равносильно недопущению любой из предпосылок второго уровня C и H и – сразу двух постулируемых исходных событий 12 и 13. Следовательно, если анализировать аналогичным путем условия пресечения сигнала от исходных предпосылок до событий С и H, то легко установить три минимальных отсечных сочетания, каждое из которых включает по семь событий: 1·2·3·4·5·12·13, 1·2·3·4·6·12·13, 7·8·9·10·11·12 и 13.

Приведенные результаты предварительного качественного анализа процесса возникновения конкретного происшествия позволяют оценить условия его появления и предупреждения. Наиболее критичными и значимыми (в указанном смысле) предпосылками являются те исходные отказы, которые связаны с невозможностью своевременного отключения насоса, а также не учитываемое моделью возможное разрушение стенок бака, а наименьшую – отказы таких элементов, как расходомер и датчик уровня.

Не приводя дополнительных соображений по этому поводу, заметим лишь, что мера значимости или критичности конкретной предпосылки обратно пропорциональна количеству смежных с ней других событий в минимальном пропускном сочетании и – пропорциональна числу содержащих её минимальных отсечных сочетаний. Подчеркнем, что все они образованы из постулируемых исходных предпосылок. Следовательно, можно утверждать: из рассматриваемых событий нижнего уровня наиболее критичны – под номерами 12 и 13, а наименее значимы – 5 и 6; остальные исходные предпосылки качественно равнозначны как по влиянию на условия возникновения пожара, так и на условия его предупреждения.

Более точные результаты могут быть получены при количественном анализе дерева происшествий.