Качественный и численный анализ космологической модели, основанной на фантомном скалярном поле с самодействием. II. Сравнительный анализ моделей с классическим и фантомным полями

С формальной точки зрения фантомные поля были введены в гравитацию в качестве одной из возможных моделей скалярного поля в 1983 году в работе одного из Авторов [1]. В указанной работе, а также и в более поздних (см., например, [2], [3]) фантомные поля классифицировались как скалярные поля с притяжением одноименно заряженных частиц и выделялись множителем е = - 1 в тензоре энергии - импульса скалярного поля⁴. В последующих работах, начиная с 2012 года, неминимальная теория скалярного взаимодействия на основе понятия фундаментального скалярного заряда последовательно развивалась, как для классических, так и фантомных скалярных полей [6], [7], [8], [9]. В частности, в этих работах были выявлены некоторые особенности фантомных полей, в частности, особенности межчастичного взаимодействия. С 2014 [10], [11], [11], [12], [13], [14] эти исследования были углублены для распространения теории скалярных, в том числе, и фантомных полей на сектор отрицательных масс частиц, вырожденные Ферми-системы, конформно-инвариантные взаимодействия и тому подобное. С 2015 года сконструированные математические модели скалярных полей были применены к исследованию космологической эволюции систем взаимодействующих частиц и скалярных полей, как классического, так и фантомного типов [15], [16], [17]. Эти исследования выявили уникальные особенности космологической эволюции плазмы с межчастичным фантомным скалярным взаимодействием, такие как существование гигантских всплесков космологического ускорения, наличие плато с постоянным ускорением и тому подобное.

Однако, построенные численные модели не могут полностью удовлетворить физика - теоретика, так как не дают возможности аналитического описания этих явлений и выявления природы обнаруженных особенностей. В связи с этим возникает необходимость качественного исследования космологических моделей, основанных на скалярном взаимодействии. В качестве первого шага необходимо провести качественное исследование космологических моделей, основанных на свободных скалярных полях. Такие исследования для классического скалярного массивного поля проводились с 1985 года [18], [19], [22], [20], [24] (см. также [21]). В работе Журавлева [20] методами качественной теории динамических систем исследовалась также двухкомпонентная космологическая модель с минимальным взаимодействием. В статье одного из Авторов [25] была показана некорректность так называемого приближения «медленного скатывания» и заново проведен качественный, а также и численный анализ космологической стандартной космологической модели, основанной на классическом скалярном поле, сведением задачи к исследованию динамической системы на плоскости. При этом был показан микроскопический колебательный характер инвариантного космологического ускорения на поздних стадиях расширения. Далее результаты были обобщены на космологические модели с Λ - членом [26], [29], причем удалось подтвердить сохранение колебательного характера инвариантного космологического ускорения при достаточно малых значениях величины космологического члена. В работе В.М. Журавлева [28] был использован метод исследования, предложенный в указанных работах, и применен к двухкомпонентной системе «скалярное поле+жидкость» с произвольной потенциальной функцией V(ф)5. К некоторым результатам этой работы мы еще вернемся ниже.

Далее, в работах [30], [31] и [32] был частично проведен качественный анализ космологической модели, основанной на фантомном скалярном поле с самодействием. В настоящей работе мы разовьем и детализируем результаты исследований космологических моделей, основанных на классическом и фантомном скалярных полях.

L = 8 П д ^ ^кк Ф ’ i Ф ’ к — е 2 m ²Ф² + а Ф ⁴) ’

(1.1)

где α - константа самодействия; для поля с отталкиванием одноименно заряженных частиц е ₁ = 1, для поля с притяжением одноименно заряженных частиц е ₁ = — 1; для классического скалярного поля е ₂ = 1, для фантомного скалярного поля е ₂ = — 1. Заметим, что одиночное классическое скалярное поле с притяжением одноименно заряженных частиц существовать не может, так его энергия строго отрицательна. Тензор энергии - импульса относительно функции Лагранжа (1.1) равен

T^lk = еП ^ 2Ф ’ ¹ Ф ’ ^к — g^lk Ф ’ j Ф ’ j + g^ikе ₂ m ²Ф² — g^ikа ф⁴ ) .

(1.2)

Для приведения к обозначениям, стандартным для космологических моделей со скалярными полями, перепишем функцию Лагранжа (1.1) в другой нормировке, учитывая тот факт, что к функции Лагранжа можно добавить произвольную константу:

L = 8 П (^Ф - i Ф ' к - ² V (Ф))’

(1.3)

(1.4)

где

1                      а m ^{2 2}

V (Ф) = — -( а Ф⁴ — 2 е ₂ m ²Ф²) ^ — - Ф² — е ₂- ^ •

Очевидно, что в уравнениях Эйнштейна такая перенормировка потенциала будет эквивалентна перенормировке космологической постоянной

4 m ⁴

(1.5)

Л = Л о — е 1—— ;  ( а ^ 0),

2а где Ло - некоторое «затравочное» значение космологической постоянной. Таким образом, в терминах Лагранжиана (1.3), потенциальной энергии (1.4) рассматриваемая потенциальная функция в работах [30], [31] эквивалентна Хиггсовому потенциалу (1.4). В терминах этих величин модель полностью определяется знаками е1, е2 и а.

Тензор энергии-импульса скалярного поля в терминах этих величин принимает стандартный вид:

T ik = I ¹ ( 2Ф ’ i Ф к — g ik Ф ^ Ф ^ ' + 2 V (Ф) g ik ) .

8 П

(1.6)

Равенство нулю ковариантной дивергенции этого тензора приводит к уравнению свободного скалярного поля:

• □Ф + V '(Ф) = 0.(1.7)

В частности, при использовании функции потенциальной энергии в форме (1.4) получим из (1.7):

• □Ф + m 2 Ф = 0,(1.8)

где m * - эффективная масса скалярного бозона

m* = е2m2 - аФ2,(1.9)

которая может быть и мнимой величиной.

Выпишем также уравнения Эйнштейна с космологическим членом Л >  0 ⁶

R ik — 2 Rg^ik = Л g^ik + 8 nT^ik ,                             (1.10)

где необходимо учитывать связь между «затравочным» значением космологической постоянной и ее эффективным значением (1.5).

1.2.Самосогласованныеуравнениядляпространственно-плоскоймоделиФридмана

Выпишем самосогласованные уравнения пространственно - плоской космологической модели ds2 = dt2 - a2(t)(dx2 + dy2 + dz2)                          (1.11)

• -    уравнение Эйнштейна

3 aL = е i ( Ф² + е 2 m ²Ф² - ⁰ Ф⁴ ) + Л                         (1.12)

и уравнение массивного скалярного поля с кубической нелинейностью7:

Ф + 3 a Ф + е 2 m 2 Ф = 0.                             (1.13)

При этом тензор энергии - импульса (1.2) имеет структуру тензора энергии - импульса изотропной жидкости с плотностью энергии и давлением:

е = — ( Ф² + е₂ m ² Ф ² - ⁰ Ф⁴ ) ;

8 nV      ²         2

p = 8L ( ф² - е ₂ m ²Ф² + О. ф ⁴ ) ,                               (1.14)

так что:

_ е 1 <Ф²

^{Е +} p = 4 п ‘

1.3.Кинематическиеинварианты

В дальнейшем нам также понадобятся значения двух кинематических инвариантов Вселенной Фридмана:

й          ай     H 1

H ( t ) = - > 0; Q( t ) =    = 1 +                                 (1.15)

a           a²      H ²

• -    постоянная Хаббла и инвариантное космологическое ускорение.

• 2. Качественный анализ

2.1.Приведениесистемыуравненийкнормальномувиду

Пользуясь тем, что постоянную Хаббла можно выразить из уравнения Эйнштейна (1.12) через функции Ф, Ф, переходя к безразмерному комптоновскому времени:

mt = т ; ( m ^ 0)

и проводя стандартную замену переменных Ф' = Z(t), приведем уравнение поля (1.13) к виду нормальной автономной системы обыкновенных дифференциальных уравнений на плоско сти {Ф, Z}:

Ф ‘ = Z ;

• Z' = -V3 У € 1 (Z2 + € 2Ф2 - am Ф4) + Л m Z — € 2 Ф + «ш Ф3,(2.1)

где f ‘ = df I dт и введены обозначения:

Лm = Г; am =9"

m2

При этом:

а ‘             аа"h

H = m— = mh; Q = —— = 1 + —•

Таким образом, имеем автономную двумерную динамическую систему на фазовой плоскости {Ф, Z }. Для приведения её к стандартным обозначениям качественной теории дифференциальных уравнений (см., например, [15]) положим:

Ф = x ; Z = у ;

• p ( x , у ) = у ;

2.2.Особыеточкидинамическойсистемы

Q (x, у) = -VS У € 1 (у2 + € 2 X2 - amx4) + Л m у - € 2 X + «mX3.(2.3)

Соответствующая нормальная система уравнений в стандартных обозначениях имеет вид:

x' = P(x,у); у' = Q(x,у).(2.4)

Для того, чтобы система дифференциальных уравнений (2.1) (или (14)) имела вещественное решение, необходимо выполнение неравенства:

€ 1 (у2 + €2x2 - amx4j + Лm > 0.(2.5)

Особые точки динамической системы определяются уравнениями (см., например, [15]) :

M: P(x, у) = 0; Q(x, у) = 0.(2.6)

Очевидно, что при любых значениях am и Лm > 0 система алгебраических уравнений (2.5), как и в работах [13]-[14] имеет одно тривиальное решение x = 0;у = 0 ^ M0(0,0).(2.7)

Кроме того, в случае одноименных знаков € ₂ и a m , возможны и нетривиальные симметричные решения:

x = x± = + ,     ;у = 0 ^ M±(x±,0).(2.8)

• V^€ 2 ^a m

2.3.Характеристическоеуравнениеикачественныйанализвслучаевблизинулевойособой точки

Подставляя решения (2.8) в условие (2.5), получим необходимое условие вещественности решений в особых точках (2.7) и (2.8):

ǫ

(17) - Л m >  0; (18) - Л m + — >  0.                      (2.9)

Вычислим производные функций (2.3) в нулевой особой точке (2.6) при Л m >  0 :

Таким образом, получаем характеристическое уравнение и его корни (см. [15]):

— Л       1

= 0

^

^- € 2 ^{— Л —} V ^ЗЛ m

Л ± =

—

3Λ _m

±

3Λ _m

—

4 ǫ ₂

.

(2.11)

∂P		∂P
—	= 0;	—	= 1;
dx ∂Q ∂x	M 0 = — € 2 ; M 0	∂y ∂P ∂y	M 0 = — V ЗЛ m . M 0	(2.10)

• 2.4.    Численное интегрирование модели без космологическойпостоянной ( Л = 0 )с классическим скалярным полем (с ₁ = 1 , € ₂ = 1 ) без самодействия (а = 0 )

В этом случае корни характеристического уравнения (2.9) принимают значения:

Л = ± i .

(2.12)

Поскольку собственные числа оказались чисто мнимыми, то единственная особая точка (2.7) динамической системы является центром (см. [26]). В этом случае при т — +го фазовая траектория динамической системы наматывается на этот центр, совершая бесконечное множество витков.

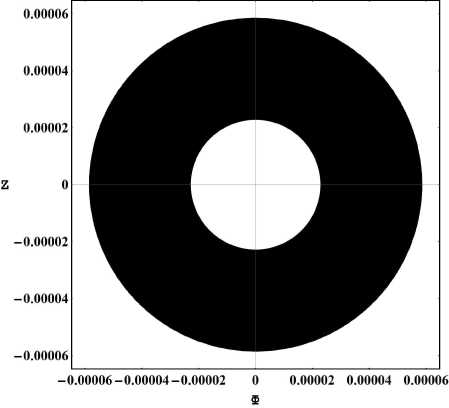
Рис. 1. Фазовый портрет системы (2.1) в крупном масштабе для случая a m = 0; Л m = 0;

Ф(0) = 100; Z (0) = 0; т = 20000 ^ 50000.

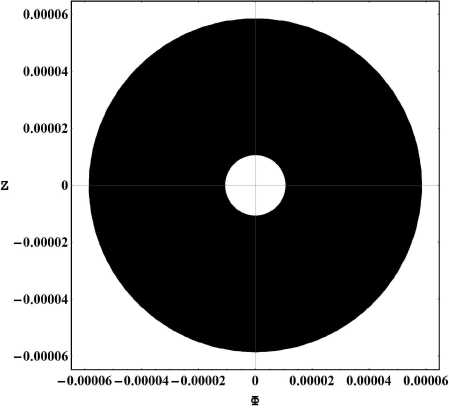
Рис. 2. Тот же случай т = 20000 ^ 105000.

• 2.5.    Численное интегрирование модели с космологической постоянной ( Л >  0 )с классическим скалярным полем (с ₁ = 1 , с ₂ = 1 ) без самодействия (a m — 0 )

В этом случае корни характеристического уравнения (2.9) принимают значения:

. _ v^ VЗЛ m - 4

(2.13)

А+ —-- ±--------

±        2         2

Возможны случаи [31]:

• 1)    Л m <  4/3 — собственные значения комплексно сопряженные с отрицательными действительными частями — притягивающий фокус.

• 2)    Л m >  4/3 — собственные значения действительные разные отрицательные — устойчивый узел.

Можно показать, что характер особой точки не меняется при учете второго порядка теории возмущений, так как все вторые частные производные динамической системы в центральной точке равны нулю:

(2.14)

M 0

∂ ² P ∂x ²

д2 P      д2 P дхд У M.о   д У2 Mо

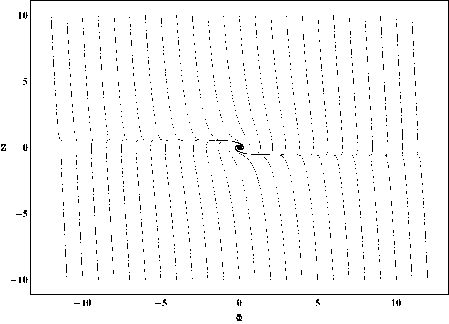
Рис. 3. Фазовый портрет системы (2.1) в крупном масштабе для случая a m — 0;

Л _m — 0.0001; т — 0 * 90.

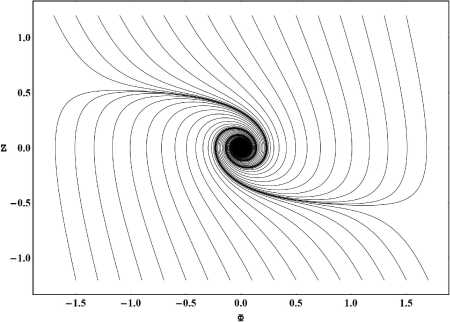
Рис. 4. Тот же случай, окрестности особой точки.

• 2.6.    Численное интегрирование модели с космологической постоянной ( Л >  0 )с фантомным ска -лярным полем (с ₁ — - 1 , с ₂ — - 1 ) без самодействия (a m — 0 )

В этом случае корни характеристического уравнения (2.9) принимают значения:

. _  х/зд т  V ЗЛ m + 4

(2.15)

А+ —-- ±--------

±        2         2

При любых Λ m корни характеристического уравнения действительные разных знаков — особая точка седло.

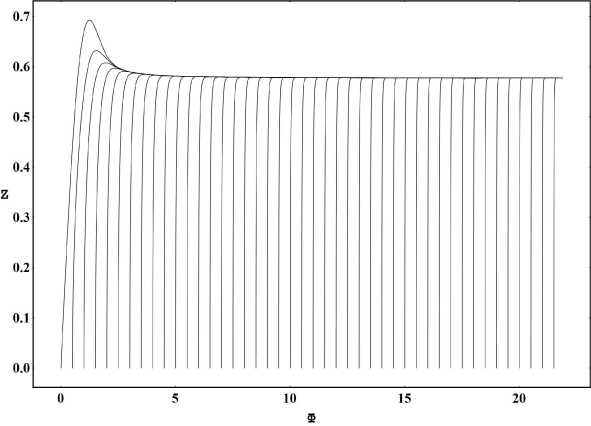
Рис. 5. Фазовый портрет системы (2.1) для случая a m — 0; Л m — 0.0001; т — 0 * 30.

• 2.7.    Численное интегрирование модели с космологической постоянной ( Л >  0 ) с фантомным ска -лярным полем (с ₁ = — 1 , с ₂ — — 1 )с самодействием (a m <  0 )

В этом случае корни для центральной точки вновь имеем седло:

. _ V3A m  V ЗЛ m + 4

X+ —-- ±--------

±        2         2

Производные функций (2.3) в особых точках (2.8) при Л _m >  0 равны:

∂P		— 0; M ±	∂P	___1.
∂x			∂y	= 1; M ±
∂Q ∂x	— — 2; M ±		∂P ∂y	—— M ±	1 /3 Л m — -    . 2 α m

Характеристические уравнения для обеих особых точек совпадают и собственные точки имеют один тип (см. [15]):

— X

— X —

г /    ~ v3УЛ m—2am

— о

^

X ±

А ^Л m ^— ~-

2 α _m

±

Λ _m

2 α m 3

(2.16)

Вследствие (2.9) подкоренное выражение в первом члене (2.16) строго больше нуля, поэтому возможны три случая:

• 1)    Л _m — 1/2 a m — 8/3 >  0 - тогда оба собственных значения вещественны и отрицательны. В этом случае решение содержит два симметричных притягивающих (устойчивых) невырожденных узла . Все фазовые траектории в окрестности таких особых точек при t -^ го входят в эти точки и кроме двух исключительных касаются собственного вектора минимальной длины.

• 2)    Л _m — 1/2 a m — 8/3 — 0 - тогда оба собственных значения отрицательны и равны. В этом случае решение содержит два симметричных вырожденных узла .

• 3)    Л _m — 1/2 a m — 8/3 <  0 - тогда оба собственных значения комплексно сопряженные, причем их действительные части отрицательны. В этом случае решение содержит два симметричных притягивающих фокуса .

В случае двух симметричных фокусов легко найти предельное значение h _го , к которому стремится постоянная Хаббла при t ^ го . Подставив координаты фокусов M ± ( ±-^= ,0) в систему

(2.1), получим:

h ” = ylFTi a j •

(2.17)

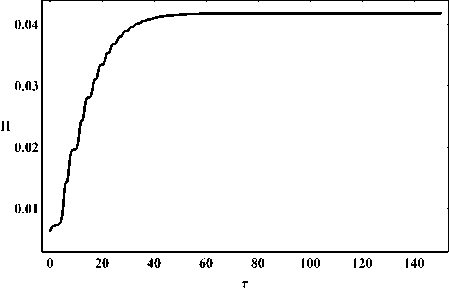
Рис. 6. Эволюция приведенного постоянной Хаббла для случая a m = - 100; Л m = 0.00001; Ф(0) = 0.4; Z (0) = - 0.4; т = 0 * 150.

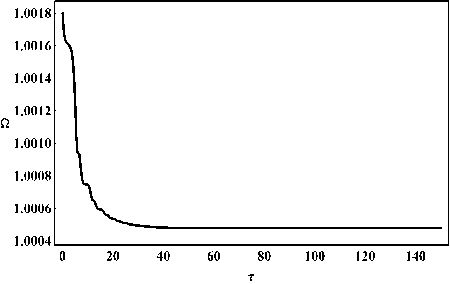
Рис. 7. Эволюция космологического ускорения для того же случая.

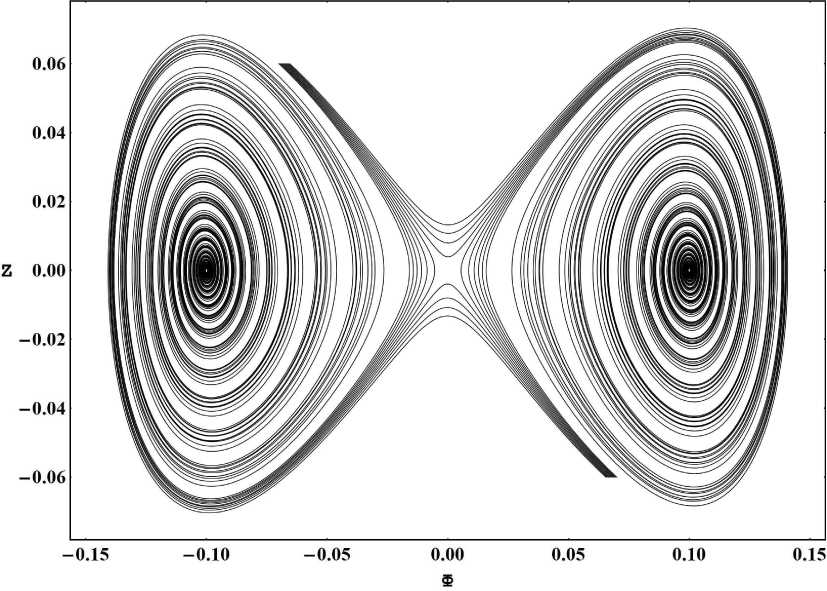
Рис. 8. Фазовый портрет системы (2.1) в крупном масштабе для случая a m = - 100; Л m = 0.00001; {Ф(0) = - 0.07 + ( j - 1) * .0005, j = 1..10; Z 0 = 0.06}, {Ф(0) = 0.07 + ( j - 1) * .0005, j = 1..10; Z 0 = - 0.06}; т = 0 ^ 90.

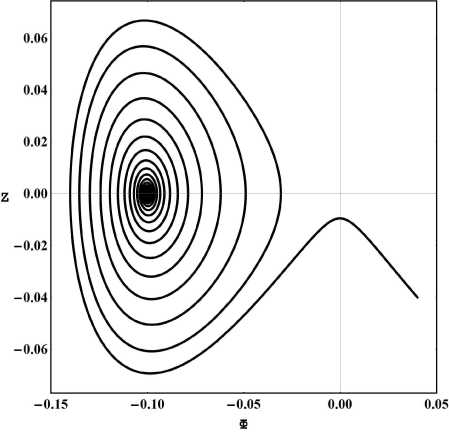
Рис. 9. Фазовый портрет системы для того же случая, оси Φ, Z .

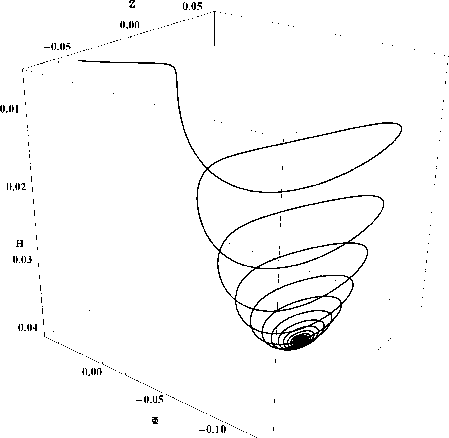
Рис. 10. Фазовый портрет системы для того же случая, оси Φ, Z , h .

На рисунках 11 - 16 приведены результаты численного моделирования эволюции решения системы в зависимости от космологической постоянной: с ₁ = - 1, с ₂ = - 1, a m = - 1, Л m = {0,0.01,0.1}, Z (0) = 0, Ф(0) = 0.1, т = 0 * 50.

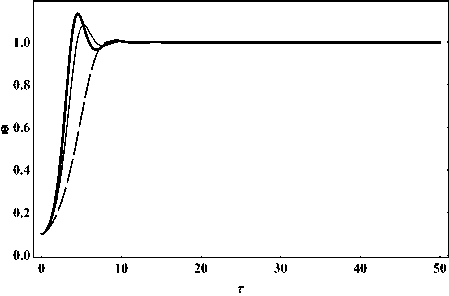
Рис. 11. Эволюция потенциала скалярного

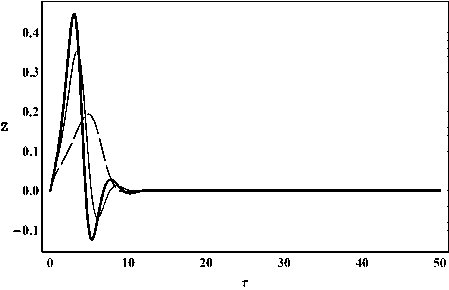
Рис. 12. Эволюция производной потенциала скалярного поля Z = Ф.

поля Ф для случая a m = - 1; Z (0) = 0; т = 0 ^ 50; Л _m = 0 - жирная линия, Л _m = 0.01 - тонкая линия, Л _m = 0.1 - пунктирная линия.

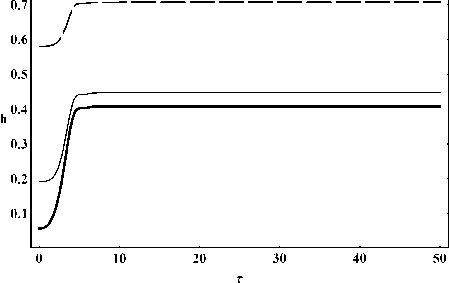
Рис. 13. Эволюция постоянной Хаббла.

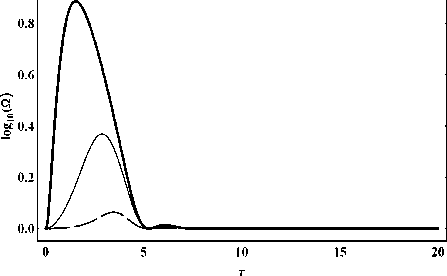
Рис. 14. Эволюция логарифма космологического ускорения.

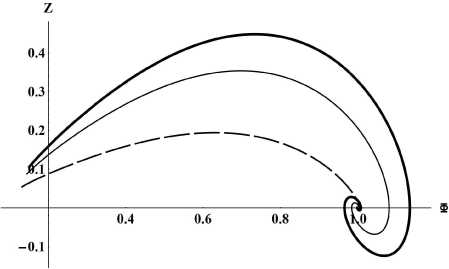
Рис. 15. Фазовый портрет системы.

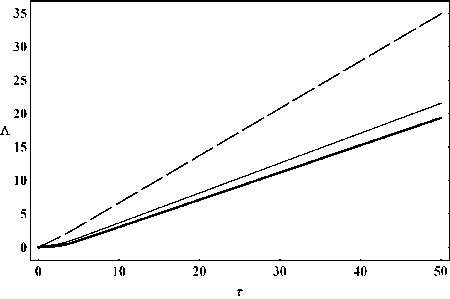
Рис. 16. Эволюция функции масштабного фактора Л = In a .

• 2.8.    Численное интегрирование модели без космологической постоянной ( Л = 0 )с фантомным скалярным полем (с ₁ = - 1 , с ₂ = - 1 )с самодействием (a m <  0 )

На рисунках 17 - 20 приведены результаты численного моделирования системы для случая: с 1 = - 1, с 2 = - 1, a m = - 10, Л m = 0, Z (0) = - 0.4, Ф(0) = {0.1,0.05,0.01}, т = 0 - 50.

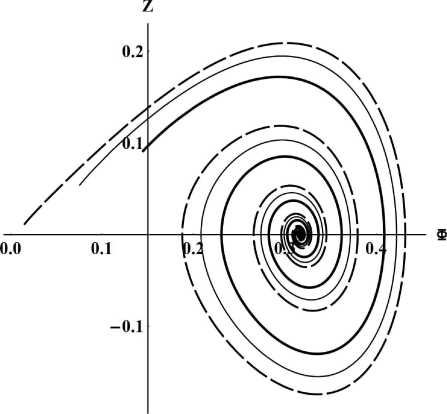
Рис. 17. Фазовый портрет системы для случая a _m = - 10; Л m = 0; Z (0) = - 0.4; т = 0 - 50; Ф(0) = 0.1 - жирная линия, Ф(0) = 0.05 - тонкая линия, Ф(0) = 0.01 - пунктирная линия.

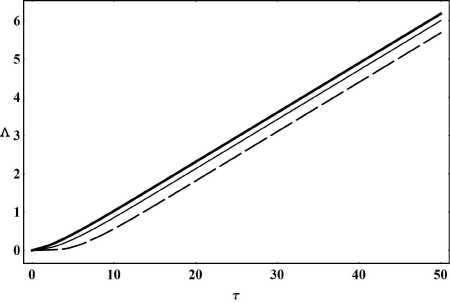
Рис. 18. Эволюция функции масштабного фактора Л = In a .

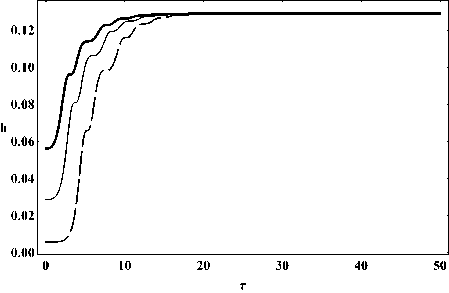
Рис. 19. Эволюция постоянной Хаббла.

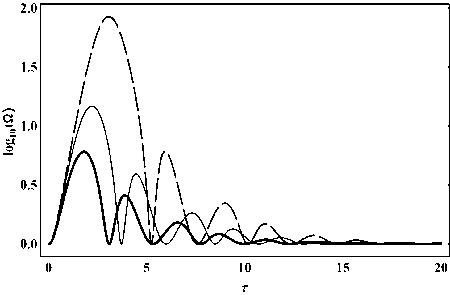
Рис. 20. Эволюция логарифма космологиче- ского ускорения.

На рисунках 21 - 25 приведены результаты численного моделирования эволюции системы в зависимости от константы самодействия: е ₁ = - 1, е ₂ = - 1, a m = { - 1, - 10, - 50}, Л m = О, Z (0) = О, Ф(0) = 0.1, т = 0 ^ 50.

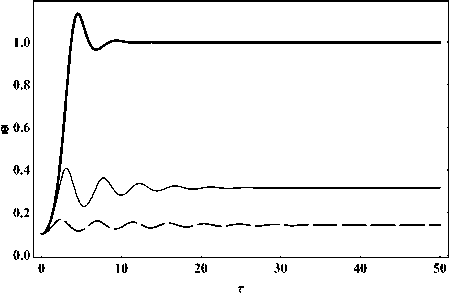
Рис. 21. Эволюция потенциала скалярного поля Ф для случая Л m = 0; Z (0) = 0; т = 0 ^ 50; Ф(0) = 0.1; a m = - 1 - жирная линия, a m = - 10 - тонкая линия, a m = - 50 - пунктирная линия.

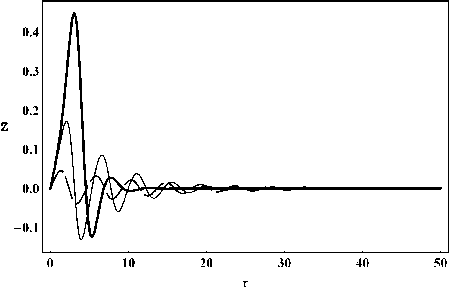
Рис. 22. Эволюция производной потенциала скалярного поля Z = Ф.

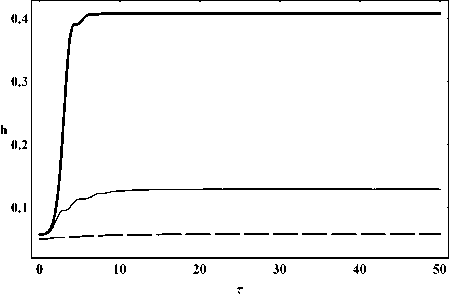
Рис. 23. Эволюция постоянной Хаббла.

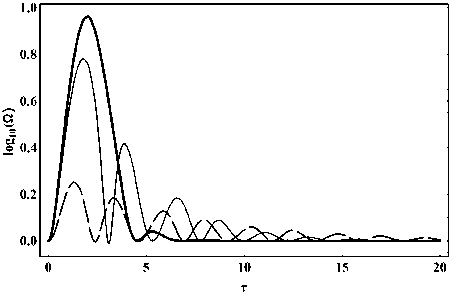
Рис. 24. Эволюция логарифма космологического ускорения.

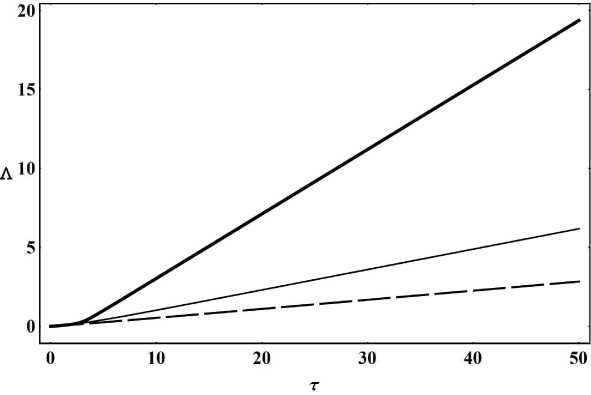
Рис. 25. Эволюция логарифма масштабного фактора Л = In a .

2.9.ЧисленноеинтегрированиемоделисклассическимскалярнымполемсХиггсовскимпотен-циаломсамодействия.

Рассмотрим классическое скалярное поле с потенциалом самодействия Хиггса:

V ^{( ф )} = 2 (^{ф2 -} 3 ²"

Таким образом, система (2.1) перепишется как:

Ф ‘ = Z ;

Z' = -V5 Z\U2 + am Ф4 - втФ2 + ^1+ Л m - am Ф3 + РтФ, 2            2αm где:

^Л т ^—    ₉ ^;

m ²

a m — ^a ; m ²

Рт ^— "^*

m ²

Особые точки системы:

M 0 (0,0),

M ±|± ил

(2.18)

(2.19)

На рисунках 26 - 28 приведены результаты численного моделирования системы для случая: е i = 1, a m = 1, Р т = 0.5, Л т = 0.000001, Z (0) = - 0.1, Ф(0) = 1, т = 0 - 10000.

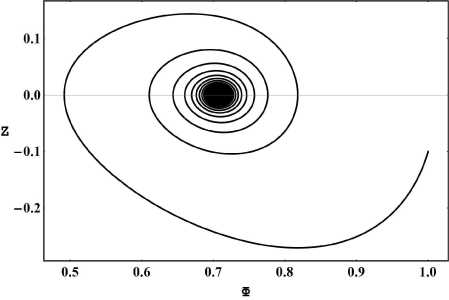
Рис. 26. Фазовый портрет системы с Хигг-совским потенциалом самодействия т = 0 ^ 1000.

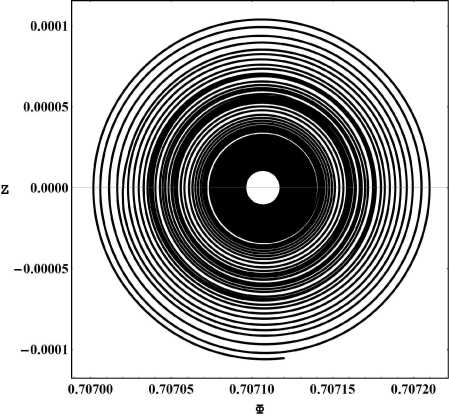
Рис. 27. Фазовый портрет системы с Хигг-совским потенциалом самодействия в крупном масштабе: е ₁ = 1; а _т = 1; р _т = 0.5; Л _т = 0.000001; Z (0) = - 0.1; Ф(0) = 1; т = 1000 ^ 10000.

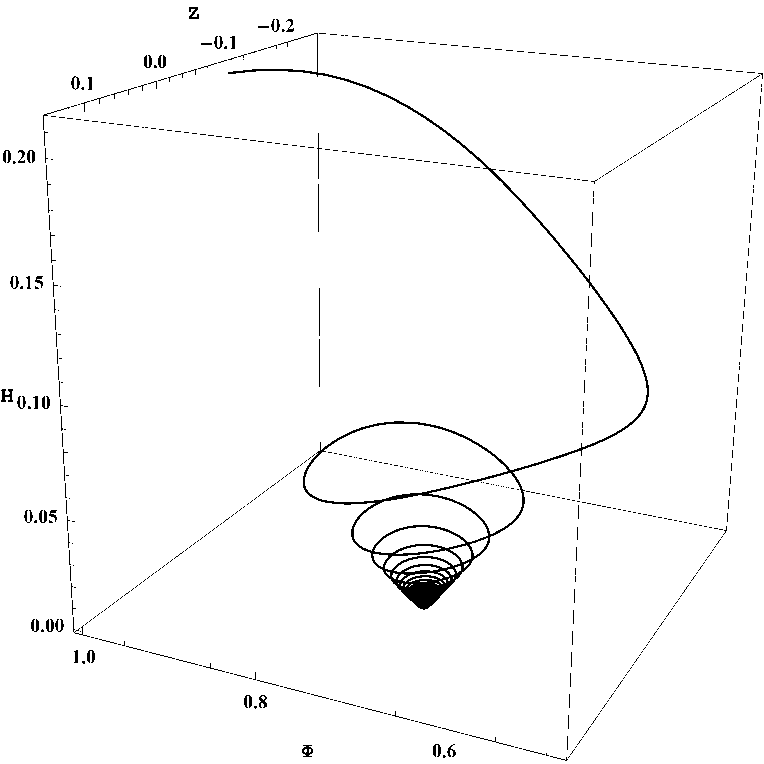
Рис. 28. Трехмерный фазовый портрет системы для того же случая; оси Φ, Z , h .

С другой стороны, полагая при т -^ m Ф( т ) ^ О, Z ( т ) ^ 0 и пренебрегая квадратами этих членов в уравнениях (2.1) по сравнению с Λ _m , приведем последние в случае классического скалярного поля к виду:

ф" + V зл m ф ' +ф = о. (3.1)

Решение этого уравнения

Ф = е ^- V^ ^т (с ₊ е ⁺ i^ ^{1 -} 4 ^л m ^т + C - е ^- iV ^{1 -} 4 ^Л m ^т );

^(Л m <  3 ⁾

(3.2)

описывает затухающие колебания с характерным временем затухания т _e ff =

^ЗЛ m

. В моде-

лях без космологического члена (Л = 0) уравнение (3.1) описывает незатухающие колебания, и

решение содержит центр [25].

Во-вторых, колебания системы вблизи особой точки происходят с периодом порядка:

T =

2 п

V1 - 4 Л m

~ 2 п ,

(3.3)

то есть, с комптоновским по отношению к массе скалярных бозонов периоду. Это, как отмечалось в [26] - микроскопические времена, недоступные классическим измерениям. Поэтому о наблюдаемых колебаниях масштабных функций ( a ( t ), H ( t ), Q( t )) на современном этапе космологической эволюции говорить неправомерно. Речь идет, скорее всего, о продолжающихся затухающих квантовых осцилляций скалярного поля, которые должны восприниматься как рождение Хиггсовых бозонов, вероятность которого уменьшается экспоненциально быстро со временем.

Заметим также, что динамические уравнения (2.1) сводятся к обыкновенному дифференциальному уравнению вида:

x + в ( x , ^ x ) x c - V’ _x ( x ) = 0,                                       (3.4)

где x (t) = ф (т), в (x, -x) =

2 e i ( 2 x ² - V ( x ) ] + Л m >  0.

(3.5)

Таким образом, уравнение (3.4) по своей физической сути представляет уравнение одномерных колебаний в поле Хиггсова потенциала V ( x ) с неотрицательным коэффициентом нелинейного трения в ( x , x ) Вне зависимости от явного вида коэффициента трения суть процесса, описываемого уравнением (3.4), физически прозрачна — это затухающие колебания в потенциальной яме V ( x ). В случае Хиггсова потенциала система опускается в один из устойчивых минимумов V ( x ) (Рис. 29). Таким образом, при Ф ^ О, Z ^ 0 и Л >  0 коэффициент трения постоянен. В случае а = 0 потенциал V ( x ) имеет форму параболы, поэтому система обязана опускаться в ее вершину. В случае Л = 0 при Ф ^ О, Z ^ 0 коэффициент трения стремится к нулю, поэтому только в этом случае и возможны незатухающие колебания при т ^ то .

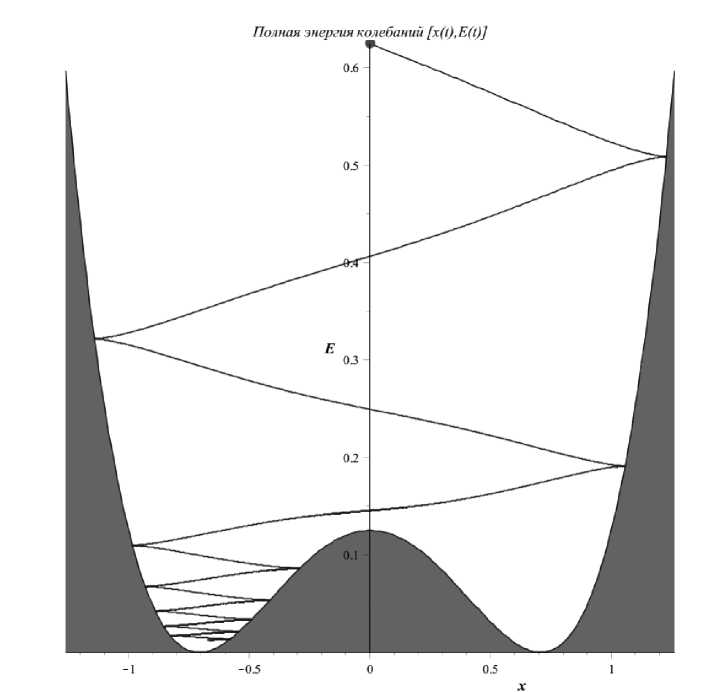
Рис. 29. Компьютерная симуляция затухающих колебаний в поле потенциала Хиггса [35].

Что же касается численных результатов и следующих из них выводов статьи, касающихся существования предельного цикла космологической динамической системы в случае Л ^ 0, как видно из рисунков 30 и 31, для получения более точных результатов на больших временах эволюции необходимо применять более точные методы интегрирования нелинейных уравнений.

Из сравнения графиков на рисунках 30 и 31 видно, что метод интегрирования Рунге - Куд-та 4-5 порядков при больших значениях времени эволюции динамической системы и малых значениях потенциала скалярного поля и его производной приводит к существенным ошибкам. Представленная на рисунке 30 фазовая диаграмма весьма интересна, но не соответствует действительности. На рисунке 31 мы видим правильную фазовую диаграмму, полученную для этого же случая методом интегрирования Рунге - Кудта повышенной точности 7-8 порядков. Эта диаграмма как раз и описывает затухающие колебания (3.2). Обращаем внимание на поразительную точность вычислений с помощью метода Рунге - Кудта 7-8 порядков: радиус спирали на исследуемом этапе составляет порядка 10 ^{- 192}! Обращаем также внимание и на то обстоятельство, что фазовая диаграмма на рисунке 30, полученная методом Рунге - Кудта 4-5 порядков при этом дает значения потенциала и его производной, завышенные на 184 порядка!

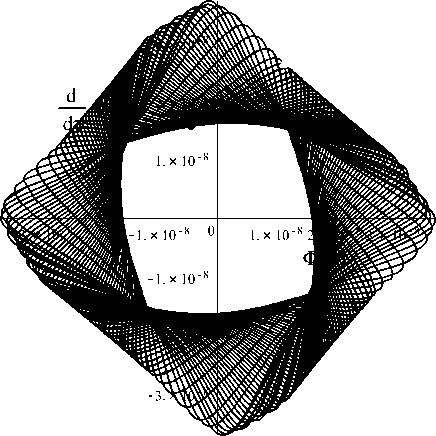
Рис. 30. Фазовый портрет системы (2.1) в крупном масштабе для случая a m = 0; Л m = 0.001; т = 9000 * 10000; Ф(0) = 1; Z (0) = 0. График получен с помощью стандартного метода Рунге - Кудта 4-5 порядков в пакете Maple 18.

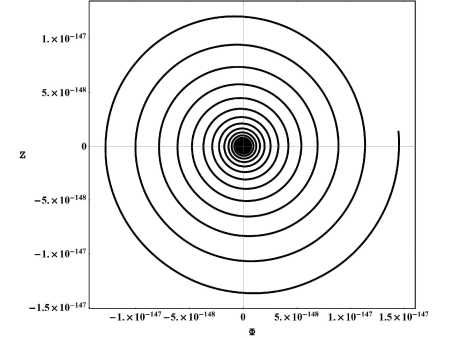
Рис. 31. Фазовый портрет системы (2.1) в крупном масштабе для случая a m = 0; Л m = 0.001; т = 9000 ^ 10000; Ф(0) = 1; Z (0) = 0. График получен с помощью метода интегрирования высокой точности Рунге - Кудта 7-8 порядков в пакете Maple 18.

На рисунках 32 — 35 показаны фазовые диаграммы динамической системы на больших временах в случае нулевого значения космологической постоянной. Как видно из представленных фазовых диаграмм, в случае Л = 0, действительно, фазовые диаграммы очень похожи на предельные циклы, причем с практически строго круговой орбитой в наших переменных. Однако, можно заметить и неуклонную тенденцию к уменьшению радиуса этих циклов с увеличением времени эволюции динамической системы.

Тенденция же эволюции фазовых диаграмм такова, что

Ф²( т ) + Ф ' ²( т ) = Ф 0 ( т ) « const; ( т » 1),                           (3.6)

причем до определенного момента времени выполняется приближенное соотношение Φ 0 ( τ ) ∝ т ^{- 5/2} - медленно меняющаяся функция по сравнению с фазой колебаний; после чего Ф ₀ ( т ) падает гораздо быстрее.

Общую тенденцию падения амплитуды колебаний в случае Л = 0, a = 0 можно понять и на основе анализа уравнения поля

Ф" + ^ЗФ' у/ф2 + Ф'2 + Ф = о(3.7)

при учете свойства (3.6). Действительно, учитывая (3.6) и полагая в (3.7)

Ф = Фо( т )е iт, получим:

Ф0 + 2 i ФО + х ЗФО Фо + i VЗФO = 0.(3.8)

Учитывая Ф О « Ф _о , получим в первом приближении из (3.8) закон эволюции амплитуды:

Φ0∝     ,(3.9)

3τ что подтверждает вывод о падении амплитуды колебаний с течением времени.

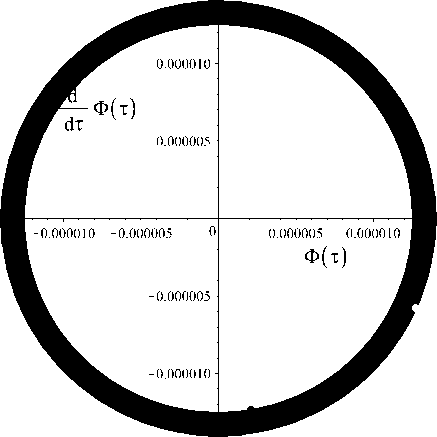
Рис. 32. Фазовый портрет системы (2.1) в крупном масштабе для случая a m = 0; Л m = 0; т = 9000 ^ 10000; Ф(0) = 1; Z (0) = 0. График получен с помощью стандартного метода Рунге - Кудта 4-5 порядков в пакете Maple 18.

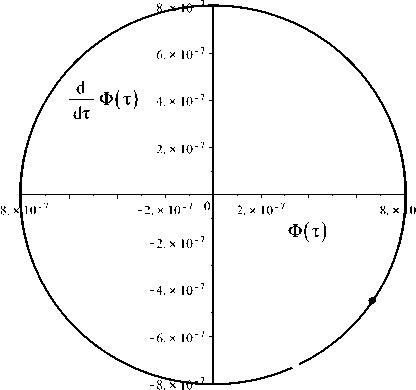
Рис. 33. Фазовый портрет системы (2.1) в крупном масштабе для случая a m = 0; Л m = 0; т = 100000 ^ 100100; Ф(0) = 1; Z (0) = 0. График получен с помощью метода интегрирования высокой точности Рунге - Кудта 7-8 порядков в пакете Maple 18.

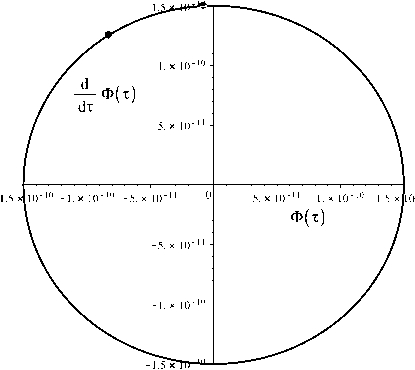
Рис. 34. Фазовый портрет системы (2.1) в крупном масштабе для случая a m = 0; Л m = 0; т = 1000000 ^ 1000100; Ф(0) = 1; Z (0) = 0. График получен с помощью стандартного метода Рунге - Кудта 4-5 порядков в пакете Maple 18.

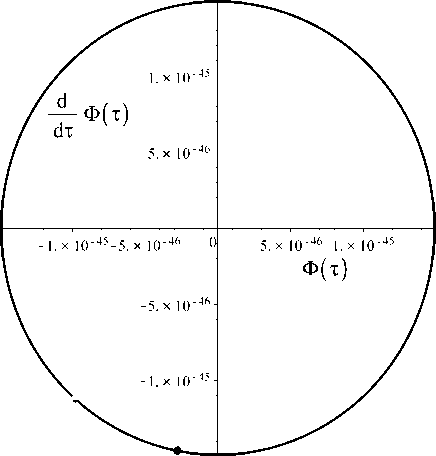
Рис. 35. Фазовый портрет системы (2.1) в крупном масштабе для случая a m = 0; Л m = 0; т = 10000000 ^ 10000100; Ф(0) = 1; Z (0) = 0. График получен с помощью метода интегрирования высокой точности Рунге - Кудта 7-8 порядков в пакете Maple 18.

Заключение

В заключении Авторы выражают благодарность членам ВС (MW) — семинара по релятивистской кинетике и космологии Казанского федерального университета за полезное обсуждение работы.