Как использовать результаты кадастровой оценки в оценочной практике

С введением института кадастровой оценки в Российской Федерации постоянно возникают споры (досудебные и судебные), подвергающие сомнению результаты кадастровой оценки. Поскольку предполагается регулярный пересмотр кадастровой стоимости, такие споры обещают войти в постоянную практику действующих оценочных компаний. Это совершенно естественно, так как отношения налогоплательщик – государство в узком (микроэкономическом) смысле являются простейшей игрой с нулевой суммой. Один игрок заинтересован в увеличении «выигрыша», второй – в уменьшении «проигрыша». В этих условиях оценочным компаниям приходится решать вопрос о целесообразности оспаривания кадастровой стоимости, так как отчет об оценке является платной услугой, а «выигрыш» для заказчика в виде снижения налогового бремени необязательно соответствует затратам, понесенным на оценку, и часто невозможен в принципе (с точки зрения перспективы выигрыша арбитражного дела).

Первоначальной целью настоящей статьи было желание разобраться, как изменилась кадастровая стоимость с 1 января 2015 по 1 января 2018 года, и определить, в каких случаях имеются достаточные основания для пересмотра кадастровой стоимости. В процессе исследования получены два результата, которые могли бы представлять интерес для повседневной практики оценки:

• 1)    возможность оценки темпов роста секторов рынка и ее использование в рамках доходного подхода;

• 2)    возможность расчета корректировок по ценообразующим факторам при применении сравнительного подхода.

Сравнивались результаты кадастровой оценки, проведенной в 2015 и 2018 годах, опубликованные Санкт-Петербургским государственным унитарным предприятием «Городское управление инвентаризации и оценки недвижимости» (далее – ГУП ГУИОН») в 2015 году [1] и Санкт-Петербургским ГУ «Кадастровая оценка» в 2018 году [2]. Пара удельных кадастровых стоимостей (кадастровая стоимость одного квадратного метра жилой недвижимости) в 2015 и 2018 годах (далее – КС2015 и КС2018 соответственно) рассматривается как двумерная случайная величина 1. Аналогичное сравнение для рыночных стоимостей имеет очевидное препятствие: в рыночных базах данных нет кадастрового номера, который позволяет точно идентифицировать объект. В статье [3] показано, как можно обойти это препятствие сравнением рыночных данных с кадастровыми базами.

Приведенные далее результаты исследования в основном базируются на стохастической модели ценообразования, подразумевающей совместную нормальность логарифмов цен. Теоретические основания для такой модели были опубликованы в статьях [4, 5]. Такой подход применен к двумерному совместному распределению случайных величин КС₂₀₁₅, КС₂₀₁₈, которые в формулах будут обозначаться V ₂₀₁₅, V ₂₀₁₈. Его применение к кадастровым стоимостям представляется оправданным по следующим причинам:

• 1)    база кадастровых стоимостей рассматривается как выборка (см. сноску 1) объектов, прошедших кадастровый учет два раза;

• 2)    в основу определения кадастровой стоимости СПб ГУ «Кадастровая оценка» (далее – ГУ) положены следующие базовые принципы:

• •    кадастровая стоимость определялась как рыночная;

• •    применялся только сравнительный подход по рыночным данным;

• •    применялась мультипликативная модель (линейная регрессия для логарифмов рыночных цен) с учетом ряда ценообразующих факторов.

Подробно эти принципы изложены в отчете об оценке [2] (см. том 1 пункт 4.9.5, страницы 107, 111, 138). Как следует из комментариев, вынесенных в Приложение 9 к отчету, допускается логарифмическая нормальность распределения цен (с. 2 Приложения 9).

Осторожность, с которой в отчете говорится о возможности логарифмически нормального распределения, понятна, поскольку из этого следует необходимость проверки статистических гипотез, представляющих определенную трудность для больших выборок. В отчете [2] использован привычный и хорошо себя зарекомендовавший регрессионный анализ для линейной регрессии логарифмов рыночных цен (линейная регрессия помещена в показатель степени экспоненты, если иметь в виду натуральные значения цен). В этом случае необходимо проверять комплекс условий теоремы Гаусса-Маркова, так как регрессионный анализ разработан для случаев, когда о виде закона распределения ничего не известно. При выдвижении статистической гипотезы о совместной нормальности логарифмов аналогично необходимо проверить гипотезу о нормальности логарифмов (отличие заключается в ненулевом среднем, оно легко устраняется центрированием). В настоящей статье мы используем этот подход 2 для кластера, как представляется, адекватно отражающего рыночные изменения на рынке жилой недвижимости. Принятие гипотезы о совместной нормальности логарифмов означает, что линейной регрессией с наилучшими оценками параметров в смысле несмещенности, эффективности и состоятельности будет уравнение линии главной оси эллипсов рассеяния. Для остальных кластеров для построения линейных трендов будет применяться метод наименьших квадратов (далее – МНК).

Далее будет использоваться как термин «кадастровая стоимость» (КС), так и термин «рыночная стоимость» (РС), имея в виду, что это удельные стоимости одного квадратного метра площади жилой недвижимости. При проведении кадастровой оценки в 2015 году действовала редакция ФСО № 4 [6], где «под кадастровой стоимостью понимается установленная в процессе государственной кадастровой оценки рыночная стоимость объекта недвижимости». В Федеральном законе от 3 июля 2016 года № 237-ФЗ «О государственной кадастровой оценке» (далее – Закон № 237-ФЗ) кадастровая стоимость определена как «стоимость объекта недвижимости, определенная в порядке, предусмотренном Законом № 237-ФЗ, в результате проведения государственной кадастровой оценки в соответствии с методическими указаниями о государственной кадастровой оценке или в соответствии со статьей 16, 20, 21 или 22 указанного Федерального закона». Это обстоятельство стало причиной дискуссии в оценочном сообществе, так как определение кадастровой стоимости в Законе № 237-ФЗ утратило указание на содержательную часть кадастровой стоимости, а именно пропало указание на связь с рыночной стоимостью 3. Подробный анализ возникающих противоречий был представлен в статье [8].

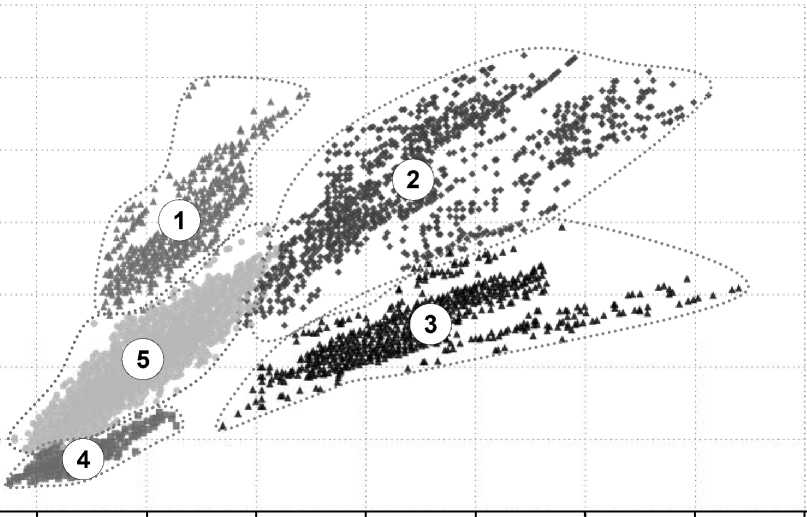
Рассмотрим двумерную случайную величину – кадастровая стоимость одного квадратного метра жилой недвижимости в 2015 и в 2018 годах – на конкретном примере – кадастровая стоимость отдельных квартир в городе Санкт-Петербурге. На рисунке 1 представлена соответствующая точечная диаграмма. Объем выборки – 2 025 757 объектов.

о л

50       100       150      200      250      300      350      400

V 2015 , ТЫС. р.

Рис. 1. Двумерное распределение кадастровых стоимостей одного квадратного метра квартир в городе Санкт-Петербурге в 2015 и 2018 годах

Даже визуально заметно, что весь рынок жилой недвижимости Санкт-Петербурга с точки зрения динамики изменений кадастровой стоимости распадается на ограниченное число кластеров (наличие второй координаты дает возможность разделить смесь распределений на компоненты, в одномерном случае сделать это намного сложнее). Более глубокое разбиение может привести к образованию большого числа компактных кластеров, которые могли бы быть интерпретированы как множества объектов сравнения. При этом в одном компактном кластере могут оказаться объекты не обязательно с одинаковыми значениями ценообразующих факторов.

Здесь проведено разбиение, показанного на рисунке 1 множества, на кластеры методами иерархического кластерного анализа с ограничением пять кластеров 4. Применение методов кластерного анализа представляется оправданным, так как возникает необходимость в «автоматическом» разделении сливающихся областей. Номера кластеров показаны на диаграмме (нумерация по часовой стрелке). Оказалось, что первые четыре кластера имеют характерные значения только одного ценообразующего фактора – тип дома.

Кластер 1 (5 042 объекта) – квартиры, отнесенные ГУ к типу дома «бизнес» и «элита» 5, кадастровая стоимость которых значительно повысилась.

Кластер 2 (8 351 объект) – квартиры, отнесенные ГУ к типу дома «бизнес» и «элита», кадастровая стоимость которых как повысилась (точки, лежащие выше биссектрисы первого квадранта), так и понизилась.

Кластер 3 (4 227 объектов) – в основном квартиры, отнесенные ГУ к типу дома «СФ» и «СФКР» 6, как правило, в зданиях старой постройки известных архитекторов, с хорошей локацией, часть зданий современной постройки, кадастровая стоимость которых снизилась.

Кластер 4 (2 801 объект) – квартиры, отнесенные ГУ к типу дома «дер» 7, кадастровая стоимость которых значительно снизилась.

Следует отметить, что первые четыре кластера в сумме составляют всего 1 процент от объема пятого кластера.

Кластер 5 (2 005 336 объектов) – все остальные квартиры Санкт-Петербурга. Этот кластер представляет собой смесь двумерных распределений кадастровой стоимости одного квадратного метра жилой недвижимости с разными значениями ценообразующих факторов. Он тоже может быть разделен на подмножества (кластеры) с использованием фиксированных значений ценообразующих факторов. Получаемые таким образом кластеры характеризуются относительно близкими средними значениями и, скорее всего, близкими тенденциями роста.

Таким образом, есть основания полагать, что пятый кластер в наибольшей степени соответствует состоянию рынка, а возможные ошибки расчетов КС не оказывают существенного влияния на эмпирическое распределение кадастровых стоимостей в этом кластере. Напротив, первые четыре кластера являются свидетельством того, что кадастровые стоимости входящих в них объектов претерпели значительные корректировки, отличающиеся от общей тенденции рынка и, возможно, иногда по причинам нерыночного характера.

Необходимо отметить, что в 2015 году ГУП ГУИОН определял кадастровую стоимость как рыночную (ФСО № 4). В условиях действующего Закона № 237-ФЗ ГУ, как следует из отчета, нашлись достаточно убедительные аргументы для определения КС2018 как рыночной стоимости. В связи с этим естественно предположить, что на рисунке 1, по сути, представлено эмпирическое двумерное распределение случайной величины РС2015, РС2018 в удельных единицах (за 1 кв. м), как их понимали ГУП ГУИОН в 2015 и ГУ в 2018 годах. Очевидно, что у этого распределения существует определенная структура, к ней могла бы быть подобрана модель, на основании которой могут быть сделаны расчеты, позволяющие решать широкий круг оценочных и аналитических задач. Выделим три:

• 1)    возможности оспаривания кадастровой стоимости;

• 2)    оценка темпов роста рынка;

• 3)    расчет корректировок для групп объектов сравнения.

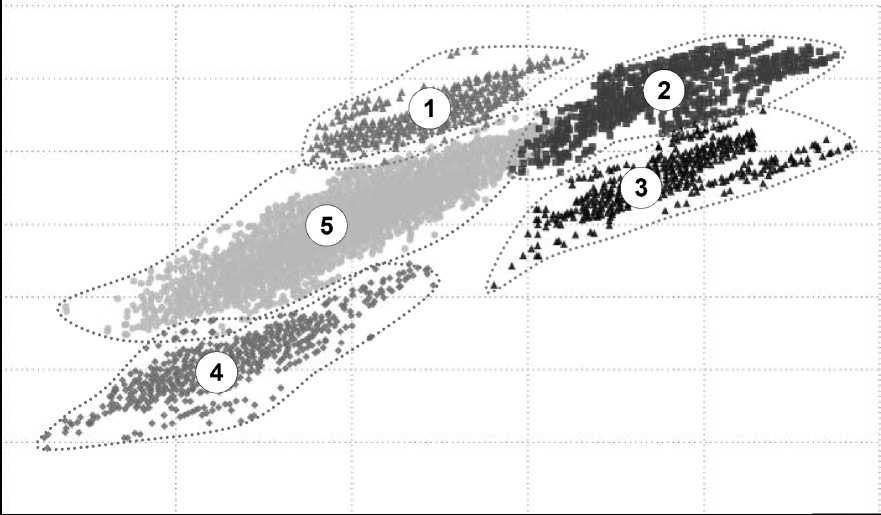
Преобразуем координатную плоскость первого рисунка, логарифмируя координаты V ₂₀₁₅ и V ₂₀₁₈. Результат показан на рисунке 2.

6,0

5,5

5,0

4,5

4,0

3,5

3,0

2,5

4,0

5,0

4,5

5,5

6,0

lⁿ V 2015

Рис. 2. Двумерное распределение натуральных логарифмов кадастровых стоимостей квартир в городе Санкт-Петербурге в 2015 и 2018 годах

В логарифмической плоскости сохранилось расположение кластеров относительно друг друга, но «облака» рассеяния приняли вид, похожий на эллиптический, указывающий на основания для выдвижения гипотезы о совместном нормальном распределении логарифмов кадастровых стоимостей одного квадратного метра квартир в 2015 и 2018 годах. Главные оси «эллипсов» рассеяния имеют близкие углы наклона.

Сравнивая рисунки 1 и 2, можно увидеть, что линейные тренды кластеров целесообразнее искать в логарифмической плоскости. Тогда уравнение линейного тренда вида In y = a x ln x + b при обратном переходе от логарифмов к «натуральным» значениям примет следующий вид:

• y = B x x^a , где B = e^b .

Применительно к рассматриваемой задаче для логарифмов будем искать линейный тренд:

ln V 2018 = a x ln V 2015 + b (для кластеров на рисунке 2).                                    (1)

А для натуральных значений КС будем искать тренд в виде степенной функции:

V ₂₀₁₈ = B ( V ₂₀₁₅ ) a (для кластеров на рисунке 1).                                           (2)

Предположение о совместном логарифмически нормальном распределении означает, что уравнение линии главной оси эллипсов рассеяния и есть линейная регрессия для логарифмов кадастровых стоимостей. Необходимые формулы легко получаются записыванием хорошо известных соотношений совместного нормального закона распределения для обозначений текущей задачи. Ранее они были показаны в работе [3].

Пусть V ₂₀₁₅ распределено логарифмически нормально с параметрами μ ₂₀₁₅, σ ₂₀₁₅, а V ₂₀₁₈

распределено логарифмически нормально с параметрами μ₂₀₁₈, σ ₂₀₁₈, коэффициент корреляции – ρ . Тогда уравнение главной оси эллипсов рассеяния принимает вид:

ln ^V 2018 ⁼ ρ ^{×      ×} ln ^V 2015 ⁺ μ 2018 ^- μ 2015 ^× ρ ^×       .

σ 2015                                 σ 2015

А уравнение степенного тренда в натуральных значениях (для кадастровых стоимостей) принимает вид:

ρ ^σ 2018 ^× ( ^V 2015 ) ^{σ 2015 .}

• ^V 2018 ⁼ exp ⎜ μ 2018 ^- μ 2015 ^× ρ ^×⎟

  ⎝                    σ 2015 ⎠

То есть в приведенных обозначениях получаем:

a = ρ ×

σ 2018 ;

σ 2015

b = μ ₂₀₁₈ - μ ₂₀₁₅ × ρ × .                                                                  (4)

σ 2015

В случае сохранения гипотезы о совместном логарифмически нормальном распределении формула (3) дает уравнение главной оси эллипсов рассеяния для логарифмов кадастровых стоимостей, которое автоматически является линией регрессии первого порядка, а параметры, определенные по формуле (4), совпадают с оценками, полученными по МНК, и являются наилучшими в смысле несмещенности, эффективности и состоятельности. Если о виде распределения ничего не известно (не удалось сохранить в качестве рабочей гипотезу о совместной нормальности логарифмов), то уравнение (3) является просто уравнением линейной регрессии 8.

Возможности оспаривания кадастровой стоимости

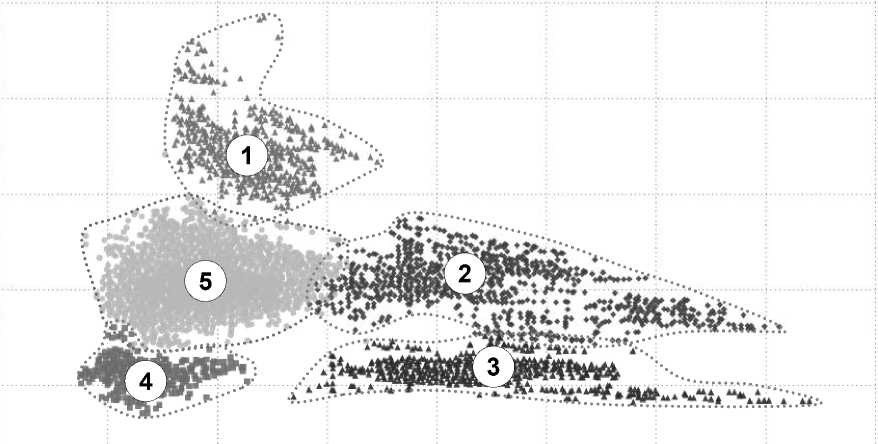
Предположим, что оценщику надо принять решение о заключении договора на оценку с целью замены кадастровой стоимости на рыночную. То есть ответить на вопросы, даст ли индивидуальная оценка заметную разницу между КС и РС, есть ли основания для отнесения объекта к иному кластеру, насколько сильно отклоняется точка с координатами V2015, V2018 для объекта оценки от основного тренда в кластере. Положение такой точки вблизи или ниже линии тренда свидетельствует о том, что пересмотр кадастровой стоимости либо не имеет перспективы, либо может привести к обратному результату. Поскольку с момента кадастровой оценки, проведенной в 2015 году, прошло уже 4 года и есть результаты кадастровой оценки 2018 года, скорее всего, собственники объектов, кадастровая стоимость которых не увеличилась, ничего оспаривать не будут. Иначе могут вести себя собственники объектов, кадастровая стоимость которых увеличилась (иногда значительно). На рисунке 1 такие объекты расположены выше биссектрисы первого квадранта. Более наглядным является рисунок 3, на котором показано удорожание кадастровой стоимости (отношение V2015 к V2018). Потенциально оспаривать кадастровую стоимость могут владельцы объектов, для которых вторая координата на рисунке 3 больше 1. Чем выше отклонение от единицы, тем больше у владельца оснований для оспаривания кадастровой стоимости.

2,5

2,0

1,5

1,0

0,5

150       200

250      300      350      400

V 2015 , ТЫС. р.

Рис. 3. Двумерное распределение кадастровой стоимости одного квадратного метра жилой недвижимости в городе Санкт-Петербурге в 2015 году и ее удорожания в 2018 году

Для каждого кластера можно построить соответствующий тренд и по близости координат объекта оценки к линии тренда судить о том, можно ли начинать процесс оспаривания кадастровой стоимости. В случае близости к линии тренда судебная перспектива не кажется обнадеживающей, так как кадастровая стоимость установлена «как у всех». В случае значительных отклонений потребуется углубленное исследование по определению рыночной стоимости. Кроме того, некоторые собственники могут рассматривать вопрос о «попадании не в тот кластер», например собственники объектов 1 кластера, который весь значительно подорожал (от ~ 40 до ~ 140 процентов).

Дополнением при определении вопроса, насколько возможно изменение кадастровой стоимости в результате индивидуальной оценки, может служить следующее: кадастровая стоимость определена по медианным значениям (это не противоречит Закону № 237-ФЗ [7]) и находится в русле привычного в сообществе понимания рыночной стоимости. Этому есть объяснение – использовался метод регрессионного анализа, то есть принята линейная модель для логарифмов рыночных цен. При потенцировании получена мультипликативная модель в виде экспоненты с линейной функцией в показателе степени ⁹. Поскольку гипотеза о виде распределения не выдвигалась, нет оснований корректировать данные мультипликативной модели. Но при логарифмически нормальном распределении цен потенцирование средних значений логарифмов дает всего лишь медиану закона рас пределения. Р ыночная стоимость ¹⁰ по определению находится не в медиане, а в моде.

Таким образом, чтобы получить РС надо КС умножить на мультипликатор e ^{- σ 2} (показано в статье [10]), где σ – стандартное отклонение стоимости одного квадратного метра по рыночным данным. В городе Санкт-Петербурге этот показатель с течением времени мало меняется и для различных секторов жилого рынка находится в пределах 0,15–0,25 (увеличиваясь вместе с ростом средних значений по секторам), для премиум-сегмента этот показатель может превышать 0,35. Корректировку можно оценить по приближенной формуле e ^{- σ 2} ≈ 1 - σ ² , то есть при σ = 0,15; 0,25; 0,35 КС выше РС (на 2,25; 6,25 и 12,25 процента соответственно). Для принятия решения об изготовлении отчета об оспаривании кадастровой стоимости это тоже следует учитывать, так как совокупность перечисленных обстоятельств позволит оценить возможное отличие рыночной стоимости от кадастровой при индивидуальной оценке ¹¹.

Оценка темпов роста рынка

Исходные допущения:

• •    темпы роста (изменения) рыночных цен в разных кластерах разные;

• •    в 2015 году кадастровая стоимость определена как рыночная, в 2018 году, несмотря на отсутствие в законодательстве указания на то, что кадастровая стоимость должна определяться как рыночная, расчеты кадастровой стоимости выполнены как рыночной стоимости. То, что кадастровая стоимость определена по медианным значениям не влияет на анализ динамики, так как поправочные коэффициенты все равно либо сократятся, либо, оказавшись близкими, при делении дадут значения, мало отличающееся от единицы.

  Поскольку, с одной стороны, V ₂₀₁₈ = exp _⎜ μ ₂₀₁₈ - μ ₂₀₁₅ × ρ ×

  
  

  σ 2018 ⎞

  σ 2015 ⎠

  
  

  ρ ^σ 2018

  × ( V ₂₀₁₅ ) ^{σ 2015}, а с другой –

  
  

  по формуле сложных процентов V ₂₀₁₈ = (1 + i )³ × V ₂₀₁₅, где i – темп роста рынка в год, получаем:

1 + i = exp

1 ⎛

3 ⎜_⎝ μ 2018 ^- μ 2015 ^× ρ ^×

σ 2018 ⎞

σ 2015 ⎠

1    ^σ 2018 _-1

3 ( ρ ^σ 2015 ) ( ^V 2015 )            .

Из приведенной формулы следует:

• •    кластеры (фактически секторы рынка) демонстрируют разную динамику;

• •    внутри кластера объекты с разной кадастровой стоимостью в 2015 году имеют разные темпы роста;

• •    при конструировании ставок дисконтирования и коэффициента прямой капитализации в рамках доходного подхода следует учитывать, как менялся рынок в предшествующем «кадастровом периоде». Для каждого объекта такой показатель i может

ночную стоимость: по средним арифметическим, по медианным или по модальным значениям. При нормальном распределении цен все три оценки одинаковы, но при несимметричных распределениях это не так.

быть определен по кадастровой стоимости прошлого периода (в данном случае – по 2015 году).

Для указанных кластеров полученные результаты сведены в таблице 1.

Таблица 1

Параметры распределений кадастровой цены 1 квадратного метра жилой недвижимости, коэффициенты линейной регрессии в логарифмах и коэффициенты расчета степенных функций для темпов роста

Кластер	μ 2015	μ 2018	σ 2015	σ 2018	ρ	а	в	B	Множитель	Показатель степени
1	4,754	5,282	0,148	0,144	0,880	0,856	1,211	3,356	1,497	-0,048
2	5,347	5,389	0,166	0,162	0,715	0,696	1,670	5,311	1,745	-0,101
3	5,354	4,810	0,136	0,156	0,825	0,946	-0,255	0,775	0,919	-0,018
4	4,099	3,529	0,166	0,172	0,886	0,918	-0,236	0,790	0,924	-0,027
5	4,511	4,513	0,134	0,154	0,941	1,088	-0,393	0,675	0,877	0,029

Примечание : в колонке «Множитель» указан коэффициент уравнения (5), в колонке «Показатель степени» – показатель степени в том же уравнении.

Параметры распределений, указанные в таблице 1 для кластеров 1–4, являются выборочными параметрами, с помощью которых рассчитываются коэффициенты формул (4) и (5). Для кластера 5 – это параметры совместного нормального закона распределения логарифмов.

Проверка гипотезы о совместной нормальности логарифмов для кластера 5

Нулевая гипотеза: логарифмы величин V ₂₀₁₅ , V ₂₀₁₈ распределены совместно нормально. В статье [5] представлен круговой тест, позволяющий проверять гипотезу о совместном нормальном распределении двумерного вектора. Он заключается в применении обычных одномерных тестов при любом угле поворота облака рассеяния. Поскольку объем кластера 5 превышает два миллиона объектов, применить обычные тесты невозможно (они существенно зависят от объема выборки), поэтому проверка гипотезы о совместной нормальности логарифмов будет проведена на малых подвыборках.

Последовательность действий:

• •    удаление крайних значений;

• •    бутстреп-анализ (извлечение с возвратом подвыборок меньшего размера из исходной выборки, проверка теста на совместную нормальность и многократное повторение этой процедуры);

• •    проверка распределения средних значений и стандартных отклонений полученных подвыборок, их соответствие среднему значению и стандартному отклонению исходной выборки.

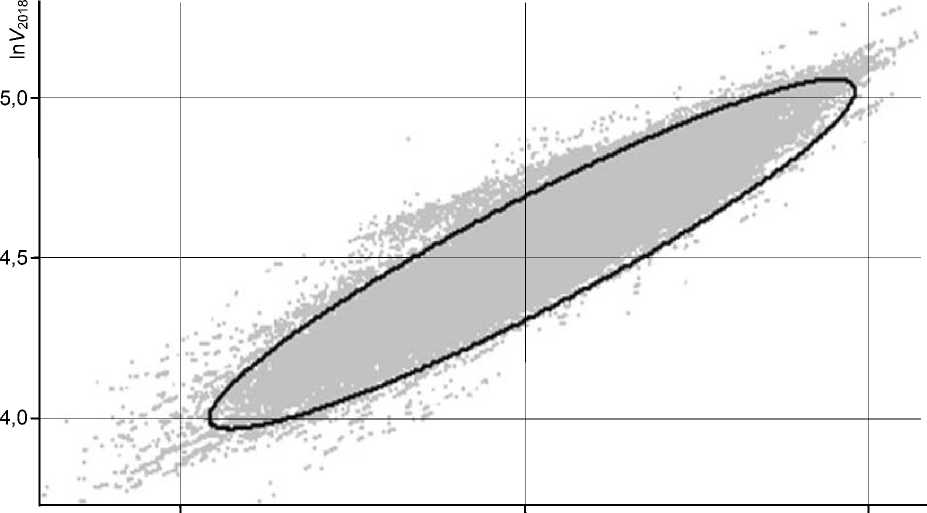
На рисунке 4 показано все множество точек кластера 5 (в логарифмах кадастровых стоимостей) и эллипс, содержащий 95 процентов от всех точек множества. Удаление крайних значений в двумерном случае означает удаление крайних значений по любой прямой, проходящей через точку с координатами, равными средним значениям компонент, то есть всех точек, оказавшихся вне эллипса.

4,0

4,5

5,0 ln V 2015

Рис. 4. Кластер 5 и эллипс, содержащий 95 процентов от всего множества экспериментальных точек

После удаления крайних значений образована новая выборка, для которой проводилось тестирование на соответствие совместному нормальному закону распределения. На рисунке 5 показаны результаты тестирования.

0,0

1,0

0,8

0,6

0,4

0,2

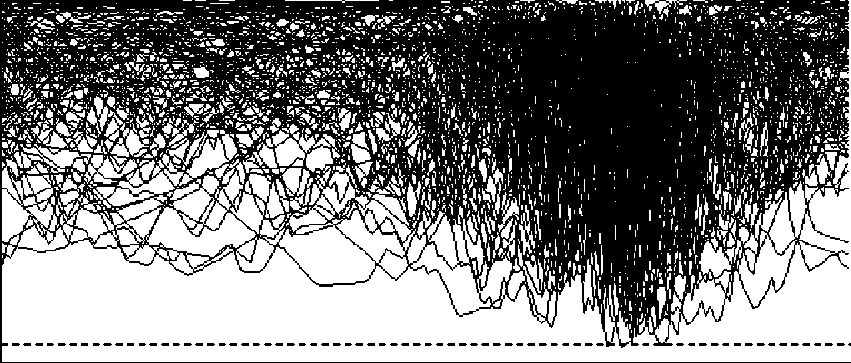
150 угол поворота^

Рис. 5. Значения p-value теста Колмогорова-Смирнова для кластера 5 (пунктиром отмечен критический уровень 5 процентов)

С помощью генератора случайных чисел выбиралось по 100 двумерных точек из исходной выборки и запускался круговой тест Колмогорова-Смирнова (см. [5]) для углов поворота от 0 до 180 º . Линия, показывающая соответствующее значение p-value , не должна опускаться ниже критического уровня 5 процентов. На рисунке 5 показано 100 повторений этой про цедуры ¹². Из 1 00 линий только 3 пересекли линию критического уровня 5 процентов.

Результаты теста позволяют сохранить гипотезу о совместном нормальном распределении логарифмов кадастровой стоимости в кластере 5 как рабочую. В таблице 2 приведены данные о средних, стандартных отклонениях: кластер 5, кластер 5 после удаления 5 процентов крайних значений по повторным выборкам.

Таблица 2

Средние и стандартные отклонения для кластера 5 после удаления

5 процентов крайних значений

Параметр	Значение
	исходное	после удаления 5 процентов крайних значений	среднее по повторным выборкам
μ 2015	4,511	4,511	4,509
μ 2018	4,514	4,513	4,510
σ 2015	0,136	0,134	0,133
σ 2018	0,157	0,154	0,152

Таким образом, уравнение линии главной оси эллипсов рассеяния (формула (3)) является линейным трендом с наилучшими оценками параметров a и b . Для остальных кластеров подобное тестирование не дало возможности опираться на гипотезу о совместной нормальности логарифмов. В связи с этим формула (3) дает только уравнение линейной регрессии для кластеров 1–4, определенной по МНК. В таблице 3 приведены значения коэффициентов a и b, полученные стандартной функцией «lm» статистического пакета R (они, естественно, совпадают со значениями, приведенными в таблице 1). В таблице 3 также показаны параметры, по которым обычно судят о качестве оценки параметров линейного тренда – коэффициент детерминации R ², медианные ( median ), максимальные ( max ) и минимальные ( min ) значения ошибок модели, стандартная ошибка остатков ( RSE ).

Таблица 3

Параметры линейных трендов, полученных по МНК

Кластер	а	в	R 2	min	median	max	RSE
1	0,856	1,211	0,744	-0,287	0,002	0,364	0,068
2	0,696	1,670	0,512	-0,354	-0,017	0,249	0,113
3	0,946	-0,255	0,681	-0,327	0,001	0,284	0,088
4	0,918	-0,236	0,785	-0,461	0,012	0,346	0,078
5	1,088	-0,393	0,886	-0,191	-0,005	0,194	0,052

Дополнительное исследование распределений остатков показало, что стандартная функция «fitdistr» пакета R, примененная к стьюдентизированным остаткам (стандартная функция «rstudent» пакета R) для всех пяти кластеров, предлагает как наилучшее приближение плотность стандартного нормального распределения N(0,1). Подставляя значения параметров из таблицы 3 в формулу (5), получаем темпы роста рынка в каждом кластере (в виде коэффициента мультипликатора 1 + i ). При этом кластер 5 (99 процентов от всей исходной выборки) будем считать подчиняющимся совместно нормальному закону распределения логарифмов кадастровых стоимостей. Для остальных кластеров закон распределения не определен. Вероятно, для объектов, оказавшихся в кластерах 1–4, корректировка кадастровой стоимости проводилась с исправлением неточностей, допущенных в 2015 году, и была обусловлена не только рыночными причинами.

V ₂₀₁₅, тыс. р./кв. м

—•-Кластер 1    • Кластер 2 —о—Кластер 3    * Кластер 4 —в—Кластер 5

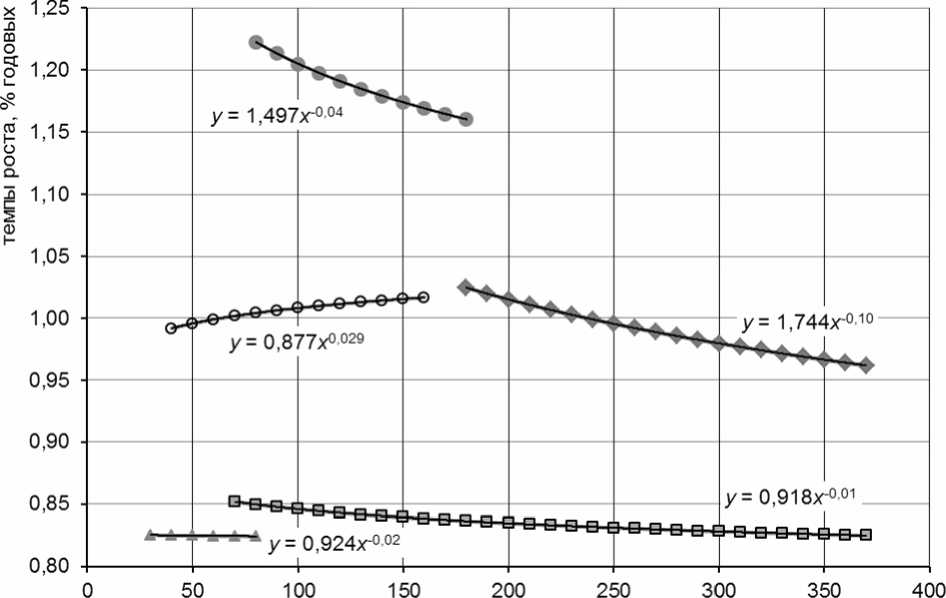
Рис. 6. Годовые темпы роста рынка жилой недвижимости по пяти кластерам (для всех кластеров для графиков трендов R ² = 1)

Из данных, представленных на рисунке 6, следует:

• •    диапазон темпов роста рынка в кластере 1 примерно от +22 до +17 процентов годовых, убывает по мере роста V ₂₀₁₅;

• •    диапазон темпов роста/падения рынка в кластере 2 приблизительно от +3 до -4 процентов годовых, убывает по мере роста V ₂₀₁₅;

• •    диапазон темпов падения рынка в кластере 3 приблизительно от -15 до -17,5 процента годовых, убывает по мере роста V ₂₀₁₅;

• •    диапазон темпов падения рынка в кластере 4 примерно от -16 до -19 процентов годовых;

• •    диапазон темпов роста/падения рынка в кластере 5 приблизительно от

  • - 2,5 до +1,7 процента годовых, возрастает по мере роста V ₂₀₁₅.

При оценке темпов роста рынка в кластерах использованы оценки параметров трендов, полученные исходя из гипотезы о совместном нормальном распределении логарифмов кадастровых стоимостей для кластера 5. Для кластеров 1–4 оценки параметров получены методом наименьших квадратов. Представляется, что темпы роста в кластере 5 (99 про центов от всей исследуемой совокупности) отражают динамику рынка масс-маркета, темпы роста в кластере 2 – динамику в секторе объектов классов «бизнес» и «элита». Темпы роста в кластере 1, по-видимому, обусловлены как изменениями городской среды (например ввод в эксплуатацию в 2016 году новой платной дороги «Западный Скоростной Диаметр», повлиявший на рыночную стоимость близлежащих объектов), так и иными причинами. Темпы изменений в кластере 3, по всей вероятности, не являются отражением рыночных изменений в секторе дорогой недвижимости, скорее всего, они отражают коррекцию кадастровой стоимости, обусловленную различными причинами нерыночного характера. Темпы изменений в кластере 4, по-видимому, отражают коррекцию стоимости объектов, расположенных в деревянных зданиях.

Расчет корректировок для групп объектов сравнения

Поскольку существуют традиционные замечания к методу парных сравнений и вытекающим из него корректировкам, полученным по малым выборкам, можно построить корректировки, основанные на сравнении больших объемов данных. Полагая, что результаты кадастровой оценки отражают текущее состояние рынка, можно продолжить разбиение множества всех точек кадастровых цен V ₂₀₁₅, V ₂₀₁₈ на более мелкие кластеры по ценообразующим факторам. Объектами сравнения являются все объекты, имевшие в 2015 году одинаковую кадастровую стоимость. Объекты из того же кластера, что и объект оценки, корректировки не требуют. Объекты из других кластеров могут быть откорректированы (все вместе) ¹³.

Пусть кластер, в который входит объект оценки, имеет тренд в виде степенной функции (верхние индексы означают: оо - объект оценки, ос - объект сравнения) V ₂ ^o ₀ ^o ₁₈ = B 1 ( V 2015 ) a ¹ (6), а кластер, в котором находится объект сравнения, имеет тренд V ₂ ^o ₀ ^c ₁₈ = B ₂ ( V ₂₀₁₅ ) ^{a 2} (7).

_B a 1

Тогда, подставляя V 2015 из (7) в (6), получаем V 20 ^o ₁₈ = 1-^ ( V ₂ ^o ₀ ^c ₁₈ ) a ² , и коэффициент корректировки будет: ( B 2 ) a ²

oo

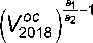
• ^V 2018 =   B L

\/oc       .    .O L

• ^V 2018     ( B 2 ) ^a 2

Для расчета корректировки нужна только кадастровая база. Такие корректировки могут быть основаны на обработке больших данных и положены в основу машинных расчетов и составления таблиц для широкого использования оценщиками. Для иллюстрации выбран простейший пример.

Пример корректировки на район

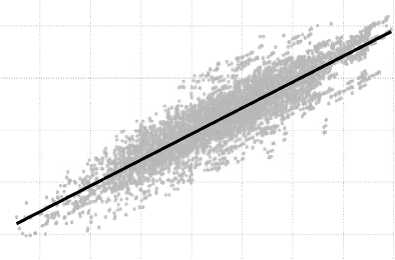
Пусть объект оценки находится во Фрунзенском районе, а объекты сравнения – в Невском районе (если объекты находятся в одном районе, то корректировка не требуется). На рисунке 7 показаны облака рассеяния логарифмированных кадастровых стоимостей, полученных в 2015 и 2018 годах, и соответствующие линейные тренды.

В таблице 4 представлены параметры распределений кадастровой стоимости одного квадратного метра жилой недвижимости в 2015 и 2018 годах для Невского района (в фор-

4,0

^4,6

4,4

4,0        4,2        4,4        4,6       4,8            4,2

lⁿ V 2015

g 4,8

4,6

4,4

4,0

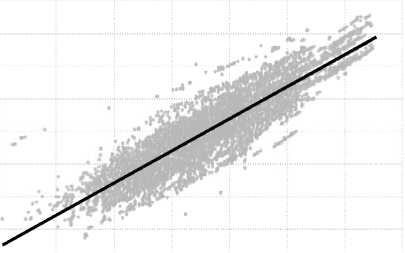
4,4         4,6         4,8

lⁿ V 2015

а)                                                     б)

Рис. 7. Облака рассеяния логарифмированных кадастровых стоимостей в 2015 и 2018 годах и линейные тренды для Невского района (а) и Фрунзенского района (б)

муле (8) индекс 2) и Фрунзенского района (в формуле (8) индекс 1), необходимые для подстановки в формулу (8).

Таблица 4

Параметры распределений кадастровой стоимости одного квадратного метра жилой недвижимости в 2015 и 2018 годах для Невского (индекс 2) и Фрунзенского (индекс 1) районов для подстановки в формулу (8)

Район     μ 2015 μ 2018 σ 2015 σ 2018   ρ    авB Множитель	Показатель степени
Невский      4,465 4,446 0,114 0,129 0,925 1,050 -0,240 0,786    1,107	-0,013

Фрунзенский 4,463 4,486 0,093 0,108 0,892 1,036 -0,138 0,871

Результаты расчетов показаны на рисунке 8.

Из полученных данных видно следующее:

• •    цена объекта-аналога в Невском районе для объекта оценки во Фрунзенском районе должна быть скорректирована в сторону увеличения;

• •    размер корректировки зависит от того, какая кадастровая стоимость была у объектов оценки, и сравнения (одинаковая!) в 2015 году, диапазон корректировки от 5,65 процента при V ₂₀₁₅ = 40 тысяч рублей за один квадратный метр до 3,8 процента при V ₂₀₁₅ = 160 тысяч рублей за один квадратный метр;

• •    с увеличением кадастровой стоимости одного квадратного метра площади размер корректировки уменьшается;

• •    экстраполяция за пределы указанного на рисунке 8 интервала не имеет смысла, в Невском и Фрунзенском районах в кластере 5 нет объектов с такой кадастровой стоимостью.

Выводы

• 1.    При принятии оценочными компаниями решений о подготовке отчета с целью пересмотра кадастровой стоимости как рыночной одной из возможных методик может быть следующая процедура:

• •    проведение глубокого кластерного анализа двумерных множеств точек кадастровых стоимостей за последние два кадастровых периода;

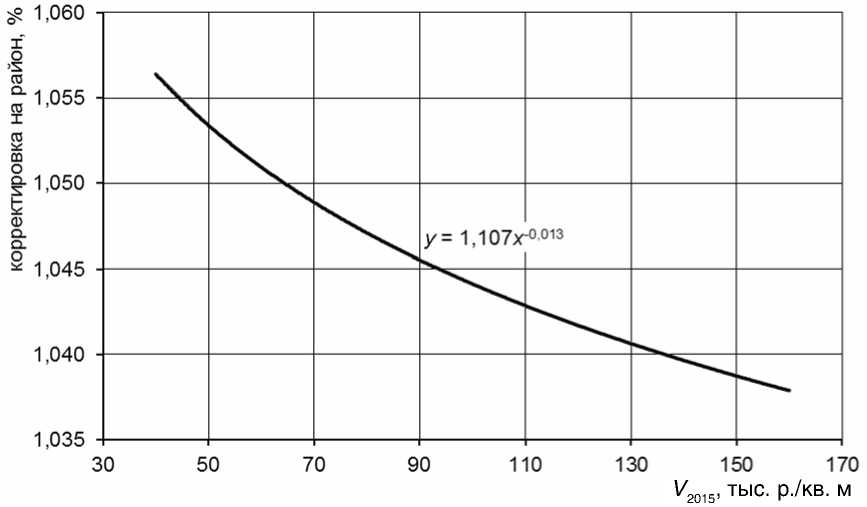
Рис. 8. Значения корректировок на район для случая, когда объект оценки расположен во Фрунзенском районе, а объекты сравнения – в Невском

• •    выявление тренда и определение геометрического места объекта оценки по отношению к общему тренду.

• 2.    Кадастровые базы могут быть данными для расчета рыночных показателей, указывающих на темпы роста секторов рынка. Они должны учитываться при конструировании коэффициентов дисконтирования и коэффициента прямой капитализации в рамках доходного подхода, так как часто просуммированные в расчетах премии за риски, требуемая доходность и т. д. не соответствуют текущему состоянию рынка.

• 3.    Кадастровые базы могут быть данными, на основании которых в рамках сравнительного подхода могут рассчитываться корректировки по различным ценовым факторам, основанные на обработке больших данных.

• 4.    Рынок оценочных услуг нуждается в создании обширных рыночных баз данных. Невозможно требовать от различных участников рынка, имеющих собственные интересы, издания баз в одном формате. Но включение в рыночные базы кадастрового номера становится важнейшей задачей, так как он является уникальным идентификатором, позволяющим объединить разные базы.

P. 17–21.

***

инк®м

НЕДВИЖИМОСТЬ

РЕФОРМА ДОЛЕВОГО СТРОИТЕЛЬСТВА ВЫЗВАЛА ВСПЛЕСК СПРОСА НА МОСКОВСКИЕ СТУДИИ

Специалисты Департамента новостроек ИНКОМ-Недвижимость исследовали предложение и спрос на квартиры-студии в столице. Так, хотя студиями представлены всего 4% экспозиции первичного жилья в Москве, их популярность за год возросла на 3 п.п., до 7% от общего числа сделок, а скорость реализации повысилась на 8%. Во многом причиной этого стал покупательский бум в преддверии реформы долевого строительства. При этом каждый третий клиент приобрел студию с целью сдачи в аренду или перепродажи, в то время как год назад покупателей-инвесторов в рамках этого формата насчитывалось не более 19%. Несмотря на его специфику, 70% представленных в ЖК студий сегодня продаются в первый же квартал реализации проекта. Даже при неудачной планировке такие квартиры находят своего владельца в течение 3-4 кварталов. За год средняя стоимость 1 кв. м в студии выросла на 9%, до 212 тыс. р., и дальнейшее повышение цен из-за увеличения себестоимости строительства тоже весьма вероятно. Впрочем, в условиях снижения реальных доходов граждан девелоперы могут найти выход из положения, предложив покупателю квартиры под ключ: сейчас объем таких лотов среди студий не превышает 5%.

В Америке и Европе формат квартир-студий популярен уже на протяжении более полувека, однако в России такое жилье массово стали строить только десять лет назад. Сегодня на первичном рынке Москвы студии занимают всего 4% предложения, за последние годы эта цифра серьезно не менялась.

Главной характеристикой студийной планировки в России является единое пространство, где нет разделения на жилую часть и кухню. 60% таких квартир имеют площадь 2025 кв. м, в 35% случаев метраж студии составляет 30-35 «квадратов», в 5% – лишь 15-18 кв. м. Чаще всего студия имеет форму узкого прямоугольника и одно окно, реже – квадратную форму и два окна. Также у нее может быть балкон, который владельцы нередко обустраивают как дополнительную жилплощадь.

• «В    бизнес- и премиум-классах квартиры-студии имеют площадь 100 кв. м и более, – рассказывает заместитель директора Департамента новостроек ИНКОМ-Недвижимость

Продолжение на с. 58