Калибровка скоринговой модели с учетом цензурированных данных
Автор: Широбокова Маргарита Александровна
Журнал: Вестник Пермского университета. Серия: Экономика @economics-psu
Рубрика: Экономико-математическое моделирование
Статья в выпуске: 3 т.14, 2019 года.
Бесплатный доступ
В связи с введением соглашения Базель II и МСФО (IFRS) 9 вопрос более точной оценки кредитного риска банка становится все более актуальным. В соответствии с указанным положением банки самостоятельно рассчитывают оценку кредитного риска, которая чаще всего строится на основе исторической выборки в виде скоринговой модели. Однако при построении скоринговой модели возникает проблема оценки кредитных договоров: они не доживают до срока, на который строился модельный прогноз, т. е. данные кредиты выбывают из наблюдения ранее даты окончания исследования. Такие кредиты принято называть цензурированными, и в разрезе проведенного нами исследования имеет место цензурирование справа. При этом влияние таких кредитных договоров на уровень банковской дефолтности значительно, а, следовательно, значение, которое выступает базой для калибрования скоринговой модели, также оказывает существенное влияние на оценку калибровочного коэффициента. Целью данного исследования является разработка инструментария решения проблемы учета цензурированных данных при калибровке скоринговой модели на этапе валидации. Рассмотрены разные способы учета цензурированных данных: 1) учет цензурированных кредитов как «хороших», 2) исключение цензурированных кредитов из выборки, 3) метод Каплана - Мейера, 4) метод взвешивания. При этом уделяется внимание актуальным вопросам не только оценки самой доли дефолтов с учетом цензурированных договоров, но и в первую очередь применения цензурированных данных при корректировке модельной оценки риска для валидации скоринговой модели. Для каждого метода учета цензурированных данных проанализировано влияние калибровочного коэффициента на соотношение модельного числа дефолтов к фактическому на основе использования трех методов калибровки модели - линейной калибровки от значений вероятностей, линейной калибровки от значений шансов, логарифмической калибровки от значений шансов. Построение расчетов производится на основе имеющихся данных по договорам и дефолтам регионального розничного банка. Сделан вывод о зависимости метода учета цензурированных данных от политики кредитной организации. В частности, установлено, что для организаций с низким уровнем риск-аппетита необходимо использовать метод исключения цензурированных кредитов, для организаций с высоким уровнем риск-аппетита целесообразнее учитывать цензурированные кредиты как «хорошие». В свою очередь, для получения более точного прогноза при адекватном уровне риск-аппетита рекомендуется использовать методы взвешивания цензурированных данных и Каплана - Мейера. Перспективы исследования составляет учет цензурированных данных не только на этапе валидации скоринговой модели, но и на первоначальном этапе ее построения.
Кредитный риск, коммерческий банк, вероятность дефолта, скоринговая модель, валидация скоринговой модели, цензурированные данные, методы учета цензурированных данных, калибровочный коэффициент, методы калибровки, риск-аппетит
Короткий адрес: https://sciup.org/147245735
IDR: 147245735 | УДК: 336.717.061, | DOI: 10.17072/1994-9960-2019-3-406-420
Текст научной статьи Калибровка скоринговой модели с учетом цензурированных данных
На сегодняшний день в условиях повышенной неопределенности развития финансо- вых отношений на мировом уровне усложняются системы управления рисками в банковской сфере [1; 2]. Одним из наиболее приоритетных направлений является управление кредитным риском, который зачастую оценивается на основе скоринговой модели1. Данный метод позволяет рассчитать вероят- ность наступления дефолта для конкретного заемщика в течение определенного периода времени. При этом дефолтом принято называть просрочку по основному долгу или процентам в течение 90 дней и более в течение первого года жизни кредита [3] (здесь и далее – год равен 365 дням). Тогда в качестве вероятности наступления дефолта PD (Probability of Default) принимается вероятность возникновения просрочки по основному долгу или процентам более 90 дней в течение первого года жизни кредита2. Однако наряду с задачей построения скоринговой модели актуальной является задача ди- намического контроля качества модели, что подразумевает постоянный контроль соответствия модельных оценок числа дефолтов их фактическому значению [4]. Проблемой выступает ситуация, в которой прогнозное число дефолтов может быть как завышен- ным, так и заниженным, по сравнению с фактическими данными. Построение новой скоринговой модели для устранения указанной проблемы является достаточно трудо- емким процессом, поэтому при управлении кредитным риском используется специальная процедура, называемая калибровкой модели, которая позволяет получить наиболее точную оценку вероятности дефолта, согласующуюся с фактическими значениями.
При проведении калибровки суще- ствует ряд вопросов, от которых зависит конечный результат модельной оценки уровня дефолта. Исследование методов калибровки модели произведено ранее в [5]. Дополнительной проблемой при калибровании моде- ли выступают кредитные договоры, которые не дожили до срока, на который строился модельный прогноз, т. е. данные кредиты выбывают из наблюдения ранее даты окончания исследования. Определение влияния таких кредитных договоров на уровень банковской дефолтности и его калибровку явля- ется основным направлением исследования.
Формулировка проблемы
Согласно классическому определению дефолта оценка уровня дефолтности кредитного портфеля производится в течение его первого года жизни1. Однако возникает вопрос учета кредитов, которые были закрыты в течение первого года жизни. Причиной закрытия кредита в данном случае могут выступать следующие ситуации: наступление срока погашения по договору, досрочное погашение, реструктуризация при одновременной выдаче нового кредита и др. Подобное отсутствие в данных части информации о наблюдениях за определенный промежуток времени или наличие неопределенности относительно возникновения интересующего события называется цензурированием, а сами данные – цензурированными [6]. Когда на конец исследования неизвестна информация о наблюдениях, то данные цензурированы справа. В противоположном случае, когда на момент начала исследования нет информации о наблюдениях, имеет место цензурирование слева. Ситуация, в которой по части данных неизвестна информация о наблюдениях на начало исследования, а по части – на конец исследования, называется двусторонним цензурированием [6]. В случае описанной ситуации оценки кредитного риска имеет место цензурирование справа: на конец периода наблюдения известен факт возникновения дефолта каждого клиента, однако произойдет ли дефолт за пределами исследования, неизвестно [7; 8].
Рассмотрим проблему влияния цензурированных данных на примере кредитования физических лиц регионального коммерческого банка. В качестве исследуемого периода выдачи кредитов возьмем 2016 г. Пусть в данный период действовала некоторая скоринговая модель (а именно application scoring ), по которой оценивались все заявки на кредит. При этом учтем, что построение скоринговой модели было стандартным, т. е. кредиты, не прожившие первый год, включались в обучающую выборку как положительные наблюдения [9–11].
В течение указанного периода был выдан 29 141 кредит, из которых 2 747 вышли в дефолт и 11 618 кредитов было закрыто в течение первого года жизни. Получаем, что в исследуемом портфеле 14 365 цензурированных договоров. Распределение фактического количества выходов в дефолт в каждый месяц жизни кредита в абсолютной величине выглядит следующим образом (рис. 1).
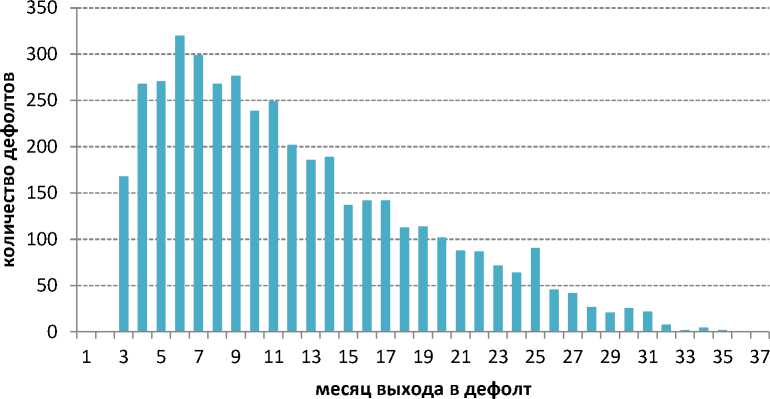
Рис. 1. Распределение фактического числа выходов в дефолт, абсолютная величина
Вопрос адекватности оценки возникает при построении распределения количества выходов в дефолт в относительных величинах. Основной проблемой выступает база оценки, для которой существует два подхода к учету цензурированных договоров: цензурированные кредиты по умолчанию принимаются как «хорошие» или же они полностью исключаются из анализа, и используются только кредиты, прожившие 12 месяцев жизни [7]. Получаем, что фактическая величина доли дефолтов на 12-м месяце жизни, которую необходимо оценить с помощью скоринговой модели, со- ставляет
2,00%
1,80%
1,60%
0,00%
0,60%
0,40%
0,20%
1,40%
1,20%
1,00%
0,80%
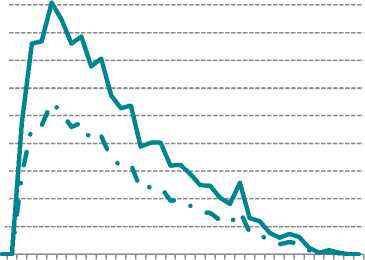
0 2 4 6 8 1012141618202224262830323436
Доля дефолтов с учетом цензурированных кредитов в качестве «хороших»
Доля дефолтов без учета цензурированных кредитов
PD 0 =
14873 + 11618 + 2747
= 0,0943
(9,43%)
или PDc=----2747----= 0,15 68 (15,68%), f 14873+2747 ’
где PD 0 - фактическая величина доли дефолтов на 12-м месяце жизни, а цензуриро-
ванные кредиты принимаются как «хорошие»; PD c - фактическая величина доли дефолтов на 12-м месяце жизни, а цензурированные кредиты исключаются из анализа.
Тогда доля дефолтов в зависимости от месяца выхода в дефолт будет выглядеть следующим образом (рис. 2), а кумулятивная доля соответственно (рис. 3).
Рис. 2. Распределение доли дефолтов
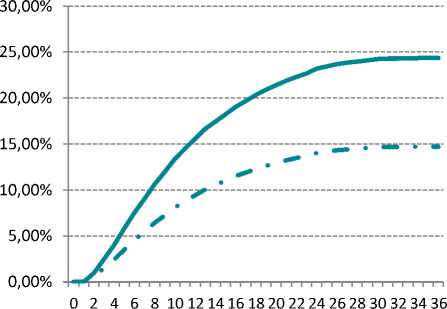
Кум. доля дефолтов с учетом цензурированных кредитов в качестве «хороших»
Кум. доля дефолтов без учета цензурированных кредитов
Полученная ситуация показывает, что различия в значениях доли дефолтов существенны (рис. 4). Сравним полученные фактические доли дефолтов с прогнозным моделируемым значением: текущая модельная оценка равна 24.18%, что значительно завышает фактическое значение риска, вне зависимости от способа учета цензурированных данных, и требуется калибровка модели. Тогда значение, которое будет выступать базой для калибрования модели, а также метод, который будет использоваться при калибровке, будет влиять на значение калибровочного коэффициента.
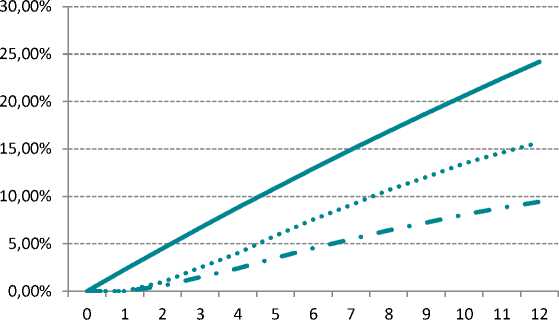
Кум. доля дефолтов с учетом цензурированных кредитов как «хороших»
Кум. доля дефолтов без учета цензурированных кредитов
Кум. доля дефолтов согласно модельной оценке
Рис. 4. Кумулятивное распределение фактической и модельной доли дефолтов за первые
12 месяцев
Всего существует три способа калибровки скоринговой модели - линейная калибровка от значений вероятностей, линейная калибровка от значений шансов, логарифмическая калибровка от значений шансов [5]. Применив все три способа к различным оценкам уровня дефолтности (рис. 5), видим, что значения коэффициента также существенно отличаются друг от друга.
0,90
0,80
0,70
0,60
0,50
0,40
0,30
0,20
0,10

Линейная Шансы Логарифм шансов
Рис. 5. Значения коэффициентов калибровки
Примечание: 1 - Доля дефолтов с учетом цензурированных кредитов в качестве «хороших»; 2 -Доля дефолтов без учета цензурированных кредитов.
Для получения более адекватной оценки доли дефолтов рассмотрим методы, позволяющие учитывать цензурированные договоры.
Методы исследования
Рассмотрим методы учета цензурированных данных: метод взвешивания цензурирован- ных данных и метод Каплана - Мейера. Введем следующие обозначения. Пусть всего в исследуемом портфеле N договоров, из которых D - количество договоров, по которым произошло событие де- фолта, а N - количество нецензуриро- ванных договоров, т. е. договоров, которые прожили более 365 дней со дня выдачи кредита и по которым не было выхода в дефолт согласно введенному ранее определению. Тогда количество цензурированных договоров, т. е. договоров, которые прожили более 365 дней со дня выдачи кредита вне зависимости от события дефолта, равно Ncens = N - N0 > D и включает в себя дефолтные договоры.
Метод взвешивания цензурированных данных
Метод взвешивания цензурированных данных предполагает, что кредиты, не прожившие оцениваемый первый год жизни, не исключаются из оценки, а входят в нее с индивидуальным весом w (w < 1), который зависит от числа прожитых дней кредитным договором [7]. Если кредитный договор нецензурированный, то вес равен w = 1. Если цензурированный кредитный договор прожил m дней (m < 365), то его доля составит w = m—. Если по кредиту 365
наступило событие дефолта, то его вес также равен w = 1 . Тогда общая доля дефолтов будет равна суммарному весу всех дефолтных кредитов (что равняется количеству дефолтов) по отношению к сумме весов по всему исследуемому портфелю:
w i^__D
PDw
= Z w = N 0 + z w ■ N N cens
Метод Каплана – Мейера
Метод Каплана - Мейера для оценки дефолтности учитывает только кредиты, которые прожили соответствующий срок. Пусть моменты наступления события дефолта по D объектам последовательно распределены на промежутке [0;те). Тогда для каждого момента времени t., i е[0; ю), п. - количество договоров, подверженных риску до момента времени t (договоры, не цензурированные до момента времени t и не подверженные событию дефолта), d. -количество дефолтов, произошедших к моменту t , а вероятность выживания рассчитывается как отношение выживших объектов к общему количеству наблюдений на момент начала наблюдения [12; 13]. Общая вероятность дожития до определенного момента времени рассчитывается как произведение всех вероятностей дожития до этого момента времени, что носит название функции Каплана - Мейера для функции выживания S (t):
PD km = s ( t ) =nf i - —1 (2) f 1| ^ n ( x ) )
Если договор покидает портфель ввиду цензурирования, то данное событие повлияет на количество объектов под риском n , но не на количество дефолтов d. Аналогично выданные новые договоры, попадающие в портфель в момент t , на момент времени t попадут в группу объектов, подверженных риску наступления дефолта. При этом функция Каплана -Мейера ‒ ступенчатая функция (рис. 6): функция не изменяется ни между событиями, ни в момент цензурирования, изменения происходят только в момент возникновения самого события [13; 14].
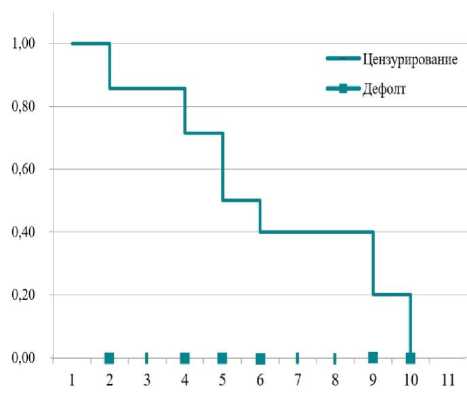
Рис. 6. Функция Каплана - Мейера
Сравнение методов учета цензурированных данных
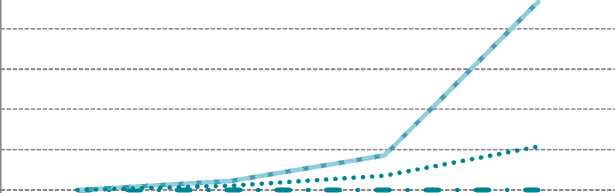
Различие оценки доли дефолтов в разрезе разных методов будет зависеть от портфельных данных. На примере искусственно созданного портфеля рассмотрим крайние случаи оценки. Пусть портфель состоит из N = 100 договоров, из которых D = 20 вышло в дефолт. Первая ситуация: по всем дефолтным договорам событие дефолта наступило в последний месяц жизни, а число нецензурированных договоров составляло N o = 100, 90, 70, 30 договоров соответственно. Кумулятивная доля дефолтов в зависимости от ситуации приведена на рис. 7.
70,00%
20,00%
о 60,00% н i 50,00% ф к 40,00%
30,00%
10,00%
0,00%
Рис. 7. Доля дефолтов для имитации первой ситуации
Наблюдаем, что при отсутствии цензурированных договоров при расчете каждым из приведенных методов значение доли дефолтов составляет 20%. При увеличении числа цензурированных договоров в портфеле доля дефолтов, когда цензурированные кредиты учитываются как «хорошие», не изменяется, при использовании других методов исследования доля дефолтов повышается, при этом в случае исключения цензурированных кредитов и применения метода Каплана – Мейера повышается значительно. Значения доли дефолтов в этом случае полностью совпадают ввиду отсутствия выходов в дефолт не в последний месяц жизни.
Рассмотрим вторую ситуацию: портфель также состоит из N = 100 договоров, из которых D = 20 вышло в дефолт, однако событие дефолта наступает в середине срока жизни кредита для N cens = 0, 5, 10, 15, 20 дефолтов соответственно, а число нецензурированных договоров для всех случаев составляло N = 90.
В данном случае наблюдается, что доля дефолтов, рассчитанная методом, когда исключаются цензурированные кредиты, и доля дефолтов, рассчитанная методом, когда цензурированные кредиты учитываются как «хорошие», принимают также максимальное и минимальное значения 22,22% и 20% соответственно (рис. 8). При этом наблюдается, что доля дефолтов изменяется только для метода Каплана – Мейера: при увеличении числа кредитов, вышедших в дефолт в середине срока жизни, доля дефолтов снижается с 22,22% до 20%.
Таким образом, получаем, что различие оценки доли дефолтов при расчете каждым из приведенных методов будет зависеть от кредитного портфеля, а именно от того, какие доли от общего размера кредитного портфеля занимают дефолтные и цензурированные кредитные договоры. В соответствии с этим интерес представляет исследование применения различных методик к реальному кредитному портфелю. Дальнейшее построение расчетов производится на примере регионального розничного банка.
24,00%
22,00%
20,00%
Рис. 8. Доля дефолтов для имитации второй ситуации
Результаты исследования
На основе имеющихся данных по договорам и дефолтам исследуем влияние указан- ных методов на расчет доли дефолтов по реальному портфелю. Согласно введенным величинам в портфеле N = 29141,
N o = 14873 , Ncens= 11618 + 2747 = 14365 ,
D = 2747. Для рассматриваемого кредитного портфеля сумма весов по всему портфелю оказалась
равной ^ w = 24422,3 3.
N
Тогда рассчитанная величина доли дефолтов для методов взвешивания цензурированных данных и Каплана – Мейера за первые 12 месяцев в сравнении со стандартными подходами оценки цензурированных данных будет выглядеть следующим образом (рис. 9).
Наблюдаем, что метод взвешивания и метод Каплана – Мейера принимают достаточно близкую оценку доли дефолта за первые 12 месяцев, при этом данная оценка выступает как нечто среднее между максимальным и минимальным значениями доли дефолтов, рассчитанных методом, когда исключаются цензурированные кредиты и когда цензурированные кредиты учитываются как «хорошие» соответственно. Сопоставим графики кумулятивного рас- пределения доли дефолтов за весь срок жизни кредитов (рис. 10) и в зависимости от месяца выхода в дефолт (рис. 3). Наблюдается изменение формы кривой по методу Каплана – Мейера, что напрямую связано с меньшим количеством договоров, вышедших в дефолт на более поздних сроках кредитования. Метод взвешенных долей, в свою очередь, форму кривой не меняет. Фактическая величина доли дефолтов на 12-м месяце жизни приведена в табл. 1.
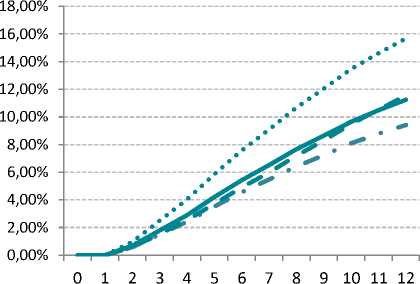
Кум. доля дефолтов с учетом цензурированных кредитов в качестве «хороших»
Кум. доля дефолтов без учета цензурированных кредитов
Кум. доля дефолтов в соответствии с методом Каплан-Мейера
Кум. доля дефолтов в соответствии с методом взвешивания
Рис. 9. Кумулятивное распределение доли дефолтов за первые 12 месяцев
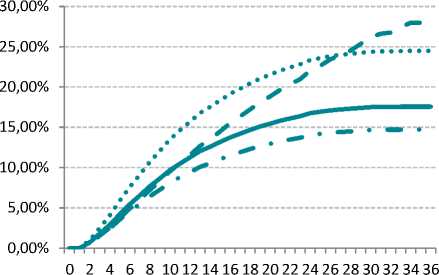
Кум. доля дефолтов с учетом цензурированных кредитов в качестве «хороших»
Кум. доля дефолтов без учета цензурированных кредитов
Таблица 1
Фактическая величина доли дефолтов на 12-м месяце жизни
|
Метод расчета |
Обозначе ние |
Доля дефолтов |
|
Доля дефолтов с учетом цензурированных кредитов в качестве «хороших» |
PD 0 |
9,43% |
|
Доля дефолтов без учета цензурированных кредитов |
PDc |
15,68% |
|
Доля дефолтов в соответствии с методом Каплана – Мейера |
PDkm |
11,54% |
|
Доля дефолтов в соответствии с методом взвешивания |
PDw |
11,25% |
Кум. доля дефолтов в соответствии с методом Каплан-Мейера
Кум. доля дефолтов в соответствии с методом взвешивания
Рис. 10. Кумулятивное распределение доли дефолтов за весь срок жизни кредитов
Таким образом, значение фактической величины доли дефолтов на 12-м месяце жизни может быть различным в зависимости от используемой методики, при этом введенные методы учета цензурированных данных имеют достаточно близкую оценку по исследуемому портфелю. Также сравним полученные фактические доли дефолтов с прогнозным моделируемым значением (рис. 11).
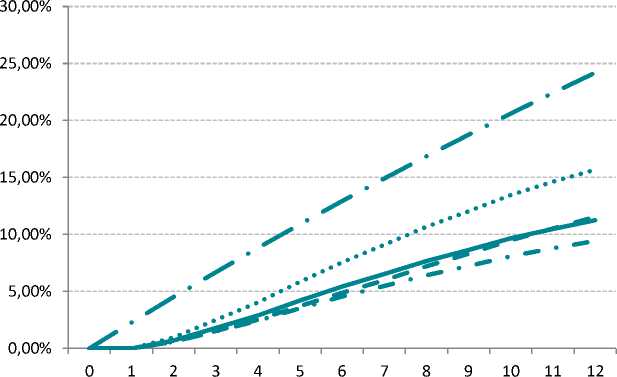
Кум. доля дефолтов с учетом цензурированных кредитов в качестве «хороших»
Кум. доля дефолтов без учета цензурированных кредитов
Кум. доля дефолтов в соответствии с методом Каплан-Мейера
Кум. доля дефолтов в соответствии с методом взвешивания
Кум. доля дефолтов согласно модельной оценке
Рис. 11. Кумулятивное распределение фактической и модельной доли дефолтов за первые
12 месяцев
Согласно рис. 12, применив все три способа к различным оценкам уровня де-фолтности, видим, что значения коэффициента калибровки, полученные без учета цензурированных данных, отражают крайние ситуации занижения фактического зна- чения кредитного риска и его завышения. При этом методы учета цензурированных данных, а именно метод взвешивания цензурированных данных и метод Каплана – Мейера, дают более корректную оценку значения коэффициента калибровки.
0,90
0,80
0,70
0,60
0,50
0,40
0,30
0,20
0,10
0,44 ♦ 0,39
______________ ■ 0,23
"4 0,79
0,65
■ 0,42
▲ 0,55
+ 0,48
■ 0,29
-4..........
0,54
0,47
♦ Линейная ■ Шансы ▲ Логарифм шансов
Рис. 12. Значения коэффициентов калибровки
Примечание: 1 – Доля дефолтов с учетом цензурированных кредитов в качестве «хороших»; 2 – Доля дефолтов без учета цензурированных кредитов; 3 – Доля дефолтов в соответствии с методом Каплан – Мейера; 4 – Доля дефолтов в соответствии с методом взвешивания.
Покажем влияние калибровки на модельные значения доли дефолтов в сравнении с фактическими значениями, рассчитанными разными методами, при помощи графиков соотношения PDf для PD m каждого метода калибровки [5]. Для этого будем использовать отсортированные значения расчетных вероятностей с учетом калибровочного коэффициента по заемщикам. Для каждой калибровки производится разбиение на интервалы так, чтобы в каждом интервале присутствовало равное количество договоров (в данном случае произведено разбиение по 1000 кредитов).
Сравнение указанных калибровок с
PD помощью расчета соотношения f и по-PD m строения соответствующих графиков по общему периоду показывает, что при логарифмической калибровке от значений шансов рассчитанные вероятности завышаются, для линейной калибровки от значений вероятностей и линейной калибровки от значений шансов показатели приблизительно одинаковы. В силу того что для рассмотренных данных мы получили, что линейная калибровка от значений вероятности несколько лучше отражает как текущий, так и последующие периоды, приведем графики только для этого способа калибровки (рис. 13).
При этом для всех способов калибровки наблюдается следующее. При калибровании с учетом цензурированных кредитов как «хороших» получаем крайнюю ситуацию завышения фактического значения кредитного риска, при исключении цензурированных кредитов ‒ занижения фактического значения. При этом методы, учитывающие недожившие кредиты (метод взвешивания цензурированных данных и метод Каплана – Мейера), позволяют получить более точную оценку кредитного риска в сравнении с фактическими значениями. Также отметим, что при использовании указанных методов калибровки графики ROC-кривых для модели до калибровки и моделей после калибровки совпадают, соответственно площадь под ROC-кривой и коэффициент Джини остаются неизменными [5].
1. Линейная калибровка, учет цензурированных кредитов в качестве «хороших»
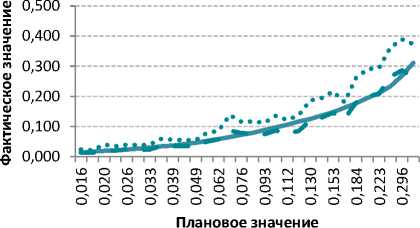
2. Линейная калибровка, без учета цензурированных кредитов
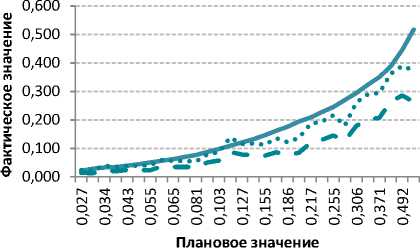
3. Линейная калибровка, метод Каплан-Мейера
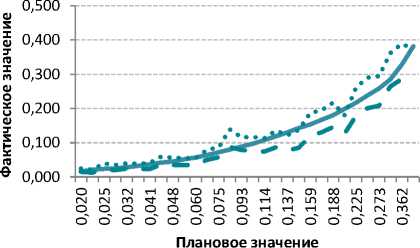
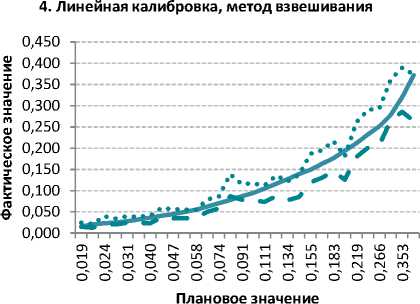
^"Прогнозный балл после проведения калибровки
-
— Фактические значения, учет цензурированных кредитов в качестве «хороших»
-
• • • Фактические значения, без учета цензурированных кредитов
Рис. 13. Отношение прогнозируемого числа дефолтов к фактическому
Несмотря на то что расчет балла заемщика, скорректированного с учетом линейной калибровки, проще в обслуживании, необходимо иметь в виду, что выбор
Таблица 2
Зависимость метода калибровки и учета цензурированных данных от политики кредитной организации
|
Политика кредитной организации |
Метод учета цензурированных данных |
Метод расчета калибровочного коэффициента |
|
Низкий риск-аппетит |
Исключение цензурированных кредитов |
Логарифмическая калибровка от значений шансов |
|
Адекватный риск-аппетит |
Метод Каплана – Мейера, метод взвешивания |
Линейная калибровка от значений вероятностей |
|
Высокий риск-аппетит |
Учет цензурированных кредитов как «хороших» |
Линейная калибровка от значений шансов |
Метод учета цензурированных данных будет зависеть от политики кредитной организации: для отображения наихудшей ситуации необходимо использовать метод исключения цензурированных кредитов, для наилучшей ‒ производить учет цензу- метода калибровки и калибровочного периода всегда зависит от имеющихся данных и задач, стоящих перед бизнесом (табл. 2).
рированных кредитов как «хороших», а для получения более точного прогноза использовать методы, учитывающие недожившие кредиты, – метод взвешивания цензурированных данных и метод Каплана – Мейера.
Заключение
В данной работе было произведено исследование влияния цензурированных данных на оценку калибровочного коэффициента скоринговой модели, рассчитанного на основе трех методов, – линейной калибровки от значений вероятностей, линейной калибровки от значений шансов, логарифмической калибровки от значений шансов. Проблему несоответствия прогнозного значения числа дефолтов по модели кредитного скоринга с фактическими данны- ми возможно устранить с учетом цензурированных данных, применяя одну из указанных методик, а именно: учет цензурированных кредитов как «хороших», исключение цензурированных кредитов из выборки, метод Каплана – Мейера, метод взвешивания. Данные методы учета цензурированных данных позволяют более корректно рассчитывать долю дефолта и мо- либровке банковской модели кредитного скоринга. Однако выбор метода учета цензурированных данных будет зависеть от политики кредитной организации: для организаций с низким уровнем риск-аппетита необходимо использовать метод исключения цензурированных кредитов, для организаций с высоким уровнем риск-аппетита ‒ учитывать цензурированные кредиты как «хорошие», а для получения более точного прогноза при адекватном риск-аппетите использовать методы взвешивания цензурированных данных и Каплана – Мейера. Дальнейший интерес к проблеме заключается в учете цензурированных данных не только на этапе валидации скоринговой модели, но и на первоначальном этапе ее построения [15–18], а также определение размера экономического капитала на покрытие непредвиденных потерь по портфелю потребительских кредитов [19–20].
гут равноправно использоваться при ка-
Список литературы Калибровка скоринговой модели с учетом цензурированных данных
- Алескеров Ф.Т., Солодков В.М., Челнокова Д.С. Динамический анализ паттернов поведения коммерческих банков России // Экономический журнал Высшей школы экономики. 2006. Т. 10, № 1. С. 48-61.
- Алескеров Ф.Т., Белоусова В.Ю., Сердюк М.Ю., Солодков В.М. Стереотипы поведения российских банков // Банковское дело. 2008. № 7. С. 44-50.
- Алескеров Ф.Т., Андриевская И. К., Пеникас Г. И., Солодков В.М. Анализ математических моделей Базель II. 2-е изд., испр. М.: Физматлит, 2013. 295 с.
- Кудрявцева М. Идентификация значимых рисков: методические подходы и практические результаты // Риск-менеджмент в кредитной организации. 2017. № 3. С. 92-102.
- Широбокова М.А., Лётчиков А.В. Сравнение методов калибровки скоринговой модели при прогнозировании логистической регрессией // Вестник Удмуртского университета. Серия экономика и право. 2017. № 2. С. 74-79.
- Кокс Д.Р., Оукс Д. Анализ данных типа времени жизни / пер. с англ. О.В. Селезнева. М.: Финансы и статистика, 1988. 191 с.
- Лётчиков А.В., Матвеев Р.Ю., Широбокова М.А. Решение проблемы цензурированных данных при моделировании оценки индивидуального кредитного риска // Вестник Удмуртского университета. Серия экономика и право. 2019. № 1. С. 34-41.
- Груздев А.В. Прогнозное моделирование в IBM SPSS Statistics, R и Python: метод деревьев решений и случайный лес. М.: ДМК Пресс, 2018. 642 с.
- Банных А.А., Лётчиков А.В. Методика оценки кредитного риска заемщика с применением скоринга бюро кредитных историй // Вестник Удмуртского университета. Серия экономика и право. 2013. № 4. С. 5-9.
- Банных А.А., Лётчиков А.В. Методика расчета экономического капитала на покрытие непредвиденных потерь по портфелю потребительских кредитов // Вестник Удмуртского университета. Серия экономика и право. 2015. № 1. С. 18-24.
- Лётчиков А.В. Расчет индивидуального кредитного риска с применением модели геометрического распределения // Вестник Удмуртского университета. Серия экономика и право. 2018. № 2. С. 208-213.
- Dirick L., Claeskens G., Baesens B. Time to default in credit scoring using survival analysis: A benchmark study // Journal of the Operational Research Society. 2017. Vol. 68, Iss. 6. P. 652-665.
- Kaplan E.L., Meier P. Nonparametric estimation from incomplete observations // Journal of the American Statistical Association. 1958. Vol. 53, № 282. Р. 457-481.
- Diez D. Survival analysis in R. URL: https://folk.ntnu.no/bo/TMA4275/Download/R.tutorialDiez.pdf. (дата обращения: 31.05.2019).
- Ishwaran H. The effect of splitting on random forests // Machine Learning. 2015. Vol. 99, № 1. P. 75-118.
- DOI: 10.1007/s10994-014-5451-2
- Mogensen U.B., Ishwaran H., Gerds T.A. Evaluating random forests for survival analysis using prediction error curves. University of Copenhagen, 2012. URL: https://ifsv.sund.ku.dk/biostat/annualreport/images/4/4d/Research_Report_10-8.pdf (дата обращения: 31.05.2019).
- Man R. Survival analysis in credit scoring: A framework for PD estimation. University of Twente, 2014. URL: https://pdfs.semanticscholar.org/b4e3/ee5a66e180ba6d3cc7174ee232799cfd1831.pdf (дата обращения: 31.05.2019).
- Широбокова М.А. Модель оценки риска дефолта на всем протяжении жизни кредита // Вестник Удмуртского университета. Серия экономика и право. 2018. № 2. С. 228-233.
- Philosophov L. Assessing validity and accuracy of the Basel II Model in measuring credit risks of individual borrowers and credit portfolios // SSRN Electronic Journal. 2012.
- DOI: 10.2139/ssrn.655205
- Лётчиков А.В., Маркова А.А. Прогнозная оценка убытков по кредитному портфелю на основе миграционной модели // Математические методы и интеллектуальные системы в экономике и образовании: материалы всеросс. заоч. науч.-практ. конф. Ижевск: Изд-во ИЭиУ УдГУ, 2015. С. 10-12.


