Калибровочный подход в теории тяготения, физическое пространство-время и гравитационное взаимодействие

Введение. О гравитационном взаимодействии в общей теории относительности

Создание теории относительности привело к радикальным изменениям существовавших представлений о физическом пространстве и времени и преобразило всю физику XX века. Согласно теории относительности 3-мерное пространство и время образуют 4-мерный континуум. В рамках специальной теории относительности это псевдо-евклидов мир Минковского. Согласно общей теории относительности (ОТО) учет гравитационного взаимодействия приводит к более сложным метрическим свойствам физического пространства-времени, образующего 4-мерный псевдо-риманов континуум. ОТО, лежащая в основе теории гравитации, релятивистской космологии и астрофизики, дает адекватное описание различного рода систем и физических явлений в астрофизике и астрономии, включая наблюдаемую Вселенную как целое. В то же время ОТО сталкивается с некоторыми принципиальными трудностями, появляющимися в определенных условиях при описании гравитирующих систем.

Гравитационное поле, описываемое в ОТО с помощью метрического тензора физического пространства-времени на основе уравнений тяготения Эйнштейна, имеет в качестве своего источника тензор энергии-импульса гравитирующей материи. В случае обычной материи с положительными значениями плотности энергии и давления, удовлетворяющей условию энергодоминантности, гравитационное взаимодействие в рамках ОТО имеет характер притяжения, увеличивающегося с ростом плотности энергии. В конечном итоге это и является причиной появления сингулярных состояний в космологических моделях Большого Взрыва и черных дыр. Наличие в начале стадии расширения в различного рода космологических моделях сингулярного состояния с расходящейся плотностью энергии и сингулярной метрикой ведет к проблеме начала Вселенной во времени - проблеме космологической сингулярности (ПКС). Следует заметить, что хотя в рамках ОТО гравитационное взаимодействие может иметь характер отталкивания в случае гравитирующей материи с отрицательным давлением (например, скалярные поля в инфляционных моделях), ПКС не может быть решена в ОТО на основе рассмотрения таких систем: несмотря на появление некоторых регулярных решений, большинство космологических моделей остаются сингулярными.

Другая принципиальная проблема ОТО связана с введением темных составляющих материи с целью объяснения наблюдательных космологических и астрофизических данных. Их объяснение в рамках ОТО приводит к выводу, что около 96% энергии во Вселенной связано с некоторыми гипотетическими видами материи - темной энергией и темной материей, а вклад в энергию обычной барионовой материи составляет лишь около 4%. В то время как темная энергия была введена сравнительно недавно с целью объяснения открытого ускоренного космологического расширения в современную эпоху, понятие темной материи, введенной для объяснения наблюдательных данных, относящихся к движению объектов в галактиках и скоплениях галактик, известно уже более 70 лет.

В результате нынешняя ситуация в космологии и в целом в теории гравитации подобна ситуации, сложившейся в физике в начале XX века, когда было введено понятие эфира с целью объяснения различного рода электромагнитных явлений. Как известно, создание специальной теории относительности позволило решить соответствующие проблемы без использования понятия эфира.

Предпринималось множество попыток с целью решения указанных выше космологических проблем как в рамках ОТО и существующих теорий, претендующих на роль квантовой теории гравитации - теории струн/М-теории и петлевой квантовой теории гравитации, так и различных обобщений Эйнштейновской теории тяготения (см. напр. [1, 2]). Радикальные идеи, связанные с такими понятиями, как струны, дополнительные пространственные измерения, квантование пространства-времени и т.д., использовались в этих работах. Различные гипотетические поля и частицы с необычными свойствами как возможные кандидаты, претендующие на роль темной энергии и темной материи, обсуждались в литературе. Следует при этом заметить, что многие обобщения Эйнштейновской теории тяготения базируются на вводимых ad hoc гипотезах и не имеют под собой солидной теоретической базы.

В то же время существует теория тяготения, построенная на основе общепринятых теоретикополевых принципов, включая принцип локальной калибровочной инвариатности, являющаяся естественным обобщением ОТО и открывающая возможности для решения ее принципиальных проблем. Это Пуанкаре калибровочная теория тяготения (ПКТТ) - теория тяготения в 4-мерном физическом пространстве-времени, имеющем структуру континуума Римаиа-Картаиа U4. Становление ПКТТ неразрывно связано с пионерскими работами [3-5] (см. [6] и цитированную там литературу). С точки зрения калибровочного подхода, ПКТТ является необходимым обобщением ОТО, если группа Лоренца (группа тетрадных лоренцевых преобразований) входит в состав калибровочной группы, соответствующей гравитационному взаимодействию. ПКТТ приводит к существенным изменениям в структуре физического пространства-времени и характера гравитационного взаимодействия при определенных условиях в гравитирующих системах.

Данная работа посвящена обсуждению физических следствий, полученных в рамках ПКТТ при исследовании космологических проблем и связанных с характерными отличиями гравитационного взаимодействия в определенных условиях по сравнению с ОТО, позволяющими преодолеть соответствующие трудности ОТО. Предварительно в п. 2 дается изложение некоторых положений калибровочного подхода в теории тяготения в связи с обсуждением того места, которое занимает ПКТТ в рамках данного подхода.

1.    Калибровочный подход в теории тяготения и ПКТТ

Принцип локальной калибровочной инвариантности лежит в основе современной теории фундаментальных физических взаимодействий. В рамках калибровочного подхода была построена стандартная модель теории электрослабого и сильного взаимодействий. Принцип локальной калибровочной инвариантности устанавливает глубокую связь между важнейшими сохраняющимися величинами, существование которых связано согласно теореме Нетер с инвариантностью теории относительно соответствующих групп преобразований, и фундаментальными (калибровочными) физическими полями, имеющими в качестве источников соответствующие сохраняющиеся величины и выступающими в качестве носителей определенных физических взаимодействий. В соответствии с теорией Янга-Миллса схема введения калибровочных полей прозрачна и не вызывает никаких вопросов в случае групп внутренней симметрии в пространстве Минковского, рассматриваемых в теории электрослабого и сильного взаимодействий. Ситуация меняется при переходе к гравитационному взаимодействию, в случае которого калибровочная группа оказывается связанной с координатными преобразованиями и в процессе локализации группы меняется геометрическая структура пространства-времени. На самом деле, если тензор энергии-импульса рассматривать как источник поля тяготения (именно такова ситуация в метрической теории тяготения), гравитационное взаимодействие следует вводить на основе локализации 4-параметрической группы трансляций в пространстве Минковского, инвариантность относительно которой и приводит к введению тензора энергии-импульса и к законам сохранения энергии и импульса. Именно таким путем поле тяготения как симметричное тензорное поле 2-го ранга впервые было введено в [7]. Введенное калибровочное поле связывалось с метрическим тензором пространства-времени, имеющего структуру псевдо-риманова континуума. Таким образом, локализация 4-параметрической группы трансляций приводит к теории, ковариантной относительно общих координатных преобразований и представляющей собой метрическую теорию тяготения, которая при соответствующем выборе гравитационного лагранжиана сводится к теории тяготения Эйнштейна. В [8] поле тяготения также было введено на основе локализации 4-параметрической группы трансляций, при этом калибровочное поле представлялось как совокупность четырех векторных полей, связанных с четверкой ортонормированных тетрад; соответствующая теория представляет собой теорию тяготения в пространстве абсолютного параллелизма (телепараллелизма). Позднее поле тяготения как калибровочное поле, связанное с 4-параметрической группой трансляций, рассматривалось в работе [9].

Рассмотрим сейчас вопрос о роли группы Лоренца в теории тяготения, вводимой на основе локализации 4-параметрической группы трансляций. Речь идет о группе тетрадных лоренце-вых преобразований, не связанной с преобразованием координат и присутствующей в теории при наличии в каждой точке пространства-времени ортонормированной тетрады. Поскольку метри-ч ( ?скип тензор g^v связанный с ортопормировашюй т ( ?тра.доп hi* по (формуле g^v = Пікhi^hiv (Пік = diag (1, —1, —1, —1) - метрпческіпі т ен ： з ор прост р ан ст в а-времени N Іішковского. греческие ii латинские индексы используются для обозначения голономных и неголономных координат соответственно) инвариантен относительно тетрадных лоренцевых преобразований с произвольными параметрами, тетрадная формулировка метрической теории тяготения, получаемая в результате введения ортонормированной тетрады в каждой точке пространства-времени, инвариантна относительно локализованной группы Лоренца. Это означает, что группа тетрадных лоренцевых преобразований в рамках метрической теории тяготения не может играть динамическую роль с точки зрения калибровочного подхода. С этим связано также обращение в нуль инварианта Нетер, соответствующего группе Лоренца, в метрической теории тяготения [10]. Что же касается теории тяготения в пространстве абсолютного параллелизма, то данная теория ковариантна лишь относительно тетрадных лоренцевых преобразований с постоянными во всем пространстве параметрами и, с точки зрения калибровочного подхода, представляет собой промежуточный этап на пути построения теории, ковариантной относительно локализованной группы Лоренца. Переход к такой теории достигается благодаря введению калибровочного лоренцева поля, имеющего трансформационные свойства неголономной лоренцевой связности [11]. Трактовка данного поля как независимого динамического поля приводит к теории тяготения в пространстве Римана-Картана, известной в литературе как Пуанкаре калибровочная теория тяготения.

Примечательно, что впервые попытка трактовки гравитационного взаимодействия на основе принципа локальной калибровочной инвариантности была предпринята Р. Утиямой в 1956 году вскоре после построения теории полей Янга-Миллса [11]. В качестве калибровочной группы при этом рассматривалась группа Лоренца. Утияма ввел калибровочное лоренцево поле, и поскольку трансформационные свойства неголономной лоренцевой связности одинаковы в пространстве Римана и в пространстве Римана-Картана, Утияма смог получить гравитационные уравнения Эйнштейна, отождествляя калибровочное лоренцево поле с коэффициентами вращения Риччи риманова пространства. Однако, как было отмечено в [3], подобное отождествление не допустимо, если калибровочное лоренцево поле трактовать как независимое динамическое поле. Кроме того, трактовка поля тяготения как калибровочного поля, соответствующего группе Лоренца, не последовательна, если принять во внимание соответствие между калибровочными полями и их источниками (см. выше).

Принципиальная значимость ПКТТ в рамках калибровочного подхода в теории гравитационного взаимодействия определяется той ролью, которую играет группа Лоренца в современной физике. Инвариантрость теории относительно группы тетрадных лоренцевых преобразований фактически означает, что локально метрические свойства физического пространства-времени такие же, как и пространства-времени Минковского. Помимо метрических свойств физическое пространство-время обладает свойствами, связанными с наличием кручения у лоренцевой связности, выступающей как фундаментальное физическое поле. Совместно с тетрадой hi* ііеголомная лоренцева связность Aik* = —Aki* 口гратот роль ііезашісіімнх переметших поля тяготения. Соответствующие им напряженности - это тензоры кручения Si*v и кривизны Fik*v・ Тензор кривизны, являясь напряженностью, соответствующей группе тетрадных лоренцевых преобразований, определяется подобно напряженности калибровочного янг-миллсовского поля. В отличие от кривизны, тензор кручения, будучи напряженностью, соответствующей подгруппе пространственно-временных трансляций, является функцией не только тетрад и их производных, но также калибровочного лоренцева поля (см. ниже), что является отличительной особенностью калибровочной теории, связанной с координатными преобразованиями. Лагранжиан гравитационного поля представляет собой инвариант, построенный из тензоров кривизны и кручения (а также тетрады или метри- ки). В случае минимальной связи материи с гравитационным полем, определяемой с помощью замены в лагранжиане материи, записанном в пространстве Минковского (в прямоугольной декартовой системе координат инерциальной системы отсчета), частных производных материальных переменных на ковариантные производные, определяемые с помощью полной связности пространства Римана-Картана, в роли источников поля тяготения в гравитационных уравнениях ПКТТ выступают тензор энергии-импульса и тензор спинового момента гравитирующей материи. Простейшая ПКТТ - теория Эйнштейна-Картана - соответствует выбору гравитационного лагранжиана в виде скалярной кривизны пространства-времени U4. Большой вклад в исследование теории Эйштейна-Картана в связи с попытками решении ПКС был внесен польскими физиками [12]. В случае бесспиновой материи гравитационные уравнения теории Эйнштейна-Картана сводятся к уравнениям тяготения Эйнштейна, в случае материи со спином теория Эйнштейна-Картана приводит к линейной связи между кручением пространства-времени и спиновым моментом. Данное обстоятельство послужило причиной широко распространенного в литературе мнения, что кручение порождается спином, а в случае бесспиновой материи должно исчезать. В действительности же данное обстоятельство скорее свидетельствует о вырожденном характере теории Эйштейна-Картана, если учесть, что тензор кручения представляет собой напряженность поля тяготения, соответствующую подгруппе пространственно-временных трансляций и непосредственно связанную с тензором энергии-импульса гравитирующей материи. При включении в гравитационный лагранжиан ПКТТ, подобно теории Янга-Миллса, квадратичных относительно напряженностей инвариантов ситуация нормализуется, и ПКТТ представляет собой теорию тяготения, в рамках которой гравитационное поле описывается посредством взаимодействующих между собой метрики и кручения, источниками которого являются тензор энергии-импульса и тензор спинового момента гравитирующей материи.

Существуют различного рода возможности обобщения ПКТТ, связанные с рассмотрением вместо группы Лоренца других более общих групп, - конформная калибровочная теория, (анти-) де-Ситтеровская калибровочная теория (см. [6] и цитированную там литературу). Весьма общая теория -это аффинно-метрическая калибровочная теория тяготения, в рамках которой связность обладает наряду с кручением также и неметричностью. При соответствующих ограничениях немет-ричности имеет место теория в пространстве Вейля-Картана. По сравнению с указанными выше теоретически возможными построениями калибровочной теории тяготения принципиальная значимость ПКТТ определяется фундаментальной ролью группы Лоренца в физике, и прежде всего в теории фундаментальных физических взаимодействий.

2.    Кручение физического пространства-времени и гравитационное взаимодействие

ПКТТ базируется на выборе гравитационного лагранжиана Lg, представляющем собой инвариантную функцию, построенную из напряженностей поля тяготения - тензоров кручения и кривизны, определяемых следующим образом

Si“v = d[v h%- hk[“Aikv],

F^ik“v = 2д [』] +2А“^к |i |v ]

Поскольку в пространстве U4 можно построить ряд инвариантов, квадратичных по кривизне и кручению, мы будем использовать достаточно общее выражение Lg, содержащее помимо скалярной кривизны всевозможные квадратичные инварианты с неопределенными параметрами, предполагающие сохранение пространственной четности

Lg = fo F + F " 加( fl Fae“v + f2 F a"Bv + /з Ғ “〃 ав) +F"" (/4 F“v + /5 F 〃“ ) + /6 F²

+Sa"V (ai Sa“v + a2 Sv“a) + аз Sa“aSe"e, (2.1)

rje F 停 V = F^a_Mav- F = F 丛小 f i (i = 1,2,..., 6). ak (k = 1,2, 3) - ііеопределеішые параметры. /0 = (16nG)^-1. G - ііьтотоповская гра.вігтатіііоішая постоянная (скорость света в вакууме c = 1). Гравитационные уравнения, вводимые на основе интеграла действия I = f (Lg + Lm) hd⁴x, где h = det (һ/) ii Lm - лагранжиан гра.вптпрутс ) ш ( ?п мат ( ?ріш. содержат систему 16—24 ура.вііеішп. соответствующих гравитационным переменным hi* и Aik/

▽ “U 严 + 2S^kivUk"^v + 2(fo + 2f6 F)F",

+4fi FkiimFkl"m + 4f2 Fk[m"]lFkiim

+4f3 F"klmFlmik + 2f4 ( FkiF^k" + F"kimF^km)

+2f5 ( FkiF"^k + F"kimF^mk) - hi"Lg = -Ti",                         (2.2)

4Vv [(fo + 2f6 F)h[ivhk]" + f Fikv"

+f2 F[i[vk]"] + f3 Fv"ik + f4 F[k ["hi]v] +

+f5 F["[khi]v]] + U[ik]" = J[ik]",                                     (2-3)

где Ui"v = 2(ai Si"v - a? S["v], - аз Saa["hiV]). Ti" = -h1 fLm^ J[ik]" = -h1 3ALm^ V” означает ковариантный оператор, имеющий структуру ковариантной производной, определяемой в случае голоііомііых тензорных индексов с помощью коэффициентов Кристоффеля ｛入｝, а в случае тет-µν радных тензорных индексов - с помощью ііеголоііомпой лоренцевой связности Aikv (например, Vvhi" = dv hi" - ｛：〃｝ hix - Aikvhk").

Гравитационные уравнения (2.2)-(2.3) представляют собой сложную систему дифференциальных уравнений в частных производных с неопределенными параметрами. Данная система уравнений существенно упрощается в случае гравитирующих систем, обладающих высокой степенью симметрии, при этом уменьшается зависимость от неопределенных параметров. Так, в случае пространственно однородных изотропных моделей (ОИМ), исследуемых в рамках изотропной космологии, система гравитационных уравнений сводится к системе четырех уравнений для определяющих характеристик системы - масштабного фактора метрики Робертсона-Уолкера R(t) и двух функций кручения Si(t) и S?(t), определяющих неисчезающие компоненты тензора кручения ОИМ (в отличие от Si (функция S? имеет пс ( ?вдоскалярпып характер относительно преобразоватшіі пространственных инверсий) [13]. Неисчезающие компоненты тензора кривизны при этом выражаются через следующие четыре функции Ai (i = 1,2, 3,4)

Ai = H + H² - 2HSi - 2si, k

A2 = R2 ^{+ (H} - 2S1 ) - S2 ,

Аз = 2(H - 2Si) S2,

A4 = S 2 + HS2,                               (2.4)

где? H = R /R -параметр Хаббла, k = 0, -1, +1 для пространственно плоских, гиперболических и сферических моделей соответственно, а точка означает дифференцирование по времени.

Система гравитационных уравнений для ОИМ позволяет получить космологические уравнения, обобщающие фридмановские космологические уравнения ОТО, а также уравнения для функций кручения, которые в общем случае зависят от следующих пяти неопределенных параметров:

а = 2。1 +。2 + 3аз,     b =a2 —a1, f2 f = f1 + "2 + f3 + f4 + f5 + 3f6 , qi = f2 - 2f3 + f4 + f5 + 6f6,     q2 = 2fi - f2.

Математическая структура получаемых уравнений, лежащих в основе изотропной космологии, и их физические следствия существенно зависят от ограничений, накладываемых на эти параметры. Данные уравнения исследовались при различных ограничениях на неопределенные параметры [13-19]. Как было показано в [18], наиболее удовлетворительные как с математической, так и физической точки зрения результаты имеют место при следующих ограничениях: а = 0, q2 = 0. Первое ограничение приводит к отсутствию высших производных от масштабного фактора в космологических уравнениях [20], а второе приводит к принципиальному физическому выводу о возможном существовании предельной плотности энергии для гравитирующих систем в случае рассматриваемых ОИМ с двумя функциями кручения. Ниже будет рассматриваться изотропная космология, построенная в рамках ПКТТ при указанных ограничениях на неопределенные параметры. Уравнения изотропной космологии при этом зависят от следующих трех параметров: параметра a = 3f2 > 0. имспошего ра：зм(?рпость. обратиуто ра：зм(?рпостіі плотности эіі(?ргіш. параметра b с такой же размерностью, как и fo, а также безразмериого параметра ® = 2ffq1. Космологические уравнения имеют следующий вид:

炉 + (H - 2Si)2 - S2 = 6 f_oz [ p - ^6bS2 + 4 ( p - 3p - 12b^S2 )[ ,

(2-5)

1 12foZ

H + H² - 2Hs_i - 2s 1 = [^{p + 3p} - 2 (p - ³p - ^12bS2 ) ²] ,

(2.6)

rje p - плотность 'Әпергіш. p - давление гра.вптпрутс ) ш ( ?п мат ( ?ріш. a Z = 1 + a (p - 3p - 12bS2). Функция кручения Si определяется следующим образом:

α

Si = - —；- [p — 3p + 12/о®Н$2 - 12(2b - ®fo)S2s2],                      (2 」,)

а функция кручения S2 является функцией плотности энергии p и давления p и определяется по формуле

p - 3p I 1 - (b/2fo)(1 + 衣 ) 12b ⁺    12ba(1 - ^/4)

⑵ 8)

где X = 1+ ^(f2/b2)[1 - (b/fo) - 2(1 - ^/4)a(p + 3p)].

Материальное содержание космологических ОИМ, а также уравнение состояния гравитирующей материи меняются по мере их эволюции, вид уравнения состояния при этом зависит от связи гравитирующей материи с полем тяготения. Для построения инфляционных космологических моделей будем полагать, что на начальных этапах космологического расширения, помимо обычной материи с плотностью энергии pm > 0 и давлением pm > 0, ОИМ содержат также в качестве материальной компоненты скалярное поле ф с потенциалом V = V (ф). В случае минимальной связи с

полем тяготения характеристики материальных компонент удовлетворяют таким же уравнениям, как и в ОТО:

0m + 3^{H (p}m + pm) = 0, ∂V 而 + 3 血 = -林.

(2-9)

⑵ 10)

Выражения для полной плотности энергии p и давления p в уравнениях (2.5)-(2.8) имеют вид:

p = 2ф + V + pm  (p > 0), p = 2ф - V + pm.

(2.11)

Прежде чем переходить к рассмотрению важнейших следствий изотропной космологии представим выражение (2.7) для функции кручения Si, получаемое с помощью соотношений (2.8)-(2.11) в виде

^Si = - 當( HD + E ) ,

⑵ 12)

где

D =5 ( 3^m - ] ) (pm + pm) 2 \ dpm    丿

⁺ 3 ^(pm - ^{3pm) +} 3^{ф2 +} 3V - 6foa(1b- 3/4) A +^1- 2^f/^2b) [( ³ dpm⁺¹ 卜 ^pm+p^m)+^{4ф 2} ]

. 1 - (b/2fo) 3a(1 — з/4) ，

E = ( 1 + — )沙

-3/4+(b/2fo)(1 + VX)

=----------------------------_

⑵ 13)

Как было показано в [18], наиболее важные физические следствия имеют место, если безразмерный параметр ® положителен и достаточно мал 0 < ® 《 1. В данном случае космологические уравнения ведут к космологическим решениям, описывающим в асимптотике, где плотность энергии достаточно мала, ускоренно расширяющуюся Вселенную, регулярную в начале космологического расширения. Обсудим данные физические результаты более подробно.

• а)    Космологическое ускорение в современную эпоху как вакуумный эффект.

В силу 0 < ®《1 в асимптотике. где1 плотность 'Әпергіш достаточно мала, справедливы следующие ограничения X т 1, Z т *, Si т 0 и функция кручения S2 приближенно равна р — 3p + 1 — b/fo 12b 十 12ab

(2.14)

В результате космологические уравнения (2.5)-(2.6) принимают вид космологических уравнений Фридмана с эффективной космологической постоянной, индуцируемой функцией кручения

R + H² = fo 卜 fo/b) + 4a-Y^{1 —} b/.^f0 ) ²(.^fo/^b)] ,                   ( 215)

H + H² = — ₁f 0 卜 P + 3p)(fo/b) — 2a^-1(1 — b/fo)²fo/b)] .              (2.1G)

При определенном соотношении между параметрами a и b эффективная космологическая постоянная в уравнениях (2.15)-(2.16) совпадает со значением космологической постоянной, принимаемой в ОТО, и эти уравнения для пространственно плоской модели (k = 0) совпадают с уравнениями стандартной ACDM-модели, если значение слагаемого p(fo/b) в правой части уравнения (2.15) равняется сумме плотности энергии барионовой и темной материи. Тогда соответствующие решения описывают поведение ускоренно расширяющейся Вселенной в полном соответствии с Л CDM- моде ль то. Зиачепне параметра b определяет вклад темпон материи в плотность 'Әпергіш р. Принимая во віііімашк? ту роль, которую играет темная материя в астро(])口знк已 замет1nL что решение проблемы темной материи предполагает исследование систем, неоднородных в астрофизических масштабах. Если темная материя существует, значение b чрезвычайно близко к значению /о，оставаясь меньше /о，при зтом величина a-1 соответствует шкале высоких плотностей знер-гии. Как было показано в [17], физическое пространство-время в вакууме в случае обсуждаемых космологических ОИМ в ПКТТ имеет структуру пространства-времени де Ситтера с неисчезающим кручением (без введения в теорию космологической постоянной), в результате чего вакуум в ПКТТ приобретает динамические свойства, а наблюдаемое ускоренное космологическое расшире ние в современную эпоху - вакуумное происхождение.

• б)    Предельная плотность энергии и гравитационное отталкивание в экстремальных условиях.

Космологические уравнения (2.5)-(2.6) ведут к принципиальным следствиям в поведении ОИМ в начале космологического расширения в экстремальных условиях (экстремально большие плотности энергии и давления). В случае положительных параметров ^ и a из условия неотрицательности X следует ограничение для допустимых значений плотности энергии и давления

X = 1+ 3(/2/b²)[1 — (b//o) — 2(1 — 3/4)a(p + 3p)] >  0 (2.17)

В случае ОИМ, заполненных обычной гравитирующей материей с плотностью энергии pm (pm = pm(pm)) без скаляр i іых полей J ) ав он ( ? тво. ： з а.да.в аг? м ос по ср с\л, ( ? твом (2.17). определяет предельную, т.е. максимально допустимую плотность энергии p_max, имеющую порядок величины (®a)^-1. В рамках рассматриваемой классической теории величина pmax должна быть меньше плаиковской плотности энергии. Вблизи предельной плотности энергии гравитационное взаимодействие имеет характер отталкивания, обеспечивая регулярное поведение ОИМ относительно плотности энергии, пространственно-временной метрики и параметра Хаббла. В случае моделей, включающих на начальной стадии расширения скалярные поля условие (2.17) определяет область допустимых значений материальных параметров (pm, ф, ф), ограниченную в пространстве этих параметров поверх-тюс 工 ъто L. определяемой равенством (2.17). Наличие данной поверхности обеспечивает регулярное поведение соответствующих ОИМ, включая инфляционные космологические модели. Исследуем поведение ОИМ вблизи предельной плотности энергии или поверхности L (X << 1), используя космологическое уравнение (2.5), приводящее к следующему выражению для параметра Хаббла:

H ± = — fFE 土 (fž[p + ⁶ ( ^f0Z - ^{b ) S} 2

[1 - (b/2f0)(1 + 衣 )]² [— _£丫/ 2 厶 3f03a 「 1 4a(1 - з/4)²      」 R² 丿    〈十 2bZ   丿

⑵ 18)

С учетом выражений D и E, при малых значениях X параметр Хаббла (2.18) может быть представлен в виде разложения по VX

H 土 = Hl(1 + kl Vx + k2X + кзХ^3/2 + … )，                      (2.19)

где

______ ^-2 器 ^ф ______ (3 dPm + 1)(Pm + Рт)+4ф²

(2.20)

а коэффициенты k,(i = 1,2,...) в разложении (2.19) являются функциями материальных параметров (pm, ф, ф). определяемых из (2.18). В случае 01 INI без скалярных полей Hl = 0. 11 H-- 11 H+-решения описывают стадии сжатия и расширения соответственно, переход от сжатия к расширению (так называемый бауис) происходит при достижении предельной плотности энергии (X = 0). С учетом малости параметра з, а также с учетом того, что вблизи бауиса выполняются условия a^-1 《 p. X 《 1- p 〜 (за)^-1, легко получить в лпиепиом приближении по XX следутотттее значение параметра Хаббла [18]

2b² 衣 [(1/4b)(pm + Pm) - (k/R²)]¹/² H± = ±~ ； 7S--3----------------------

(2.21)

(2.22)

^3f23^a     (3 狰 + 1)(pm + Pm)

ρm

В результате временная производная параметра Хаббла при баунсе равна

4b² (1/4b)(pm + Pm) - (k/R²)

3f23a  (3 dpm + 1)(pm + Pm)

ρm

В случае инфляционных моделей со скалярным полем переход от Н--решения к H+-решению происходит при достижении L-поверхности, на которой параметр Хаббла определяется согласно (2.20). Баунс в данном случае происходит при достижении экстремальной поверхности, получаемой из космологического уравнения (2.5), в котором следует положить H = 0. Подобно инфляционным космологическим моделям, исследованным в рамках ПКТТ в случае ОИМ с одной функцией кручения Si [21-23]. в ра.ссма.трііва.емсш случае О ИМ с двумя (функциями кручения космологические решения могут быть получены с помощью численного интегрирования системы уравнений (2.6), (2.9), (2.10) при задании начальных условий для (pm, ф, ф) на экстремальной поверхности (предполагается, что уравнение состояния pm = Pm(pm) и вид потенциала V известны). Если начальное значение скалярного поля достаточно велико, космологическое решение включает стадию перехода от сжатия к расширению, инфляционную стадию с медленно убывающими скалярным полем и параметром Хаббла и пост-инфляционную стадию с осциллирующим скалярным полем. Значения предельной плотности энергии, возникающей для каждого космологического решения, при этом являются разными для разных решений.

Примечательной особенностью изотропной космологии, построенной в рамках ПКТТ на основе ОИМ с двумя функциями кручения, является ее полная регулярность. Все космологические решения регулярны не только по метрике с ее производными (параметр Хаббла с его производной по времени), но также относительно кручения и кривизны. Действительно, функция кручения S2- являтошаяся (функцией материальных параметров, непрерывна с ее проігзводіюп по времени п регулярна благодаря существованию предельной плотности энергии. Что касается функции кручения Si. ситуация оказывается более ело?киоп. Хотя выражения (2.13) для D ii E. определятошпе ( J)yiiKTuiTO Si согласно (2.12). содержат сш іг ул яр ііые от но сит е лыю X члены, однако, используя разложение (2.19) для параметра Хаббла вблизи поверхности L (либо вблизи предельной плотности энергии), можно убедиться в том, что все сингулярные члены взаимно компенсируются, а функция

Si не расходится п при приближении к поверхности L со стороны H+- ii H—-peineiiiin определяется по формуле

2 H L 干 2

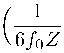
[р + 6(f o Z - b)s 2

S1

(1 - b/2f o ) ² — _kу/ ²

(2.23)

+ 4a(1 - ®/4)2 ]   R2 丿 где в выражениях для S2 и Z, определяемых по формулам (2.8) и (2.13), необходимо положить X = 0- а полная плотность 'Әпергіш р п давление p определятотся согласно (2.11). Из (2.23) следует, что в отличие от непрерывного параметра Хаббла функция Si испытывает конечный скачок на поверхности L* однако, выражеипе (H - 2Si)乙(})іігуріірут(:)шее в космологическом уравнении (2.5). определяющем параметр Хаббла, непрерывно. Аналогичным образом можно убедиться в отсутствии расходимости у производной Si для H-- и H+ - решений. В результате наряду с кручением оказываются регулярными функции тензора кривизны (2.4).

3.    Заключение

И селедов ания изотропной космологии, построенной в рамках ПКТТ, показывают, что данная теория приводит к принципиальным изменениям по сравнению с ОТО гравитационного взаимодействия, приобретающего в определенных условиях характер отталкивания. Эффект гравитационного отталкивания проявляется в экстремальных условиях, а также в ситуации, когда плотность энергии материи чрезвычайно мала и становится существенным вакуумный эффект гравитационного отталкивания. Изменения гравитационного взаимодействия связаны с более сложной структурой физического пространства-времени, а именно, с его кручением. Дальнейшие исследования гравитирующих систем, не обладающих столь высокой пространственной симметрией, должны показать, насколько общий характер имеют полученные результаты. Одновременно такие исследования позволят получить дополнительные ограничения на неопределенные параметры гравитационного лагранжиана.