Камерная модель хищник-жертва на кольцевом ареале

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 577.3.01(0.75)                                 

Локальные модели взаимодействующих популяций не учитывают пространственное распределение особей популяций. В экосистемах могут образоваться группировки особей, проживающие на небольших близлежащих участках экосистемы. Сами экосистемы могут быть протяженными в пространстве [1, 2]. Примерами таких территорий могут быть транспортные пути, побережья рек и озер, системы островов. Побережье озера может представлять собой кольцевой ареал, на котором живут различные виды, как на суше, так и в водной системе [3]. Линейный ареал – транспортные пути, вдоль которых распространяются различные виды. На линейном и кольцевом ареале заселение территории не является равномерным. Поэтому локальная модель для таких ареалов дает усредненные характеристики численности популяций, не объясняя неравномерность распределения особей по территории. Модель хищник-жертва на билокальном ареале была предложена в работе А. Д. Базыкина [4]. В статье рассматривается модель хищник-жертва для многокамерной системы.

Локальная модель

Модель хищник-жертва, учитывающая квадратичный рост малочисленной популяции жертвы, разработана в [4]:

— = u2(1 — u) — uv, at

dv

• -7-    = —/(a — u)v,

dt где u — численность жертвы, v — численность хищника, α и γ — положительные параметры. Положение равновесия в системе уравнений (1) реализуются в следующих случаях:

• 1.    u = 0, v = 0.

  
  

• 2.    u = 1, v = 0.

• 3.    и = a, v = a(1 — a)

Первое положение равновесия является неустойчивым [5] при любах значениях параметра a. Второе — устойчивым при a > 1, и неустойчивым при a < 1. Третье положение равновесия может реализовываться при выполнении неравенства a < 1, будет устойчивым только при a > 1/2.

При a < 1/2 все стационарные состояния (2) будут неустойчивыми. Функции u(t) и v(t) при значениях параметра a < 1/2 находятся в ограниченном фазовом пространстве, поэтому третье положение равновесия будет устойчивым по Лагранжу. Поскольку нулевая точка является неустойчивой, то при появлении у жертвы хищника могу возникать колебания численности жертвы и хищника [5]. На рисунке 1 для случая a = 0.45 показана зависимость функций u(t) и v(t) от времени. Начальная численность жертвы - u(t = 0) = 1.001a, и численность хищника - v(t = 0) = a(1 — a) приняты за малое отклонение от третьего положения равновесия. При малом возмущении третьего положения равновесия в (2) происходит потеря устойчивости и со временем начинаются периодические колебания в системе хищн

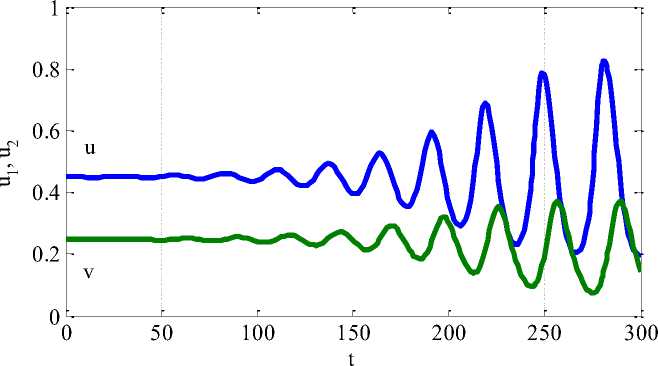
Рисунок 1. Изменение численности жертвы ( U ( t ) ) и хищника ( V ( t ) ) от времени

Камерная модель

Модель кольцевого ареала представлена последовательностью камер (зон), расположенных на замкнутой кривой единичной длины, расположенных на равных расстояниях друг от друга. Особи из одной камер могут перемещаться в любую из двух соседних. Для случая n камер модель кольцевого ареала на основе модели (1) имеет следующий вид:

du 1

— = F1(u1,v1) + cu(un

—

2u 1 + u₂),

dV,

— = F₂(u i ,V i ) + C v (V n — 2v i + v₂); где F ( u , v ) = u (1 - u ) - uv , F ( u , v ) = —у ( a — u ) v .

В модели (3) c_u параметр, характеризующий миграцию жертв в соседние камеры, а c_V - хищников. c_u и c_V считаются разными для хищников и жертв, но одинаковыми для всех камер и постоянными во времени. F 1 и F₂ - трофические функции одинаковые во всех камерах.

В модели (3) учитывается направленное движение не только хищника [6], но и жертвы. Миграция в соседние камеры считается постоянной [7] — c_V и c_u постоянные величины. Поскольку трофические функции во все камерах одинаковые, то распределение особей по камерам считается «свободным» [8] – допускается однородное распределение особей.

Система уравнений (3) имеет такие же стационарные точки, как и в случае одной камеры. При наличии миграции в системе уравнений (3) реализуется однородное положение равновесия такое, что u 1 = u₂ =... = u_n = u * и v 1 = v₂ =...= v_n = v * , где (u * v * ) одно из положений равновесия (2). При а < 1/2 третья стационарная точка системы уравнений (3) неустойчивая - в ее окрестности возникают колебания. Для п камер система уравнений (3) может содержать и другие точки притяжения такие, что распределение особей по камерам не будет однородным.

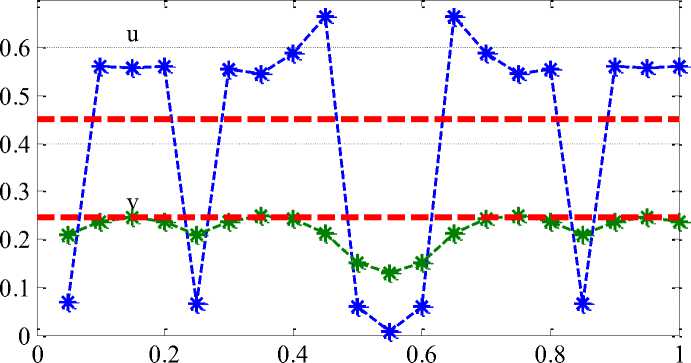
Примеры неоднородного стационарного распределения хищника и жертвы для п = 20 камер приведены на Рисунке 2 и Рисунке 3. Символом «*» отмечены численности хищника и жертвы в камерах. Значения параметров: а = 0.45, у = 0.5. Предполагается, что миграция жертвы происходит медленно (c_u = 0.01), а хищник перемещается по ареалу значительно быстрее, чем жертва: на рисунке 1 - c_V = 10c_V = 10 , на рисунке 2 - c_V = 0.7 [4]. Пунктирными горизонтальными линиями на рисунке 2 и рисунке 3 отмечены однородные решения u i = а, v t = а(1 — а) (i = 1,2,...,п).

Вариант начальных данных u1 = 0.55, u2 = u3 =... = un = 0, v1 = 0.25, v2 = v3 =... = vn = 0

предполагает, что хищник и жертва в момент времени t = 0 появляются в первой зоне с последующим распространением по остальным зонам. Колебания во всех зонах со временем прекращаются – система переходит в устойчивое неоднородное по камерам положение равновесия. При низкой подвижности хищника возможно образование множества зон с малой численностью жертвы (Рисунок 3). Интенсивное движение хищника по ареалу может привести к возникновению лишь 2-3 группировок жертвы (Рисунок 2).

При низкой подвижности хищника (при cu < 0.5) колебания в системе сохраняются, но они будут происходить около положения равновесия собственного для каждой камеры, но с одинаковой частотой для всех камер. При большем числе камер могут образовываться и боле сложные распределения по камерам значений функций. К какой из нескольких точек притяжения со времен будет стремиться решение зависит от начального приближения. Полученные результаты согласуются с данными полевых наблюдений за системой хищник – две жертвы [1].

Численное моделирование осуществлялось в среде математического пакета Matlab. Высокая скорость вычислений (несколько секунд для системы из 50 камер) достигалась за счет векторизации вычислений. Использовалась схема повышенного порядка точности для уравнений (3), разработанная в [9].

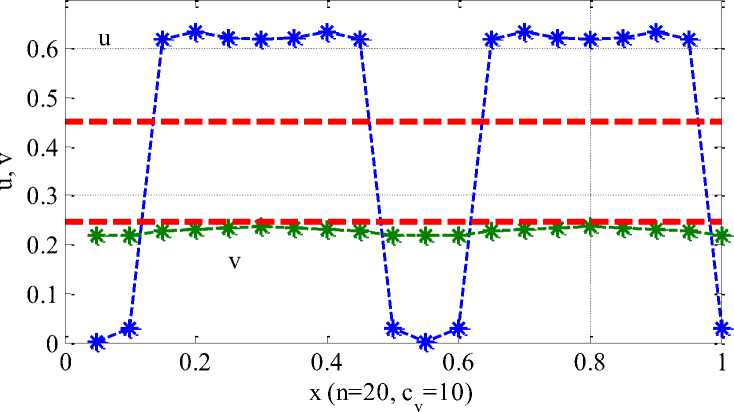
Рисунок 1. Распределение жертвы (и) и хищника (v) по 20 камерам в стационарной точке (c _v = 10)

x (n=20, c =0.7)

Рисунок 2. Распределение жертвы (и) и хищника (v) по 20 камерам в стационарной точке (c _v = 0.7)

Заключение

Камерная модель взаимодействия хищника и жертвы на линейном ареале может содержать большее число неподвижных точек, чем локальная. То есть распределение хищника, и жертвы по камерам может быть неравномерным. При высокой подвижности хищника его распределение на ареале стремится к равномерному распределению, а точка притяжения становится устойчивой. Жертва в отличие от хищника под его давлением может группироваться в отдельных зонах ареала.