Каналы с памятью и алгебраическое кодирование кодов Рида-Соломона
Автор: Лошкарев Н.Г.
Журнал: Мировая наука @science-j
Рубрика: Естественные и технические науки
Статья в выпуске: 9 (9), 2017 года.
Бесплатный доступ
Статья посвящена алгебраическому кодированию кодов Рида-Соломона. В данной статье рассматривается декодирование на основе интерполяции, которое использовано для разработки эффективного алгоритма декодирования алгоритма для решений Рид-Соломона. В центре внимания этой статьи работы представлена производительность, достигаемая в вероятностной установке, где выход канала характеризуется скорее апостериорными вероятностями, чем ошибками. Асимптотические характеристики предлагаемого алгоритма мягкого декодирования для большого числа точек интерполяции или, что то же самое, для больших списков были охарактеризованы в терминах простыми геометрическими условиями.
Кодирование, адаптация, синтез, канал связи, асимптотические характеристики
Короткий адрес: https://sciup.org/140262982
IDR: 140262982
Текст научной статьи Каналы с памятью и алгебраическое кодирование кодов Рида-Соломона
Предположим, что входной канал поступает из дистрибутива продукта и что канал без памяти. Другими словами, если X = ( x 1 ,x 2,... x n ) и Y = ( У 1 ,У 2,— Уп ) обозначают случайные векторы на канале ввода и вывода, соответственно, мы предположим, что x 1, х 2,... хп независимы и одинаково распределены, и что y зависит только от xi , что делает эти случайные величины идентичными. Эти предположения отражены в нашем определении матрицы надежности и ожидаемой оценки. Это основные понятия лежат в основе нашего алгоритма мягкого декодирования.
Хотя предыдущие предположения оправданы в разнообразии контекстов, есть важные приложения Рида-Соломона и алгебраическая геометрия, где эти предположения не являются действительными. На практике наиболее существенным из таких приложений является использование кодов Рида-Соломона (и алгебраической геометрии) как внешние коды в схемах конкатенированного кодирования [1].
В самой общей установке мы должны предположить, что канал на входе X и выходе Y управляются 2n-мерным соединением распределения вероятностей P x , у ( x , у ). Эта установка включает произвольные каналы с памятью и допускает произвольные распределения на входе канала. Для у е^ n справедливо
P ( x | у ) = P x • У ( Х , У ) (1) x | y P y ( У )
быть распределению на входе канала (x,х2,...,хи) , учитывая, что Y = у. Тогда в самом общем случае, учитывая вектор у е^n, наблюдаемый на выходе канала и q х n кратность матрицы M, нам нужно вычислить ожидаемый балл по отношению к р(• | у), а именно def
Е P„ { S M ( X ) } = Z S M ( X ) P x | y ( x | y ) = Z ( M • [ X ]) P x | y ( x | y ) . (2) x е X n X е F q
Затем нам нужно найти матрицу множественности M е M ( C ) , которая максимизирует этот ожидаемый результат. В дальнейшем мы покажем, что процедура декодирования может быть легко изменена (в оптимальный способ) для размещения каналов с памятью в общей настройке (2).
Для этого введем обобщенную матрицу надежности П * , которая сводится к матрице надежности П для каналов без памяти и распределения входных данных [3]. В общем случае n ‘ =^ ^ *J является матрицей q х n , элементы которой определяются следующим образом:
def ni, j=Pr (Xi=at\ Y=y), для i = 1,2,...,q и j = 1,2,...,n (3)
где y - наблюдаемый выход канала, X = ( xx , x2 ,..., xn ) - вход канала, a - i-й элемент входного алфавита X = F . Следующая лемма является аналогом леммы 6 для каналов с памятью и / или непродуктивными входными распределениями.
Таким образом, В является именно обобщенной матрицей надежности П * . Теореме теперь следует линейность математического ожидания
Е P„, {(M •[X ])} = (M ’ Е Pxy {[X ]}) = (M , П*) (4)
Оставшаяся проблема заключается в том, как вычислить П * данные наблюдений канала. К счастью, такие вычисления очень распространены в системах связи [5].
Учитывая совместное распределение Px , (x, y) на канале вход X и выход Y вместе со специфическим наблюдением y = (y,у2,...,уп), мы должны вычислить условные вероятности Pr (Xz = az \ Y = y) для всех ax,a2,...,aq и всех позиций j = 1,2,...,n. Это точная задача, известная как максимальное апостериорное (MAP) кодирование по символу. Общие алгоритмы для декодирования символов по символу MAP, таких как алгоритм суммарного произведения или алгоритм вперед-назад, хорошо известны [4].
В частности, если канал является конечным автоматом с умеренным числом состояний, то обобщенная матрица надежности П * может быть вычислена алгоритмом обратной связи Бахль-Коке-Елинека-Равива (BCJR) [2]. Важными особыми случаями являются каналы межсимвольной интерференции (ISI) и внешние каналы в схеме конкатенированного кодирования, память которой происходит от внутреннего блочного кода. Если решетчатая сложность внутреннего кода является умеренной (как это имеет место на практике), то алгоритм BCJR [4] обычно достаточно эффективен.
Декодирование на основе интерполяции может быть использовано для разработки эффективного декодирования алгоритма для решений Рид-Соломона. Алгоритм мягкого декодирования превосходит как GMD-декодирование, так и декодирование списка Гурусва-Судана с существенной разницей.
Асимптотические характеристики предлагаемого алгоритма мягкого декодирования для большого числа точек интерполяции или, что то же самое, для больших списков были охарактеризованы в терминах простыми геометрическими условиями. Кроме того, было показано, что асимптотические характеристики можно приближенно приблизить к размерам списка, которые ограничены константой, даже если длина кода выходит за пределы всех границ.
Таким образом, один из ключевых выводов этого раздела заключается в следующем: в контексте конкатенированного кодирования алгоритм BCJR оказывается эффективным средством для преобразования канала с памятью в канал без памяти для целей алгебраическое декодирование с мягким решением [1].
Мы отмечаем, что выигрыш в кодировании из-за алгебраического декодирования кодов Рида-Соломона по некоторым важным каналам (с памятью или без памяти) значительно превосходит соответствующие коэффициенты кодирования на канале AWGN без памяти. Например, результаты моделирования для быстрого восходящего канала Рэлея представлены на рисунке 1. Из рисунка 1(а) видно, что алгебраическое мягкое декодирование кода (255,144,112) Рида-Соломона обеспечивает коэффициент кодирования около 3,0 дБ по сравнению с декодированием с жестким разрешением, тогда как соответствующий коэффициент усиления по каналу AWGN составляет 1,5 дБ (см.рис.1). На рисунке 1 мы предполагаем, что информация о состоянии канала неизвестна получателю. Учитывая состояния канала, можно сделать еще лучше. Например, для кода Рида-Соломона (255,191,65) мы наблюдаем коэффициент кодирования мягкого решения около 2,5 дБ на рисунке 1(б), тогда как Гросс и др. [12], [13] предполагают информацию о совершенном состоянии и получают коэффициент кодирования с мягким разрешением 3,5 дБ для того же кода [5].
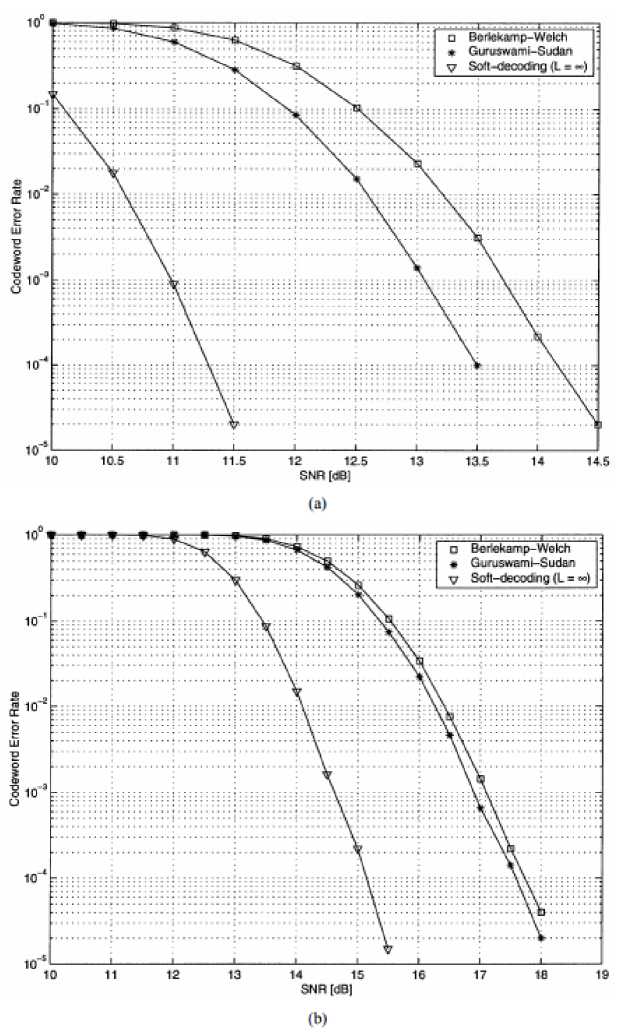
Рисунок 1. Алгебраические коэффициенты кодирования с мягким решением на быстром канале затухания Рэлея. Кодовыми словами кода Рида-Соломона являются двоичная фазовая манипуляция (BPSK), модулированный для получения последовательности 255 • S бит ( b,b 2,..., b 2040). (а) Преобразование кода Рида-Соломона (255; 144; 112). (б) Преобразование кода Рида-Соломона (255; 191; 65).
Список литературы Каналы с памятью и алгебраическое кодирование кодов Рида-Соломона
- Морелос - Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. М.: Техносфера, 2005. - 320 с.
- Гладких А.А. Основы теории мягкого декодирования избыточных кодов в стирающем канале связи. - Ульяновск: УлГТУ, 2010. - 379 с.
- Геращенко С.В. Оптимизация пространственного распределения энергетического ресурса двух РЛС и ФАР в условиях нестационарной помеховой обстановки при поиске и обнаружении целей в общей зоне обзора // Радиотехника. - 2011. -№ 10. - С. 51-57.
- Шакуров Р.Ш. Разработка и моделирование алгоритмов списочного декодирования блоковых кодов методом вычисления кластера: диссертация канд. техн. наук. - Ульяновск: УлГТУ, 2011. - 139 с.
- Ашимов, Н.М. Помехоустойчивость систем передачи информации / Н.М. Ашимов, И.В. Грачев // Электросвязь. 2009 г. - № 8. С. 45-48.


