Kernel Techniques in Support Vector Machines for Classification of Biological Data

Published Online March 2011 in MECS

Proteins are organic compounds made of amino acids and arranged in a linear chain and folded into a globular form. They are the key essential parts of an organism and exhibit a variety of roles in almost all the biological processes. It is know that some proteins are important in our human metabolism process and have important roles in both the regulation and recognition of a biological network. Others are also critical in cell signaling and cell cycles [1]. Therefore the study of the protein classification and protein function predictions are crucial for one to understand their roles in a life process.

The increasing amount of genomic and molecular information in the literature and public domains speeds up the development of efficient techniques for the analysis of protein sequence data. Protein function prediction can be viewed as a classification problem from a computer scientist’s point of view [2]. It has an important position in bioinformatics and systems biology. Various methods have been addressed to deal with the captured problem. Basically these methods can be categorized into two main classes. The first one is the generative approach. In this approach, we first build a model for each protein family utilizing positive training examples. Then we check if the test sequence fits the model or not under the given thresholds, for more details, see for instance [3], [4], [5]. The second approach is the discriminative approach. It stands as the other class that regards protein sequences as a set of labeled examples. In this approach, the difference between positive and negative training examples is modeled through a learning algorithm. One of the most successful representatives is Fisher-SVM, interested readers can consult [7], [8]. However, this method suffers from its expensive computational cost in getting the corresponding kernel matrix.

The main idea of a Kernel method is to embed data instances into a feature space F. Due to their robust performance in processing complicated data, kernel methods have shown to be effective and gained a solid footing in computational biology [14]. With the increasing popularity of the kernel-based method for pattern classification [9], a lot of string kernels have been proposed, examples are Spectrum Kernel [11], MisMatch Spectrum Kernel[12] and Kernel Based on Latent Semantic Analysis [13] etc. The Weighted Degree Kernel [20] has been applied in the recognition of alternatively spliced exons which rewards with a score on the length of the matching substrings. However, the above string kernels do not admit similarity among different features and this may result in a biased result from the physicochemical perspective. To this end, AAindex Based Kernel has recently been developed [19] in pair-wise protein homology detection. The AAindex2 [15] for amino acid similarity matrices measure the physico-chemical and biological similarities of amino acids. The similarity matrix for substrings therefore can be constructed based on the similarity matrix for the amino acids. On the other hand, motif based kernel has been demonstrated to be a powerful method in detecting remote homology [16]. Motifs usually represent functionally important regions that can be an indication for inference of the function in proteins. The information may further assist in the improvement of protein classification.

In this paper, we propose a novel kernel based on the K- Spectrum Kernel by incorporating physico-chemical and biological information in the protein sequences for the captured protein classification problem. In Section II, we present our novel approach. Numerical experiments are then given to demonstrate the superiority of the proposed method over K- Spectrum Kernel in Section III. In Section IV, we give a discussion on Eigen-matrix translation techniques. Finally, concluding remarks are given in the last section to summarize the findings and address further research issues.

• II.    T HE M ETHODOLOGY

Our new approach is based on three innovations when compared to the K- spectrum kernel. The first one is the definition of a similarity matrix among features based on the AAindex2 [17] substitution matrix. The second one is that we include the existing motif information in constructing the kernel matrix. The third innovation originates from the Positive Semi-Definite (PSD) property in the construction of kernel. The K- spectrum kernel was initially introduced followed by the novel kernel that we developed. Experiments are performed on the new kernel with SVMs on three protein data sets to demonstrate the effectiveness of our proposed kernel.

• A.    Spectrum Kernel

In the construction process of the K- Spectrum kernel, input sequences are mapped into a high-dimensional feature space. The set of all possible K- length subsequences in the protein data set constitute the feature space. We assume the protein data set contains N protein sequences

We denote the set of all K- mers existing in these N proteins by a K- mer set as follows:

Ф к ^ККфк } .

For specific p i in the data set, K- mer representation is a column vector

xK = [ xK; xК ;K xK ]'

where x_l^K_i is the occurrence of l th K- mer in the protein p i . If V K is the K- mer representation matrix for the whole protein data set which is of dimensionality n K ×N, then the K- spectrum kernel can be expressed as follows:

KerK = VT • VK K K K.

• B.    The Physico-Chemical Weighted Kernel

From the construction of the K- spectrum kernel, we observe tha t Ker K can be rewritten as follows:

KerK = VT • SK • VK K K K K.

where S K in this context is the identity matrix of dimensionality n K ×n K . In other words, the spectrum kernel assumes no similarity between two different features. However, from a physico-chemical perspective there are indeed some similarities between two different subsequences. In order to include this important information and rectify this biased hypothesis, we propose a similarity matrix between amino acids from AAindex2 where the features are fixed K- length subsequences within the protein sequences.

In the remains of this section, we first propose measurement for a pair of amino acids using the AAindex2 mutation substitution matrix. We then present the method for the construction of motif incorporated kernel. Finally, we present our Eigen-matrix translation techniques for improving the classification accuracy.

• 1)    Similarity Matrix with AAindex2 Mutation Substitution Matrix: We know that S m = MIYT790101 is an amino acid substitution matrix in protein evolution which measures the distance of a pair of amino acids. The similarity matrix for amino acids is then defined as S amino = 10 - S m . Transformation enables the similarity values to be contained in the interval [0,1] with 1 representing totally the same, 0 showing no similarity between two subjects. Given two K- mers

Ф-k = {m i, m 2 ,k mk } and

ФК ={m /, M2,K mk } the similarity between the two K-mers is defined as follows:

K

S k (Ф К , Ф К ) = П S amino ( M k , M k ).

k = 1

• 2)    The Motif Incorporated Kernel: A motif based kernel method has been shown to be significantly better when coupled to an SVM classifier when compared to a KNN classifier [16]. In constructing this kernel, the protein sequence is represented as a vector whose dimensionality is equal to the number of motifs in the database. This may give us a clue that motifs play a pivotal role in classification. We therefore measure the importance of the protein sequence in the data set according to the number of the existing motifs embedded in the sequence. We define MoWeight as follows:

MoWeight(pi) = ваПр‘ a e [0,1]

where n is the number of motifs in sequence p i . The p_i

MoWeight is a diagonal matrix of size N×N. The kernel therefore can be constructed as follows:

KerPCM = (Vq • MoWeight)T • SK • Vq • MoWeight

• 3)    The Eigen-Matrix Translation Techniques: Since the dimension of the feature space is huge, the computation error may lead to the asymmetry of the

kernel matrix. Because the asymmetric effect is not serious, we propose the following symmetrization scheme:

• (A)    Symmetrization

  Ker ^erPCM

  
  

  [ Ker_PCM + Ker_PCM ]

  
  

  TABLE I.

  3 G LYCAN S TRUCTURES

  Glycan 1	[3OSO3]Galbl=3GalNAca-Sp8
  Glycan 2	NeuAca2-3(NeuAca2-3(GalNAcb1-4)Galb1-4Glcb-Sp0)
  Glycan3	NeuAca2-8NeuAca2-8NeuAca2-8NeuAca2-3(GalNAcb1-4)Galb1-4Glcb-Sp0

  
  

Once we have the updated symmetric matrix Ker PCM , we then propose a new scheme in constructing the kernel matrix. The scheme includes an eigenvalue decomposition process (B) and an eigenvalue translation process (C).

• (B)    Eigenvalue Decomposition

KerPCM =X⋅P⋅XT where X is the orthogonal matrix containing all the column eigenvectors of the matrix KerPCM and P is the diagonal matrix containing all the corresponding eigenvalues of KerPCM, see for instance [6].

• (C)    The Eigen-matrix Translation Techniques

where λ takes value in [0.01,1].

We remark that the effect of Procedure (C) is to add a rank one PSD matrix to the kernel matrix. Generally speaking, it adds one more positive eigenvalue without making much perturbation to the original positive eigenvalues that are critical to fulfilling the classification problem. Mathematically speaking, it can be shown that if a given Hermitian matrix is modified by adding a rank one Hermitian matrix, the new and old eigenvalues must be interlacing. This can be described in the following by the Weyl' theorem for two Hermitian matrices.

Theorem 1: [6, pp. 184-185] Let A and B be two n×n Hermitian matrices and let the eigenvalues of A , B and A+B be arranged in increasing order. Then for every pair of integers j, k such that 1 ≤ j,k ≤ n and j+k ≥ n+1 , we have

λj+k-n(A+B)≤λj(A)+λk(B)

and for every pair of integers j,k such that 1 ≤ j,k≤ n and j+k ≤ n+1 , we have

That is to say if we assume

N - m

Are the eigenvalues for original Ker PCM ,

N - m - 1

are the eigenvalues for the new kernel matrix Ker PCM after performing the Eigen-matrix Translation. Then we have

TABLE II.

C LASSIFICATION R ESULT : A VERAGE AUC V ALUES

Data set	Glycan1	Glycan2	Glycan3
4-Spectrum Kernel	0.9085	0.8692	0.9270
PCM -Kernel	0.9323	0.8992	0.9630

/X                              /X                                       /X                                  /X

λ≤λ≤λ≤λL≤λ ≤λ ≤λ

1      1      2      2          m m m +1

• III.    D ATA S OURCE AND EXPERIMENTAL

• A.    Data Source

  Three sets of glycan-binding related protein data are used to evaluate the classification performance of our proposed method. Glycan structures, lectin-glycan binding affinity, lectin sequences are retrieved from the the glycan database of the Functional Glycomics Gateway (CFG) [18]. We assume a lectin binds to a glycan if the binding affinity exceeds 10000. We focus on the glycan structures with a relatively large number (≥20) of binding lectins. We finally obtained three qualified glycans and the glycan structures are illustrated in Table I.

In the captured three glycan structures, glycan-binding protein prediction can be regarded as a classification problem to assess the binding property of a protein sequence. Hence, we get three different protein datasets for the evaluation of the accuracy in classification. In Glycan 1, we have 23 positive data that is 23 protein sequences whose binding affinity are greater than 10000. In Glycan 2, we have the data set containing 22 positive data. In Glycan 3, we have the data set with 20 positive data. To ensure the balance of positive and negative data, we chose the same number of the negative data for each data set.

• B.    Experimental Results

The effectiveness of our PCM -method was evaluated through comparison with the 4-Spectrum method in terms of performance in classification. The reason for selecting 4-mer as feature is guaranteed by prior research in [11], [12] and [21] that discovered the superiority of 4-mers for string kernel. The results are shown in Table II. Fig. 1, 2 and 3 describe the performance of ten time 5-fold crossvalidation for the captured three data sets respectively. Here x- label stands for the time performing 5-fold crossvalidation and y- label is the AUC value for the classification.

We report the numerical results as follow. For Glycan1 related data set, the accuracy for 4-Spectrum Kernel is 0.9085 in average, with our developed PCM -method 0.9323; for Glycan 2 related data set, the accuracy fo4Spectrum Kernel is 0.8692 in average, with our

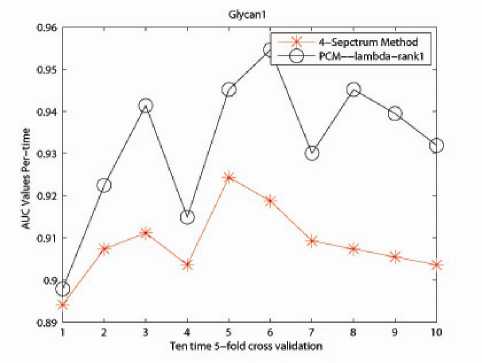
Figure 1.

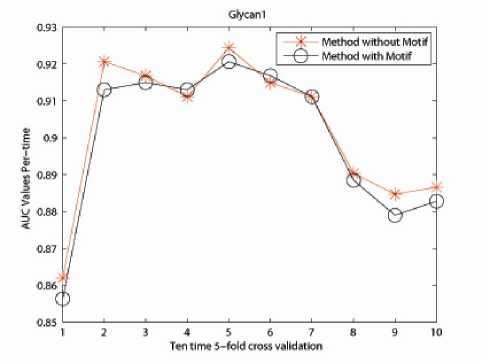
Figure 4.

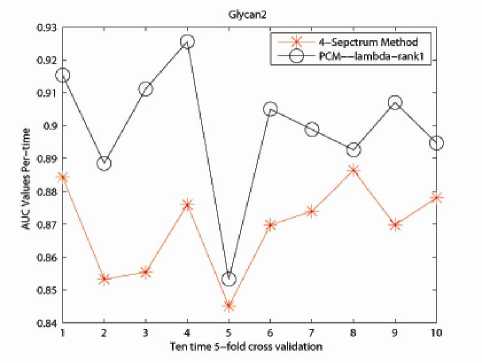
Figure 2.

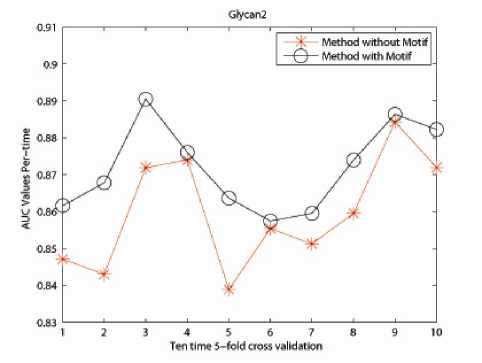
Figure 5.

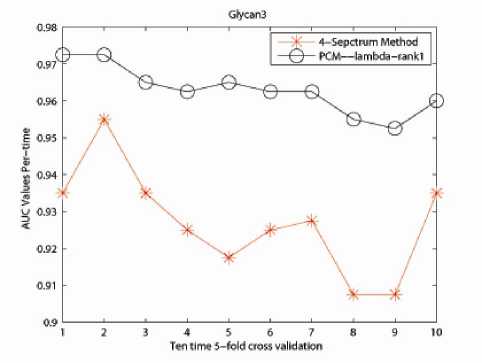
Figure 3.

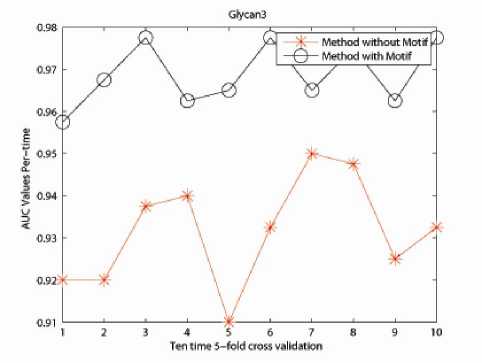
Figure 6.

developed PCM -method 0.8992; for Glycan 3 related data set, the accuracy for 4-Spectrum Kernel is 0.9270 in average, with our developed PCM -method 0.9630.

The incorporation of physico-chemical information as well as the motif information contributes a lot in improving the classification accuracy of the protein data sets. Numerical experiments demonstrate the effectiveness of our proposed method in Fig. 4, 5 and 6.

For Glycan 1 related protein data set, the method including biological information shares similar performance with 4-Spectrum Method; but for Glycan 2 and Glycan 3 related protein data sets, method taking into consideration of physico-chemical and motif information outstrips the original 4-Spectrum method. This gives us a positive indication of constructing a kernel with more biological information. However, as to the classification accuracy, there is still room for further improvement. This is also the reason of utilizing the Eigen-matrix translation technique.

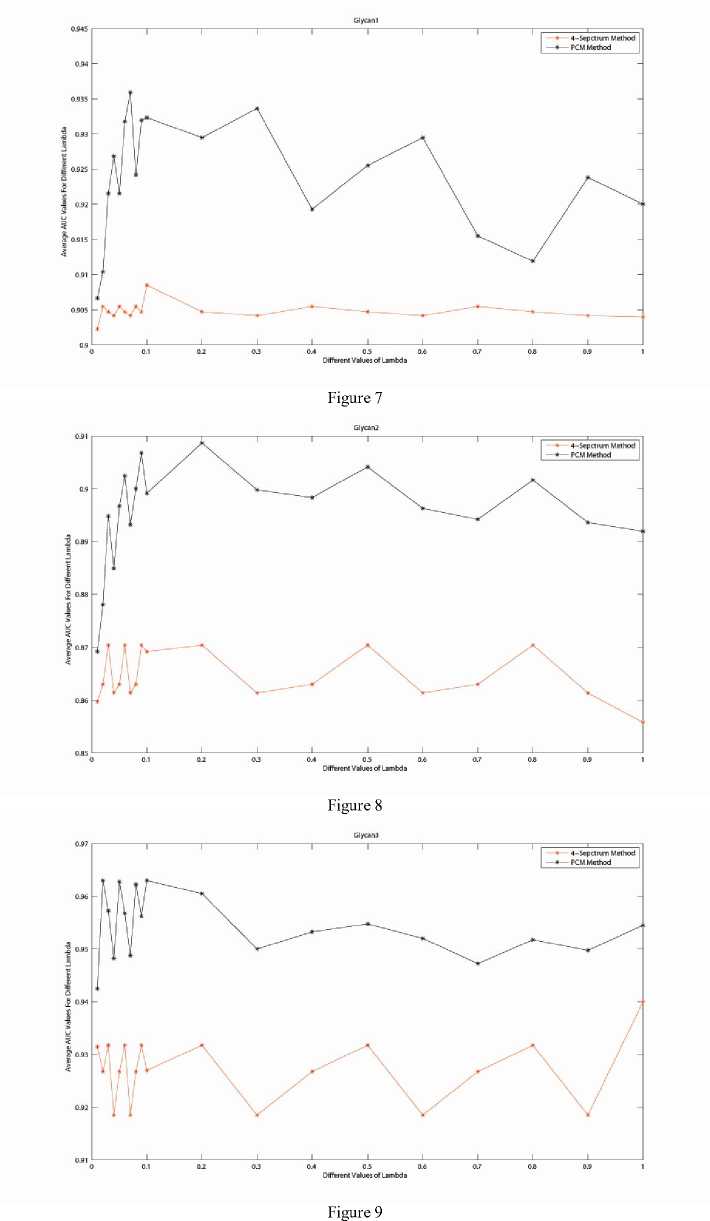
The selection of translation parameter λ is quite flexible which covers a wide range of values taking from [0.01,1]. This can be illustrated in Fig. 7, 8 and 9 which compare the classification accuracies for the three data sets subjected to different values of λ. When λ=0.1, one can achieve a better classification accuracy among all the protein data sets. Thus we adopt λ=0.1 as a favorable choice of λ in our proposed method.

Fig. 7-9 corresponds respectively to the lectin-binding protein data sets related to the three glycans in Table I. Take for example, Fig. 7 describes the classification accuracies of two methods: PCM -method and 4-Spectrum Method when λ varies from [0.01,1]. This data set is obtained from the proteins involved with

Glycan 1: [3OSO3]Galb1-3GalNAca-Sp

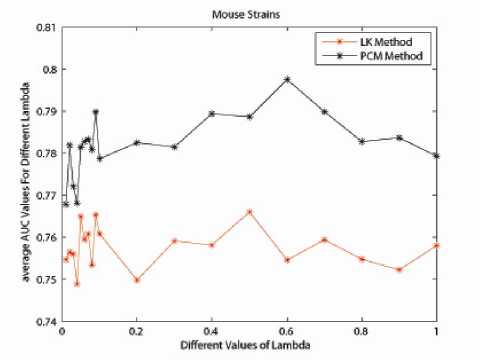
Figure 10.

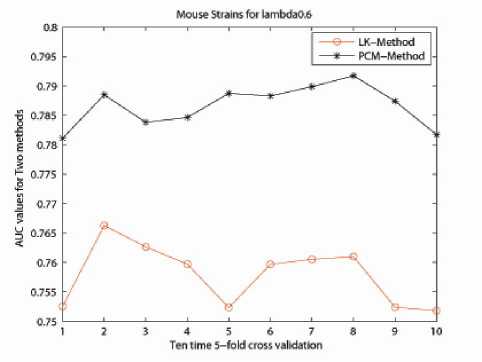
Figure 11.

We consider λ taking values from the set with uneven step size

For λ in [0.1,1], the step size is 0.1, while when λ in [0.01,0.1], step size 0.01 is adopted. For each value of λ, 10 times of 5-fold cross validation was performed on the two methods. The Y -label depicts the averaged AUC values of the corresponding methods. The curve with “*” indicates the 4-Spectrum Kernel method, the curve with “°” indicates our proposed PCM -Kernel method. Results elucidate that for all these λ, our proposed method has a much better performance. In fact, we see clearly that our developed method performs significantly better compared to 4-Spectrum Kernel method. This confirms the use of Eigen-matrix translation techniques.

• IV.    A D ISCUSSION ON E IGEN - MATRIX T RANSLATION T ECHNIQUE

It has been shown in the previous section that the Eigen-matrix translation technique is important for improving the classification accuracy. In order to show the strong generalization property of Eigen-matrix translation technique, we introduce another benchmark dataset for illustration. We tested on a data set related to Cystic fibrosis, containing 89 glycans related to cystic fibrosis, 107 related to respiratory mucin and 101 related to bronchial mucin. For cystic data sets, the total number of glycans is not the sum of each subclass because some glycans belong to several classes. Glycan structures in two of the data sets are retrieved from the KEGG/GLYCAN database [23] with annotations from CarbBank/CCSD database [24]. We then compared the classification accuracy results as performed by the LK-method and the PCM-method. The results by both methods are listed in Fig. 10. The well known Linkage Method (LK-method), is a weighted kernel method for classification of glycan data set. It was constructed based on the groundbreaking method: Q-gram Method [22]. And the classification accuracy of LK-method shows superiority to the Q-gram method. As can be seen clearly, for λ from [0.01,1], the algorithm by Eigen-matrix translation (PCM-method) performs much better compared to LK-method. When λ is chosen to be 0.6, the AUC value can achieve almost 0.8. Fig. 11 presents the classification performance of PCM-method compared to LK-method when λ is 0.6 for ten times. 5-fold cross validation was performed on both methods. Here x-label stands for the time performing 5-fold cross-validation and y-label is the AUC value for the classification. This further illustrates the robustness of Eigen-matrix translation in kernel construction.

From the excellent performance of our proposed PCM -Kernel Method, we can claim that the incorporation of physico-chemical information in similarity matrix construction and Motif Weight in kernel construction contributes a lot in improvement of classification accuracy. This would be of great help in understanding the mechanisms of glycan- binding proteins.

One more interesting phenomenon is that if we write the eigenvector matrix

X = [X1, X,K, X N У and

P = Diag {0,K0, A1,KAm} then the original kernel matrix before the procedure of Eigen-matrix Translation can be described as

m

T er PCM   /a '.N--m + iXN - m+i i=1

After making the Eigen-matrix Translation, the new kernel matrix can be expressed as rr m r r

KerPCM = N^v • v +L\XN-m+iXN-m+i i=1

where

r v =

N

NN

= 1                 i = 1

The newly included vector v exhibits a unique feature that the inner products of v with all the eigenvectors x_i , i = 1,..., N are the same. Since all the vectors are unit vectors, the vector v makes the same angle with all the existing vectors. The investigation of the special property of v will be of our further interest.

• V.    C ONCLUSION

In this paper, we have proposed a novel kernel in glycan-binding protein prediction problem which can be regarded as protein classification problem. Three innovations which mainly consider the involvement of background information enable higher accuracy in discriminating between classification groups. This confirms the necessity of including weighted motif information of specific protein which implies the necessity of constructing more biologically related tree kernels. Further applications of the proposed methods to other biological data sets and investigation of the Eigenmatrix translation techniques will be our future research issues.

A CKNOWLEDGMENT

The preliminary version of this paper has been accepted for presentation in ICBECS 2011 and publication in the proceedings of the 2nd International Conference on Biomedical Engineering and Computer Science (ICBECS 2011). Research supported in part by HKRGC Grant No. 7017/07P, HKU Strategy Research Theme fund on Computational Sciences, National Natural Science Foundation of China Grant No. 10971075 and Guangdong Provincial Natural Science Grant No. 9151063101000021.