Кинематическая генерация длинномасштабного магнитного поля течениями с зеркальной антисимметрией

DOI:

В настоящее время общепризнано, что источник магнитного поля многих астрофизических объектов (например, Солнца) — течение электропроводной жидкости [3]. Магнитогидродинамическая генерация описывается уравнениями Навье — Стокса и магнитной индукции (в совокупности, например, с уравнением теплопередачи), которые, в принципе, можно использовать для моделирования. Однако такой подход упирается в необходимость проводить вычисления с очень тонким пространственным разрешением, что требует чрезмерных вычислительных ресурсов. Желательно ограничить рассмотрение задачи на достаточно большие масштабы. Для этого теория электродинамики средних полей [2; 8] предлагает различные оценки воздействия малых масштабов, не участвующих в моделировании, на большие (аналогично замыканиям метода крупных вихрей в вычислительной гидродинамике [10]). Недостаток этого подхода состоит в необходимости принимать дополнительные гипотезы для вывода таких оценок. Однако при сильном разделении масштабов их вывод можно провести математически строго асимптотическими методами осреднения эллиптических операторов (см. [12] и ссылки в этой монографии). Это позволяет при изучении эволюции длинномасштабных линейных и слабо-нелинейных возмущений в теории магнитогидродинамической устойчивости независимо вычислять решения так называемых вспомогательных задач, описывающих короткомасштабные процессы и их воздействие на длинномасштабные процессы, и амплитудных уравнений, определяющих поведение длинномасштабных средних полей возмущений [5]. В данной работе мы следуем этому подходу к численному моделированию генерации магнитного поля стационарным течением несжимаемой электропроводной жидкости в рамках задачи о кинематическом динамо [3].

При рассмотрении кинематической генерации магнитного поля при наличии существенного разделения пространственных масштабов в рамках теории магнитогидродинамической устойчивости к длинномасштабным возмущениям сделан вывод (см., например, [12]), что два наиболее важных для генерации явления — α-эффект и вихревая диффузия — действуют на разных временны´ х масштабах. При наличии магнитного a-эффекта эволюция среднего магнитного поля h(X) подчиняется в главном порядке уравнению д h

= Vx х ( Ah )                            (1)

(отсутствие в нем диссипативных операторов второго порядка, отвечающих молекулярной или турбулентной диффузии — важное обстоятельство). Здесь T _s = e ^s t — так называемое медленное время; малый параметр задачи ε — отношение пространственных масштабов, описываемых быстрой пространственной переменной x порядка характерного размера структур генерирующего потока и медленной переменной X = e x ; t — быстрое время порядка периода оборота вихря в жидкости; A — тензор магнитного α-эффекта.

(Поля, зависящие только от быстрой пространственной переменной x, будем называть короткомасштабными, а зависящие также и от медленной переменной X = ex — длинномасштабными.) Если же α-эффект отсутствует (например, когда течение имеет центр симметрии), то эволюция среднего магнитного поля в главном порядке удовлетворяет уравнению дh                  Х3Х    Жк

97 2 = ⁿV x h + V X х gg D _mk— .              (2)

Здесь D _mk — тензор магнитной вихревой («турбулентной») диффузии.

Рассмотрим (следуя [5]) эволюцию средних магнитных полей, периодических по пространству, которые в начальный момент имеют вид длинномасштабных гармоник Фурье H e i q ^ X (где H — вектор-константа) и являются собственными функциями операторов α-эффекта или вихревой диффузии (задаваемых правыми частями уравнений (1) и (2) соответственно). Спектр оператора α-эффекта симметричен относительно мнимой оси [1], так как если гармонике H e i q ^ X отвечает собственное значение Л, то гармонике H e i ^{m q}X где _т — целое (при этом условии гармоника с растянутым в т раз волновым вектором удовлетворяет условию периодичности для первой), отвечает собственное значение тЛ. Таким образом, если действительная часть Л не равна 0, то новая гармоника H e i ^{m q} ^ X при соответствующем выборе знака т вырастает в e раз за время (e | m ReЛ | ) ¹ (в масштабе быстрого времени), а начальное поле, имеющее вид бесконечной суммы таких гармоник (то есть бесконечного ряда Фурье), будет расти сверхэкспоненциально. Оператор магнитной вихревой диффузии — второго порядка, поэтому если гармонике H e i q ^ X отвечает собственное значение Л, то гармонике H e ^{i m q} ^ ^X (где т — также произвольное целое число) отвечает собственное значение т ² Л. В отличие от случая оператора a-эффекта, растяжение в т раз волнового вектора q не меняет знак собственного значения; однако если собственное значение λ c положительной действительной частью существует (то есть имеет место явление отрицательной магнитной вихревой диффузии), то после такого растяжения новая гармоника вырастает в e раз за (быстрое) время (em' ² Re Л) ^{- 1} , а начальное поле, имеющее вид бесконечной суммы таких собственных функций (бесконечного ряда Фурье), растет сверхэкспоненциально, как и в случае оператора α-эффекта.

С математической точки зрения задача кинематического динамо — это часть задачи о линейной устойчивости немагнитного магнитогидродинамического состояния: поскольку магнитное поле воздействует на течение электропроводной жидкости посредством силы Лоренца, квадратичной по магнитному полю, задача о линейной устойчивости чисто гидродинамического состояния распадается на независимые подзадачи об устойчивости к гидродинамическим и магнитным возмущениям; вторая из них и есть задача кинематического динамо. Когда амплитуда начального возмущения достаточно вырастает, из-за действия силы Лоренца течение подвергается значительному возмущению, и оно, в частности, может утерять способность генерировать магнитное поле. Из приведенного выше анализа вытекает, что при действии α-эффекта самоуничтожение динамо вследствие неустойчивости может произойти на временах (в масштабе быстрого времени) порядка O(ε-1), а при его отсутствии и действии отрицательной вихревой диффузии — на временах порядка O(e-2). Таким образом, в рамках гипотезы о магнитогидродинамическом характере источника космических магнитных полей, по-видимому, астрофизическим приложениям в наибольшей степени отвечает такое устройство динамо, при котором все собственные значения оператора α-эффекта чисто мнимы, а рост магнитного поля на больших временах обеспечивает отрицательная магнитная вихревая диффузия.

Работа посвящена изучению генерации магнитного поля течениями с полем скорости, имеющим зеркальную антисимметрию относительно некоторой плоскости (в дальнейшем считаем, что это координатная плоскость х 1 = 0). Поле f = ( / 1 , / 2 , / 3 ) называют зеркально-симметричным относительно плоскости х 1 = 0 (или симметричным относительно декартовой координаты x 1 ), если при всех г выполнено

/г(-Х1,Х2,Хз) = (-1)51 /i(x), и зеркально-антисимметричным относительно этой плоскости (или антисимметричным относительно x1), если при всех г выполнено

/ i (-x i ,X 2 ,X 3 ) = ( - 1) ^{1 -5} 1 / i ( x );

здесь 5 * — символ Кронекера. Мы показываем, что течения из этого класса удовлетворяют сформулированному выше условию «максимально долгой работы динамо». Под действием α-эффекта в таких течениях среднее магнитное поле совершает гармонические колебания с конечным периодом в медленном времени Т 1 , и возникает анизотропная магнитная вихревая диффузия, способная при любой величине магнитной молекулярной диффузии п генерировать длинномасштабное поле в масштабе медленного времени Т ₂ . Астрофизические динамо функционируют при магнитных числах Прандтля Р _т из очень широкого интервала (см., например, [3; 6]), от весьма малых (например, в межзвездной среде) до весьма больших (например, геодинамо), при этом динамо при Р _т ^ 1 более сложны для анализа (см. [4]). Поскольку рассматриваемый здесь механизм генерации работоспособен при произвольной молекулярной диффузии, он может представлять определенную ценность для астрофизических приложений.

В теории электродинамики средних полей [2] показано, что если время корреляции турбулентного течения v мало (по сравнению с характерным временем диффузии магнитного поля), то след тензора α-эффекта пропорционален средней кинетической спиральности v • ( V х v ) (являющейся спиральностью завихренности V х v ). Вместе с тем известно [9], что способность гладкого (ламинарного) течения генерировать магнитное поле не связана с наличием у него ненулевой кинетической спиральности. Чтобы проиллюстрировать это, мы выбрали для численного исследования течение из так называемого семейства L (определенного в [9]), которое ортогонально завихренности в каждой точке пространства, то есть кинетическая спиральность которого поточечно равна 0.

по быстрым переменным ж ; кроме того, v ( x ) имеет нулевое среднее по ячейке периодичности T ³ быстрых переменных. Средняя по мелким масштабам и флуктуирующая части поля f ( x , X ) определяются равенствами

(f (x, X)) = уf(x, X) (2^ = £ (f)t e*,     {f} = f - (f), где e^ — орты декартовой системы координат.

В дальнейшем будем использовать следующие обозначения: дифференциальные операторы по медленным переменным маркируем нижним индексом X , а в операторе L , определенном равенством (4), предполагаем дифференцирование только по быстрым переменным.

Разложим решение уравнения (3) в степенные ряды по малому параметру задачи:

∞

h ( x , X ) = £ h n ( x , X )£ ⁿ ,                           (5.1)

n =0

∞

Л = £ Л п £ ^п .                                (5.2)

n =0

Подстановка этих рядов в (3) дает

∞

∑︁ n=0 \

L h n + n(2( V • V x ) h n - i

+ V X h n - 2 ) + ^V X

n\

X (v X hn-1)   £ ^ Лn-mhm 1 £ m=0/

Аналогично из условия соленоидальности магнитной моды находим, что для всех п >  0

выполнены равенства

Vx • ( h n ) = 0 ,

(7.1)

(7.2)

V- h n + Vx •{ h n - i } = 0 .

Приравняв к нулю коэффициенты ряда в левой части (6), получим иерархию уравнений, из которой с учетом (7.1) можно последовательно определить все коэффициенты разложений (5) [12].

• 1.1.    Уравнение порядка ε0

При п = 0 получаем из (6) первое уравнение в иерархии:

Lh0 = Л0h0, усреднением которого находим 0 = Л0 (h0). При малых £ собственное значение (5.2) мало отличается от λ0 , поэтому, если действительная часть λ0 не равна нулю, то при малых ε длинномасштабная мода (5.1) растет или затухает одновременно с короткомасштабной модой h0 , отвечающей собственному значению λ0 . Следовательно, при таком λ0 длинно-масштабность моды существенно не влияет на физический механизм работы изучаемого динамо. Случай чисто мнимого λ0 возможен, но не является случаем общего положения, и потому также не представляет особенного интереса. Соответственно, мы рассмотрим длинномасштабное динамо, для которого A0 = 0. Поскольку векторные поля-константы входят в ядро оператора, сопряженного к L, размерность ядра L не менее 3. Ограничимся рассмотрением случая общего положения, когда ядро короткомасштабного оператора L трехмерно.

При этих предположениях решение (8) имеет вид ho = £ (ho)k sk,                                 (9)

k=i где соленоидальные короткомасштабные нейтральные моды sk(x) — решения вспомогательных задач типа I:

L s k = 0 ,      (s k ) = e _k , V • s _k = 0

(доказательство их существования приведено в [12]).

• 1.2.    Уравнение порядка ε1

При n = 1 получаем из (6) следующее уравнение из иерархии:

Lh i + 2n( V • V x ) h o + Vx x ( v x h o ) = A i h o .                 (10)

Подстановкой (9) и усреднением находим условие его разрешимости (совпадающее с условием ортогональности в пространстве Лебега L 2 ( T 3 ) неоднородности ядру сопряженного оператора, то есть векторным полям-константам):

Vx x ( A ( h o ) ) = A i ( h o ) ,                              (11)

где тензор магнитного α-эффекта A состоит из столбцов

A k = ( v x S k ) .

Для поля скорости, антисимметричного относительно декартовой координаты ж 1 , он имеет следующую структуру:

	0	A 1 2	A 3 1 ⃦
A =	A 1 2	0	a 2 .                                 (12)
	A 3 1	- a 2	0

Следуя [7; 9; 12], рассмотрим пространственно-периодическое поле

( h o ) = H e i q ^ X .                                    (13.1)

Волновой вектор q удобно задать в сферических координатах с осью, направленной вдоль декартовой оси ж 1 :

q = (cos 0 , sin 0 cos ср , sin 0 sin ф) .                          (13.2)

Соленоидальность ( h g ) (см. (7.1) для п = 0) эквивалентна ортогональности постоянных векторов H и q . С учетом этой ортогональности, подставив (12) и (13) в (11), находим

Л ± = 1( а 2 ^ 1 ± ( A 3 ₉ 2 - А 2 ^ з )) ,                                      (14.1)

H + = ( - ( A 3 cos ф — A 2 sin ф) sin 0 , A 3 cos 0 , — A 2 cos 0) ,

H ^- = (0 , — sin ф , cos ф) .                                              (14.2)

Таким образом, собственные значения оператора α-эффекта для течения, антисимметричного относительно декартовой координаты, чисто мнимы.

После подстановки (13.1) флуктуирующая часть уравнения (10) теперь имеет вид

Lh i + e i qX |2in P H _k ( q • V ) s k + i q x |v x P H k S k| \ k =1                              k =1

—

λ 1

P H k { s k }) =0 . k =1        /

Отсюда hi = P I (hi)k Sk + eiq XHk I AiYk + i P Qmgmk   ,

k=i \                   \        m=i где Yk(x) и gmk (x) — короткомасштабные пространственно-периодические решения с нулевым средним вспомогательных задач типов II и II ′ :

Lg mk = — 2n — e m x { v x S k } ,     L Y k = { s k } .

^d^ m

• 1.3.    Уравнение порядка ε2

При п = 2 получаем из (6) уравнение

Lh 2 + 2n( V • V x ) h i + n V X h o + Vx x ( v x h i ) = A i h + A 2 h g .

Его усреднение после подстановки (9) и (15) дает

Vx x ( A ( h i ) )+ie ^{i qX} q x

P H k A i D k + iP Q m D mk k =i                m =i       /

= A i ( h i ) + (A 2 + r, - ^qX H , (16)

где тензоры вихревой диффузии состоят из столбцов

D k = ( v x Y k ) ,     D mk = ( v x g mk ) .

Для поля скорости, антисимметричного относительно декартовой координаты ж1, их структура такова:

D =	^  d2 D 2    0 D 3i — D	D ̃︀ 3 1 D ̃︀ 23 2    0	;                                                                     (18.1)
	0	D i,   D3A      D i   — D i, — D 14       D i   — D i, — D 14 12      11           21       22       23           31       32       33
D =	⃦ 1 ⃦ D 12	0     D 13       D 22    D 22    D 23       D 32    D 22    d 23		.
	⃦ 3 D 11	— D 2i3	0         D i23     D 223     D 323        D i33     D 233     D 333

(18.2)

В (18.2) каждая матрица размера 3 x 3 состоит из столбцов D _mk (17) при фиксированном т, возрастающем слева направо от 1 до 3.

Решение (16) имеет вид гармоники Фурье: (hi) = eiq^XH’. Постоянный вектор H’ ортогонален q в силу соленоидальности (7.1) для п = 1 и удовлетворяет уравнению iq x

£ Н Ai Dk + i£ qmDmk\ = k=i               m=i       /

- i q x ( AH ’ ) + A i H ’ + (A 2 + n) H .

Отсюда с учетом (12), (14) и (18) находим, что при A + = А - (случай общего положения)

A ± = Q i + Q i + ( Q i - Q i )cos2e ± Q 3 sin20 - n ,              (19.1)

где 1

Q i = - ^( D | A | + D 23 ) ,                                                         (19.2)

Q2 = 1 ((Di + Di + ADi - a3D3) cos 2y + (D^ - Di2 + A3Di + AD3) sin 2y+ 23       32       2   2       1   1                    33       22       1   2       21

+ D I3 - D 3i - A | D l - A 3 D 3 ) ,                                           (19.3)

гл  cosy , ।       ।   i   з _ ।  । з      sin ^y , з з   i   । i  i _

^Q 3 =  2   ^{( D} l3 ⁺ D 32   ^D i3  ^A i ^D 3   ^A 3 ^D i )    2   ^{( D} l3 ⁺ D 32 D il   ^A 3 ^D l  ^A2^D 3 ^{) +}

13      32      3   3     3     2     1   2     23

^{2 A} l D l3 + ² A i D 3i     ^A i ⁽² D 3i + D 23  D ll ) + ^A l ⁽² D l3 ^{+ D} 3l   D 33 ) ^{sin2 y}

• -I--ь----------------------------------------------------------------------------------------------------'

• 2. Численные результаты

4( A | sin y - A ³ cos y)

(19.4)

Соответственно, когда λ ₁ ^± мнимы (в том числе когда поле скорости антисимметрично по декартовой координате — см. (14.1)), λ ₂ ^± действительны.

В [9] рассмотрены шесть семейств течений несжимаемой жидкости с нулевой кинетической спиральностью. Течения так называемого семейства L имеют следующий вид:

v ( x ) = AV В - BVA.                        (20)

Если потенциалы Монжа A и В — скалярные собственные функции лапласиана, отвечающие одному и тому же собственному значению, поток (20) соленоидален. Для численного исследования выбран поток данного вида с 2п-периодическими по всем декартовым координатам потенциалами, отвечающими собственному значению - 18. Они состоят из гармоник Фурье с волновыми числами ( ± 3 , ± 3 , 0) и ( ± 4 , ± 1 , ± 1) и их перестановками (всего 36 волновых векторов). Когда A нечетно, а В четно по ж₁ , поток (20) антисимметричен по этой координате. Соответственно, выбранные потенциалы — линейные комбинации из 16 (в случае A ) или 20 (в случае В ) произведений тригонометрических функций

II {con} п.-. i=i с псевдослучайными коэффициентами, которые равномерно распределены на отрезке [— 1,1], где Л не содержит cos ть1 х1, а В — sin п1 х1. Поле нормализовано так, что его среднеквадратичная величина равна 1. Рисунки изоповерхностей плотностей кинетической энергии 2|v|2 (рис. 1а) и завихренности V х v (рис. 1б) рассматриваемого течения показывают, что оно имеет достаточно нетривиальную структуру, что, по-видимому, положительно сказывается на способности этого течения генерировать магнитное поле.

Будучи доминирующими (то есть имеющими максимальный инкремент роста), короткомасштабные нейтральные магнитные моды s^ (x) вычислены кодом [11] с применением псевдоспектральных методов. График коэффициента магнитной вихревой диффузии neddy (ф) = — max Л±

(рис. 2) иллюстрирует сингулярное поведение инкрементов роста магнитного поля λ ₂ ^± (19) как функции азимутального направления ϕ в некоторой малой окрестности критического азимутального направления волнового вектора q , при котором знаменатель дроби, входящей в выражение (19.4) для Q 3 , становится равен нулю. Такое сингулярное поведение имеет место при любом коэффициенте магнитной молекулярной диффузии η. При этом, в любой малой окрестности критического азимутального направления знаменатель дроби, входящей в (19.4), принимает как положительные, так и отрицательные значения. Соответственно, в некоторой малой окрестности критического азимутального направления один из инкрементов λ ₂ ^± положителен, каково бы ни было η. Отметим также жесткую фокусировку рассматриваемого динамо: вне некоторого малого интервала ϕ вокруг критического направления инкремент роста (убывания) магнитного поля λ ₂ ^± (19) очень слабо зависит от азимутального направления, то есть генерируемое магнитное поле имеет вид волны, распространяющейся в пространстве вдоль четко выраженного конуса направлений.

а

б

Рис. 1. Изоповерхности плотности кинетической энергии поля скорости течения (а) и его завихренности (б) на уровнях 15 % и 25 % максимумов соответственно

Выводы

Нами описано двумасштабное динамо, работа которого основана на совместном функционировании двух важнейших механизмов генерации длинномасштабного магнитного поля: α-эффекта и анизотропной отрицательной вихревой диффузии, ответственных за гармонические колебания магнитного поля и его рост соответственно.

Это динамо работает при любых коэффициентах магнитной молекулярной диффузии, когда разделение масштабов настолько велико, что первые члены асимптотических разложений (5) достаточно точно описывают эволюцию доминирующей магнитной моды.

Обращение в ноль кинетической спиральности течения не препятствует функционированию ни магнитного α-эффекта, ни вихревой диффузии. Представляется, что никакие функционалы вида спиральности некоторого поля не могут описать способность гладкого течения генерировать магнитное поле.

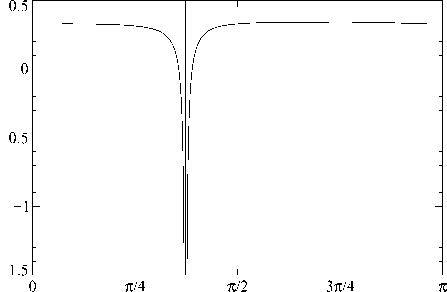
Рис. 2. Зависимость коэффициента вихревой диффузии η eddy (вертикальная ось) от азимутального направления ϕ (горизонтальная ось) волнового вектора (13.2) при п = 0, 3

ПРИМЕЧАНИЕ

• ¹    Р.А. Чертовских был поддержан проектом POCI-01-0145-FEDER-006933/SYSTEC, финансируемым ERDF (European Regional Development Fund) в рамках программы COMPETE 2020 (Programa Operacional Competitividade e Internacionalizac¸a˜o) и фондом FCT (Fundac¸a˜o para a Cieˆncia e a Tecnologia, Португалия). Основной объем вычислений выполнен на кластере «Сергей Королев» Самарского университета.