Кинематическая параметризация кривошипно-ползунной группы Альфа-Стирлинга

В настоящее время интерес к двигателям внешнего сгорания вновь возрастает. Причин тому несколько. Во-первых, качественное углеводородное топливо не является неистощимым ресурсом на планете. Во-вторых, цена традиционных энергоносителей постоянно растёт, в том числе и из-за истощения доступных запасов. В-третьих, при этом всё с большей актуальностью встаёт вопрос получения электроэнергии.

Особенно этот вопрос актуален для удалённых районов с малоразвитой инфраструктурой, различных экспедиций и исследовательских станций. Сейчас вопрос их энергоснабжения, как правило, решается за счёт дизель-генераторов. Такое решение весьма дорого, как само по себе (1 кВт^час сжигается 0,2 л дизельного топлива [ 1 ]), так и его логистическое обеспечение — зачастую очень накладно доставлять топливо в требуемые районы.

При этом в этих отдалённых районах бывает достаточно много других типов энергоресурсов, как правило, твёрдых. Это могут быть уголь, дрова, торф и т. д. Данные виды энергоресурсов отлично подойдут в качестве источника энергии для двигателя, работающего по принципу Стирлинга.

Хотя двигатели Стирлинга известны достаточно давно [ 2] , их разработка и совершенствование строились на базовых основах термодинамики и огромном объёме экспериментальных исследований [ 3 ]. Поэтому данные двигатели не смогли выдержать темпы развития обладающих отлично разработанной теоретической базой двигателей внутреннего сгорания.

Теоретическое рассмотрение процессов, протекающих в двигателях Стирлинга, ограничено исследованием отдельных элементов и закономерностей, таких как шаттл-эффект в системе «вытеснительный поршень-цилиндр» [ 4] , тепловые потоки системы «рабочее тело — регенератор» при изменении направления движения газа, влияние «мёртвого объёма» на КПД и удельную мощность [ 5 ] и т. д.

Комплексное же рассмотрение рабочего процесса двигателя Стирлинга и разработка общей теории остаётся нерешённой задачей. Такая задача практически неразрешима аналитическими методами. Для её решения необходимо применять численные методы решения связанных задач [ 6 ]. Под связанными задачами понимаются задачи гидрогазодинамики (в т. ч. с фазовыми переходами), теплопередачи, механики деформируемого тела в одной численной модели исследуемого механизма, в так называемой «явной постановке», т. е. позволяющей исследовать быстротекущие процессы [ 7 ].

При правильном подходе будет возможно получить оптимальные конструктивные и технологические параметры двигателя Стирлинга и получить максимально эффективную энергетическую машину, реализующую цикл Стирлинга без решения таких фундаментальных задач, как, например, герметизация рабочего тела [ 8 ].

2.    Материалы и методы

Задачей теоретического исследования данной статьи является определение кинематической зависимости положения поршней двигателя Стирлинга типа «Альфа» [ 9] . Данные зависимости позволят разработать численную протомодель двигателя и исследовать динамику перетекания газов из горячей полости в холодную.

Кинематическая схема двигателя представлена на рисунке.

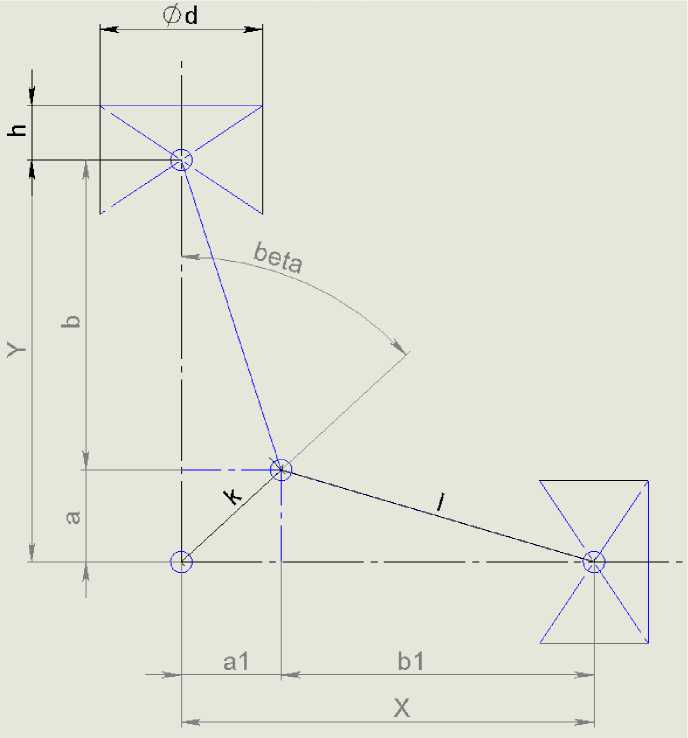
Рисунок. Кинематическая схема двигателя Стирлинга типа «Альфа»

Постановка задачи следующая: перемещение вертикального поршня ( Y) будет задано гармонической функцией. Так как на данном этапе исследуется исключительно газодинамическая задача, то в моделировании механической части нет необходимости. Это позволит существенно сократить ресурсоёмкость выполнения моделирования. Инерционную составляющую кривошипно-ползунного механизма учтём моментом инерции маховика J_M. Далее, необходимо вывести зависимость положения горизонтального поршня от положения вертикального X(Y), что позволит в дальнейшем исследовать взаимное изменение объёмов горячей и холодной полостей и динамику перетекания газа.

3.    Результаты

Как видно из рисунка, угол между осями поршней составляет 90°. Данный параметр многими исследователями считается оптимальным для получения максимальной удельной мощности. На данном этапе мы примем данную гипотезу, но в дальнейшем подвергнем её проверке в процессе численного моделирования. Система уравнений координат перемещений вертикального и горизонтального поршней в зависимости от угла поворота коленчатого вала будет иметь следующий вид:

Y = k • cos

X = k • sin

в + V 1 2 - ( k • sin в ) 2 в + V l ² - ( k • cos в ) 2

Далее, необходимо определить вид уравнения (1). Для этого определим координату горизонтального поршня X в следующем виде:

X = ai + b(2)

или (см. рисунок)

X = 4k2 - a2 + 4l2 - a2 .(3)

При этом параметр а будет равен:

a = Y - b .(4)

Таким образом, подставляя (4) в зависимость (3), получаем:

X = Vk2 - (Y - b)2 + Vl2 - (Y - b)2 .(5)

Далее, рассмотрим параметр b . Данный параметр может быть определён как через разность X – a , так и через треугольник Δ(la 1 b) (см. рисунок). Сведём данные зависимости в систему:

b = Y - a

^b = ^l ² - ^a 2

Как видно из системы, в ней присутствуют параметры а и а 1 . Учитывая жёсткость треугольника Δ(Ylk) , т. к. l и k являются константами, отношение параметров а и а 1 будет отражать угол положения коленчатого вала β. Тогда

a 1 = k - a .

Подставляя эту зависимость во второе уравнение системы (6), получим следующее:

b = л]l2 - (k2 - a2) = Vl2 + k2 + a2 .(8)

Учитывая уравнение (7), получаем:

b = a)l2 + k2 + (Y - b)2 = Vl2 + k2 + Y2 - 2Yb + b2 .(9)

Возведём полученное уравнение в квадрат:

b2 = l2 + k2 + Y2 - 2 Yb + b2.(10)

Выразим b :

b ² + 2Yb - b ² = l ² + k ² + Y ²

2Yb = l2 + k2 + Y2.

, l ² + k ² + Y ² b =----------

2 Y

Подставим полученное выражение в уравнение (5):

X =

k ² - ( У

-

l ⁺ k ^{+ У} )² +_л l² - ( У 2 Y

-

l ² + k ² + У ² ₂

2 Y ^{) .}

Рассмотрим вычитаемое подкоренной разности. Упростим его:

l ² + k ² + У ²

2 Y

у - (

l ² + k ²

2 Y

2    22

+_) = у - L+k_ 2 Y        2 Y

-

Y

у - 1 ² + k ² 2 2 У

Окончательно имеем вид уравнения, описывающего взаимосвязь координаты горизонтального поршня относительно координаты вертикального:

x(у) = k2 - (_ -l-+L)2 + l2 - (_ -L+k-)2.(14)

2    2Y            22

4.    Обсуждение и заключение

Полученное уравнение позволит достаточно просто смоделировать цикличное перетекание газа из горячей полости в холодную. Далее, увеличивая частоту вращения коленчатого вала, можно будет исследовать возрастание аэродинамического сопротивления газа в рабочем объёме. Отсутствие в итоговом уравнении угла поворота коленчатого вала позволит упростить численную модель системы и снизить ресурсоёмкость выполнения расчёта.

В данном моделировании приняты определённые упрощения, например, одинаковые длины шатунов l (см. рисунок). В дальнейшем система будет приведена к общему виду, который позволит учитывать и изменять большинство параметров.