Кинематические и динамические характеристики установившегося нестационарного движения элитных пловцов

Биомеханические исследования водных локомоций человека показывают, что наиболее сложным и принципиальным является изучение причин возникновения на поверхности тела человека движущей силы и силы гидродинамического сопротивления. Поэтому, в отличие от технических объектов, у человека при плавании отсутствует четкое разделение гидродинамических функций на пассивный корпус, который испытывает только сопротивление движению, и активный движитель, создающий силу тяги.

Необходимость дополнения существующей эффективной технологии кинематического анализа плавания человека экспериментальными динамическими характеристиками специалисты понимали достаточно давно. Наибольшее распространение и признание получил метод, разработанный R. Schleihauf [15]. Предложенный им трехмерный биомеханический анализ техники плавания является одним из наиболее эффективных методов определения кинематических характеристик системы движений пловца непосредственно в условиях соревновательной деятельности. В то же время квазистационарный расчет тотальной и эффективной пропульсивных сил изолированной кисти руки по известным для нее стационарным значениям гидродинамических коэффициентов подъемной силы и лобовой силы является методом приближенной оценки нестационарных режимов взаимодействия реального движителя с гидродинамическим потоком.

Кроме того, в этом случае не принимаются во внимание характерные для нестационарного движения значительные инерционные силы и внутрицикловой сдвиг продвигающих сил и сил гидродинамического сопротивления по фазе. Поэтому до сих пор не удавалось определить количественно реальные внутрицикловые продвигающие силы и силы гидродинамического сопротивления, возникающие на уровне целостной биомеханической системы водных локомоций человека и сопоставить эти динамические характеристики с ключевыми кинематическими, т.е. внутрицикловыми показателями скорости и ускорения.

В то же время закономерности равномерного и нестационарного движения человека в водной среде существенно отличаются [9, 14]. На сегодняшний день отсутствуют надежные сведения о реальных биомеханических механизмах и закономерных зависимостях установившегося нестационарного плавания человека, что сдерживает дальнейший прогресс в подготовке элитных пловцов.

В процессе специального исследования решались следующие задачи:

• 1.    Разработка экспериментального метода для определения основных биомеханических характеристик нестационарного плавания человека различными стилями.

• 2.    Изучение закономерностей установившегося нестационарного движения элитных пловцов в водной среде.

Метод исследования

Математическая модель биогидродинамического метода

Взаимодействие двух горизонтальных сил, как правило, не равных по мгновенным значениям и противоположно направленных, продвигающей силы и силы гидродинамического сопротивления в цикле плавательных движений, описывается уравнением установившегося нестационарного поступательного движения тела пловца в жидкости [10]

• ^Fp ( e .) ⁽ t ) - ^Fr ( f . d .) ⁽ t ) = ⁽ m 0 + ^A m ) ^{X d}ul^{dt                            (1} )

где F p ( e .) ( t ) – мгновенное значение эффективной продвигающей силы, генерируемой пловцом (т.е. суммарной силы, создаваемой движителями пловца и возникающей в результате рабочих движений рук, ног и, в некоторых стилях плавания, туловища); F r ( f.d. ) ( t ) – мгновенное значение лобовой компоненты силы активного (полного) гидродинамического сопротивления тела пловца при нестационарном движении; m о - масса тела пловца; A m - присоединенная масса жидкости инерционного происхождения; du ( c.m. ) / dt – производная скорости по времени, т.е. мгновенное ускорение центра масс тела человека.

Величина присоединенной массы жидкости инерционного происхождения определяется на основании выражения

A m = m ₀ x k 11 ,                                     (2)

где k 11 – безразмерный коэффициент присоединенной массы жидкости.

Наиболее сложным вопросом в используемом подходе является определение мгновенных значений F r ( f.d. ) ( t ). Это делается на основании уравнения гидродинамической реакции

F rvd) ( t ) = C x(n) ( t ) X (Р/2) X S (bs) ( t ) x u \,_H ( t ),                         (3)

где C x ( n. ) ( t ) – мгновенное значение безразмерного коэффициента лобовой силы гидродинамического сопротивления, соответствующее нестационарному режиму движения тела; p - плотность воды {кым^-3}; S ( b.s. ) ( t ) - мгновенное значение характерного гидродинамического размера тела испытуемого {м²};

u ( p.b. ) ( t ) – мгновенное значение скорости точки на поверхности тела человека при плавании {м∙с^–1}.

В свою очередь, C x ( n. ) ( t ) представляется выражением

C x ( n) ( t ) = C x ( fd) ( t ) + A C x ( n.) ( t ) (Re 1 , Fr, a ),                             (4)

где C x ( f.d. ) ( t ) – мгновенное значение безразмерного коэффициента лобовой силы гидродинамического сопротивления, соответствующее стационарному режиму движения тела; A C x ( n ) ( t ) - мгновенное значение безразмерного коэффициента дополнительного вязкостного гидродинамического сопротивления, обусловленного нестационарностью движения; Re l – число Рейнольдса; Fr – число Фруда; a – безразмерное ускорение

Взаимодействие плывущего человека с водной средой имеет механическую природу, поэтому корректный теоретический анализ в сочетании с натурными опытами и биогидродинамическими испытаниями возможен только с позиций теории механического подобия и размерностей нестационарных процессов [1, 6]

Нестационарность плавания человека характеризуется прежде всего неравномерным поступательным движением со скоростью центра масс тела ( c.m. ) с переменной по времени ( t ) мгновенной скоростью ( u ), так что u = u ( t )

Важнейшей характеристикой является средняя скорость плавания ( u 0 ) в данном режиме на участке пути определенной длины ( l ):

1t

Uo = “ u(t) dt = - t0

Соответственно, безразмерная средняя скорость плавания определяется одним из критериев теории механического подобия – безразмерным числом Фруда (Fr) (относительная скорость), которое характеризует отношение сил инерции к силам тяжести

Fr = u 0/ 4g ^x L •                                  (6)

Здесь g – гравитационное ускорение {м/с2}, L – длина тела испытуемого {м} Критерий подобия Fr необходимо учитывать при движении тел с интенсивным волнообразованием на свободной поверхности, что и имеет место при плавании человека

При изучении нестационарного плавания биологических объектов используются еще два определяющих гидродинамических безразмерных числа – критерии Рейнольдса (Re l ) и Струхаля (Sh u ) Они выводятся из дифференциальных уравнений движения вязкой несжимаемой жидкости (уравнения Навье-Стокса), физически представляют собой отношения соответствующих сил, рассчитанных на единицу массы жидкости, и определяются через характерные параметры движения, присущие плаванию изучаемого биологического объекта (в данном случае – человека)

Критерий Рейнольдса представляет собой отношение конвективных (переносных) сил инерции и сил вязкости (внутреннего трения) жидкости и определяется выражением

Re l = u ₀ x LV • (7)

Здесь u 0 , L обозначены так же, как ранее; ν – кинематический коэффициент вязкости воды, зависящий от ее температуры Значение ν при средней температуре воды в плавательных бассейнах 27^oС равно 0,90∙10^–6 м²/c

Степень неравномерности плавания в различные моменты цикла движений наиболее точно оценивается абсолютным ускорением центра масс тела человека a ( c.m. ) = du ( t )/ dt и его безразмерной величиной

L    du ( t )

a = —_ —x--- u ² ( t )     dt

Однако для использования выражения (8) требуется бóльшая информация о кинематике нестационарного плавания, что не во всех случаях, имеющих место при анализе в данной работе, достижимо. Поэтому используется критерий Струхаля (Sh u ), характеризующий неравномерность всего (полного) цикла движений пловца различными спортивными стилями. Критерий представляет собой отношение локальных (местных) и конвективных сил инерции жидкости и определяется выражением

S = I_ _x ^{2 du}_ .                                  (9)

u 2 ^u 0 ^T

Здесь, применительно к плаванию человека, 2 du – удвоенная разница между максимальной скоростью ( u max (c.m.) ) и минимальной скоростью ( u min (c.m.) ) центра масс тела человека в цикле движений стилями плавания дельфин и брасс, T – время одного цикла регулярно повторяющегося процесса (период) {с}. Для стилей плавания вольный стиль и кроль на спине 2 du полного цикла равно 2 du полуцикла движений правой рукой плюс 2 du полуцикла движений левой рукой.

Критерии Fr, Re l и Sh u полностью определяют динамическое подобие нестационарного плавания человека с интенсивным волнообразованием и позволяют использовать с минимальными и контролируемыми допущениями необходимые экспериментальные данные, полученные в гидробионике, биомеханике, гидромеханике, а также сопоставлять результаты, полученные на "модели" и "натуре" в ходе выполнения данного экспериментального исследования.

В данном исследовании диапазон значений числа Fr заключен между минимальной величиной в 0,32 (брасс, женщины) и максимальной величиной в 0,46 (кроль на груди, мужчины).

Диапазон значений числа Re l заключен между минимальной величиной в 2,58∙10⁶ (брасс, женщины) и максимальной величиной в 4,46∙10⁶ (кроль на груди, мужчины). Указанный диапазон числа Re l входит в область сравнительно высоких чисел Re l = 10³–10⁷ с преобладающим значением сил инерции [1, 5].

В указанном выше диапазоне чисел Re l и Fr при стационарном режиме движения тела спортсмена вязкостное сопротивление составляет 85–90% от полного гидродинамического сопротивления [3].

Диапазон значений числа Струхаля Sh u заключен между минимальной величиной в 0,137 (кроль, мужчины) и максимальной величиной в 1,410 (брасс, женщины).

Технология определения переменных математической модели

Для решения уравнения (1) с целью определения искомой величины мгновенного значения эффективной пропульсивной силы ( F p ( e. ) ( t )) мы должны иметь экспериментальные значения du (_c._m.) / dt , F rfd. ) ( t ) и A m .

Скорость и ускорение центра масс тела

Акустическим способом (с использованием эффекта Доплера) первоначально измеряются значения мгновенной поступательной скорости точки на поверхности тела человека при плавании с предельной скоростью ( u ( p.b. ) ( t )) [2]. Одновременно проводится подводная и надводная видеозапись движений испытуемого [16]. Все видеокамеры фокусируются на средней части плавательной дорожки на отметке 40 метров от старта, на которой проводится тестирование. Для анализа кинематических и динамических характеристик плавания испытуемого выбирается один цикл движений в районе указанной отметки.

Далее, с использованием пакета специальных прикладных программ, на основании синхронизированной видеозаписи плавания испытуемого проводится трехмерный кинематический анализ движения всех основных звеньев тела человека. На основании результатов этого анализа, с использованием методики D. Troup [12, 15], учитывающей массы и моменты инерции основных звеньев тела, экспериментальные значения u ( p.b. ) ( t ) трансформируются в значения мгновенной поступательной скорости центра масс тела испытуемого ( u ( c.m. ) ( t )). Значения мгновенного ускорения центра масс тела человека ( a ( c.m. ) ( t )) определяются по временным производным ( du ( c.m. ) / dt ).

Лобовая компонента силы активного гидродинамического сопротивления тела пловца при нестационарном движении

Лобовая компонента силы F r ( f.d. ) ( t ) определяется на основании экспериментального определения переменных уравнения (3).

Мгновенное значение характерного размера тела испытуемого ( S ( b.s. ) ( t )) определяется как конкретная величина объема тела испытуемого, находящаяся в воде в данный момент времени, в степени 2/3 {м²}. В указанный объем не включаются объемы звеньев тела, которые в данный момент цикла являются движителями и имеют отрицательный вектор по отношению к направлению поступательного движения центра масс тела испытуемого. Данная величина определяется экспериментально на основании результатов трехмерного кинематического анализа движения всех основных звеньев тела человека.

Мгновенные значения C x ( f.d. ) ( t ) для каждого испытуемого определяются в различном количестве наиболее характерных положений тела испытуемого (от 6 до 12 исследуемых позиций в зависимости от стиля плавания). Данные позиции также отбираются на основании предварительного кинематического анализа видеозаписи.

В зависимости от исследуемой позиции тела испытуемого C x ( f.d. ) ( t ) определяется при стационарном режиме обтекания двумя различными путями. В первом случае, когда S ( b.s. ) ( t ) исследуемой позиции не имеет каких-нибудь исключаемых сегментов движителей, C x ( f.d. ) ( t ) рассчитывается на основании измерения результатов гидродинамического сопротивления испытуемого в гидроканале.

Во втором случае, когда S ( b.s. ) ( t ) исследуемой позиции имеет исключаемые сегменты движителей, используются экспериментальные значения C x ( f.d. ) ( t ) специальной модели человеческого тела [11, 13]. Так, например, в стиле дельфин в фазе оттакивания исключаются определенные сегменты рук или в стиле брасс в фазе удара ногами исключаются определенные сегменты ног. Модель человеческого тела длиной 1,85 метра исследовалась в гидроканале при стационарном режиме обтекания в диапазоне чисел Re l = (1,0–5,0)∙10⁶ при скоростях гидродинамического потока до 2,2 м/с. Конструкция модели позволяет исключать любые объемы сегментов человеческого тела, которые в данный момент являются движителями, и, следовательно, не испытывают фронтального гидродинамического сопротивления. Такой подход позволил определить экспериментальные зависимости между C x ( f.d. ) ( t ) и различным объемом исключаемых сегментов движителей модели во всех изучаемых стилях плавания. Модель исследовалась во всех рассматриваемых позициях тела испытуемого с различными значениями S ( b.s. ) ( t ).

Для определения ∆ C x ( n. ) ( t ) использовались экспериментальные значения коэффициента дополнительного вязкостного сопротивления при нестационарном движении твердого тела вращения (рис. 1), которые были получены в процессе специального экспериментально-теоретического исследования [8]. Были проведены специальные испытания данного тела длиной L = 1,5 м, наибольшим диаметром d = 0,21 м (удлинение L/d = 7,15), при движении тела вблизи свободной поверхности.

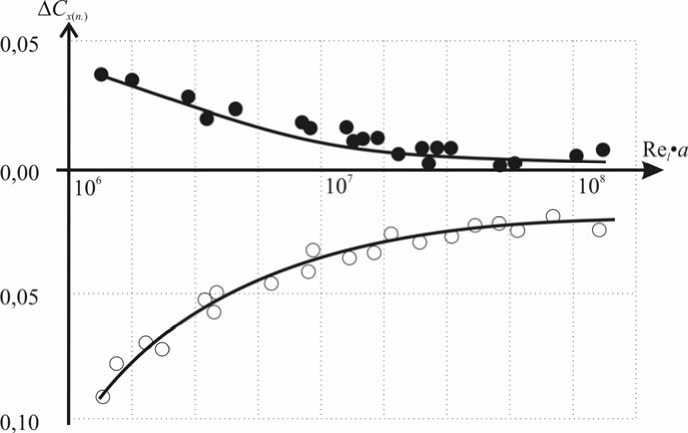
Рис. 1. Экспериментальные значения безразмерного коэффициента дополнительного вязкостного сопротивления при нестационарном движении твердого тела вращения согласно линейному закону изменения скорости ∆ C x ( n. ) (Re l ∙ а ^-1): • – положительное ускорение, ○ – отрицательное ускорение.

Нестационарные испытания проводились при скоростях буксировки тела до 3,0 м/с, в диапазоне чисел Re l = (1,0–5,0)∙10⁶ согласно трем законам изменения скорости: по линейному с положительным и отрицательным ускорением, по экспоненциальному, по синусоидальному. Диапазон критериев подобия Fr, Re l и безразмерного ускорения ( a ), используемый при этом исследовании, полностью включает диапазон этих показателей для испытуемых данного исследовательского проекта, что и является объективным основанием для использования полученных экспериментальных значений ∆ C x ( n. ) ( t ). Анализ результатов, представленных на рис. 1, отчетливо показывает, что положительное ускорение приводит к увеличению вязкостного сопротивления тела, а отрицательное ускорение уменьшает его значения.

Мгновенные значения C x ( f.d. ) ( t ), ∆ C x ( n. ) ( t ) и S ( b.s. ) ( t ) вводились в прикладную компьютерную программу для расчета F r ( f.d. ) ( t ) с дискретностью, зависящей от числа наиболее типичных позиций тела испытуемого в анализируемом цикле движений.

Присоединенная масса жидкости инерционного происхождения (Am)

Величина ∆ m определялась на основании уравнения (2). Значения безразмерного коэффициента ( k 11 ) определялись экспериментально (на основании натурных испытаний), т.е. путем сравнения результатов измерения пассивного гидродинамического сопротивления ( F r ( p.d. ) ) на устаноновке гравитационного типа ( du / dt = 0) и инерционным методом ( du / dt ≠ 0) [11, 13]. Диапазон значений k 11 для испытуемых данного проекта заключен между минимальной величиной в 0,097 и максимальной величиной в 0,139. Эти значения k 11 близки к значению коэффициента присоединенной массы для равновеликого эллипсоида вращения в поступательном нестационарном движении вдоль длинной оси ( k 11 = 0,09), которое обычно используют при исследовании гидробионтов, где возможность экспериментального определения k 11 отсутствует [5].

Полезная внешняя механическая мощность (Puo), тотальная внешняя механическая мощность (Pto) и пропульсивная эффективность (ep)

Установившееся нестационарное движение предполагает сохранение постоянной средней скорости плавания биологического объекта в течение нескольких последовательных биомеханических циклов (u0(c.m.) = const). Основным условием такого движения, очевидным из уравнения (1), является равенство средних значений Fp(e.) и Fr(f.d.) за анализируемый цикл (Fp(e.) – Fr(f.d.) = 0). В свою очередь, также очевидным и неоднократно экспериментально подтвержденным является равенство в данном цикле и средних значений тотальной продвигающей силы (Fp(t.)) и силы активного гидродинамического сопротивления (Fr(a.d.)) [10, 12, 13, 18].

Полная величина F p ( t. ) представляется суммой трех составляющих

F p ( t.) = F p ( e .) + F + F 2 ,                                   (10)

где F p ( e. ) – эффективная пропульсивная сила, идущая на преодоление F r ( f.d. ) ; F 1 – сила, расходуемая на перемещение специфической массы воды назад, необходимое для создания пропульсивной силы; F 2 – сила, расходуемая на образование турбулентных вихрей при взаимодействии движителя с водной средой и на индуктивное сопротивление движителя Отсюда становиться очевидной и физическая разница между F r ( a.d. ) и F r ( f.d. ) , которые одновременно должны определяться разными экспериментальными методами, специально ориентированными на измерение соответствующих сил в условиях нестационарного движения испытуемого Поэтому одновременно с измерением акустическим способом значений u ( p.b. ) ( t ), методом малых возмущений определяется величина F r ( a.d. ) [9] и на основании стандартного уравнения гидродинамической реакции рассчитывается безразмерный коэффициент силы активного гидродинамического сопротивления ( C x ( a.d. ) )

Безразмерный коэффициент эффективности ( C e ) определялся как отношение среднего значения F p ( e. ) к среднему значению F p ( t. ) движителей испытуемого в цикле Индивидуальное значение C e вводилось в программу в качестве постоянной величины для определения мгновенных значений F p ( t. ) ( t ) в анализируемом цикле движений

Fp (t.)(t) = Fp (e)( t)/Ce.(11)

Полезная внешняя механическая мощность ( P uo ) и тотальная внешняя механическая мощность ( P to ) определялись соответственно по следующим формулам:

Puo = Fr(f.d.) X u0(c.m.),

Pto = Fr(a.d.) X u0(c.m.), где u0(c.m.) – средняя скорость центра масс тела испытуемого в анализируемом цикле.

Пропульсивная эффективность ( e p ) определялась следующим образом [5, 10, 16]:

ep = Puo f Pto ■(14)

При графическом представлении индивидуальных результатов биомеханического анализа цикла плавательных движений человека, мгновенные значения показателей поступательной скорости ( u ( c.m. ) ( t )) и ускорения центра масс тела ( a (c.m.) ( t )), лобовой компоненты силы активного гидродинамического сопротивления тела ( F r(f.d.) ( t )), суммарной эффективной ( F p ( e. ) ( t )) и суммарной тотальной ( F p(t.) ( t )) продвигающих сил движителей апроксимировались полиномами соответствующих степеней и выводились на экран дисплея или принтер.

В данной работе для описания и обозначения фаз движений в цикле используется классификация этого процесса, предложенная Р.Б. Хальяндом [7]. Каждый график содержит индивидуальные временные характеристики всех фаз движений в полном цикле и сопровождается графическим изображением граничных моментов этих фаз.

Организация исследования

Экспериментальное исследование было осуществлено в периоды непосредственной подготовки испытуемых к летним Олимпийским играм 1992 года в Барселоне и 1996 года в Атланте, а также к чемпионату мира по плаванию 1994 года в Риме. В исследовании приняли участие две испытуемых женского пола и семь испытуемых мужского пола в возрасте от 17 до 26 лет. Все испытуемые на момент тестирования входили в первую десятку спортсменов мирового рейтинга.

Биогидродинамический анализ системы движений проводился предельно близко к дате главного старта сезона, когда испытуемый начинает входить в так называемое состояние "спортивной формы" и достигает максимальных показателей скорости плавания.

Результаты и их обсуждение

На рис. 2–10 представлены результаты индивидуального биогидродинамического анализа плавания испытуемых различными спортивными стилями. Кроме того, средние значения основных экспериментальных показателей за анализируемый цикл движений испытуемого, а также другие индивидуальные характеристики, необходимые для экспериментального решения поставленных задач, представлены в таблице. На рис. 11 и 12 представлены итоговые критериальные зависимости между числами Струхаля (Sh u ) и Рейнольдса (Re l ), а также числом Струхаля (Sh u ) и безразмерным коэффициентом гидродинамической силы ( C x ( a.d. ) ), полученные экспериментально в ходе реализации проекта.

Анализ индивидуальных результатов показывает, что использование биогидродинамического метода позволило впервые определить количественно реальные внутрицикловые продвигающие силы и силу лобового гидродинамического сопротивления, возникающие при плавании различными стилями на уровне целостной биомеханической системы водных локомоций человека.

Сопоставление полученных динамических характеристик с кинематическими показало, что внутрицикловые изменения мгновенных значений поступательной скорости центра масс тела человека ( u ( c.m. ) ( t )) во всех спортивных стилях плавания жестко взаимосвязаны с определенными фазами циклов. Кроме того, эти изменения четко количественно детерминированы разницей мгновенных значений эффективной продвигающей силы ( F p ( e. ) ( t )) и силы лобового гидродинамического сопротивления ( F r ( f.d. ) ( t )). Независимо от стиля плавания основными причинами максимальных значений тотальной и эффективной продвигающих сил в определенных фазах цикла являются оптимальные скорости движителя и значительное увеличение мгновенных значений характерного размера движителя за счет эффективной гидродинамический ориентации. Только в стилях плавания дельфин и брасс в определенных фазах цикла возникают отрицательные значения эффективной продвигающей силы, связанные с подготовительными движениями рук и ног.

Во всех изучаемых стилях плавания наблюдается фазовый угол сдвига (Δθ) между пиковыми значениями эффективной продвигающей силы ( F p ( e. ) ( t )) и силы лобового гидродинамического сопротивления ( F r ( f.d. ) ( t )). Среднее значение Δθ у испытуемых данного проекта составляет величину, близкую к 0,5 π радиан (диапазон колебаний от 0,27 π радиан до 0,67 π радиан). Экспериментальные исследования плавания гидробионтов показали, что фазовый угол сдвига, равный 0,5 π радиан, соответствует максимальным значениям пропульсивной эффективности последних [17].

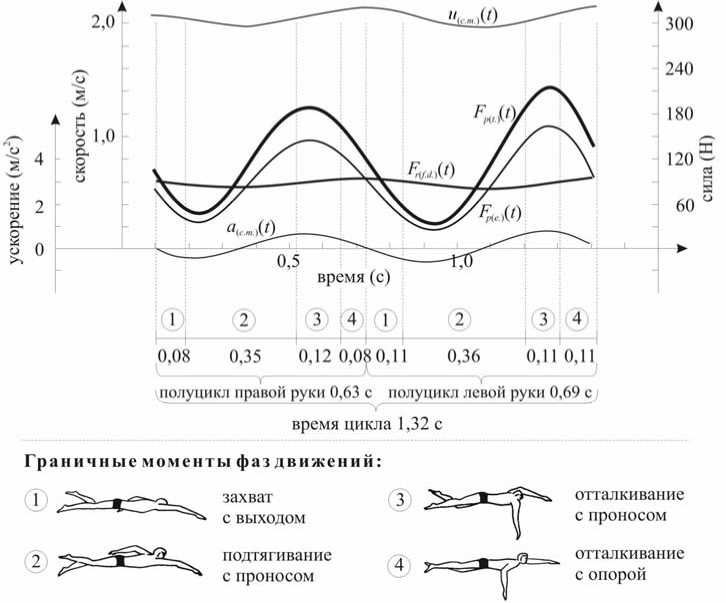
Рис. 2. Кинематические и динамические характеристики цикла движений в плавании стилем кроль на груди испытуемого № 81, победителя Олимпийских игр в Барселоне на спринтерских дистанциях

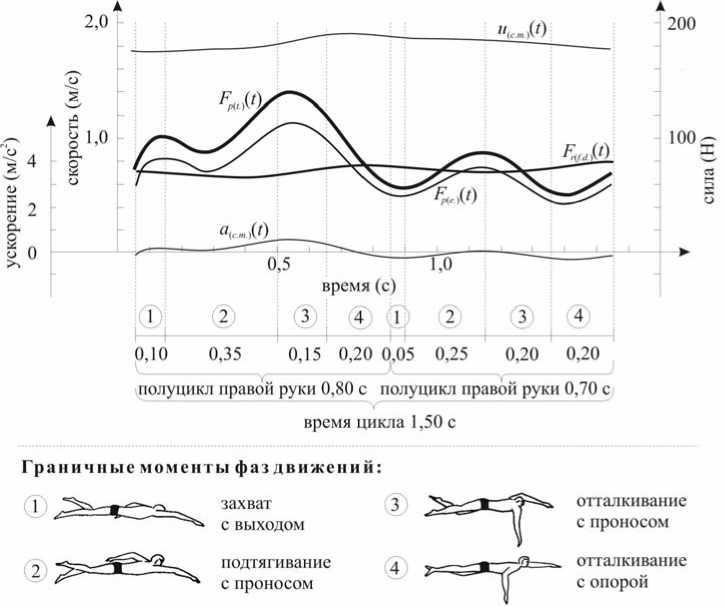
Рис. 3. Кинематические и динамические характеристики цикла движений в плавании стилем кроль на груди испытуемого № 121, победителя Олимпийских игр в Барселоне на средних дистанциях.

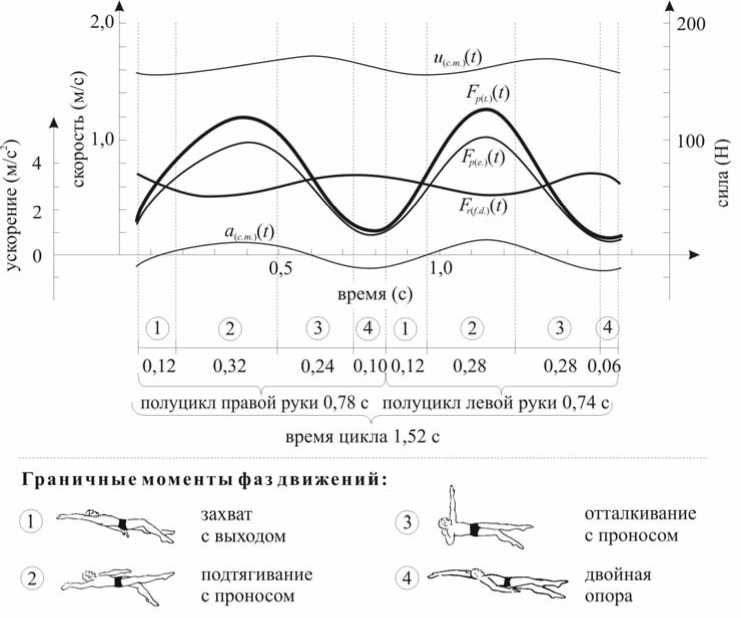
Рис. 4. Кинематические и динамические характеристики цикла движений в плавании стилем кроль на спине испытуемого № 16, победителя чемпионата мира в Риме на дистанции 200 метров

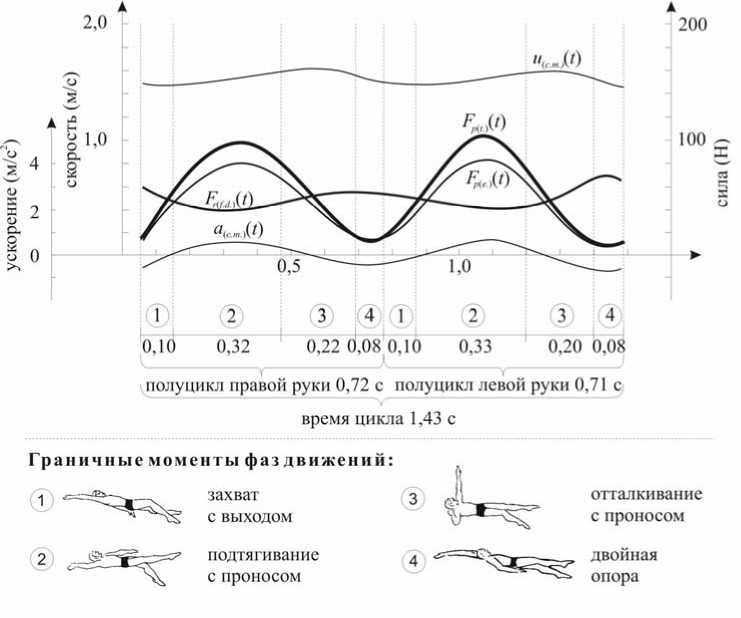
Рис. 5. Кинематические и динамические характеристики цикла движений в плавании стилем кроль на спине испытуемой № 203, призера Олимпийских игр в Атланте на дистанции 100 метров

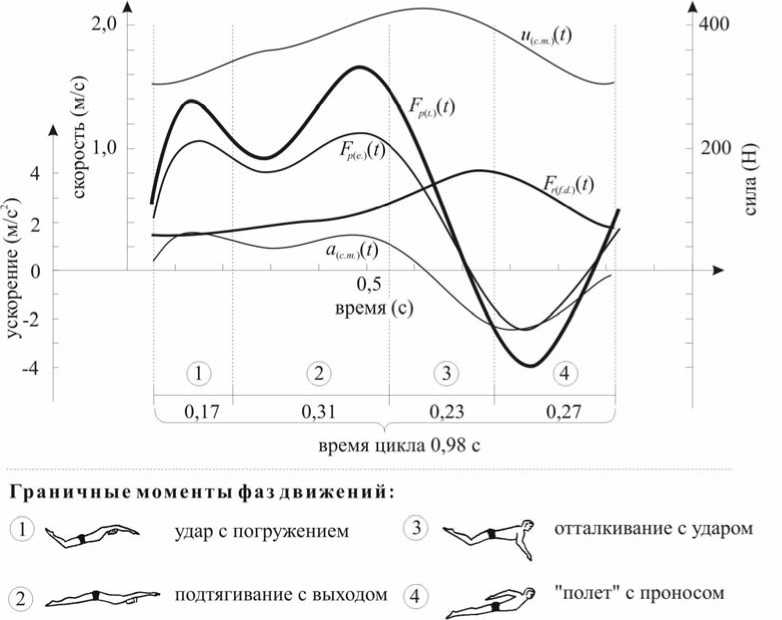
Рис. 6. Кинематические и динамические характеристики цикла движений в плавании стилем дельфин испытуемого № 206, призера Олимпийских игр в Атланте на дистанции 100 метров

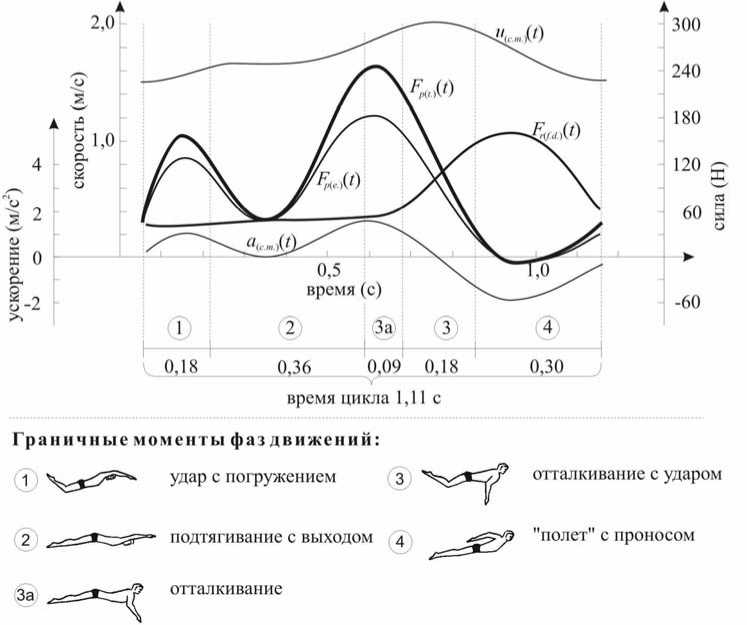
Рис. 7. Кинематические и динамические характеристики цикла движений в плавании стилем дельфин испытуемого № 137, победителя Олимпийских игр в Атланте на дистанциях100 и 200 метров

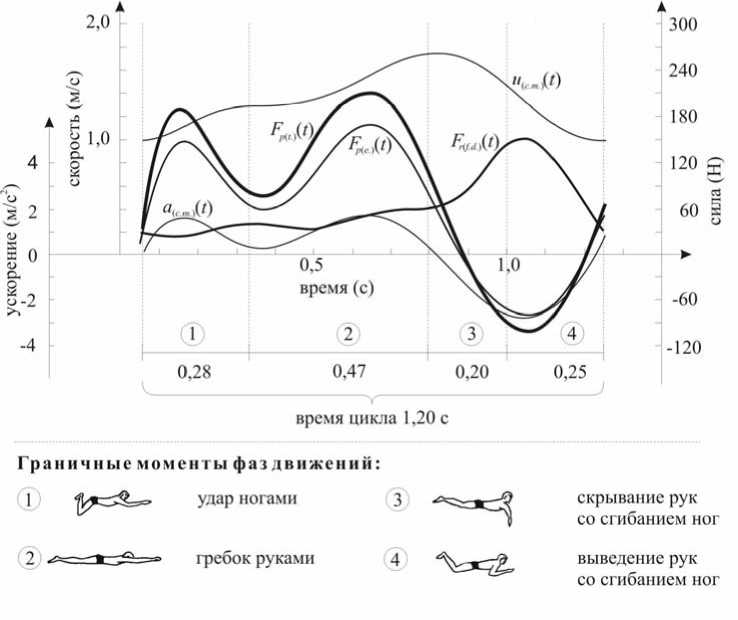
Рис. 8. Кинематические и динамические характеристики цикла движений в плавании стилем брасс испытуемой № 64, победителя Олимпийских игр в Барселоне на дистанции 100 метров

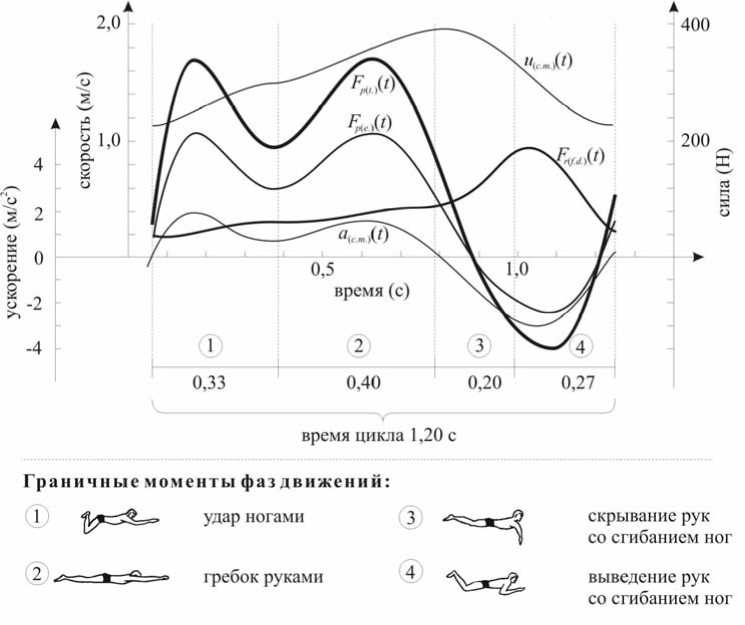
Рис. 9. Кинематические и динамические характеристики цикла движений в плавании стилем брасс испытуемого № 511, финалиста чемпионата мира в Риме на дистанции 100 метров ускорение (м/с2)

сила (Н)

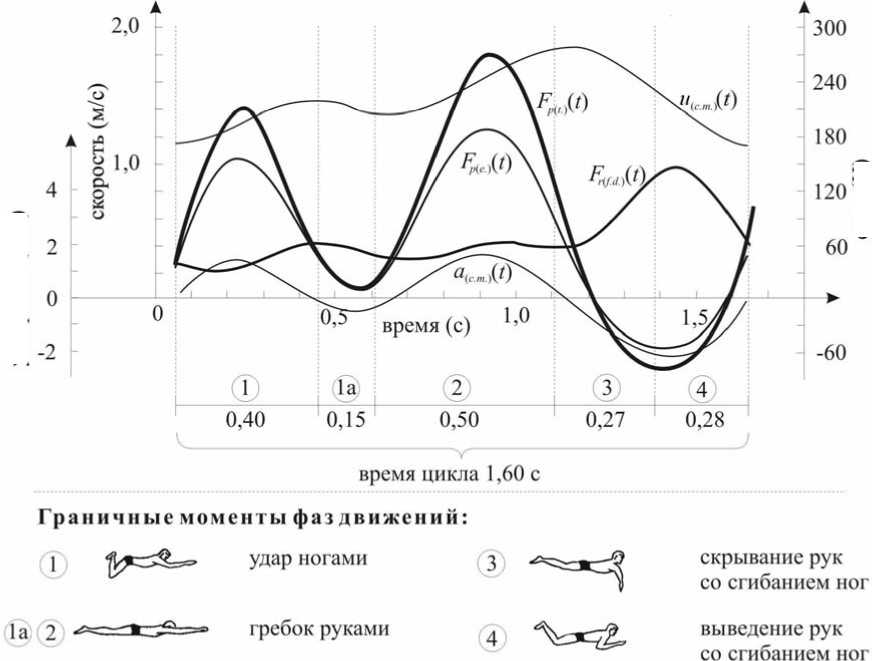
Рис. 10. Кинематические и динамические характеристики цикла движений в плавании стилем брасс испытуемого № 134, финалиста чемпионата мира в Риме на дистанции 200 метров

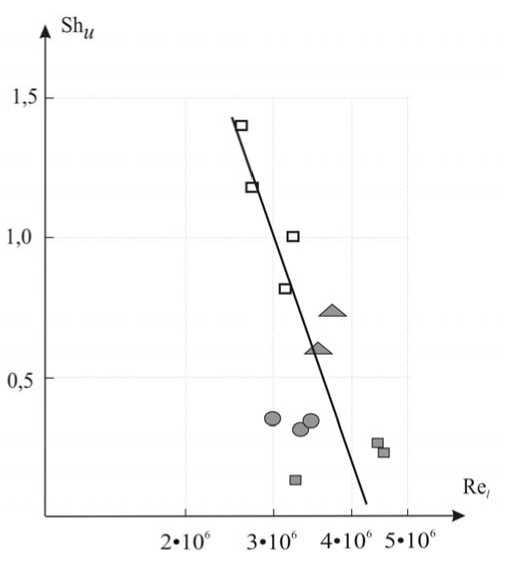
Рис. 11. Итоговая критериальная зависимость между числами Струхаля (Sh u ) и Рейнольдса (Re l ) в различных стилях плавания: ■ - кроль на груди, ▲ - дельфин, • - кроль на спине, □ - брасс

Таблица

Значения экспериментальных показателей основных характеристик биогидродинамического анализа в цикле движений испытуемых

№	Название характеристики	Обозначение	Размерность в СИ	№ 81	№ 121	№ 16	№ 203	№ 206	№ 137	№ 64	№ 511	№ 134
1	Длина тела	L	м	1,97	1,87	1,89	1,78	1,90	1,87	1,75	1,89	1,90
2	Масса тела	m 0	кг	87,00	74,50	74,00	68,00	83,00	79,30	66,20	80,50	76,00
3	Масса жидкости инерционного происхождения	∆ m	кг	8,42	8,40	7,40	7,00	11,29	9,50	8,75	10,70	10,60
4	Критерий Струхаля	Sh u		0,225	0,137	0,335	0,347	0,734	0,599	1,19	1,08	0,801
5	Критерий Рейнольдса (106)	Re l		4,44	3,76	3,38	2,99	3,79	3,55	2,62	3,25	3,10
6	Длина цикла	l ( c. )	м	2,68	2,715	2,45	2,17	1,76	1,90	1,62	1,86	2,35
7	Средняя скорость центра масс тела	u o ( c.m. )	м∙с-1	2,029	1,810	1,611	1,514	1,794	1,710	1,346	1,548	1,471
8	Безразмерный коэффициент силы пассивного сопротивления	C x ( p.d. )		0,274	0,290	0,291	0,320	0,340	0,263	0,288	0,286	0,286
9	Сила пассивного сопротивления	Fr ( p.d. )	Н	110,46	83,88	66,22	59,45	101,14	71,12	43,07	63,57	55,82
10	Характерный гидродинамический размер тела	S 0 ( b.s. )	м2	0,152	0,150	0,154	0,145	0,168	0,153	0,147	0,168	0,160
11	Безразмерный коэффициент силы лобового сопротивления	C x ( f.d. )		0,271	0,288	0,299	0,285	0,354	0,340	0,465	0,430	0,381
12	Сила лобового сопротивления	F r ( f.d. )	Н	75,15	64,64	55,67	43,77	89,71	69,73	59,03	81,49	62,41
13	Безразмерный коэффициент силы активного сопротивления	C x ( а.d. )		0,305	0,306	0,324	0,314	0,450	0,377	0,548	0,631	0,445
14	Сила активного сопротивления	F r ( а.d. )	Н	98,92	77,25	66,33	53,31	125,65	86,99	75,93	130,11	79,80
15	Полезная внешняя механическая мощность	P uo	Вт	152,48	117,00	89,68	66,28	157,89	119,24	79,45	126,15	91,80
16	Тотальная внешняя механическая мощность	P to	Вт	200,71	139,82	106,86	80,71	221,14	148,75	102,20	201,41	117,38
17	Безразмерный коэффициент пропульсивной эффективности	e p		0,760	0,837	0,829	0,821	0,714	0,802	0,777	0,626	0,782

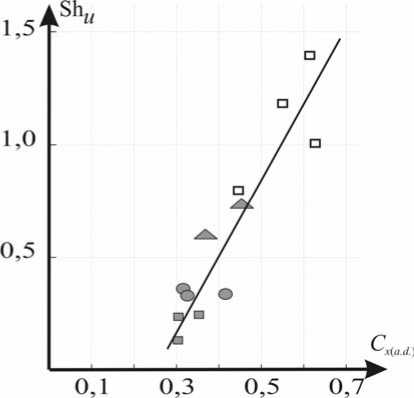
Рис. 12. Итоговая критериальная зависимость между числом Струхаля (Sh u ) и безразмерным коэффициентом гидродинамической силы ( C x(a.d.) ) в различных стилях плавания: ■ – кроль на груди, ▲ – дельфин, • – кроль на спине, □ – брасс

Значения коэфициента пропульсивной эффективности ( e p ) (диапазон колебаний e p от 0,626 до 0,837) сопоставимы с аналогичной характеристикой для волнового и винтового типа движителей [4, 5]. Кроме того, эти значения e p несколько выше значений аналогичного показателя у менее квалифицированных спортсменов [17, 18]. Здесь необходимо отметить, что данные, которые используются для сравнения, получены принципиально другим методом измерения e p ( MAD - system ) [17].

Средние значения гидродинамической силы лобового сопротивления ( F r ( f.d. ) ) в условиях реальных водных локомоций стилями плавания кроль на груди, кроль на спине и дельфин меньше средних значений пассивного гидродинамического сопротивления ( F r ( p.d. ) ) в условиях стационарного движения на аналогичной скорости. Двумя основными причинами этого являются нестационарность движения и уменьшение характерного размера тела в реальных условиях плавания. Кроме того, это обстоятельство исчерпывающе объясняет экспериментальный факт, неоднократно отмечаемый нами ранее, что в стиле плавания брасс имеют место неравенства C x ( a.d. ) >  C x ( p.d. ) , F r ( а.d. ) >  F r ( p.d. ) [3, 9, 12, 13].

Анализ результатов, представленных на рис. 11 и 12, показывает, что наблюдаемое снижение нестационарности плавания спортивными стилями от брасса (Sh u = 1,0–1,5) до кроля на груди (Sh u = 0,1–0,4) сопровождается повышением числа Рейнольдса (Re l ) и снижением безразмерного коэффициента гидродинамической силы ( C x ( a.d. ) ). Следовательно, весьма существенное значение для эффективности плавания человека имеют внутрицикловые колебания скорости, зависящие от биомеханических особенностей различных спортивных стилей. Все это позволяет однозначно говорить о регулирующем значении критерия Струхаля (Sh u ) при установившемся нестационарном плавании человека.