Кинематические соотношения при взаимодействии движителя с грунтом на повороте

Установлены общие кинематические связи при взаимодействии колесного или гусеничного движителя с грунтом в управляемом и неуправляемом повороте. Даны основные теоремы, связывающие положение центров страгива-ния, а также мгновенных центров скольжения опорных площадок колес (гусениц) при стационарном и нестационарном движении с центром поворота машины.

В теории поворота транспортных и тяговых машин задача взаимодействия движителя с опорной поверхностью является одной из важнейших. Сложность изучения силового и кинематического взаимодействия заключается в том, что эти процессы взаимосвязаны и требуют совместного рассмотрения.

Площадка контакта любого элемента движителя при повороте машины, как правило, скользит по основанию. Возникающие при этом в контакте с основанием силы сцепления, подобно силам трения, являются функциями координат мгновенных центров скольжения (С,) (рис. 1, 2), относи тельно которых происходит мгновенно вращательное движение [3, 7, 9, 15]. Для деформируемого грунта силы сцепления характеризуются не только трением поверхностей, но и деформацией грун-

Рис. 2. Схема силового поворота машины с неподвижными колесами

Рис. 1. Схема поворота гусеничной машины

Впервые задача о взаимном расположении центров скольжения при повороте машины сформулирована и решена Ф.А. Опейко. Ему удалось доказать, что центры скольжения прямолинейно-поступательно связанных тел лежат на прямой, перпендикулярной к их относительному сдвигу [9]. Теорема Ф.А. Опейко, получившая широкое применение при исследованиях поворота гусеничных [2, 8] и колесных машин с бортовой (силовой) схемой поворота при неуправляемых колесах [5], позволяет решить задачу определения силовых ( Т_х, Т_у, М ) и кинематических ( R, ю, Vj) характеристик движения.

Однако, математическая теория трения Ф.А Опейко не нашла распространения при описании движения машин с произвольно установленными колесами, ввиду недостаточного количества уравнений связей, накладываемых особенностями расположения колес. Определим эти недостающие связи в случае произвольно расположенных относительно корпуса машины управляемых и неуправляемых колёс.

Рассмотрим движение колеса вращающегося вокруг горизонтальной оси Xj, которая в свою очередь вращается вокруг вертикальной оси Z2, проходящей через центр поворота машины Ос с угловой скоростью со (рис. 3). Плоскостью качения колеса будем называть любую плоскость перпендикулярную оси его вращения. Центральной плоскостью качения - плоскость его симметрии.

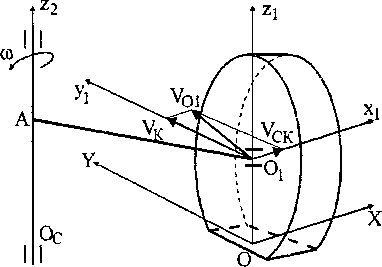
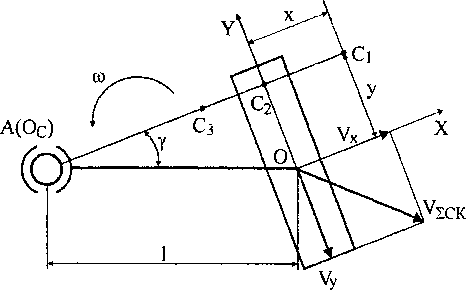
Рис. 3. Схема движения колеса и его опорной площадки по грунту

Свяжем с опорной площадкой контакта местную систему координат ХОУ.

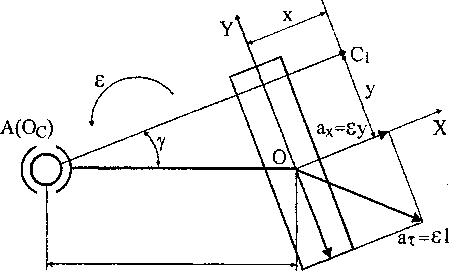
Скорость точки Oj оси вращения колеса равна V_Oi = ©1,где 1 = АО]. Проекция скорости V_Oi на поперечную ось X]равна V_x] = ©lsiny. В боковом направлении колеса справедливо соотношение: V_xl = V_x. Скорость V_x есть ни что иное, как скорость бокового скольжения и равна Vq_K = юу. Следовательно у = 1 sin у.

Этот результат можно сформулировать в виде теоремы, которую в дальнейшем будем называть теоремой ортогональности: при повороте машины центр скольжения опорной площадки произвольно расположенного колеса лежит на перпендикуляре, опущенном из центра поворота машины на плоскость его качения [6,13].

Центр скольжения ведущего колеса располагается правее центральной плоскости качения (Ci), подтормаживающего - левее (С3). Центр скольжения ведомого колеса лежит на пересечении его центральной плоскости качения и перпендикуляра, опущенного из центра поворота машины (С2).

Теорема ортогональности является обобщением теоремы Ф.А. Опейко и позволяет распространить предложенный подход на машины с поворотными колесами, шарнирно - сочлененной рамой и др. [7,13], что значительно расширяет область применения предлагаемой теории поворота.

Теорема ортогональности допускает обобщение и для управляемых колёс.

Пусть корпус машины вращается вокруг оси, проходящей через точку А(ОС) с угловой скоростью ®i, а колесо при управляющем воздействии - относительно оси шкворня, проходящей через точку В, с угловой скоростью ®2 (Рис- 4). При этом ось колеса совершает вращательное движение с угловой скоростью ® = ®1+®2 [12]. Ось суммарного вращения проходит через точку К, распо ложенную на линии АВ и определяемую отрезками АК = Ц ——— и КВ = Ц ———. При вра-©1 +®2 ©1 +®2

щении ©1 и ©2 в разные стороны точка К лежит вне отрезка АВ на продолжении линии соединяющей ось поворота машины и ось шкворня.

Таким образом, мы находимся в условиях действия теоремы ортогональности, где ось Z2 проходит не через точку А, а через точку К . А сама теорема формулируется следующим образом: при повороте машины центр скольжения управляемого колеса лежит на перпендикуляре, опущенном на плоскость его качения из точки К, лежащей на линии, соединяющей центр поворота машины с осью шкворня.

При наличии пары вращений, когда ©2 =-®ь площадка контакта совершает мгновенно поступательное движение [12].

Описанные выше кинематические соотношения системы машина - колесо - площадка контакта являются общими и справедливы для стационарного и нестационарного движения.

Позин Б.М., Трояновская И.П.

Кинематические соотношения при взаимодействии  движителя с грунтом на повороте

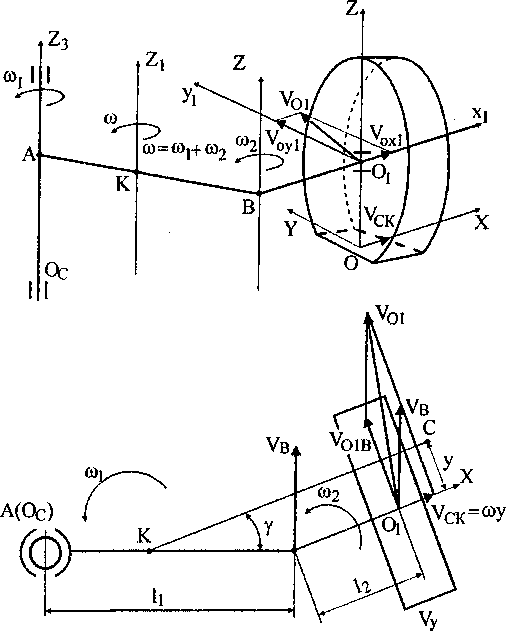
Рис. 4. Схема движения управляемого колеса по опорной площадке

Многие авторы при изучении нестационарного поворота, решая задачи устойчивости и управляемости, ограничиваются, как правило, исследованием различных характеристик в процессе движения, не заостряя внимания на его формировании [4, 11, 14]. Для описания начала движения и построения траектории необходимо задать начальные условия, определяющие решение системы дифференциальных уравнений движения. Начальные условия при этом назначаются обычно исходя из каких-либо общих соображений или из наблюдений за движением экспериментальных объектов без достаточного теоретического обоснования. 1

В качестве начальных условий может выступать решение задачи страгивания, начало изучению которой положил в своих трудах Ф.А. Опейко [3, 9]. Решение задачи страгивания позволяет также определить нагрузки на машину, которые в ряде случаев оказываются наибольшими [1].

■ В момент страгивания, также как и при движении, существуют определенные кинематические соотношения между центрами страгивания машины и опорных площадок контакта колес. Под страгиванием в теории поворота, в отличие от аналогичного понятия при изучении прямолинейного движения, мы будем понимать не только начало движения, но и начало входа в поворот, другими словами - мо мент движения, когда угловая скорость машины о = 0 [1].

В момент страгивания ввиду отсутствия угловой скорости, и как следствие, центров скольжения площадок формально применить доказанные выше теоремы ортогональности не представляется возможным. Однако можно показать, что в начальный момент движения возникающие центры скольжения площадок и поворота машины совпадают с соответствующими центрами страгивания.

На самом деле в момент страгивания (со = 0 ) нормальное ускорение отсутствует (ап = 0 ) и полное ускорение (а ) равно

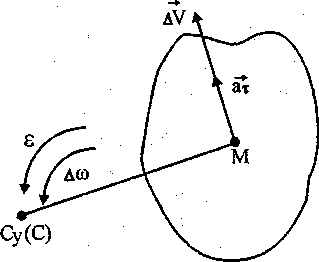
тангенциальному ат=е-СуМ, где Су - мгновенный центр   Рис. 5. К доказательству совпадения центров страгивания и скольжения страгивания площадки (рис. 5), £ - угловое ускорение. Возни-      в начальный момент времени кающее в начальный момент движения малое приращение ско- роста AV любой точки площадки М направлено в сторону ее ускорения ат и равно

AV = CMAo = CM-sAt, где С - мгновенный центр скольжения и поскольку направления ат и

AV совпадают, то совпадают и точки С и Су.

При решении задачи страгивания необходимо определить справедливые для этого момента кинематические соотношения (рис. 6). Опустив доказательства, совпадающие с точностью до терминов с приведенными выше теоремами, можно сказать, что теоремы ортогональности, сформулированные при движении для центров скольжения, справедливы для соответствующих центров страгивания.

Установленные кинематические связи позволяют составить адекватную происходящим процессам математическую модель поворота машины с учетом взаимного расположения и режима движения каждого колеса в отдельности [7,13].

ау=Ех

Рис. 6. Страгивание площадки контакта колеса

Таким образом, независимо от того, поворот какой машины изучается: с колесным или гусеничным движителем, с силовым поворотом или с управляемыми колесами, при движении на твердом или деформируемом грунте, при описании взаимодействия системы машина - колесо - площадка контакта кинематические соотношения являются определяющими и общими. Они основаны на строгих законах механики, что позволяет решать силовую и кинематическую задачи поворота машины совместно.